基于遺傳算法的鋁合金斬波盤等強度優化設計

鮑明森，龔海，張濤，余周香，劉曉龍

(1.中南大學 輕合金研究院，湖南 長沙，410083；2.高性能復雜制造國家重點實驗室，湖南 長沙，410083；3.中國原子能科學研究院 核物理研究所，北京 102413)

高通量反應堆中子源產生的是穩態連續中子束流，為有效截取所需波長的中子，有的中子譜儀使用單色器，也有的譜儀使用中子斬波器(中子飛行時間譜儀)[1-2]。中子斬波器是中子飛行時間譜儀必不可少的關鍵設備，可用于中子波段范圍選擇、脈沖化、單色、周期交疊抑制等[3-4]。轉盤式斬波器是中子斬波器最常用的形式[5]，繞平行于中子束的軸高速旋轉，將連續中子束切割為一系列寬度相等的中子脈沖束(脈沖化功能)[6-8]。隨著對中子飛行時間譜儀性能的要求不斷提高，需要使斬波盤轉速能夠達到20 000 r/min 甚至更高[9-10]，但斬波盤在高速旋轉情況下會產生較大的離心力，當離心力過大時，其內部應力超過屈服強度，發生塑性變形[11]。故對斬波盤進行優化設計是很有必要的。JAFARI 等[12]通過模擬退火和粒子群優化等現代優化方法，以Mises 屈服準則作為約束條件，對變厚度轉盤質量進行了最優設計。KHORSAND等[13]采用混沌粒子群優化方法對轉盤形狀進行優化，從而減小轉盤的應力及位移。曹淼龍等[14]提出了基于STEP/SDAI的轉盤優化設計，合理優化轉盤輪廓線，提高了應力分布均勻性。GUTZWILLER 等[15]利用遺傳算法對渦輪機械盤形狀進行優化，實現了快速低保真度設計。PüHLHOFER 等[10]使用高比強度的CFRP(carbon fiber reinforced plastics)作為斬波盤材料，進行了斬波盤的設計、制造和測試。WEINZIERL等[16]通過數值優化來改進斬波盤，優化槽口形狀，提高斬波盤最大旋轉速度。ANTONELLI 等[17]基于Grammel準則，對變厚度高速旋轉圓盤進行了等強度設計。盡管CFRP是一種輕質堅固的材料，但存在各向異性、加工工藝復雜、經濟成本高等缺點；而鋁合金具有各向同性、易加工、成本低等優點，故本文選擇鋁合金作為斬波盤材料。鋁合金斬波盤存在以下2 個問題：高速旋轉的斬波盤應力較大，易發生變形失效；斬波盤槽口存在應力集中[11]。本文對等厚度和某型號變厚度斬波盤(階梯變化)在20 000 r/min轉速下的工作過程進行有限元仿真，并對二者的應力場進行分析；基于理論計算和遺傳算法，提出一種新的變厚度輪廓曲線，實現連續變厚度轉盤(無槽口)等強度優化設計，減小斬波盤應力，提高應力分布均勻性；通過有限元模擬，對U 形槽口進行局部加厚及增大圓角半徑，有效解決槽口應力集中問題；對優化后的斬波盤在20 000 r/min 及更高轉速下的工作過程進行有限元仿真，研究優化后斬波盤的最高轉速。

1 傳統斬波盤受力分析

1.1 斬波盤介紹

連續波長的中子束通過高速旋轉的斬波盤，被切割為寬度相等的中子脈沖束，使探測器所需波段的中子無損失通過，如圖1所示。斬波盤在高速旋轉過程中會承受極大離心力，若斬波盤材質強度偏低，則工作過程中易變形失效。7050 鋁合金具有密度低、強度高、熱加工性能好等優點，在航空航天結構件上得到廣泛應用[18-19]，因此，本文選擇7050 鋁合金作為斬波盤材料，其材料參數如表1所示。

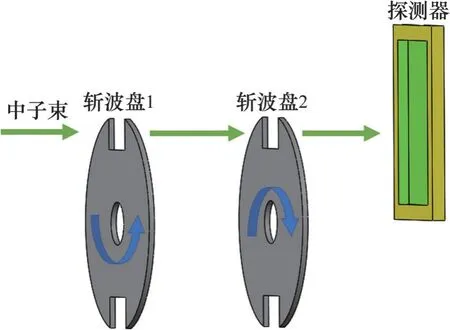
圖1 斬波盤工作示意圖Fig.1 Schematic diagram of chopper disc operation

表1 7050鋁合金材料參數Table 1 Material parameters of 7050 aluminum alloy

斬波盤的典型外徑為500～800 mm，具有不同數量的槽口。本文以某型號斬波盤為基礎，其直徑為700 mm，中心孔半徑為39 mm，共有14 個U形槽口，如圖2所示。

圖2 斬波盤平面圖Fig.2 Floor plan of chopper disc

1.2 等厚度斬波盤受力分析

通過Abaqus 有限元軟件對等厚度斬波盤在20 000 r/min 轉速下的受力情況進行仿真。在仿真過程中，載荷與邊界條件是2個重要因素，其中載荷類型選為“旋轉體力”，角速度為2 095 rad/s；并將中心孔內表面進行完全約束(圖3(a))。

仿真結果如圖3(b)所示。等厚度斬波盤中間部位的Mises應力達到屈服強度，發生塑性變形，因此，以7050 鋁合金為材質的等厚度轉盤無法滿足20 000 r/min的工作要求。

圖3 等厚度斬波盤有限元分析Fig.3 Finite element analysis of chopper disc with equal thickness

1.3 變厚度斬波盤受力分析

針對等厚度轉盤應力過大情況，采用某型號階梯變化的變厚度轉盤，其內圈半徑仍為39 mm，外圈半徑為350 mm，厚度由轉盤的中心到外圈逐漸減小，如表2所示。

根據表2 中數據，對該轉盤在20 000 r/min 轉速下的工作過程進行有限元仿真，結果如圖4 所示。從圖4可見：變厚度轉盤在槽口底部出現應力集中情況，最大Mises應力為455.95 MPa，表明該變厚度轉盤在槽口底部發生塑性變形。為精確分析轉盤的應力分布情況，在轉盤上取如圖4所示的路徑Path-1，其應力變化如圖5所示。從圖5可見：轉盤中心孔Mises 應力較大，為302 MPa；在徑向45～270 mm范圍內，平均應力為252 MPa，應力變化范圍為(252±30) MPa；之后應力逐漸減小，在350 mm處達到最小，為42 MPa。

圖4 變厚度斬波盤Mises應力云圖Fig.4 Mises stress nephogram of chopper disc with variable thickness

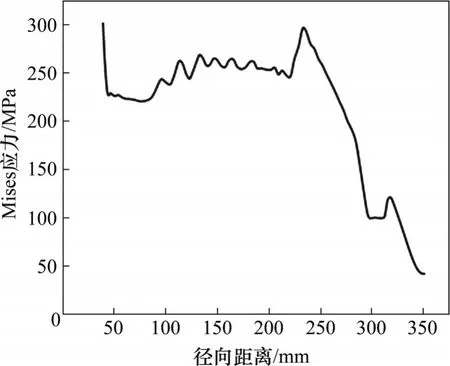
圖5 變厚度斬波盤Mises應力Fig.5 Mises stress of chopper disc with variable thickness

表2 某型號變厚度轉盤參數Table 2 Parameters of a disc with variable thickness

1.4 變厚度斬波盤受力定性分析

呈階梯變化的變厚度斬波盤應力變化趨勢呈鋸齒形波動，且與等厚度斬波盤相比應力明顯減小。

變厚度斬波盤受力定性分析結果如圖6 所示。圖6(a)中，等厚度單元體圓心角為θ，厚度為t，以轉速ω繞中心軸勻速旋轉，質量為m。

式中：ρ為7050 鋁合金密度，t/mm3；R1為外徑，mm；r1為內徑，mm。

等厚度單元體在截面P上的應力為

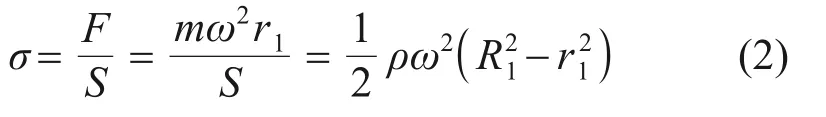
式中：σ為應力，MPa；F為載荷，N；S為截面P的面積，mm2：

由式(2)可知，在同一厚度層內，應力隨徑向距離r1的增大而減小；在階梯位置，厚度變小，使得截面P 的面積減小，引起階梯處應力發生突變，應力變化趨勢由減小轉變為增大。階梯變化的變厚度轉盤在高速旋轉時，出現如圖5所示的鋸齒形波動。

變厚度斬波盤受力定性分析結果如圖6 所示。從圖6(b)可見：當變厚度斬波盤由等厚度轉變為變厚度時，其質量減小至m-m1，即在等厚度的基礎上去除質量為m1的部分。由式(2)可知，當截面積S不變而質量減小時，應力減小。因此，由等厚度轉為變厚度后，截面P上的應力減小。

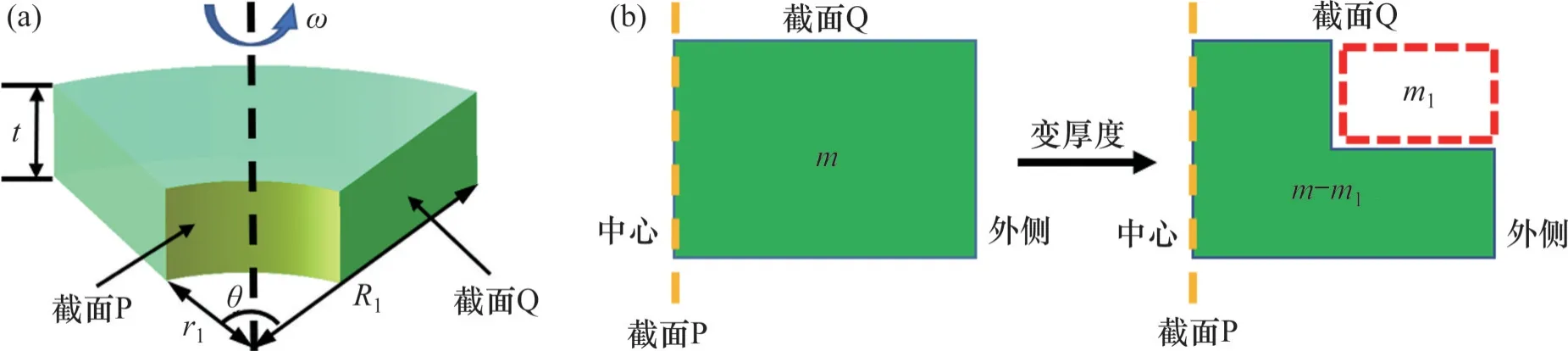
圖6 變厚度斬波盤受力定性分析Fig.6 Qualitative analysis of force of chopper disc with variable thickness

盡管階梯變化的變厚度斬波盤應力相較于等厚度斬波盤應力明顯減小，但仍有不足之處。階梯變化的斬波盤在20 000 r/min 轉速下，整體平均應力及應力變化波動大，中心孔與槽口底部存在應力集中現象。因此，需要通過對斬波盤進行合理的連續變厚度設計，以減小斬波盤應力，提高應力分布均勻性。

2 斬波盤優化設計

2.1 變厚度轉盤形狀優化理論

為優化轉盤的形狀，首先需要推導計算出輪廓曲線為H(r)情況下的徑向應力σr和周向應力σθ，最后計算轉盤的Mises 等效應力σi。通過對輪廓曲線H(r)不斷優化，從而得到最優的變厚度轉盤形狀。

盡管斬波盤外圍存在等間距分布的U形槽口，但這些槽口對斬波盤整體應力影響有限，因此，將其視為規則的變厚度轉盤進行設計。變厚度轉盤示意圖如圖7所示。變厚度轉盤圍繞中心軸作勻速圓周運動，轉速為ω，轉盤內半徑為a，外半徑為b。轉盤在轉動過程中由于離心力的存在會產生內應力，在旋轉體力fr的作用下處于平衡狀態。

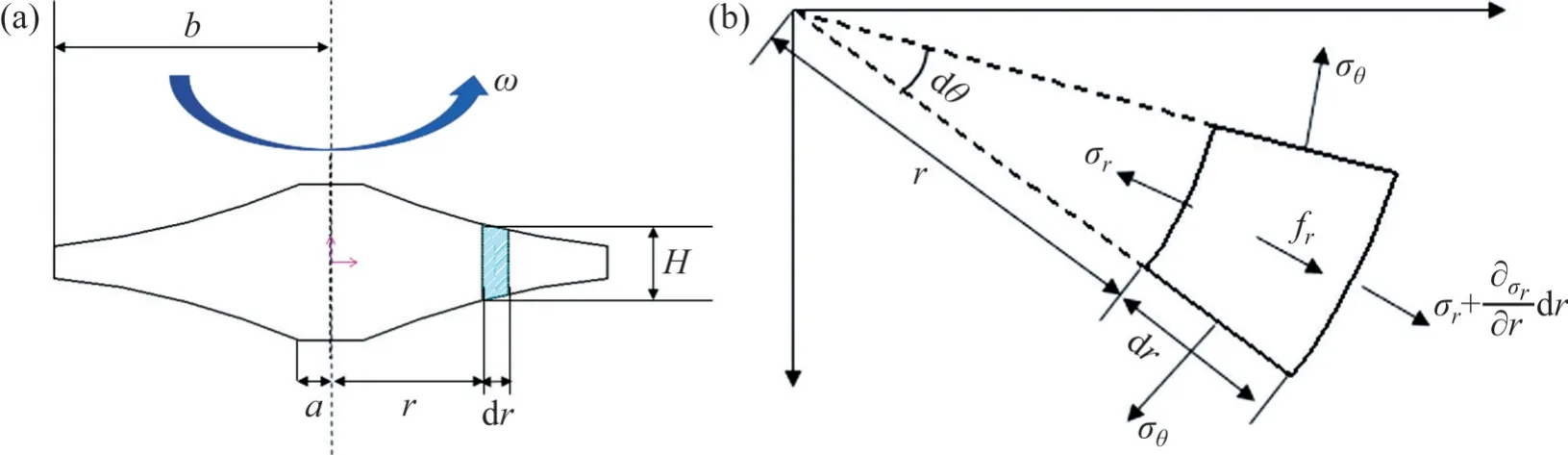
圖7 變厚度轉盤Fig.7 Disc with variable thickness

由彈塑性力學相關理論，可以得到關于位移分量u的微分方程[20-21]：

式中：H為轉盤輪廓曲線函數；u為位移函數；E1為材料彈性模量；μ為泊松比；r為徑向距離(與轉盤中心軸的距離)，mm。該微分方程有以下2個邊界條件：

當輪廓曲線H(r)已知時，通過對微分方程(3)進行求解，得到位移函數u(r)，將求得的位移函數代入式(5)，可求得轉盤的徑向應力σr和環向應力σθ：

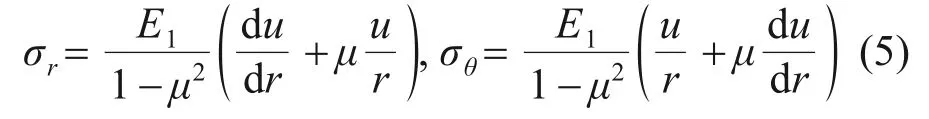
進而求得Mises等效應力 σi：

2.2 基于遺傳算法的變厚度轉盤等強度優化設計

2.2.1 優化參數的選擇

在以往研究中，變厚度轉盤的輪廓曲線一般選擇為雙曲線形式，但在優化過程中發現雙曲線輪廓很難使轉盤達到等強度狀態，為此，本文提出一種新的變厚度輪廓曲線函數，如式(7)所示：

式(7)中右邊前3項是一個標準的二次函數，后2項是指數函數。其中，二次函數項作為轉盤厚度曲線的主體，決定了轉盤厚度的主要變化趨勢，將2個指數項作為微調項分別對轉盤中心和外側的厚度進行局部微調，三者共同作用，可以使轉盤處于理想的等強度狀態。

厚度變化函數H(r)存在5 個未知系數：A，B，C，D和E。其中，A，B，C作為二次函數的3 個系數，對厚度起主要作用。但在用遺傳算法進行優化過程中，如果直接以系數A，B和C為設計變量，則很難得到合適的最優解。變厚度輪廓曲線二次函數項的插值點如圖8所示。對于厚度變化曲線H(r)上i，j和k這3 點的縱坐標，A1，B1和C1為設計變量。通過對i，j和k這3 點進行二次插值計算出系數A，B和C，間接對系數進行優化。

圖8 變厚度轉盤輪廓曲線二次函數項插值點Fig.8 Interpolation points of quadratic function terms of contour curves of variable thickness disc

由于斬波盤中心位置存在1個用于裝夾固定的平臺，因此，厚度變化曲線H(r)從距離中心45 mm處開始(徑向39 mm 至45 mm 范圍內為固定平臺)。點i為曲線起始點，坐標設為(45，A1)；j距離中心軸300 mm，坐標設為(300，B1)；k為厚度變化曲線的終點，坐標設為(350，C1)。通過對A1，B1和C1的取值范圍進行合理的初始化約束，使得它們只能在一個固定區間取值，從而使遺傳算法的搜索范圍受到限制，減小算法的工作量，最終可以快速得到理想的最優解。

其中，第1 個點i的縱坐標A1作為轉盤的初始厚度(轉盤關于X軸上下對稱)，可以根據表2 中變厚度轉盤，給出合理的約束范圍：A1∈(7，15)。第3個點k的縱坐標C1作為邊緣位置厚度，可以根據轉盤的最小厚度對其進行約束。考慮到加工工藝，將轉盤的最小厚度設為1.5 mm。此外，考慮到存在微調項，C1取值范圍可以約束為：C1∈ (-1，1)。第二點j距離中心軸300 mm 處，該位置厚度可以借鑒第3個點k的縱坐標取值，故B1的取值范圍可以約束為：B1∈ (-1，1)。

最后，微調項用于對二次函數進行局部微調整，其取值范圍應控制在較小范圍內，故D和E的取值范圍可以約束為：D∈(-1，1)，E∈ (-1，1)。

2.2.2 參數優化

為合理評估轉盤優化的效果，首先以已有的某型號變厚度轉盤的應力和質量為基準(該轉盤的平均應力為252 MPa、質量為6.8 kg，應力變化范圍為±30 MPa)，對優化后的應力和質量進行量綱一處理，最后對量綱一參數進行加權。

為了減小斬波盤的平均應力，并提高應力分布均勻性，需要同時考慮質量，因此，對應力的權重取為0.8(其中平均應力和應力分布均勻性的權重各取0.4)，而質量的權重取0.2，則設計目標y為

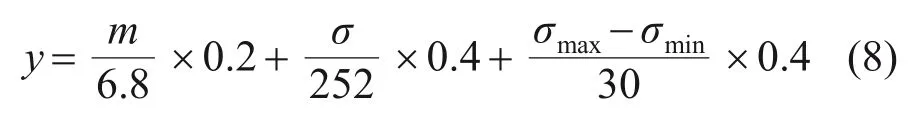
式中：σmax為最大Mises 應力，MPa；σmin為最小Mises 應力，MPa；σmax-σmin用于表征應力分布均勻性；σ為轉盤平均Mises 應力，MPa；m為轉盤的質量。

約束條件為：

1) 轉盤各點的Mises 應力之差不超過15 MPa，轉盤接近等強度狀態，即

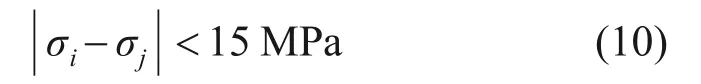
2) 轉盤上各點等效應力Mises 需小于屈服強度，即

式中：σs為材料的屈服強度，MPa。

2.2.3 優化結果

以式(8)的設計目標y作為遺傳算法的適應度，經過不斷優化，得到如下結果：A1=13.443 7，B1=0.123 1，C1=-0.711 4，D=-0.172 5，E=-0.933。

利用二次插值可以計算得到：A=1.165 5×10-4，B=-0.092 4，C=17.367 8。代入式(7)可得輪廓曲線方程：

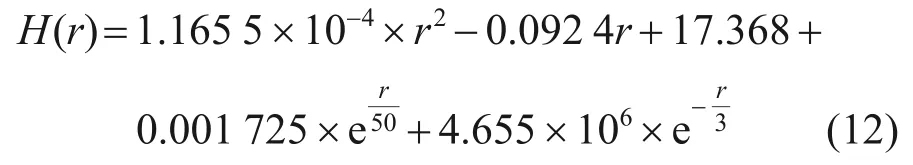
變厚度轉盤輪廓曲線如圖9所示，可見優化后轉盤的厚度變化趨勢為：從中心到外側先減小后增大。由于轉盤關于X軸上下對稱，因此，中心位置最厚為14.87×2 mm，在徑向距離(與轉盤中心軸的距離)315 mm 處厚度達到最小(0.75×2 mm)；接著，厚度逐漸增大，在徑向距離350 mm 處厚度為1.18×2 mm。

圖9 變厚度轉盤輪廓曲線Fig.9 Contour curve of variable thickness disc

通過理論計算，優化后的轉盤在20 000 r/min轉速下的受力情況如圖10所示。從圖10可見：轉盤基本處于等強度狀態，轉盤中心孔位置最大Mises 應力為204 MPa，而轉盤整體平均應力為197 MPa，應力變化范圍為±7 MPa，表明變厚度轉盤的等強度優化設計效果良好。

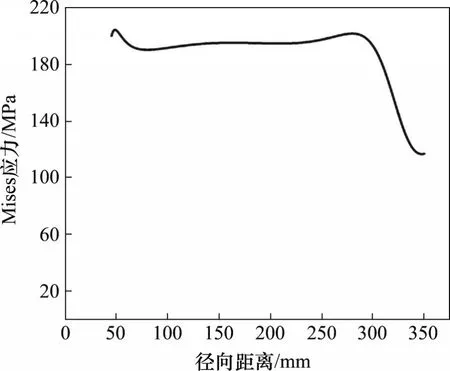
圖10 變厚度轉盤理論計算應力(無槽口)Fig.10 Calculated stress of variable thickness disc(no notch)

2.3 U形槽口局部優化

在等強度優化設計過程中，未考慮斬波盤的槽口。事實上，斬波盤在高速旋轉過程中，槽口底部會出現如圖4所示的應力集中情況，若不對其進行優化，則在工作過程中槽口底部結構將發生破壞。優化槽口的方法有很多，本文采用局部加厚與增大圓角半徑相結合的方式，以減小槽口應力。

2.3.1 局部加厚機理

局部加厚機理分析如圖11 所示。如圖11(a)所示，厚度為h的單元體以轉速ω繞中心軸勻速旋轉，由式(2)可知，當截面積增大，而載荷不變或變化較小時，應力隨之減小。而局部加厚的實質就是通過增加截面積，達到減小槽口處應力集中的效果。

由式(3)和式(5)可知，當轉盤為等厚度盤時，厚度曲線H為常數，因此，等厚度盤的應力與厚度無關。如圖11(b)所示，厚度為h的單元體通過整體加厚和局部加厚2 種方式進行加厚；當采用整體加厚時，單元體呈等厚度狀態，因此，應力不變；而采用局部加厚時，單元體截面積增加，但所受載荷與整體加厚相比有所減小，因此，應力減小。

圖11 局部加厚機理分析Fig.11 Mechanism analysis of local thickening

2.3.2 槽口優化措施

槽口局部厚度優化示意圖如圖12 所示。從圖12(b)可見，M作為起始加厚位置，N作為結束加厚位置，厚度在N處開始減小。在仿真過程中發現，當所加厚度超過5 mm或從所加厚度直接減小至斬波盤原厚度時，N處會出現較大的應力集中，因此，在徑向半徑R為270～285 mm 時，將厚度增至5 mm；為避免厚度減小引起的應力集中現象，徑向半徑R為285～305 mm 時，厚度由5 mm 線性減小至斬波盤原厚度1.6 mm。此外，為進一步降低槽口的應力集中現象，在局部加厚的基礎上適當擴大圓角半徑R至20 mm(如圖12(a)所示)。

圖12 槽口局部厚度優化Fig.12 Optimization of local thickness of notches

2.4 優化后斬波盤受力分析

經過等強度優化、槽口局部優化，分析斬波盤在20 000 r/min 轉速下的受力情況，對其進行有限元仿真，得到如圖13 所示的優化后斬波盤應力分布云圖。從圖13 可見：優化后的斬波盤在槽口底部最大Mises應力為271 MPa，相較于優化前(圖4)，槽口應力減小40.4%。為精確分析優化后斬波盤的應力分布情況，取如圖13 所示的路徑Path-2，得到如圖14所示的應力變化曲線。

圖13 優化后斬波盤Mises應力云圖Fig.13 Mises stress nephogram of the optimized chopper disc

圖14 Mises應力分布Fig.14 Distribution of Mises stress

由圖14 可知：優化后斬波盤中心孔最大應力為200 MPa，在徑向310 mm 之內，平均應力為182 MPa，應力變化范圍為±6 MPa。與理論計算的應力相比，由于槽口存在，影響了斬波盤邊緣應力場，使得斬波盤邊緣應力下降明顯，并使得斬波盤平均應力下降15 MPa，但應力有限元仿真結果仍與理論計算結果相符合，表明設計合理。

3 結果討論

3.1 優化前后應力對比分析

優化前后應力對比如圖15 所示。從圖15 可見：通過優化前后斬波盤應力對比，發現優化后的斬波盤應力顯著減小。優化前斬波盤在中心孔應力為302 MPa，而優化后斬波盤在中心孔應力為200 MPa，中心孔應力減小33.8%；其次，優化前的平均應力為252 MPa，而優化后斬波盤的平均應力為182 MPa，平均應力減小27.8%。

圖15 優化前后應力對比Fig.15 Stress comparison before and after optimization

此外，優化后的斬波盤應力分布均勻性明顯提高。由于優化前的斬波盤厚度呈階梯變化，應力場在階梯位置存在較大波動，使得應力分布均勻性較差。而優化后的斬波盤其厚度連續且合理變化，使得斬波盤的應力變化平緩、分布均勻。由圖15 可知：優化前斬波盤的應力變化范圍為(252±30) MPa，而優化后斬波盤的應力變化范圍為(182±6) MPa，應力分布均勻性提高80%。

3.2 槽口應力與極限轉速

由于U形槽口底部應力高于斬波盤平均應力，因此，斬波盤所能承受的極限轉速主要受槽口應力限制，為探求優化后斬波盤的極限轉速，分別在20 000，24 000，25 000和26 000 r/min這4種轉速下對其進行受力分析，槽口應力分布情況如圖16所示。

從圖16(a)可見：斬波盤在20 000 r/min轉速下槽口最大Mises應力為271 MPa，遠低于屈服強度。由式(2)可知，當轉速提高時，轉盤內應力也隨之增大，且轉盤內應力與轉速的平方呈正比，因此，當轉速提升至24 000 r/min 時，槽口最大Mises 應力為390 MPa(如圖16(b)所示)，此時，安全系數為455/390≈1.17；當轉速提升至25 000 r/min 時，槽口最大Mises 應力為424 MPa(如圖16(c)所示)，此時接近但仍小于屈服強度；當轉速提升至26 000 r/min時，槽口最大Mises 應力為455 MPa(如圖16(d)所示)，此時槽口發生塑性變形。因此，優化后斬波盤極限轉速可達25 000 r/min。

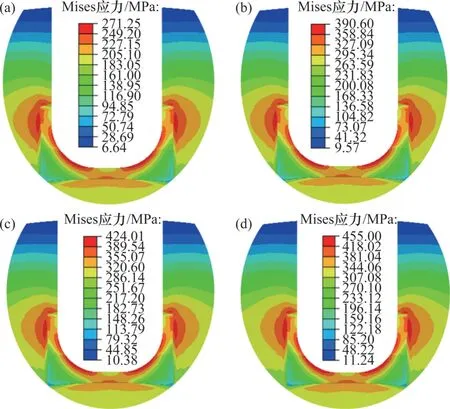
圖16 不同轉速下槽口應力Fig.16 Notch stress at different rotational speeds

3.3 能量分辨率

斬波盤型冷中子飛行時間譜儀通過改變斬波盤旋轉頻率來調整儀器分辨率[22]。通常用入射中子的彈性散射能量峰半寬度ΔEFWHM表征冷中子飛行時間譜儀的能量分辨率，具體表達式為

式中：h為普朗克常數；mn為中子質量；e′為基本電荷；Lsd為樣探距；λi為入射中子波長；λf為散射中子波長；Lpm為第一個斬波盤和最后一個斬波盤的間距；Lms為最后一個斬波盤與樣品之間的間距；ap為脈沖斬波器切口角度；am為單色斬波器切口角度；Ld為飛行距離誤差；vch為斬波盤旋轉頻率。

取λf=λi，忽略小項Cn，則可近似得出

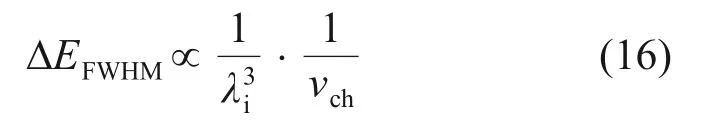
由式(16)可知：當λi不變時，增大斬波盤旋轉頻率vch能有效提高譜儀的能量分辨率。優化前的斬波盤無法滿足20 000 r/min 的工作要求，而經過優化后的7050鋁合金斬波盤在1.17倍安全系數下，最大轉速可提升至24 000 r/min，因此，冷中子飛行時間譜儀的能量分辨率顯著提高，適用于更高頻率的材料微觀動力學測量。

4 結論

1) 針對7050 材質鋁合金斬波盤結構設計不合理、無法滿足高速旋轉的問題，提出了一種連續變厚度輪廓曲線，可實現斬波盤等強度優化設計，并通過局部尺寸優化可大幅度降低斬波盤槽口的應力集中現象。

2) 結構優化后的斬波盤平均應力明顯減小，應力分布均勻性大幅度提高。在20 000 r/min 轉速下，7050 鋁合金斬波盤基本處于等強度狀態，與優化前相比，斬波盤平均應力降低26.7%，應力分布均勻性提高85%。

3) 斬波盤中心孔應力及槽口底部應力大幅度減小。在20 000 r/min 轉速下，與優化前相比，7050鋁合金斬波盤中心孔應力降低33.8%，槽口應力降低40.4%。

4) 斬波盤的最高轉速顯著提升，冷中子飛行時間譜儀的能量分辨率顯著提高，適用于更高頻率的材料微觀動力學測量。在屈服強度為455 MPa、安全系數為1.17 的基本條件下，優化后的7050 鋁合金斬波盤最大許用轉速可達24 000 r/min；當轉速提升至25 000 r/min 時，槽口應力為424 MPa，接近屈服強度；當轉速提升至26 000 r/min 時，槽口應力達到屈服強度，發生塑性變形。