縮尺車輪-環軌試驗臺輪軌靜態接觸相似性研究

羅易飛，趙鑫，周志軍，尹利鈞，溫澤峰，楊吉忠

(1.西南交通大學 牽引動力國家重點實驗室，四川 成都，610031；2.中鐵二院工程集團有限責任公司，四川 成都，610031)

輪軌滾動接觸副具有高速度、高接觸應力及梯度和小應變等顯著特點，并伴有復雜接觸幾何、三向蠕滑、寬頻振動及非線性材料行為等現象，使得輪軌關系問題的研究較為困難。過去幾十年，雖然人們已經在輪軌滾動接觸行為模擬方面取得了較大進展，例如，已被廣泛采用的Kalker 線性理論[1]、集成了沈氏理論[2]的車輛-軌道耦合動力學模型[3]和逐漸發展成熟的輪軌瞬態滾動接觸有限元模型[4-9]，但這些理論方法仍無法完全取代試驗研究。

近年來，NAEIMI等[10]將世界范圍內的輪軌試驗臺按試驗對象歸納為全尺機車車輛-軌輪、全尺車輪-軌輪、全尺車輪-直軌、縮尺雙盤、縮尺輪盤-直軌和縮尺車輪-環軌等六類。按此分類，西南交通大學的機車車輛滾動振動試驗臺[11]屬于全尺機車車輛-軌輪類，最高試驗速度可達600 km/h，主要用于機車車輛的動力學試驗；日本的全尺輪軌試驗臺[12]、中國鐵道科學研究院的高速輪軌關系試驗臺[13-14]屬于全尺車輪-軌輪類，后者最高試驗速度達500 km/h，主要用于輪軌蠕滑、黏著及損傷等的試驗研究；奧鋼聯的輪軌試驗臺[15]、波蘭華沙鐵路研究中心的全尺寸單輪對滾動接觸疲勞試驗臺[16]等屬于全尺車輪-直軌類，車輪或鋼軌往復運動，受限于軌道長度，最高試驗速度在20 km/h以下，且每次循環都存在一個加速—勻速—減速的復雜滾動接觸過程。縮尺雙盤試驗臺因制造和試驗成本低廉而被廣泛采用，代表性試驗臺包括JD-1 型試驗臺[17]、JD-2 型[18]摩擦磨損試驗機、車輪-鋼軌高速滾動接觸疲勞試驗機[19]、波磨模擬試驗臺[20]，其缺點是忽略了輪軌真實幾何尺寸、軌下離散支承等因素，無法精確模擬實際輪軌間的真實接觸狀態。區別于既有成熟的全尺寸滾振試驗臺，縮尺車輪-環軌接觸試驗系統既可獲得較好的試驗結果，還具有高效率、可重復、低成本、多場景應用等多重優勢，是列車實驗技術發展的重要方向，能為列車-軌道復雜場景運行安全的科學評估提供重要技術指導。但目前此類試驗臺在世界范圍內應用仍處于起步階段。為此，荷蘭代爾夫特理工大學(TU Delft)建成了最高速度60 km/h的縮尺車輪-環軌試驗臺[21-22]，將鋼軌離散支撐考慮在內；西南交通大學在高速列車基礎研究平臺建設過程中，建成了考慮鋼軌離散支撐的縮尺車輪-環軌試驗臺，命名為輪軌滾動行為模擬試驗臺[23]，最高試驗線速度為380 km/h，也可實現重載低速模擬。

本文以輪軌滾動行為模擬試驗臺為例，研究縮尺車輪-環軌試驗臺與我國典型高速動車組在輪軌靜態接觸方面的相似性，重點關注不同橫移下的輪軌接觸壓力、接觸斑面積、軌內等效應力分布等，以期為相關試驗研究分析及同類型試驗臺的設計提供參考依據。

1 輪軌滾動行為模擬試驗臺

輪軌滾動行為模擬試驗臺實物、結構示意圖和輪軌截面分別如圖1[23]和圖2 所示。試驗臺主要由高速回轉臺子系統和車輪加載子系統組成；試驗車輪半徑為175 mm，與真實車輪半徑的比例大致為1∶2.63，垂向載荷通過液壓系統施加(液壓動作器最高頻率為30 Hz)；環形試驗軌直徑為3.2 m，通過48組扣件安裝于回轉臺上，軌頭廓形與CN60軌的一致(縮尺比例為1∶3)，對軌腰進行適當加厚以保證其剛度。

圖1 輪軌滾動行為模擬試驗臺[23]Fig.1 High-speed wheel-rail rolling contact behavior test rig[23]

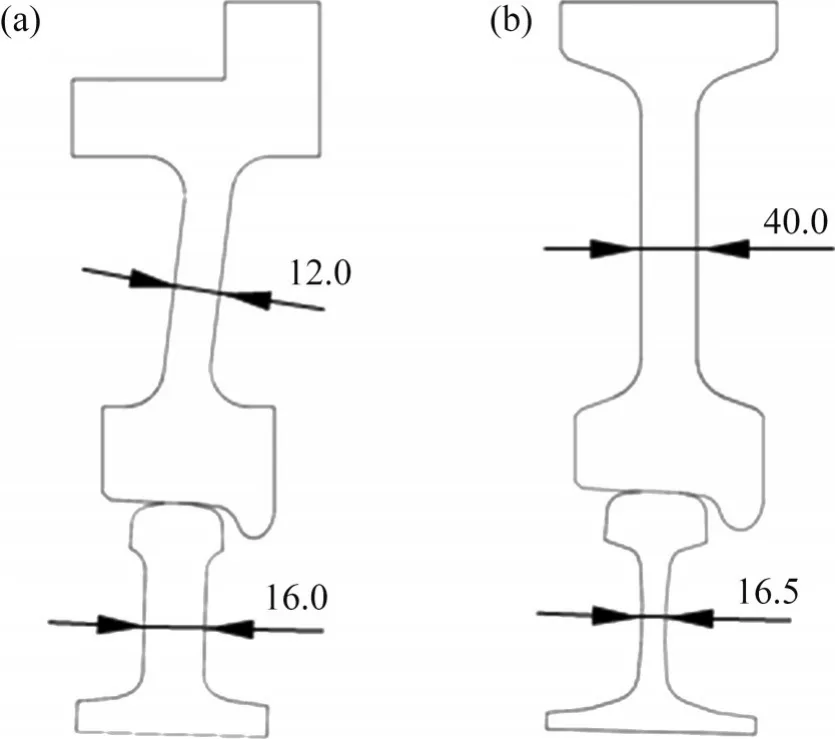
圖2 輪軌截面Fig.2 Wheel and rail sections

TU Delft試驗臺[10]將環軌固定，車輪在其上沿環軌轉動，而輪軌滾動行為模擬試驗臺配備了兩臺獨立的交流變頻電機，分別驅動裝配了環軌的高速回轉臺和車輪，可設定不同的速度差、車輪沖角等參數以實現縱向蠕滑率和橫向蠕滑率的模擬。表1所示為試驗臺主要參數的調節范圍。

表1 試驗臺主要模擬參數的調節范圍Table 1 Adjustment range of main simulation parameters of test rig

該試驗臺具有以下優點：1) 線速度最大值為380 km/h，同時具備重載試驗能力；2) 考慮了鋼軌離散支承及軌下結構的彈性和阻尼特性，可將鋼軌彎曲應力考慮在內。試驗臺輪軌系統與實際輪軌間的差異如下：1) 輪軌截面與真實輪軌不是簡單的縮放關系，輪轂、輪輻和軌腰、軌底幾何存在一些差異；2) 軌道半徑很小，與現場差異明顯；3) 車軸承載位置與現場不同；4) 試驗車輪不能模擬現實中存在的側滾角，其值始終為0。該試驗臺的設計初衷是對鋼軌均勻磨損、波浪形磨損等磨耗問題以及壓潰、龜裂、剝離、斜裂紋等輪軌滾動接觸疲勞問題進行試驗研究。

2 輪軌靜態接觸有限元模型

2.1 試驗臺

利用Abaqus 建立如圖3 所示的試驗臺輪軌接觸有限元模型，包括車輪、車軸、鋼軌、扣件系統、回轉臺基座。本文僅考慮一段弧長0.628 m的試驗鋼軌，包含3 組間距為209.44 mm 的扣件系統，車輪處于中間扣件的正上方，軌道曲線半徑和車輪直徑分別取1.6 m 和350 mm。車輪零橫移位置對應著輪背和鋼軌軌距標記點橫向間距為13.67 mm 的接觸狀態(現場橫向間距對應值為41 mm)。為方便描述，建立坐標原點位于鋼軌頂面中心的笛卡爾坐標系Oxyz，y軸方向為橫向且與零沖角條件下的車輪軸線平行，其正向背對輪緣。

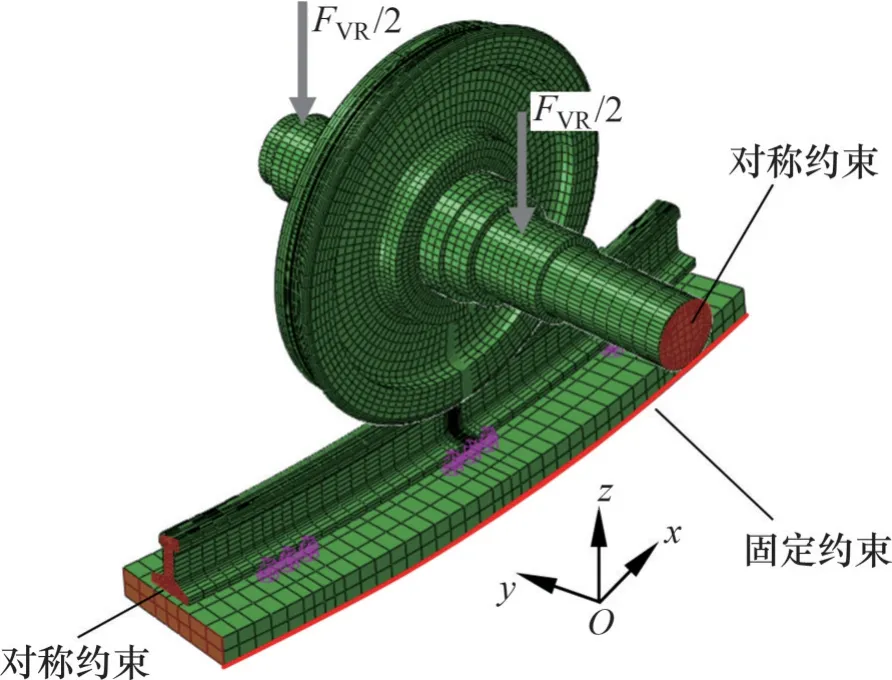
圖3 試驗臺輪軌接觸有限元分析模型Fig.3 Finite element model of test rig for wheel-rail contact analysis

模型中鋼軌廓形與CN60的一致，車輪廓形與LMA磨耗型踏面的一致，縮尺比例均為1∶3，軌底坡坡度取1∶40，縮尺比例為1∶1，輪軌取與服役輪軌相同的材料參數。為獲取足夠的接觸計算精度，同時盡量降低模型規模，采用不均勻的8節點六面體單元(C3D8R)網格離散輪軌模型，接觸求解區內網格邊長取0.33 mm，其他區域網格邊長取值較大，最大網格邊長為21.8 mm。每組鋼軌扣件由12個分布在扣件支撐面內的彈簧單元組模擬，僅保留垂向自由度。最終，模型總節點和單元數分別為134 829 和118 564 個。類似模型的可靠性已得到廣泛證明[24-25]。

由于車軸以上的懸掛結構的剛度、阻尼特性對輪軌靜態接觸幾乎無影響，通過兩側車軸承載部分的表面耦合參考點施加車輪所受垂向載荷FVR[19-20]，參考點僅保留垂向自由度。同時，對整個模型施加重力載荷。輪軌接觸采用基于罰函數的“面—面”接觸算法求解，摩擦因數取開放環境下的典型值0.3。更多邊界條件設置如下：回轉臺基座及鋼軌在車輪滾動方向的兩端面設置對稱邊界條件；回轉臺基座底面固定約束；車軸輪緣一側端面(通過萬向軸與驅動系統連接)施加對稱約束，限制車輪橫向運動。模型僅限于靜態分析，故忽略系統中所有的阻尼特性。模型參數見表2。

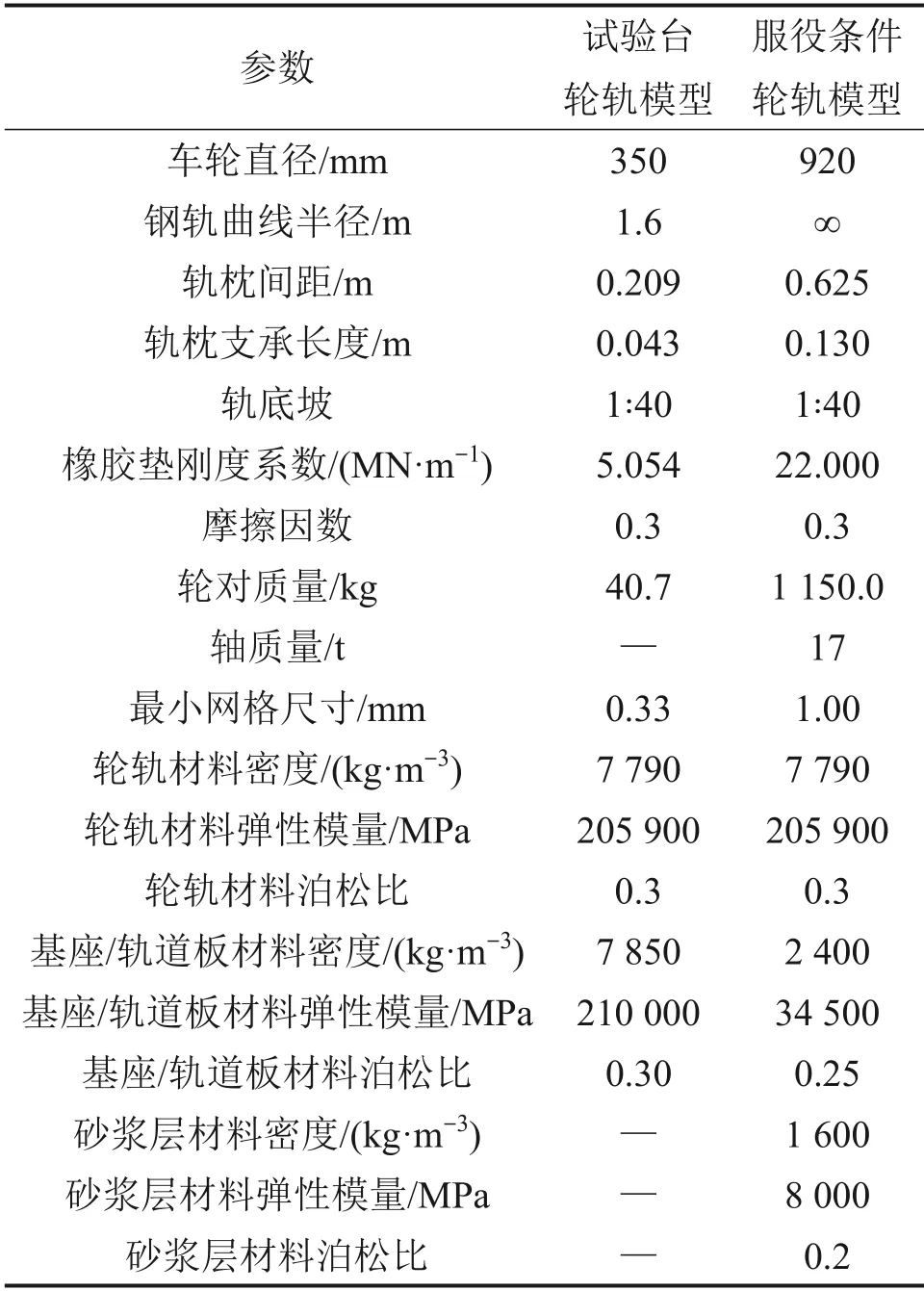
表2 試驗臺與服役輪軌模型參數Table 2 Model parameters of test rig and in-service wheel-rail

2.2 服役輪軌

同樣利用Abaqus 建立如圖4 所示的現場服役輪軌接觸有限元模型。該模型包含單輪對、鋼軌、扣件系統、軌道板、CA 砂漿層等，輪對取自CR400AF 中國標準動車組，軌道參數取自我國某時速350 km級高速鐵路，具體參數見表2。該模型可以準確模擬現場運行中輪對的側滾、搖頭和橫移等輪軌接觸狀態。因高速鐵路正線軌道曲線半徑很大，所以模型中考慮了包含3 組扣件(間距為625 mm)的直線軌道，車輪處于中間扣件的正上方。為方便展示結果，建立坐標原點位于左軌軌頂中心的笛卡爾坐標系Oxyz，向左的輪對橫移定義為正，輪對搖頭角的正方向以右手法則確定。

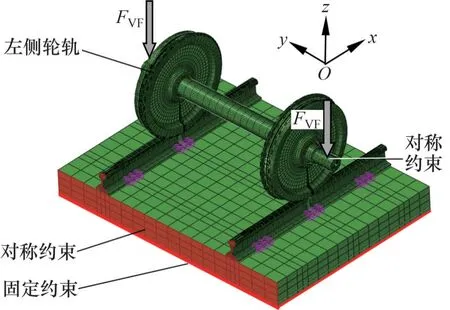
圖4 服役輪軌接觸有限元分析模型Fig.4 Finite element model of in-service wheel-rail for contact analysis

鋼軌和車輪廓形分別為CN60 和LMA 磨耗型踏面廓形，軌底坡坡度取1∶40，輪軌材料參數與試驗臺輪軌參數相同。基于不均勻網格劃分策略，采用C3D8R 單元離散輪軌，接觸求解區網格邊長為1 mm，與試驗臺最小網格邊長的比值為3∶1，模型總節點和單元數分別為323 412 和288 960 個。接觸算法、扣件系統模擬和其他建模細節均與試驗臺模型一致。車輪所受載荷通過參考點的方式施加，施加位置位于兩輪外側(與現場一致)，對整個模型施加重力。更多邊界條件設置如下：軌道在車輪滾動方向的兩個端面(包括鋼軌)的約束均為對稱約束，CA砂漿層底面為固定約束。

3 接觸結果對比

3.1 試驗臺垂向載荷確定

為模擬輪軌現場服役狀態，一般保證試驗載荷下縮尺輪軌間最大接觸應力與現場一致。在Hertz型接觸前提下，若最大接觸應力相同，則試驗臺與現場的垂向總力(法向接觸應力在接觸斑內的積分)之比等于兩種條件下的接觸斑面積之比。針對輪軌滾動行為試驗臺，試驗車輪(直徑為350 mm)與我國復興號標準動車組車輪(直徑為920 mm)的輪徑比為1∶2.63，在試驗臺輪軌廓形與現場廓形縮尺比例為1∶3的前提下，試驗臺與現場垂向載荷之比(φFN)約為1∶7.89。

根據高速動車組服役條件，在服役輪軌有限元模型中施加了17 t軸重。試驗臺模型中對車輪施加的對應垂向載荷FVR應為10.56 kN，具體由式(1)算得：

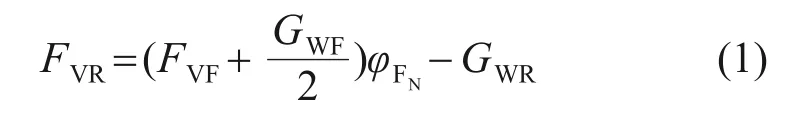
式中：FVF為服役車輪單側懸掛處的垂向載荷，取77.26 kN；GWR和GWF分別為試驗車輪和服役輪對的自重，取0.40 kN和1.15 kN。

為使試驗輪軌接觸壓力水平與服役條件更接近，還需采用試錯法對上述初步計算得到的載荷進行調整。假設車輪位于軌枕正上方，當試驗臺垂向載荷在8.86～12.58 kN 范圍內變化時，輪對零沖角和零橫移條件下的接觸斑內最大壓力和鋼軌內最大Von Mises等效應力結果如圖5所示。可見，在所考慮的垂向載荷范圍內，最大接觸壓力和軌內最大Von Mises 等效應力均隨垂向載荷單調增加，近似呈線性相關。由服役模型計算得到的相應最大接觸壓力和軌內最大Von Mises 等效應力分別為1 114.93 MPa和636.82 MPa，由此可知當試驗臺FVR為10.56 kN 和9.34 kN 時，其輪軌間最大接觸壓力和軌內最大Von Mises 等效應力分別與服役輪軌的一致。這說明，追求最大接觸壓力和最大軌內Von Mises 等效應力一致所對應的試驗臺垂向載荷具有不可忽略的差異(相對誤差約11.6%)。如前所述，本文采用最大接觸壓力模擬準則，故下文計算均取FVR=10.56 kN，對應的包括車輪自重在內的總垂向載荷為10.96 kN。

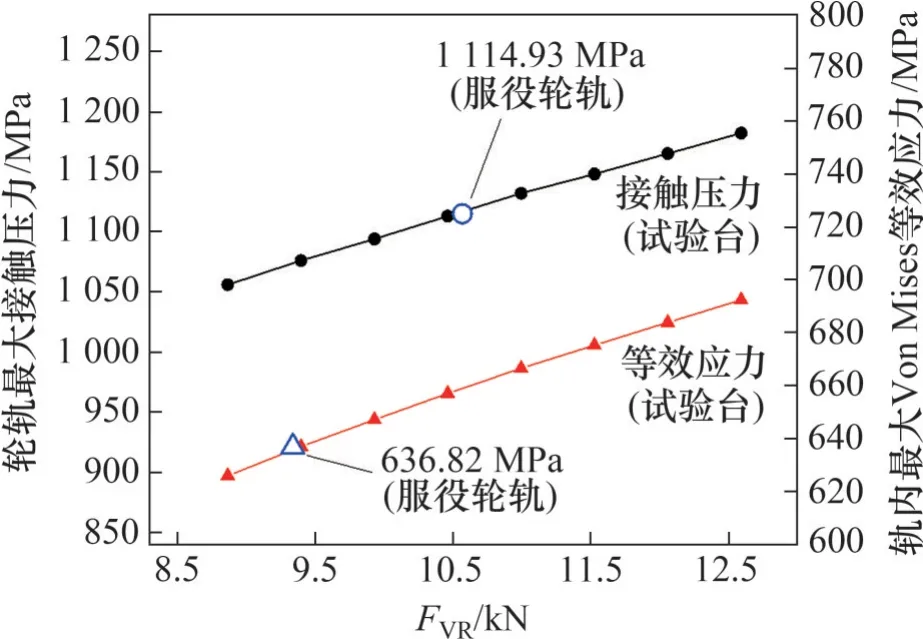
圖5 最大輪軌接觸壓力和軌內最大Von Mises等效應力隨FVR的變化Fig.5 Variation of the maximum wheel-rail contact pressure and the maximum Von Mises equivalent stress in rail with FVR

3.2 接觸斑及接觸壓力分布

選用3.1節中的垂向載荷條件，利用試驗臺和服役輪軌有限元模型分別得到車輪位于軌枕正上方及無沖角和橫移條件下的輪軌接觸斑及接觸壓力分布云圖，如圖6所示。可見，試驗臺和服役輪軌模型得到的最大接觸壓力分別為1 116.97 MPa和1 114.93 MPa，相對誤差僅0.18%。兩個接觸斑在形狀上相似，均近似由兩個短半軸不同的半橢圓“拼合”而成。試驗臺和服役輪軌的接觸斑面積分別為16.12 和119.87 mm2，前者乘以7.89 的縮放比(下文圖中數據皆作類似處理)之后與后者的相對誤差為6.10%。

圖6 比例載荷作用下的接觸斑Fig.6 Contact patch of test rig and in-service wheel-rail under proportional load

圖7所示為車輪位于軌枕正上方和兩軌枕正中時的接觸斑內節點分布。為方便對比，將坐標平移或轉動，使接觸斑中心處于坐標原點處。可見，無論是試驗臺模型還是服役輪軌模型，車輪位于軌枕正上方或兩軌枕跨中時的接觸斑都基本重合，接觸斑面積相對誤差分別為1.40%和0.85%，均由接觸斑邊緣低應力節點的變化所致。另外，試驗臺模型預測的最大接觸壓力在軌枕正上方和跨中時分別為1 116.97 MPa 和1 112.43 MPa，變化幅度為0.41%；服役輪軌模型的對應結果分別為1 114.93 MPa 和1 109.77 MPa，變化幅度為0.46%，二者的變化趨勢一致。

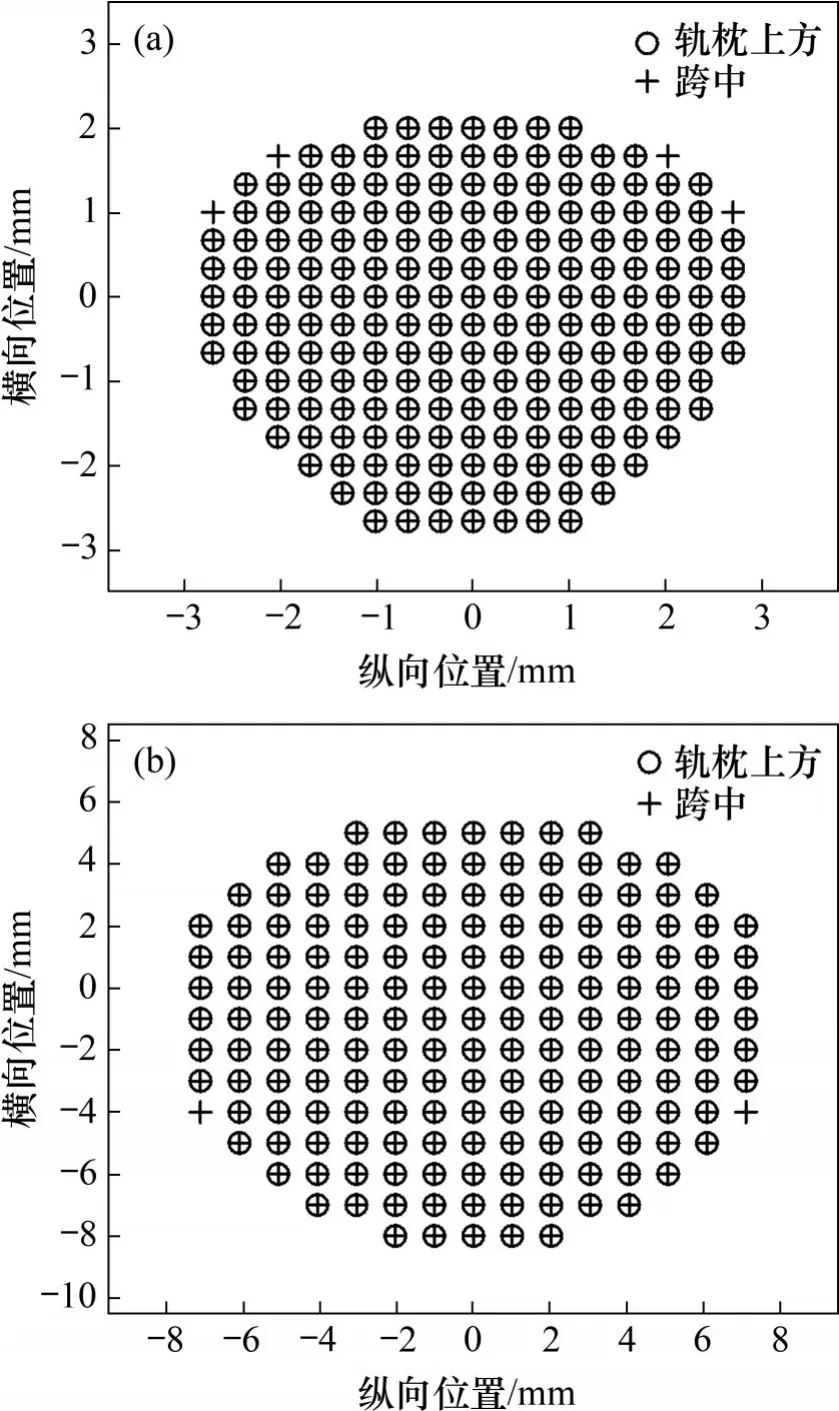
圖7 車輪位于軌枕正上方和兩軌枕正中時的接觸斑內節點分布Fig.7 Node distribution of in contact patch of test rig and in-service wheel-rail when the wheel is located above the sleeper and in the middle of the two sleepers

3.3 沖角、橫移及側滾的影響

保持零橫移不變，使輪對沖角在0°～0.3°范圍內變化(高速動車組在正線上運行時輪對沖角很小)，得到最大接觸壓力和接觸斑面積隨沖角的變化如圖8所示。經計算，試驗臺和服役輪軌的最大接觸壓力均保持在1 116.97 MPa和1 114.93 MPa左右，變化幅度分別小于等于0.32%和0.07%。圖9所示為當試驗車輪沖角分別為0°和0.3°時接觸斑內節點分布的變化。結合圖8可見，沖角僅會使接觸斑在鋼軌上的位置超前或滯后，其形狀和面積基本上無變化。服役模擬的分析結果也得到相同的結論。所以，后續分析中忽略沖角的影響。

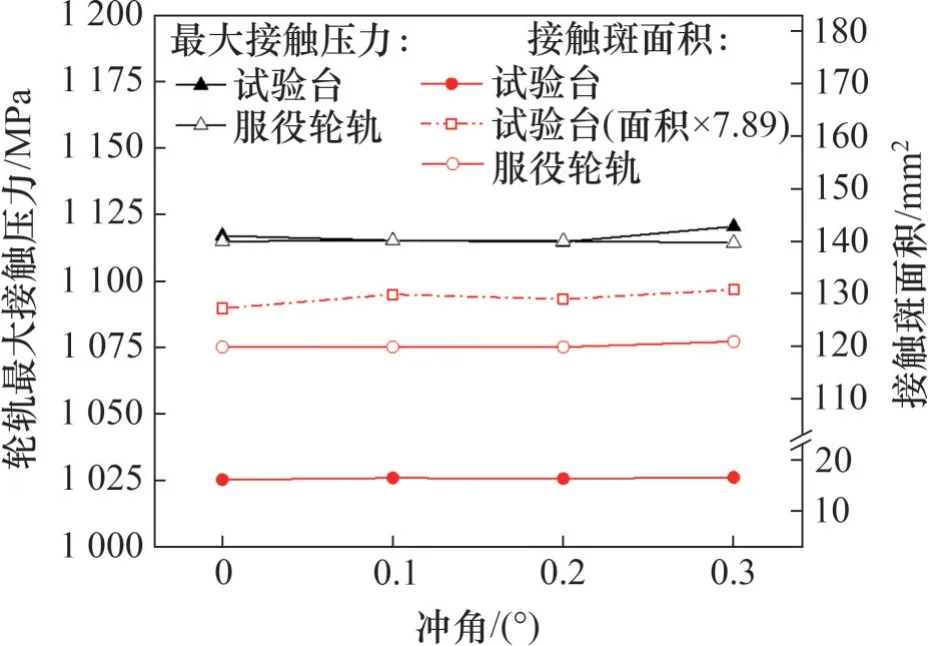
圖8 不同沖角下試驗輪軌最大接觸壓力和接觸斑面積Fig.8 The maximum contact pressure and contact patch area of test rig at different wheel-rail impact angles

圖9 試驗輪軌接觸斑形狀隨沖角的變化Fig.9 Shape variation of rig's wheel-rail contact patch with attack angle

保持零沖角不變，改變輪對橫移及相應側滾角，得到的分析結果對比見圖10。由圖10 可見：當試驗臺車輪橫移為負或小于1.0 mm(對應服役輪對橫移小于3.0 mm)時，試驗臺與服役輪軌最大接觸壓力的相對誤差在5.2%以下。當正向橫移繼續增加時，試驗臺的最大接觸壓力明顯比服役輪軌的高。例如，當試驗臺橫移1.33 mm和服役輪軌相應橫移4.00 mm時的輪軌最大接觸壓力相對誤差達17.92%；而當試驗臺和服役輪軌分別橫移3.0 mm和9.0 mm 時的輪軌最大接觸壓力相對誤差進一步增至123.22%。需要說明的是，對于直線軌道而言，由于左右側對稱，故圖10 僅展示服役輪軌預測模型中左側輪軌接觸結果。

圖10 輪軌最大接觸壓力隨橫移的變化Fig.10 Variation of the maximum wheel-rail contact pressure with lateral displacement

圖11 所示為接觸斑面積隨橫移的變化，其中包含了試驗臺模型的原始預測結果和按比例放大(橫移按1∶3、面積按1∶7.89 的比例放大)后的結果。當試驗臺橫移為負時，模型預測的接觸斑面積比服役輪軌的高約15.22%，但接觸斑面積隨橫移的變化趨勢和服役輪軌的一致。當試驗臺車輪正向橫移超過1.0 mm 時，模型預測的試驗輪軌接觸斑面積偏小，且與服役輪軌的相對誤差進一步增大。例如，試驗臺橫移為2.67 mm和服役輪軌對應橫移8.0 mm時的接觸斑面積相對誤差達39.36%。

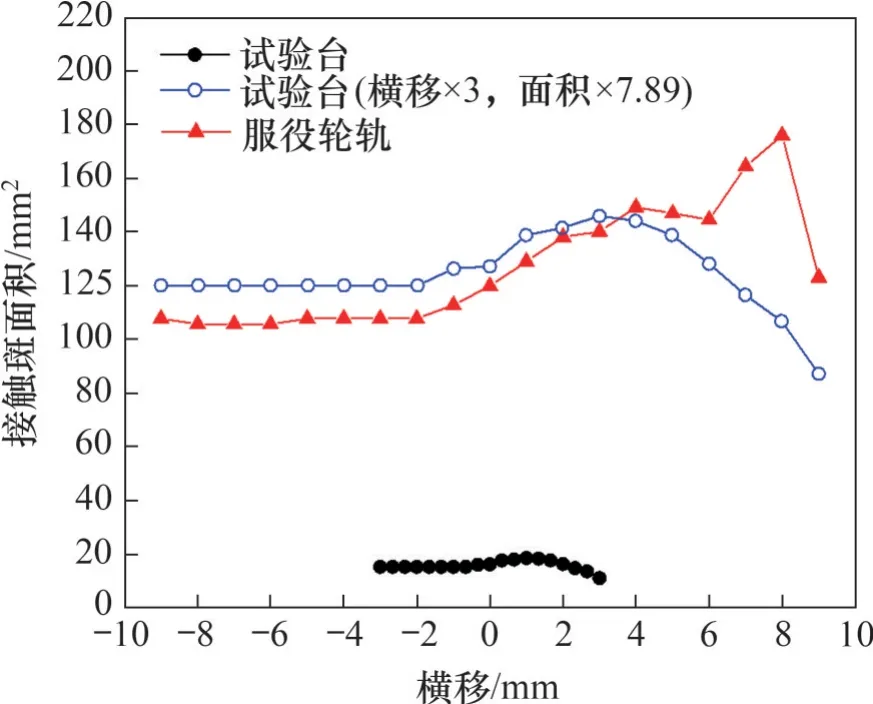
圖11 接觸斑面積隨橫移的變化Fig.11 Variation of contact patch area with lateral displacement

圖12 所示為試驗車輪橫移分別為1.0，2.0 和3.0 mm 以及服役輪對橫移分別為3.0，6.0 和9.0 mm 時的接觸斑。圖中標注了附于鋼軌的坐標系，以便觀察接觸斑在鋼軌頂面上的位置變化。當橫移量為1.0(3.0) mm 時，試驗臺與服役輪軌在接觸斑在形狀上已出現了明顯的區別。當試驗臺車輪橫移為3.0 mm 時，接觸斑較為狹長，但未發生輪緣貼靠，最大接觸壓力高達2 534.73 MPa，遠大于服役輪對相應橫移9.0 mm 時的最大接觸壓力1 135.55 MPa。

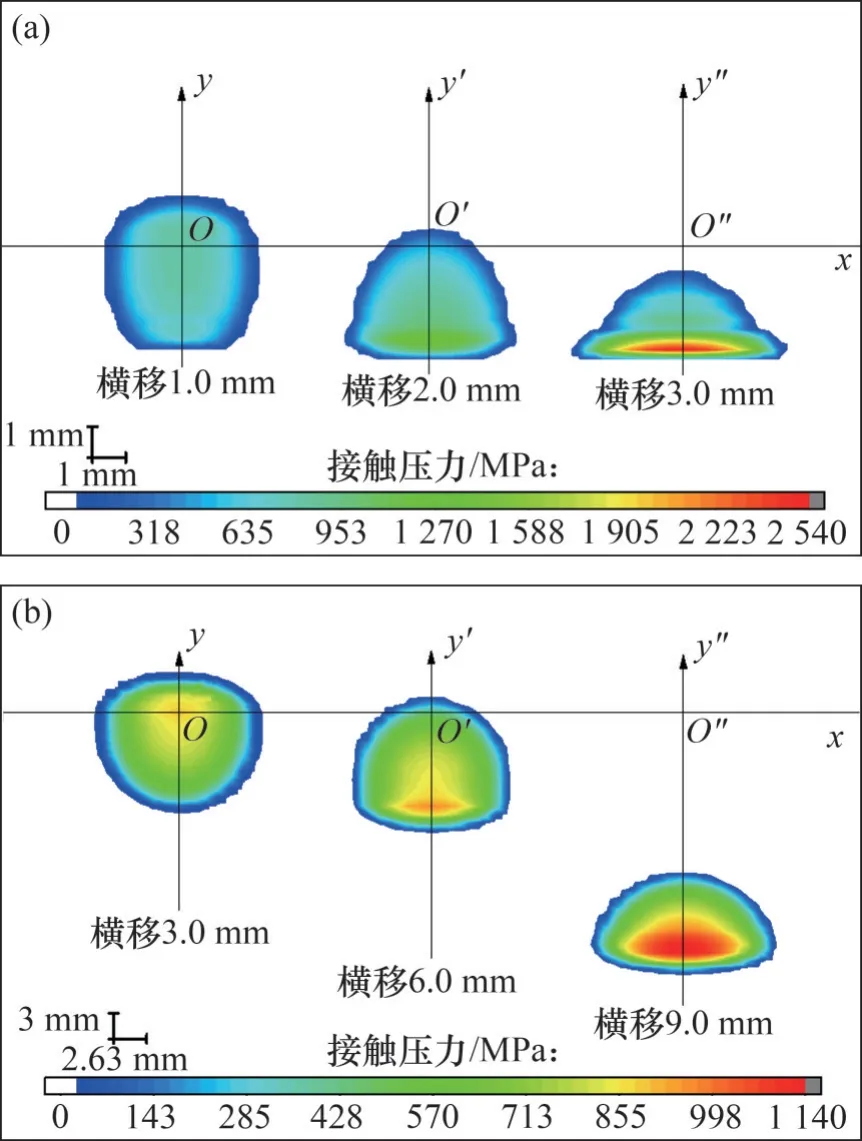
圖12 正向橫移時試驗臺和服役輪軌的接觸斑Fig.12 Contact patches of test rig and in-service wheelrail in the case of positive lateral displacement

造成上述誤差的原因是試驗臺忽略了側滾角。圖13 所示為試驗臺和現場輪軌的剛性接觸點對，其中試驗車輪橫移為-4.0～4.0 mm，服役輪對橫移為-12.0～12.0 mm。其中，服役輪軌結果采用全輪對計算，考慮了輪對側滾的影響，而試驗臺使用單輪模型計算，忽略了側滾的影響。由圖13可見，當試驗車輪負向橫移時，輪軌接觸點在鋼軌上的位置始終位于軌頂中心；當負向或正向橫移超過3.0 mm 時，由于側滾自由度的不同，二者接觸點位置存在明顯差異。

圖13 試驗臺和服役輪軌的接觸點對Fig.13 Wheel-rail ontact points of the test rig and inservice wheel-rail

圖14 所示為服役輪軌側滾角隨橫移的變化。可見，服役輪對側滾角(絕對值)隨橫移(絕對值)的增大而單調上升，并在橫移絕對值大于10.0 mm時，側滾角絕對值開始陡然上升。具體而言，當輪對橫移為-9.0～9.0 mm 時，服役輪軌側滾角取-0.028°～0.028°；相對地，試驗車輪側滾角始終為零。

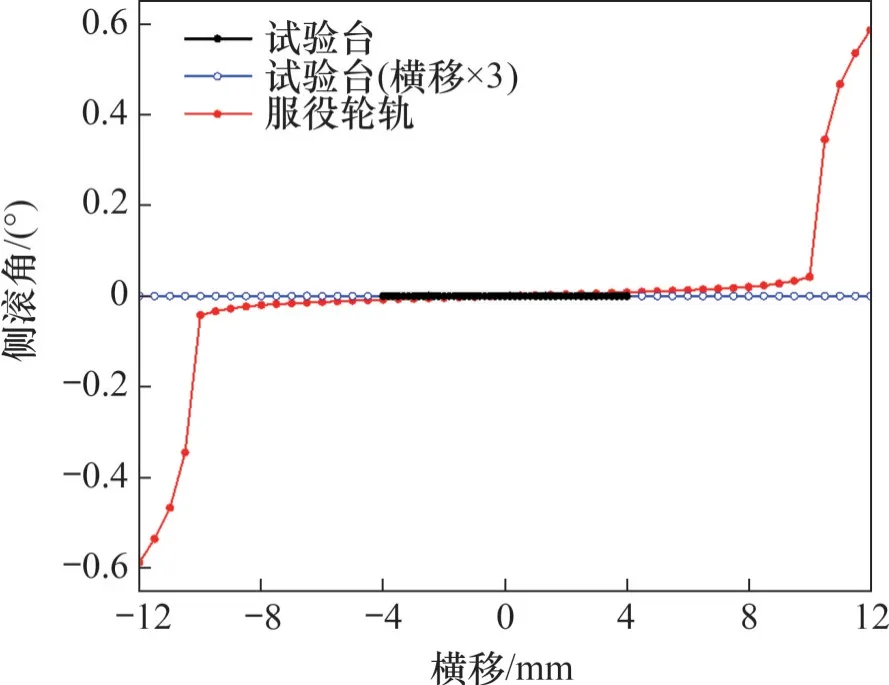
圖14 側滾角隨橫移的變化Fig.14 Variation of roll angle with lateral displacement

總之，試驗臺在車輪橫移為-3.0～1.0 mm 時，能精確模擬服役輪對橫移-9.0～3.0 mm 的接觸工況。當試驗車輪正向橫移超過1.0 mm 直至發生輪緣根部接觸乃至輪緣貼靠，其接觸斑面積、接觸壓力與服役輪軌的相對誤差將變得不可忽略。

3.4 等效應力

不同橫移下，鋼軌內Von Mises 等效應力沿深度方向上的分布如圖15 所示，具體包括橫移為0，1.0(3.0)和3.0(9.0) mm這3種工況。由圖15(a)可見，當車輪無橫移時，試驗臺和服役輪軌的Mises等效應力沿鋼軌深度上呈現同樣的分布規律，分別在鋼軌表面以下1.11 mm 和3.12 mm 處達到最大值，且二者的表面和次表層最大等效應力均基本相等，前者表面等效應力比后者的低1.60%，而前者次表層最大等效應力比后者的低2.51%。當橫移1.0(3.0) mm 時，試驗臺與服役鋼軌次表層最大等效應力之差為6.45 MPa，相對誤差為1.27%，見圖15(b)。當橫移進一步增至3.0(9.0) mm 時，試驗輪軌最大等效應力達到1 293.12 MPa，且出現在鋼軌表層，而服役輪軌的最大等效應力仍然位于鋼軌次表層，二者的相對誤差達到79.09%，使得等效應力沿深度方向分布趨勢也不再具有相似性。

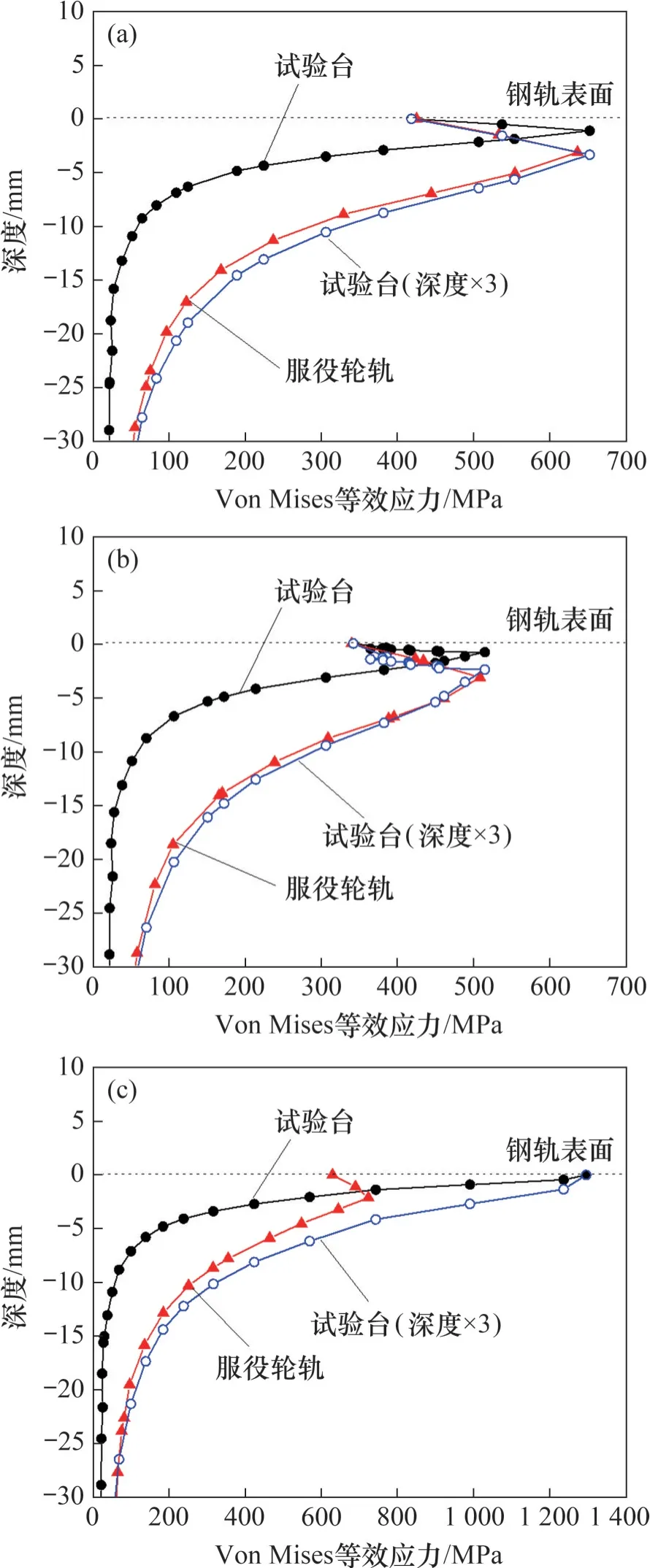
圖15 不同橫移下鋼軌內Von Mises等效應力沿深度方向的分布Fig.15 Distribution of Von Mises equivalent stress in rail along depth direction at different lateral displacements

圖16所示為鋼軌內最大Von Mises等效應力隨橫移的變化。無橫移時，試驗臺和服役條件下的等效應力分別為652.80 MPa 和636.82 MPa，相對誤差為2.51%。試驗車輪橫移-3.0～1.0 mm 時的最大Von Mises等效應力與服役輪對橫移-9.0～3.0 mm間最大Von Mises 等效應力的相對誤差為13.66%。值得注意的是，圖16 中試驗臺和服役輪軌的曲線在該區間內具有相同的變化趨勢，進一步證實了上述試驗臺模擬準則的合理性。更大橫移(趨于輪緣貼靠)時，雖然試驗臺和服役輪軌相應橫移下的最大Von Mises 等效應力均先有所下降，然后劇增，但幅值存在較大差異，例如，橫移3.0(9.0) mm 時試驗和服役軌內最大等效應力分別為1 293.13 MPa和722.07 MPa，相對誤差高達79.09%。

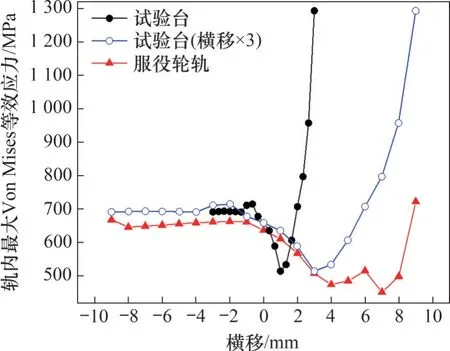
圖16 軌內最大Von Mises等效應力隨橫移的變化Fig.16 Variation of the maximum Von Mises equivalent stress in rail with lateral displacement

4 討論與展望

當輪軌滾動行為模擬試驗臺在車輪橫移為-3.0～1.0 mm時，考慮縮尺比例后，能夠定量地再現實際服役輪軌的接觸壓力、接觸斑幾何、軌內等效應力等，具備精確模擬實際輪軌磨耗和滾動接觸疲勞等損傷的能力。但是，限于試驗臺無法考慮側滾的現實，不能直接模擬更大橫移下的輪軌服役行為。未來若需要模擬大橫移工況，則應考慮在試驗臺上加裝側滾調節裝置，或調整車輪垂向載荷，使接觸壓力或軌內Von Mises 等效應力與現場達到同一水平，但如此間接模擬仍不能修正接觸斑形狀上的差異。需強調的是，本文僅考慮了試驗臺的靜態線彈性接觸狀態，未來尚需深入、全面分析其模擬性能，具體研究工作可從以下幾個方面開展：

1) 設計實物試驗，對比試驗臺和有限元模型的輪軌接觸斑形狀與面積，以增強仿真結果的可靠性。

2) 為試驗車輪加裝懸掛系統，以更好地模擬現實中車輛-軌道動態相互作用。

3) 考慮試驗輪軌瞬態滾動接觸行為、材料彈塑性行為與實際輪軌系統的異同，為試驗臺的研究應用奠定堅實基礎。

4) 建立不同縮尺比例的輪軌接觸有限元模型，以典型變量(如接觸壓力)為指標分析其輪軌接觸相似性，得到車輪-環軌試驗臺的最佳縮尺比例，為同類型試驗臺的設計提供參考。

5) 由于輪軌損傷通常出現在新輪新軌投入使用后或鏇修、打磨后一段時間，未來還需考慮典型磨耗型面接觸的等效準則。

5 結論

1) 在最大接觸壓力和Von Mises等效應力模擬準則下，試驗臺模擬高速輪軌系統時，其垂向載荷分別為10.56 kN和9.34 kN。

2) 車輪與軌枕相對位置對輪軌靜態接觸壓力分布及接觸斑面積的影響可以忽略；正常高速輪對沖角僅造成接觸斑在鋼軌上位置的變化，接觸壓力分布和接觸斑面積幾乎無變化。

3) 試驗臺在車輪橫移-3.0～1.0 mm區間內的接觸壓力分布、接觸斑面積、軌內Von Mises 應力結果均能精確表征服役輪軌對應橫移(-9.0～3.0 mm)下的相應結果。但在更大橫移下，由于試驗臺忽略了側滾角，試驗結果存在不可忽略的誤差。