類矩形盾構隧道上穿施工引起既有隧道剪切錯臺變形研究

傅鶴林，于歸，鄧皇適，吳疆，張凱源

(中南大學 土木工程學院，湖南 長沙，410083)

地鐵具有快速、安全、方便和容量大等特點，為了緩解日益增加的交通壓力，許多城市修建了大量的地鐵線路。已建的地鐵隧道截面大多是圓形，但類矩形截面隧道有更高的空間利用率。自2002年日本采用類矩形單洞地鐵雙線設計之后[1]，越來越多的地鐵隧道采用類矩形截面。我國在2015年修建寧波軌道交通3號線時就首次采用類矩形截面[2]。但由于地下隧道線路繁多，新建的類矩形盾構隧道會不可避免地對下伏既有隧道產生擾動，影響既有隧道結構穩定。因此，研究類矩形盾構隧道上穿施工對既有隧道的影響很有必要。目前新建隧道上穿施工對既有隧道的擾動影響研究主要分為理論分析法[3-7]、數值模擬法[8-11]和模型實驗法[12-13]。在理論分析研究中，LIANG 等[3-4]和李凱梁等[5-6]分別將既有隧道視為Winker地基梁和擱置于Pasternak地基的Euler-Bernoulli梁，分析了新建隧道開挖卸荷影響下既有隧道的豎向變形，但并未考慮盾構正面推力、盾殼摩擦力和盾尾注漿壓力的影響。魏綱等[7]考慮圓形盾構隧道上穿施工影響，運用最小勢能原理結合工程實例求解得到了既有隧道的豎向位移。綜上所述，人們對現有的新建隧道上穿既有隧道的施工研究較少，且大部分研究都是針對圓形截面的新建盾構隧道，但類矩形截面的新建隧道由于斷面收斂形式復雜，盾構正面推力、盾殼摩擦力和注漿壓力分布形式與圓形盾構隧道不同，計算難度大，目前沒有具體的計算模型。因此，考慮類矩形盾構隧道上穿施工的諸多因素，建立相應的力學計算模型，分析類矩形盾構隧道上穿施工對既有隧道的擾動影響很有現實意義。本文根據現有的研究成果建立類矩形盾構隧道上穿施工計算的力學模型，并通過鏡像法和Mindlin 解得到新建類矩形盾構隧道施工過程中土體損失、盾構正面推力、盾殼摩擦力和盾尾注漿壓力所引起既有隧道軸線處的附加應力計算公式。采用剪切錯臺模型，運用最小勢能原理計算得到既有隧道豎向變形、環間錯臺量和剪切力隨施工階段的變化過程，對比分析理論計算結果和數值模擬結果，并通過控制變量法研究多種參數變化對既有隧道變形的影響。

1 計算模型

盾構隧道施工對地層位移產生影響的因素主要有盾構正面推力、盾殼摩擦力、盾尾注漿壓力和土體損失。本文在考慮類矩形盾構隧道上穿施工給既有隧道帶來的影響時，分析了上述因素的共同作用，并在計算過程中假定：1) 土體為均質的線彈性半無限體；2) 類矩形盾構機沿直線掘進，不考慮施工過程中路線偏移或糾偏影響；3)不考慮時間效應的影響。采用鏡像法和Mindlin 解推導土體中附加應力的計算公式，該理論適用范圍十分廣泛，梁榮柱等[7,14-15]使用該理論并作出了相似假設。鄧皇適等[14]運用該理論分析時依托的工程項目地層為砂土地層；魏綱等[7,15]在計算過程中依托的工程案例1[6]、案例2[16]和案例3[17]的地層主要為黏土地層，工程案例4[18]的地層主要為砂土和黏土地層。可見，在一般情況下，本文理論模型可以用于砂土和黏土地層的研究。

根據現有的研究建立如圖1所示的類矩形盾構隧道上穿施工計算模型。圖1 中，盾構刀盤位于XOZ平面上，Y軸方向長度表示在盾構掘進的方向上盾構刀盤與既有隧道之間的距離，X軸方向長度表示距離盾構機中軸線的長度，Z軸方向長度表示從地面往下計算的深度，p為盾構正面推力，f為盾殼摩擦力，q為盾尾注漿壓力。

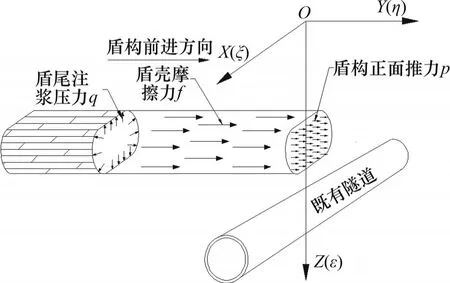
圖1 類矩形盾構隧道施工計算圖Fig.1 Diagram of construction calculation for quasirectangular shield tunnel

2 土體損失產生的附加應力

2.1 鏡像法基本原理

SAGASETA[19]提出了鏡像法，假定土體為半無限體，地下(x0，y0，z0)處半徑為a的空隙在土體中產生的應力由三部分組成：1) 真實源作用下無限體內產生正應力σ0和剪應力τ0；2) 地面以上對應真實源位置的影響匯在無限體內及地表產生的應力；3) 地面上有一個與τ0方向相反、大小為其2倍的切向應力作用，該應力在地面以下各點產生的應力。

通過計算可以得到真實源與影響匯作用下地下某點(ξ，η，ε)處產生的x，y和z方向上第一部分與第二部分附加應力之和σx1-2，σy1-2、σz1-2分別為

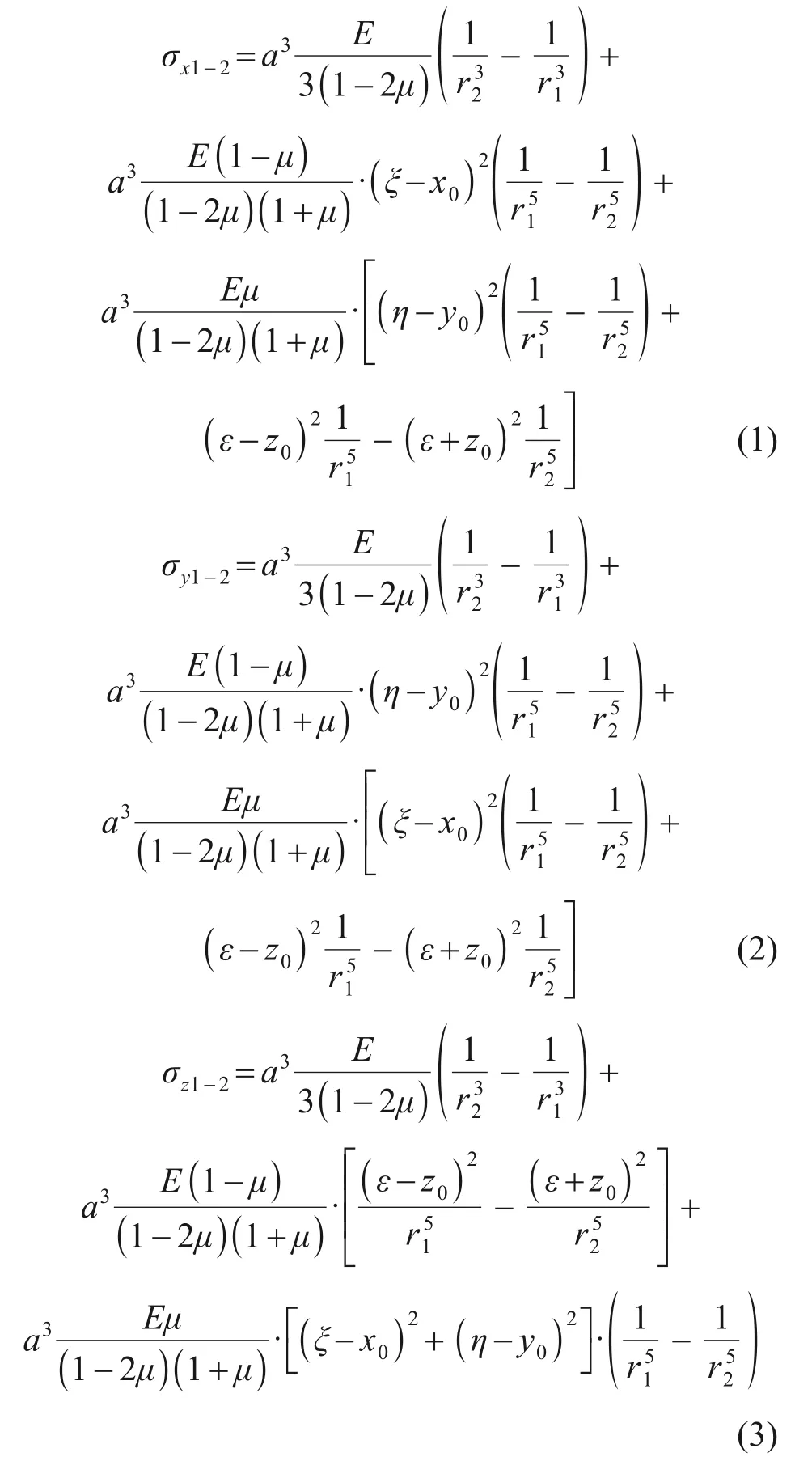
式中：E為土體彈性模量；μ為土體泊松比；(x0，y0，z0)和(ξ，η，ε)分別為圖1所示坐標系下計算點和受力點的坐標；r1和r2分別為

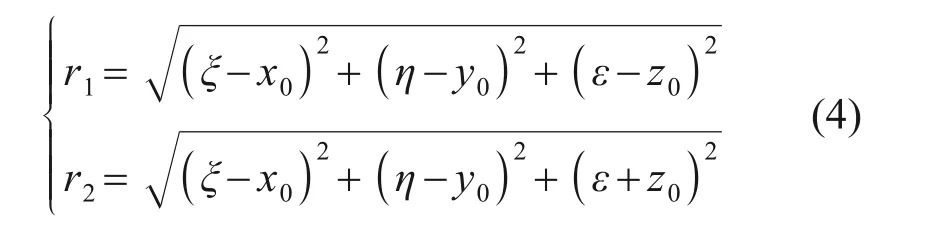
地表處切向應力在地下某點(ξ，η，ε)處產生的x，y和z方向上第三部分附加應力σx3，σy3和σz3分別為

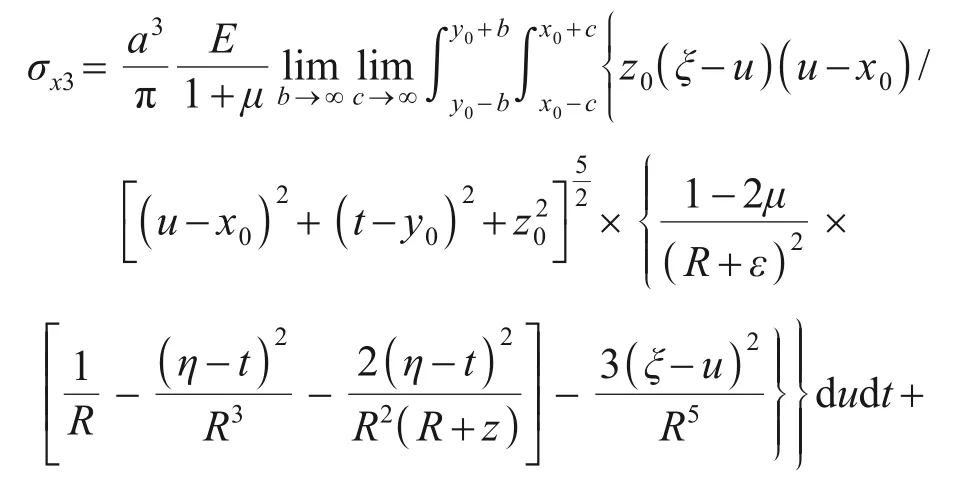
將上述計算得到的土體附加應力疊加，得到半無限土體中(x0，y0，z0)處半徑為a的空隙在點(ξ，η，ε)處產生的總附加應力為

式中：i=x，y，z。

單位體積空隙產生的附加應力為

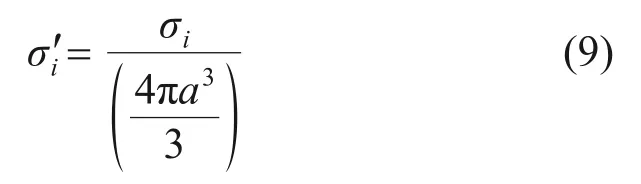
2.2 土體損失產生的附加應力計算

盾構機在掘進過程中，盾構外殼直徑大于隧道管片直徑，盾尾脫出后管片和土體之間仍然存有空隙，在施工過程中一般通過注漿填補空隙，但由于注漿體凝固需要時間以及凝固之后體積減小等原因，在盾尾管片范圍內存在一定的土體損失。依據鏡像法可以計算土體損失在既有隧道軸線處產生的附加應力，在計算過程中需要考慮土體的位移模式。魏綱等[20-21]發現土體的位移模式有3種：1) 等量徑向移動；2) 隧道下沉的非等量徑向移動；3) 隧道上浮的非等量徑向移動。假設類矩形盾構隧道施工時土體的位移模式是隧道下沉的非等量徑向移動，如圖2所示。在計算過程中，將盾構隧道開挖面簡化成由左、右2 個半圓和中間1個矩形組成。圖2中，H為類矩形盾構隧道中心線深度，h為既有隧道中心線深度，h0為2 個隧道之間的間距，d為類矩形隧道開挖面中矩形長邊的寬度，g為土體損失間隙參數。

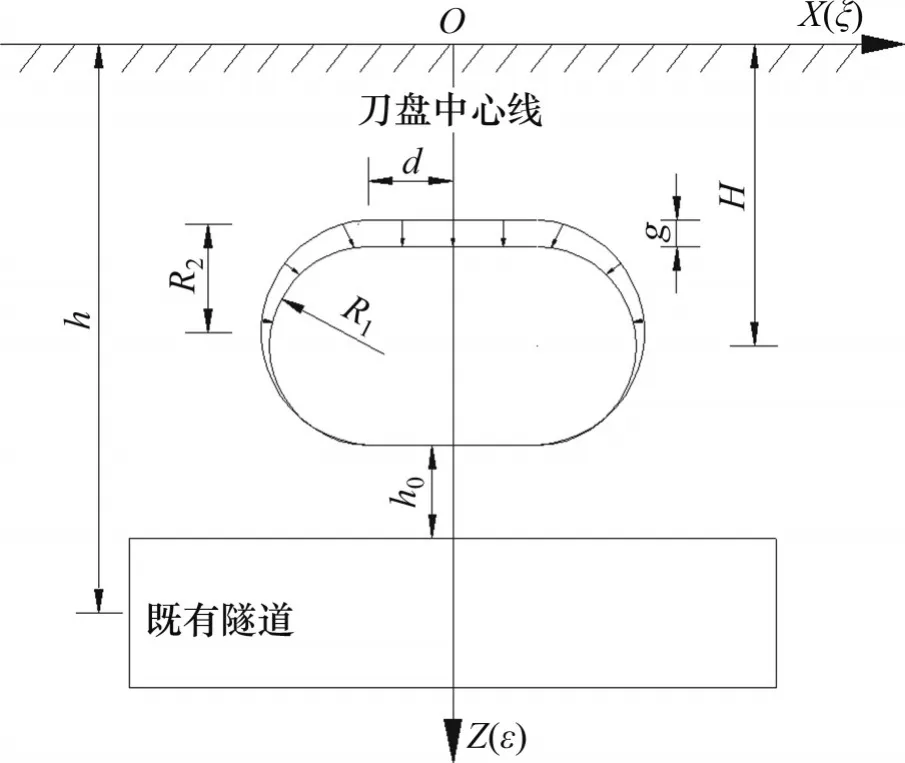
圖2 土體損失引起的附加應力計算圖Fig.2 Calculation diagram of additional stress caused by soil loss

土體損失體積可以看做內外2個相切的類矩形體之間的空隙，類矩形體的長度為l。土體損失體積為V=VR2-VR1。其中，VR2為外側類矩形體體積，VR2=l(πR22+4dR2)，R2為外圓半徑；VR1為內側類矩形隧道體積，VR1=l(πR21+4dR1)，R1為內圓半徑。

將單位體積空隙在既有隧道軸線處產生的附加應力σ′z進行積分，得到土體損失在既有隧道軸線處產生的豎向附加應力σzloss為

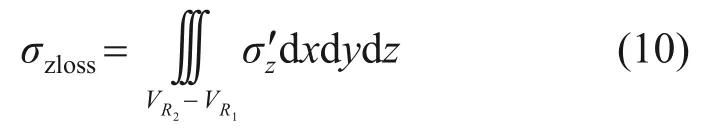
3 盾構施工產生的附加應力

3.1 Mindlin附加應力解

彈性無限均質體中可以用Mindlin 解計算盾構掘進過程中產生的附加應力[22]，計算圖示見圖3。均質彈性無限體中(x0，y0，z0)處作用有水平力ph和豎向力pv，該處作用力在無限體中任意一點(ξ，η，ε)處產生的豎向附加應力σz1和σz2分別為

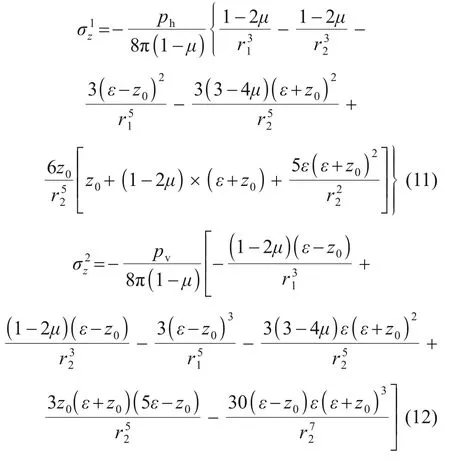
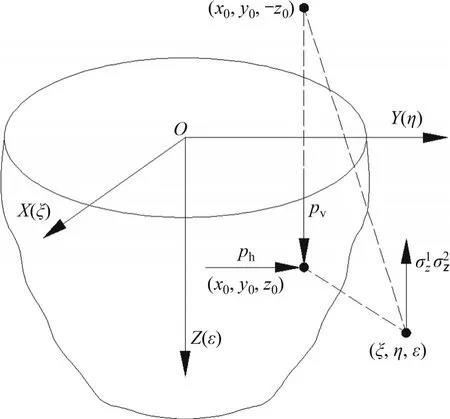
圖3 Mindlin解計算圖Fig.3 Mindlin solution calculation diagram

3.2 盾構正面推力產生的附加應力

盾構掘進過程中的隧道掌子面如圖4所示。圖4中，r為積分點到半圓圓心的距離，θ為積分點與豎直方向間的夾角，x和z分別為X方向與Z方向上的積分點坐標值；掌子面中心坐標為(0，0，H)。在左右半圓上取任一單元dA1=rdrdθ，單元上的正面推力為dFp1=prdrdθ；在矩形部分取任一單元dA2=dxdz，單元上的正面推力為dFp2=pdxdz。將dFp1和dFp2代入式(11)對掌子面進行積分，得到既有隧道軸線處產生的豎向附加應力。積分過程需要變換單元坐標，變換后的坐標為

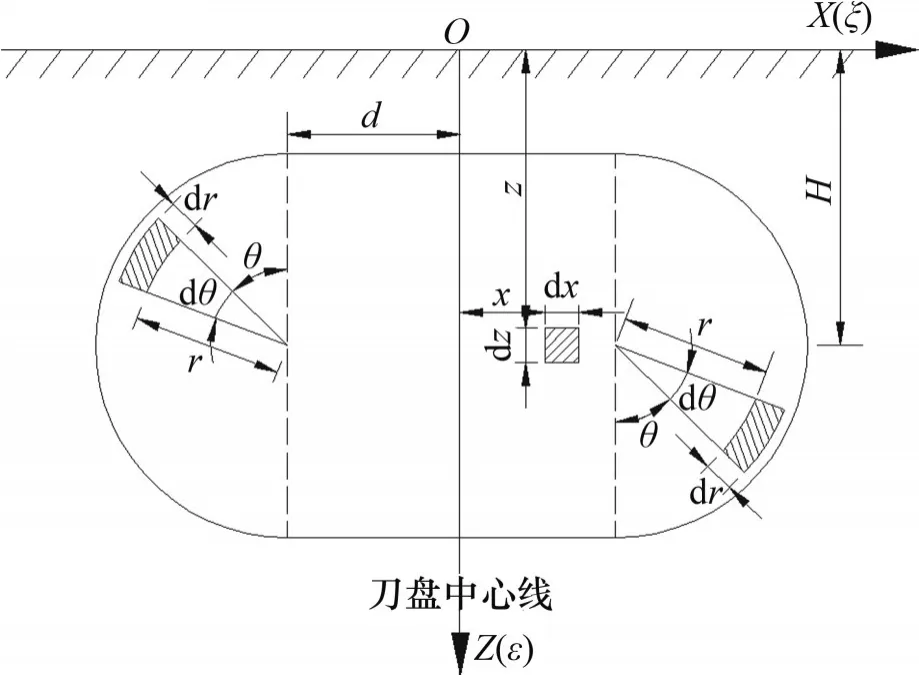
圖4 盾構正面推力引起的附加應力計算圖Fig.4 Calculation diagram of additional stress caused by the front thrust of the shield

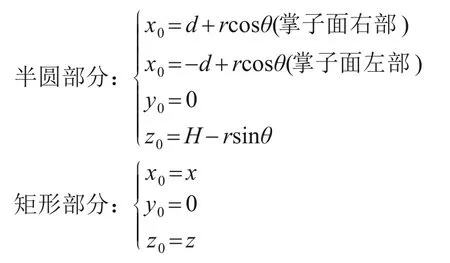
盾構正面推力在既有隧道軸線(ξ，η，ε)處產生的附加應力為

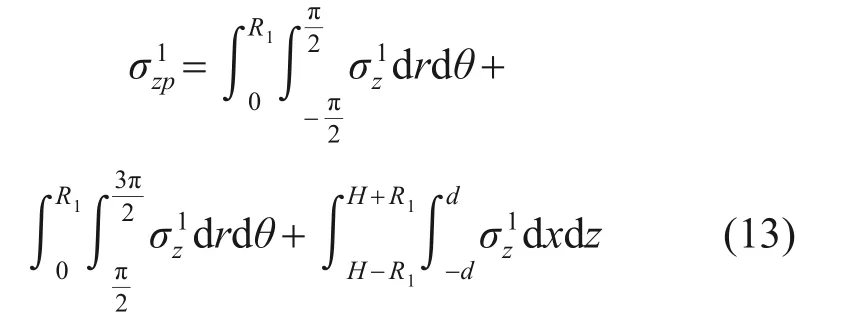
3.3 盾殼摩擦力產生的附加應力

在盾構掘進過程中，機身與周圍土體接觸作用產生的摩擦力會對周圍土體位移產生影響，盾殼摩擦力引起的附加應力計算圖示見圖5。圖5中，s為積分單元與刀盤之間的水平距離，L為盾構機的長度。在左右半圓機身上取任一單元dA1=R1dsdθ，單元上的盾殼摩擦力為dFf1=fR1dsdθ；在矩形機身部分取任一單元dA2=dxdy，單元上的盾殼摩擦力為dFf2=fdxdy。將dFf1和dFf2代入式(11)并在盾殼范圍內進行積分，得到盾殼摩擦力在既有隧道軸線處產生的豎向附加應力。積分過程需要變換單元坐標，變換后的單元坐標為

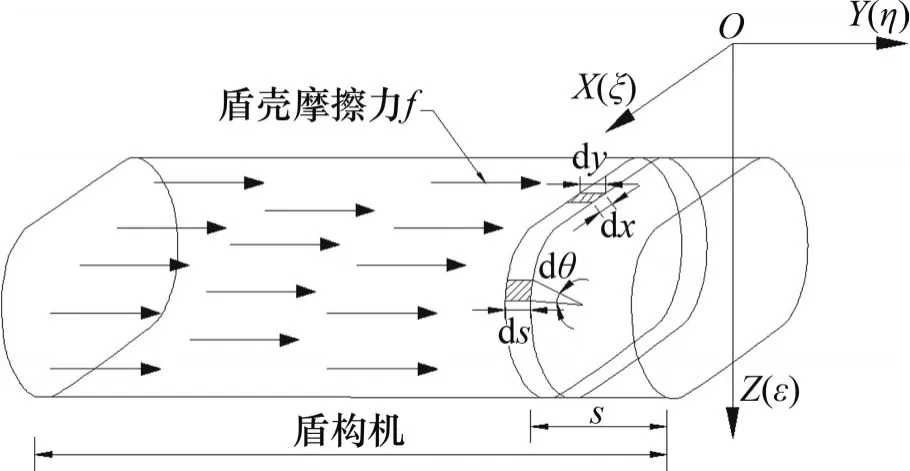
圖5 盾構摩擦力引起的附加應力計算圖Fig.5 Calculation diagram of calculation of additional stress caused by shield friction

盾殼摩擦力在既有隧道軸線(ξ，η，ε)處產生的附加應力為

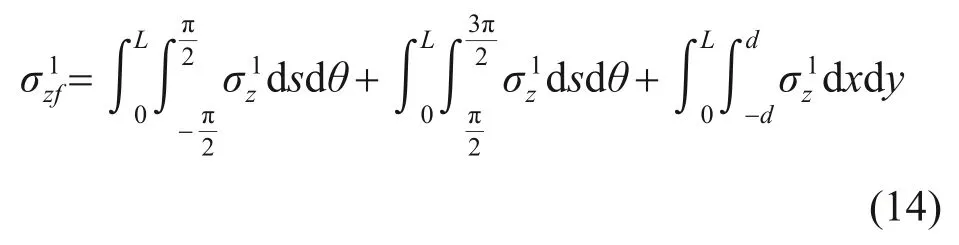
3.4 盾尾注漿壓力產生的附加應力

盾尾注漿壓力q產生的附加應力計算圖示見圖6，盾尾管片長度為α。從圖6可以看到半圓部分處的注漿壓力是沿橫截面徑向分布的，將其分解為水平注漿壓力qx=qcosθ和豎向注漿壓力qz=qsinθ。取盾尾管片半圓部分處任一單元dA1=R1dsdθ，該單元受到的水平注漿壓力和豎向注漿壓力分別為dFqx=qcosθR1dsdθ，dFqz=qsinθR1dsdθ。取盾尾矩形注漿部分處任一單元dA2=dxdy，該單元受到的注漿壓力為dFq=qdxdy。將dFqx代入式(11)，將dFq和dFqz代入式(12)，在盾尾注漿范圍內進行積分，得到盾尾注漿壓力在既有隧道軸線處產生的豎向附加應力和。積分過程需要變換單元坐標，變換后的單元坐標為

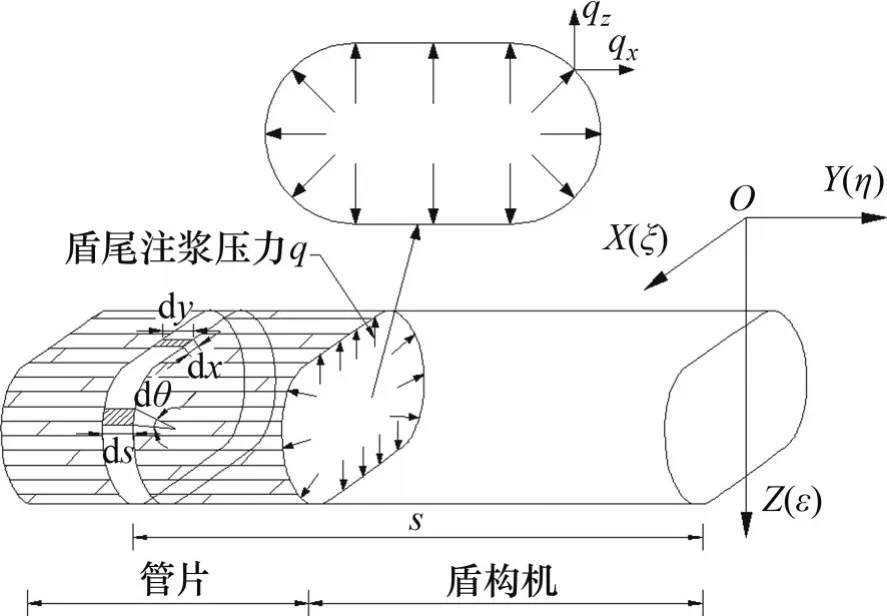
圖6 盾尾注漿壓力引起的附加應力計算圖Fig.6 Calculation diagram of additional stress caused by grouting pressure at shield tail

盾尾注漿壓力在既有隧道軸線(ξ，η，ε)處產生的附加應力為

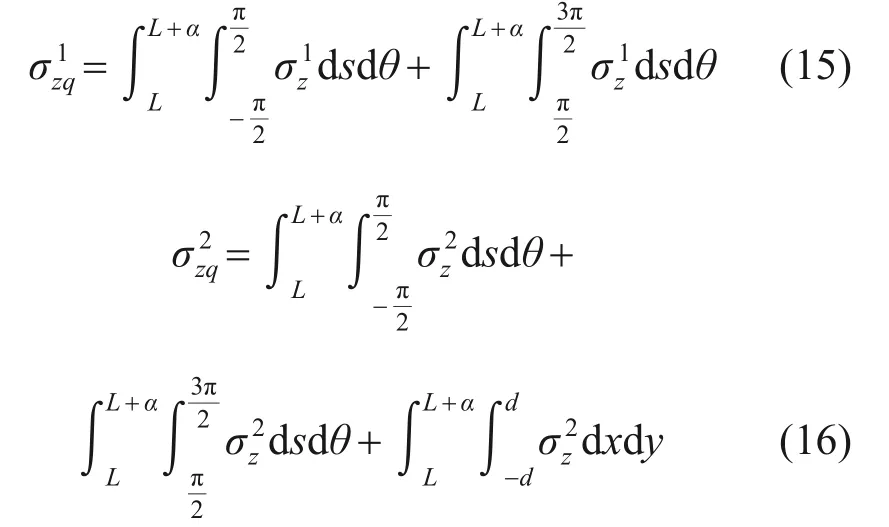
將土體損失、盾構正面推力、盾殼摩擦力和盾尾注漿壓力在既有隧道軸線處產生的附加應力疊加，可得到類矩形盾構掘進過程中既有隧道軸線處產生的附加應力σz為

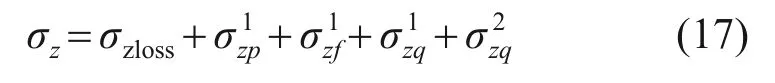
4 基于最小勢能原理計算隧道豎向變形

4.1 既有隧道的總勢能

既有隧道的變形情況可以通過剪切錯臺模型來模擬。在計算過程中，假定長為2S的既有隧道襯砌是由剪切彈簧相連的彈性地基短梁，新建隧道上穿施工導致既有隧道以環間剪切錯臺的方式進行變形[7,23-24]，如圖7所示。

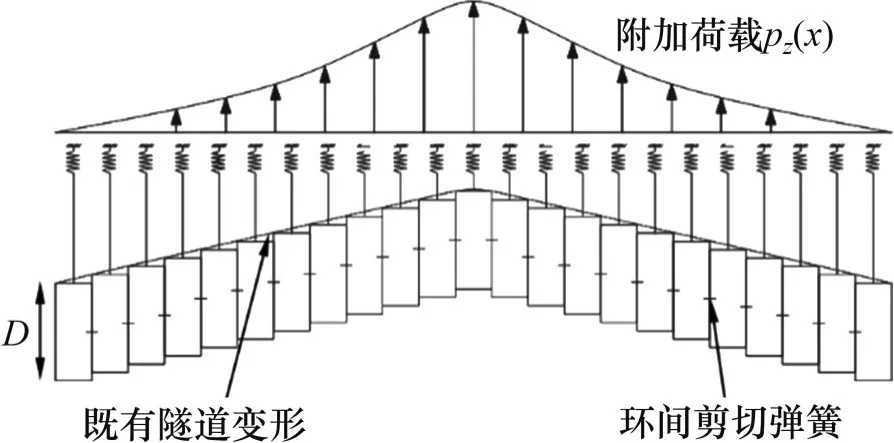
圖7 既有隧道剪切錯臺計算模型Fig.7 Calculation model of shearing dislocation of existing tunnel

對一環寬為ω的既有隧道襯砌環進行受力分析，編號為m，其受到的豎向荷載Fz可表示為

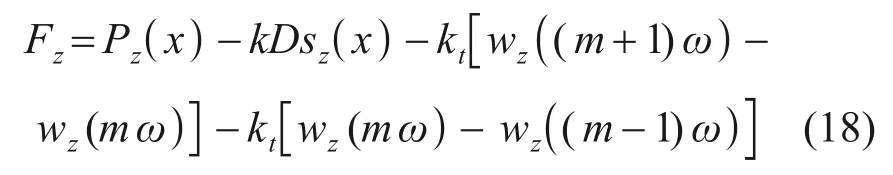
式中：Pz(x)為附加荷載，Pz(x)=Dσz；D為既有盾構隧道直徑；k為地基基床系數，可以通過文獻[24]計算，；Es為地基土彈性模量；EtIt為隧道等效抗彎剛度[25]；kt為隧道的環向剪切剛度；Sz(x)為地基彈簧的位移。根據位移協調條件，Sz(x)=Wz(x)，Wz(x)為既有隧道的水平位移。

根據襯砌環的受力分析可以將既有隧道的總勢能分為3部分：1) 新建盾構隧道施工在既有隧道軸線處產生的附加應力做功Wp；2) 將既有隧道放置在彈性地基上，在產生變形過程中克服彈性抗力做功Wk；3) 既有隧道克服環間剪切抗力做功Ws。具體的計算表達式可以參考文獻[26]。既有隧道的總勢能為

4.2 既有隧道位移函數

運用最小勢能原理過程中，需要假設合適的位移函數來描述受開挖施工影響下的既有隧道變形形狀[26]。假定既有隧道的位移函數服從正態分布函數并進行傅里葉級數展開，既有隧道的位移函數為

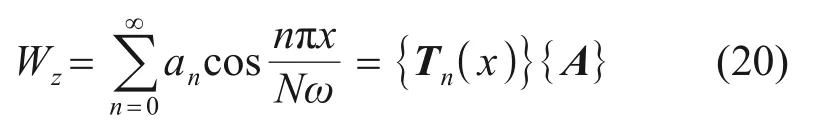
式中：n為傅里葉級數的展開階數；N為受到新建隧道施工影響的既有隧道襯砌環數；Tn(x) =an}，為待定系數。

4.3 變分控制方程

基于最小勢能原理，將既有隧道的總勢能Ep對各待定系數求極值，可得

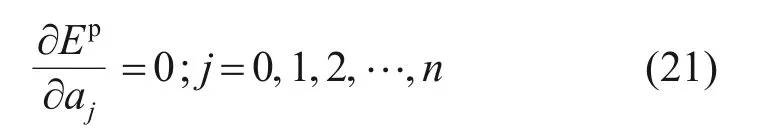
式中：aj為矩陣A中的各個元素。對式(21)進行求解，得到既有隧道的豎向位移控制方程為

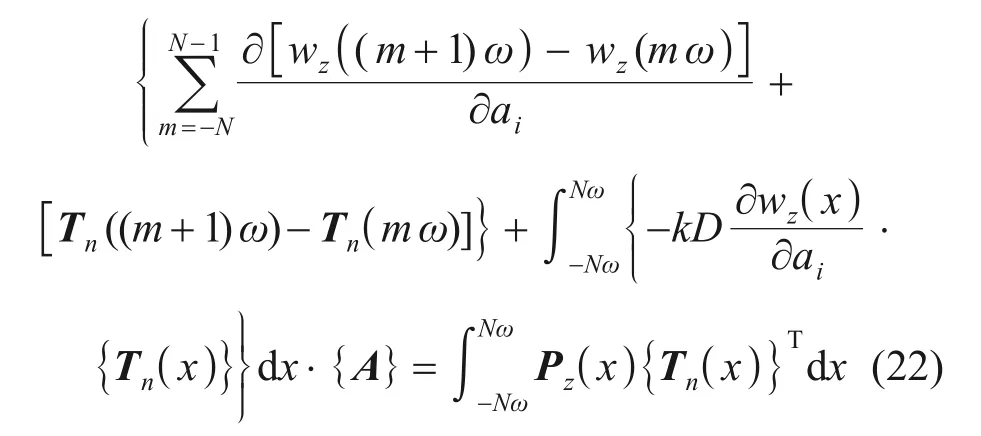
將式(22)表示成矩陣形式：

式中：[Kt]為隧道環間剛度矩陣；[Ks]為土體剛度矩陣。

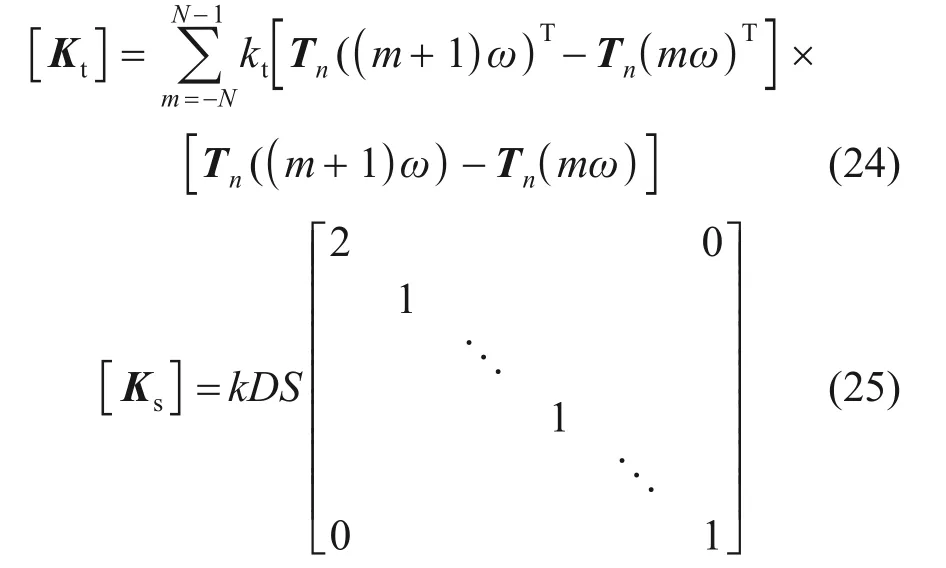
{Pz}T表示隧道襯砌環和自由土體位移之間的相互作用效應，可以表示為

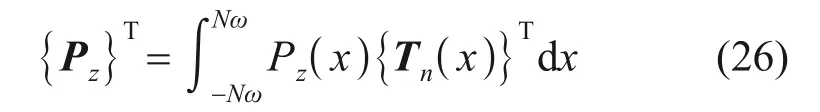
由式(23)得到{A}，代入式(20)可以得到類矩形盾構隧道開挖影響下既有隧道的豎向位移。使用理論公式計算時，除了前面提到的地層適用情況和假設條件外，還需要注意的適用條件是：盾構機的外形為類矩形，沿直線掘進，不考慮掘進過程超挖、欠挖以及土體排水固結等因素的影響。

計算出既有隧道的變形后，可根據相鄰管片之間的豎向位移計算相鄰襯砌管片的環間錯臺量和剪切力。相鄰襯砌管片之間的錯臺量ΔWz為

相鄰襯砌管片之間的剪切力Qz為

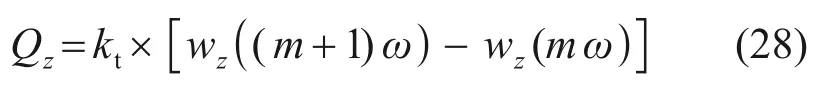
以上算法通過MATLAB 編程進行數值計算，既有隧道的環間剛度矩陣[Kt]和土體剛度矩陣[Ks]取10階即可滿足工程精度要求。

5 工程實例

寧波市軌道交通3號線是我國第一個采用類矩形盾構掘進的試驗段。計算時，采用該路線的類矩形盾構隧道橫截面形狀，具體如圖8所示，圖中各個參數來自文獻[21]，如表1所示。

表1 類矩形盾構隧道幾何尺寸Table 1 Geometric dimensions of quasi-rectangular shield tunnel

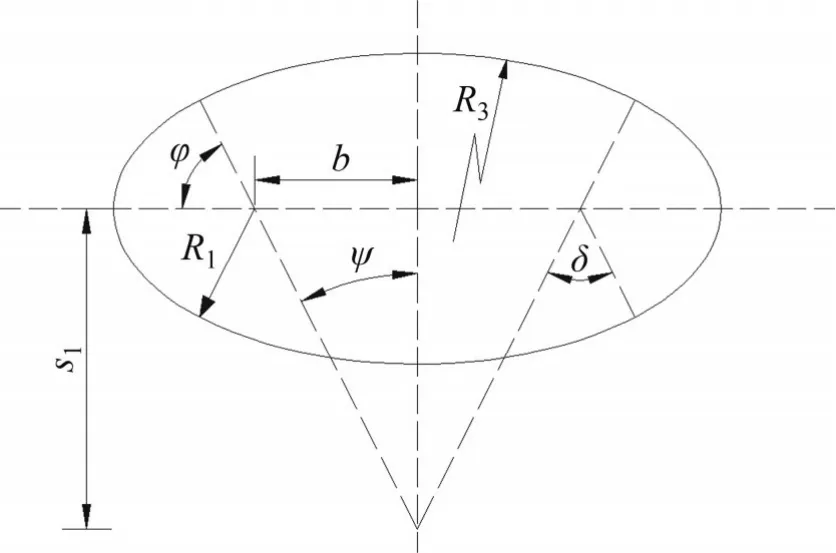
圖8 類矩形盾構隧道橫截面形狀Fig.8 Cross section of quasi-rectangular shield tunnel

對比圖8和圖4可知：實際計算時將類矩形盾構隧道截面簡化成由1 個矩形和2 個半圓形組成。簡化計算不改變實際類矩形截面的長、寬。簡化計算后的截面半圓半徑R1=3.37 m，矩形長邊d=3.5 m，類矩形隧道中心埋深H=13.07 m，土體損失間隙參數g=42 mm。簡化后的截面面積與實際截面面積誤差較小，滿足工程計算精度要求。

類矩形盾構隧道周邊土層物理力學參數如表2所示，既有隧道物理力學參數如表3所示。

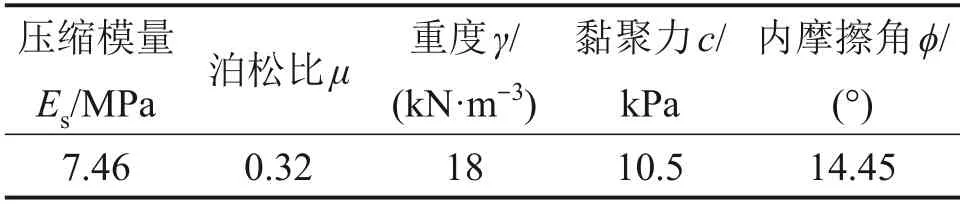
表2 土體物理力學參數Table 2 Physical and mechanical parameters of soil

5.1 對比驗證

根據簡化后的類矩形隧道截面，建立如圖9所示的數值分析模型。新建隧道周圍土體的位移模式選擇見文獻[21]。文獻[21]采用隧道下沉的非等量徑向移動模式，類矩形新建隧道周圍土體位移變化與實際監測情況更加吻合，即在土體位移模式(1)下，理論計算和實際監測的土體變形最大相差約35%；土體位移模式(2)下，變形最大相差約8%；在土體位移模式(3)下，變形最大相差約22%。所以，建模過程中，采取位移控制法使隧道周圍土體強制沉降來模擬土體位移模式(2)，且理論公式也是按照原假定位移模式(2)進行計算。模型中既有隧道與新建隧道之間的距離h0=5 m，構建土體和結構物模型時采用的參數如表2和表3所示，土體遵循摩爾庫侖強度準則，隧道采用線彈性單元。新建隧道從距離既有隧道軸線50 m(y=50 m)開始掘進，總掘進距離為100 m(y=-50 m)。進行計算之前需要對模型施加邊界條件：固定底面位移，上表面為自由變形，約束側面的法向變形。文獻[20,27-28]中盾構推力取20 kPa，均勻分布在刀盤面，故本文取盾構推力為20 kPa。文獻[20]還指出了鋼材和土體之間的摩擦力范圍，在分析過程中將盾殼摩擦力簡化為均勻分布，本文據文獻[20]，取盾殼摩擦力平均值為18 kPa。同時，依據文獻[20]的實測數據反分析，取盾尾處注漿壓力最大為25 kPa，沿盾尾注漿范圍線性遞減。

表3 既有隧道物理力學參數Table 3 Physical and mechanical parameters of existing tunnels

圖9 數值模擬模型Fig.9 Numerical simulation model

為了驗證理論公式的可靠性，將數值模擬結果與和理論計算結果進行對比分析。具體分析的工況是類矩形隧道掘進50 m(y=0 m)時既有隧道的縱向變形情況，以及既有隧道縱向中點位置的變形隨掘進距離的變化情況，并參考文獻[21]中Winker地基梁模型計算方法。文獻[21]在考慮類矩形盾構隧道施工引起既有管線變形過程中，并未考慮盾構正面推力、盾殼摩擦力以及盾尾注漿壓力的影響，本文在應用Winker 地基梁模型中引入上述因素影響進行計算，對比結果如圖10 和圖11所示。

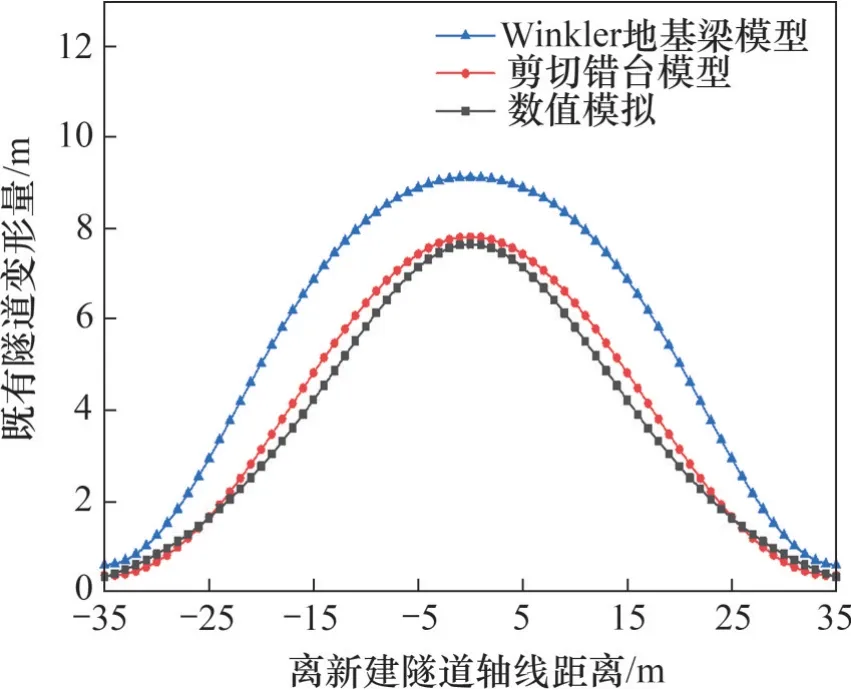
圖10 既有隧道豎向變形曲線Fig.10 Vertical deformation curves of existing tunnels

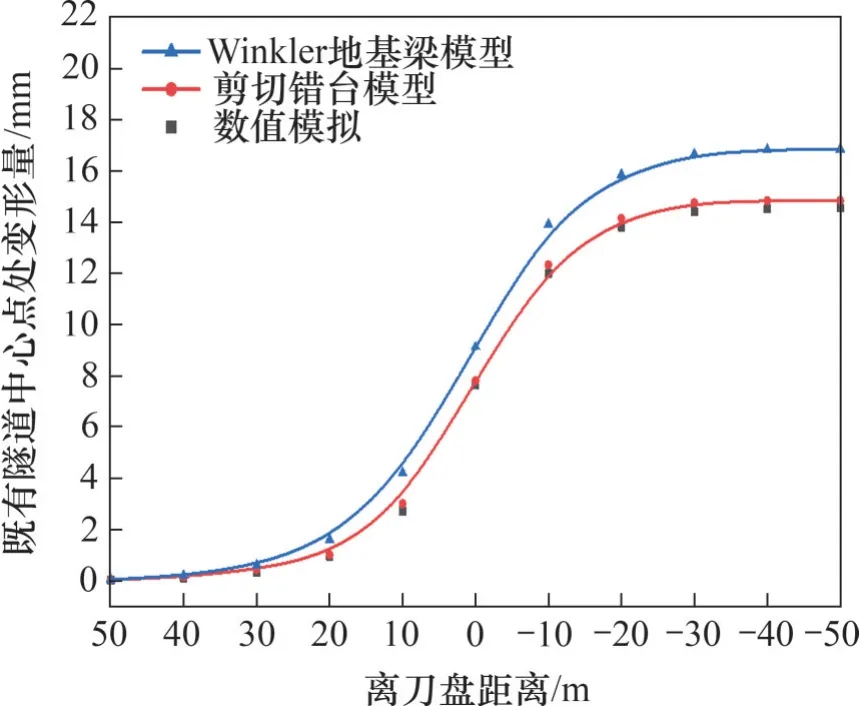
圖11 既有隧道中心點處變形Fig.11 Deformation at the center point of existing tunnel

從圖10 可見：既有隧道變形趨勢一致，即當類矩形盾構隧道掘進至既有隧道上方時，既有隧道產生向上的隆起變形，變形曲線為拱形，拱形曲線最大隆起位于新建隧道軸線正下方；采用剪切錯臺模型計算結果與數值模擬結果擬合最好，在既有隧道各處的變形計算結果誤差較小，且隆起拱的寬度相近，證明使用剪切錯臺模型計算既有隧道受施工擾動產生的變形是可靠的。而Winker 地基梁模型計算的結果與數值模擬結果擬合較差。這是因為使用Winker 地基梁模型時沒有考慮到既有隧道剪切連續性，結果偏大，同時隆起拱的寬度增加。

從圖11 可見：隨著類矩形盾構隧道掘進，既有隧道縱向中心處變形增加平緩，當隧道掘進距離為35 m(y=15 m)時，既有隧道變形開始急劇增大；當隧道掘進距離為70 m(y=-20 m)時，變形趨于穩定(其中，y為盾構刀盤面與既有隧道軸線之間的距離，當y為正值時，表示盾構刀盤面還未通過既有隧道，當y為負值時，表示盾構刀盤面已通過既有隧道)。由于新建隧道開始掘進時，掌子面距離既有隧道較遠，既有隧道受到施工擾動產生的變形較小，3種計算方法得到的結果相近，但隨著掌子面與既有隧道接近，Winker 地基梁模型計算得到的結果開始變大且與其他2種計算方法得到的結果相差較大，剪切錯臺模型計算結果與數值模擬結果相近，并且Winker 地基梁模型得到的既有隧道變形急劇變化段大致為盾構掘進到y=20 m 至y=-20 m段。剪切錯臺模型和數值模擬得到的既有隧道變形急劇變化段大致為盾構掘進到y=15 m 至y=-20 m段。

5.2 環間錯臺量

相較于文獻[21]使用的Winker地基梁模型，使用剪切錯臺模型還能得到既有隧道環間錯臺量。既有隧道的環間錯臺量隨掘進施工的變化如圖12所示。圖12 中，呈正弦函數變化趨勢的曲線代表錯臺量，呈正態分布函數變化趨勢的曲線代表變形量。從圖12 可見：隨著新建隧道掘進，環間錯臺量逐漸增大，當新建隧道掘進距離為70 m(y=-20 m)時，環間錯臺量趨于穩定；最大錯臺量位于既有隧道隆起變形曲線的反彎點處，最大值為0.55 mm；最小錯臺量在既有隧道隆起變形最大處，錯臺量為0 mm，該位置的盾構環基本不發生環間錯臺變形；環間錯臺量對既有隧道的結構穩定性和抗滲性有著重要影響，錯臺量過大可能會引發管片開裂，接縫漏水等不良后果，計算環間錯臺量可為類似工程中的監控量測提供指導。

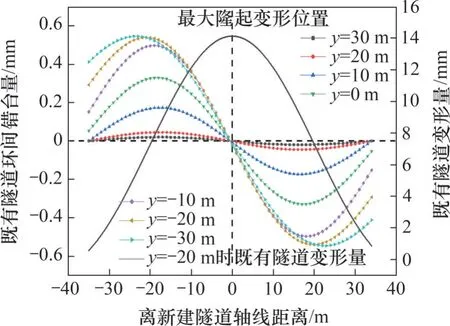
圖12 環間錯臺量變化曲線Fig.12 Variation curves of amount of dislocation platform of existing tunnel pieces

5.3 環間剪切力

新建隧道施工會導致既有隧道盾構環間產生錯動變形，為抵抗變形環間螺栓會承受較大的環間剪切力，當剪切力超過螺栓的剪切強度極限時會發生結構破壞，因此，計算盾構環間剪切力尤為重要。圖13 所示為利用剪切錯臺模型計算得到的環間剪切力隨新建隧道掘進變化曲線。從圖13可見：既有隧道環間剪切力沿既有隧道縱向中心點呈對稱分布；在既有隧道盾構環靠近新建隧道軸線過程中，剪切力先增加后減小，在既有隧道變形曲線反彎處達到最大值，在既有隧道隆起變形最大處達到最小值；隨著新建隧道掘進距離增加，既有隧道環間剪切力逐漸增大，當新建隧道掘進距離為70 m(y=-20 m)時，環間剪切力趨于穩定。

圖13 環間剪切力變化曲線Fig.13 Variation curves of Shearing force of existing tunnel pieces

6 參數敏感性分析

為了更加詳細地分析類矩形盾構隧道上穿施工給既有隧道帶來的影響，以圖10 所示的剪切錯臺模型計算工況為標準工況，采用控制變量的方法，改變單一參數，分析該參數影響下的既有隧道變形情況。

6.1 不同隧道矩形長邊寬度對既有隧道變形的影響

為研究不同矩形長邊寬度的盾構機開挖對既有隧道產生的影響，以隧道矩形長邊寬度為控制變量，只改變標準工況中的d進行對比分析。d分別取2.5，3.5，4.5，5.5和6.5 m，計算結果如圖14所示。從圖14 可以看出：既有隧道最大隆起變形處位于新建隧道軸線正下方，隨著既有隧道遠離新建隧道軸線，隆起變形量逐漸減小；隨著隧道矩形長邊寬度增加，既有隧道產生的隆起變形也隨之增加，且增加幅度變大；既有隧道產生的隆起形狀為拱形，該隆起拱隨著隧道矩形長邊寬度增加而顯著變寬。這是因為隨著隧道矩形長邊寬度增加，掘進過程中產生擾動影響的范圍變大，會使更大范圍內的既有隧道受到影響。

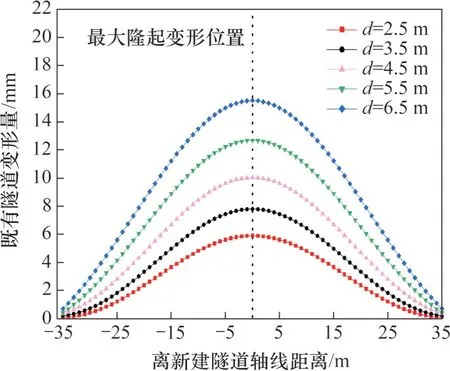
圖14 d不同時既有隧道豎向變形Fig.14 Vertical deformation of existing tunnel for different d

6.2 不同埋深對既有隧道變形的影響

以既有隧道的埋深為控制變量，只改變標準工況中的h0進行對比分析。h0分別取5，6，7，8，9 和10 m，計算結果如圖15 所示。從圖15 可以看出：隨著既有隧道埋深增加，既有隧道產生的隆起量減小，且減小幅度也有所增加；最大隆起變形位置在類矩形盾構隧道中軸線正下方，但既有隧道隆起拱的寬度變化不明顯。這是因為類矩形隧道上穿施工對周圍土體產生擾動影響范圍有限，隨著埋深增加，既有隧道受到的擾動影響減弱，隆起變形減小。

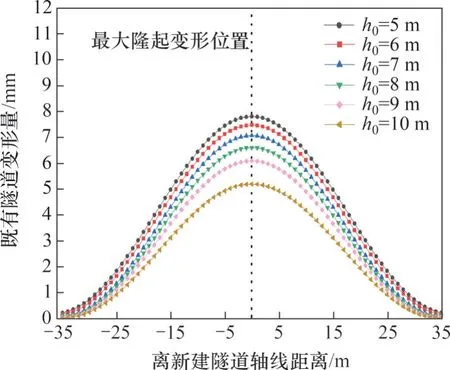
圖15 h0不同時的既有隧道豎向變形Fig.15 Vertical deformation of existing tunnel for different h0

6.3 不同土體損失間隙參數對既有隧道變形的影響

以土體損失間隙參數為控制變量，只改變標準工況中的g進行對比分析。g分別取22，32，42，52 和62 mm，計算結果如圖16 所示。從圖16可以看出：隨著土體損失間隙增大，既有隧道的變形增加，增加幅度增大，隆起拱的寬度也有所增大。這是因為隨著土體損失間隙增大，會有更大體積的的圍巖產生位移，產生更大的土體擾動變形，從而使下伏既有隧道受到更劇烈的擾動，產生更大的隆起變形，隆起拱的寬度也會有所增大。

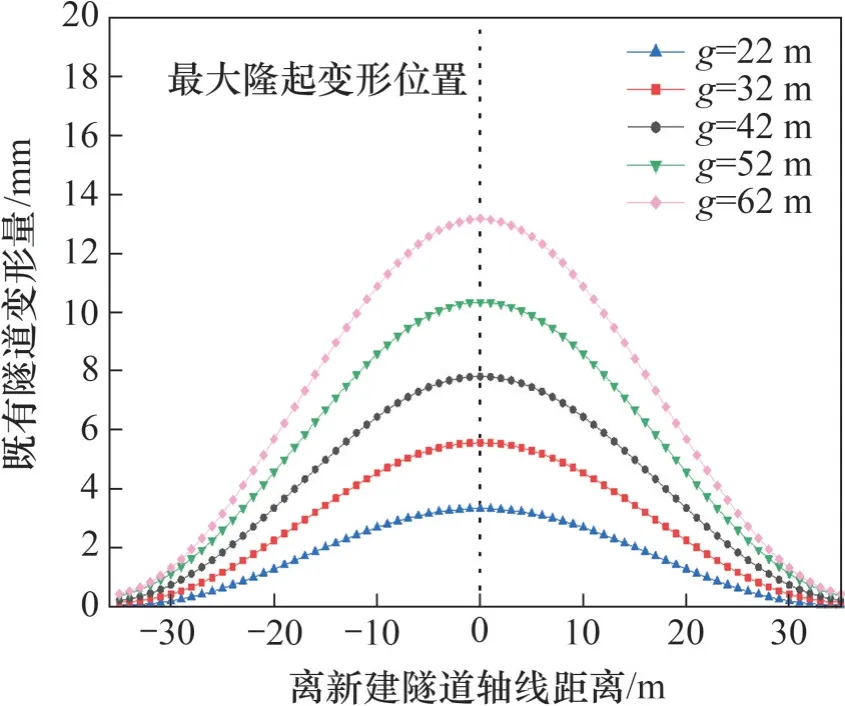
圖16 不同土體損失間隙參數情況下的既有隧道豎向變形Fig.16 Vertical deformation of existing tunnel for different g

7 結論

1) 建立了類矩形盾構隧道施工對下伏既有隧道產生影響的計算模型。采用鏡像法和Mindlin 解推導了類矩形盾構隧道掘進過程中土體損失、盾構正面推力、盾殼摩擦力和注漿壓力影響下既有隧道軸線處產生的附加應力計算公式。基于剪切錯臺模型，運用最小勢能原理得出了既有隧道變形、環間錯臺量和環間剪切力隨新建隧道掘進施工的三維變化曲線。既有隧道變形、環間錯臺量以及剪切力隨著新建隧道掘進而逐漸增大，在盾構機通過既有隧道20 m 后趨于穩定；既有隧道的環間錯臺量和剪切力在變形曲線反彎點處達到最大值，在既有隧道隆起變形最大處達到最小值。對比理論計算結果和數值模擬結果，驗證了理論計算模型和公式的正確性，對類似工程中的監控量測具有重要指導意義。

2) 上穿施工引起既有隧道在新建隧道軸線正下方產生最大隆起變形。隨著隧道矩形長邊寬度增加，既有隧道變形增加，隆起拱寬度顯著增大；隨著既有隧道埋深增加，既有隧道變形減小，減小幅度隨之增大，隆起拱寬度變化不明顯；隨著土體損失間隙參數增加，既有隧道變形增加，隆起拱寬度有所增加。故當新建隧道采用大斷面盾構機以及近距離上穿施工時，需要及時對新建隧道進行加固，并且在上穿施工過程中加強監控量測，注意土體損失不宜過大。

3) 在理論計算過程中將土體看作均質土，而實際上土體是分層的。本文沒有分析既有隧道的水平位移情況，也沒有考慮盾構施工過程中盾構正面推力、盾殼摩擦力和盾尾注漿力不均勻情況，這有待進一步研究。