局部脫冰對導線跳躍高度影響的參數化分析及局部脫冰效應系數研究

張躍龍，樓文娟，黃賜榮，黃銘楓，周為政

(浙江大學 結構工程研究所，浙江 杭州，310058)

輸電線路在遠距離供電中起著關鍵作用，對社會經濟發展至關重要。覆冰導線在氣溫升高、人為敲擊及風力作用下會產生不均勻或不同期脫冰[1-2]。脫冰會導致導線產生嚴重的豎向振動和張力突變，從而引起輸電結構損壞和線路閃絡跳閘[3-4]。導線脫冰引發的最大跳躍高度與局部脫冰的發生位置及其脫冰率緊密相關，現有《電力工程高壓送電線路設計手冊》[5]給出了考慮局部脫冰效應的導線跳躍高度經驗公式，但其中局部脫冰效應系數m的取值范圍為0.5～0.9，未能明確其精細化取值條件，給工程應用帶來一定的困難。為了準確估計導線脫冰跳躍高度以設計合理的電氣絕緣間隙，需要對現有設計手冊中的方法進行改進。

目前，國內外開展了大量有關輸電導線脫冰跳躍高度的研究[6-11]，且大多數研究都是采用非線性有限元方法獲取跳躍高度。有限元仿真模擬雖然綜合考慮了導線-絕緣子串的耦合作用，可用于精細化計算導線脫冰動力響應，但由于仿真分析中建模復雜及迭代計算過程效率低，使其難以應用于大量工程。為了方便、準確地計算導線脫冰跳躍高度，研究者們致力于提出簡潔實用的計算公式，以供設計參考。YAN 等[12]開展了多跨輸電線路脫冰動力響應的模擬，并提出了簡化計算公式來估算最大跳躍高度。GONG 等[13]分析了高差對脫冰后導線跳躍高度的影響，建立了最大跳躍高度與脫冰前后弧垂差之間的函數關系。伍川等[14]基于建立的連續跨輸電線路脫冰簡化模型，從能量、變形和平衡關系等角度出發推導了輸電線路脫冰跳躍高度理論計算方法。XIE等[15]基于動力相似關系設計了某220 kV 原型線路對應的縮尺試驗模型，研究了不同脫冰模式下導線跳躍高度的變化規律，提出了導線脫冰跳躍高度計算公式。HUANG等[16]基于三跨輸電線路縮尺模型試驗，研究了多參數組合下導線脫冰最大跳躍高度，并提出了相應的擬合公式。然而，上述研究成果均忽略了局部脫冰效應對跳躍高度的影響，而考慮線路整體100%脫冰條件的線路設計往往過于保守。現有手冊計算方法[5]通過引入局部脫冰效應系數m來考慮局部脫冰效應，但給定的取值范圍為0.5～0.9，難以應用于實際。

本文采用非線性有限元方法研究脫冰率、冰厚、跨距、高差比、檔數、初始張力及脫冰模式等參數和條件對導線脫冰跳躍高度的影響，分析不同參數組合下跳躍高度對脫冰率變化的敏感程度；研究局部脫冰效應系數m在不同參數組合下的變化規律，并基于最小二乘法提出系數m的精細化計算公式。

1 基于有限元法的導線脫冰跳躍高度計算

1.1 線路參數

由于塔線耦合效應對導線脫冰跳躍高度的影響可以忽略[17]，本文在ANSYS 中建立導線-絕緣子串耦合的有限元模型，采用非線性有限元方法計算得到輸電線路在不同參數下的脫冰跳躍高度。文獻[18]指出輸電線路設計時采用等跨距線路校驗其脫冰動力響應即可，且高差的影響很小，因此，本文以等跨距、無高差的四分裂輸電線路為例展開研究。導線和絕緣子串物理參數分別見表1和表2。

表1 LGJ-400/35導線物理參數Table 1 Physical parameters of LGJ-400/35 conductor

表2 絕緣子串物理參數Table 2 Physical parameters of insulator string

1.2 數值計算方法

在建模過程中，端部采用鉸支座約束，考慮到導線僅承拉而不能承壓的特點，采用桿單元LINK10進行模擬，且導線單元長度取10 m，該單元長度下模型滿足收斂性和精度要求[19-20]。而絕緣子串在導線運動過程中始終處于受拉狀態，其剛度遠大于導線剛度，故采用LINK8單元進行模擬。導線自重沿其長度方向均勻分布，在自重作用下其初始構型為懸鏈線，由于本文線路的垂跨比小于0.1，因此，可以采用拋物線方程進行描述。

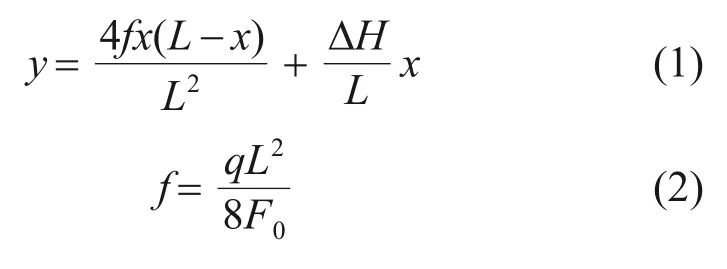
式中：L為導線跨距；ΔH為掛點高差；x和y分別為導線橫、縱坐標值；f為跨中垂度；q為導線單位長度重力荷載。在冰載作用下，導線的非線性運動方程可以表示為

式中：M和Cstr分別為導線質量、結構阻尼矩陣；，和Y分別為豎向加速度、速度和位移向量；F為冰載向量；KT(Y)為考慮幾何非線性效應的切線剛度矩陣，與結構位移向量Y有關。

式中：KL，KN(Y)和Kσ(Y)分別為線性、非線性和應力剛度矩陣。

采用瑞麗阻尼模型來考慮導線的結構阻尼，將結構阻尼矩陣Cstr表示為質量矩陣M和初始切線剛度矩陣KT的線性組合：

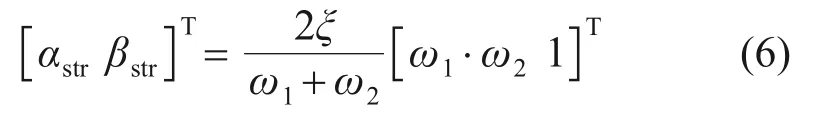
式中：ξ為結構阻尼比，取0.5%；ω1和ω2分別為前兩階振動頻率。

假設導線沿跨均勻覆冰，采用集中力來代替覆冰載荷，通過在導線節點處施加集中力來等效模擬導線覆冰，通過在極短時間內移除集中力來模擬導線脫冰。單位長度導線受到的冰載Fice[21]可以表示為：

式中：ρ為冰的密度；δ為覆冰厚度；n為劃分節點數；Fi為節點i受到的集中力；g為重力加速度。

建立三跨輸電導線有限元模型，如圖1 所示，對導線脫冰跳躍響應展開時域分析，采用無條件穩定的Newmark方法對非線性方程(3)直接求解。

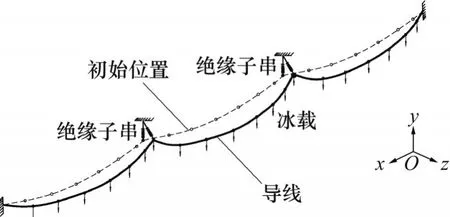
圖1 有限元模型示意圖Fig.1 Schematic diagram of finite element mode

為驗證有限元分析方法的準確性，本文對文獻[16]中脫冰工況8 進行仿真計算，并將有限元計算結果與試驗結果進行對比，如圖2所示。可以看出，有限元計算結果與試驗結果基本一致，驗證了本文所建有限元模型的準確性。

圖2 脫冰豎向位移有限元計算結果與試驗結果[16]對比Fig.2 Comparison of the finite element calculation results in this paper with the experimental results[16] of ice shedding vertical displacement

1.3 有限元計算工況及結果分析

文獻[12]指出所有跨同時脫冰的情況較少，而中間跨脫落往往產生最不利的跳躍高度，因此，本文主要研究中間跨脫冰時的跳躍高度，中間跨脫落細分為均勻脫冰、跨中部脫冰和跨邊側脫冰3種形式，如圖3所示。為研究局部脫冰對導線高度的影響，本文覆冰厚度分別取10，20，30和40 mm；跨距分別取200，300，和400 m(線路等跨距)；高差比(L/ΔH)分別取0，0.1 和0.2，高差比示意圖如圖4所示；檔數分別取1，3和5；初始張力分別取25.06，30.06 和35.06 kN；脫冰率β分別取20%，40%，60%，80%和100%。在不同參數組合下共計180個算例。

圖3 脫冰方式示意圖Fig.3 Schematic diagram of ice shedding modes

圖4 線路高差比示意圖Fig.4 Schematic diagram of line elevation difference ratio

為了研究局部脫冰對導線跳躍高度的影響，定義局部脫冰效應系數m為

式中：Hβ和H100%分別為脫冰率取β和100%時的脫冰跳躍高度。

為了研究不同脫冰方式下導線跳躍高度的差異，計算了跨距為300 m，高差比為0，冰厚為10 mm，初始張力為25.06 kN，檔數為3檔等參數組合下導線脫冰動力響應，相應結果如圖5所示。其中，0～12.5 s時間段導線覆冰，12.5 s時導線部分脫冰。可以看出：在不同脫冰模式下，跳躍高度對脫冰率變化的敏感程度存在差異；當均勻脫冰時，隨著脫冰率從100%減小為80%，跳躍高度的減小幅度明顯比另外2種模式下的大；在跨中部脫冰和跨邊側脫冰模式下，隨著脫冰率增加，導線振動頻率輕微減小，說明局部脫冰會影響導線的振動模式，且不同脫冰方式的影響程度存在差異。在不同脫冰率下，跨中部脫冰時的跳躍高度總是比另外2種脫冰模式下的大，因此，該模式更為不利，在設計中應引起重視。

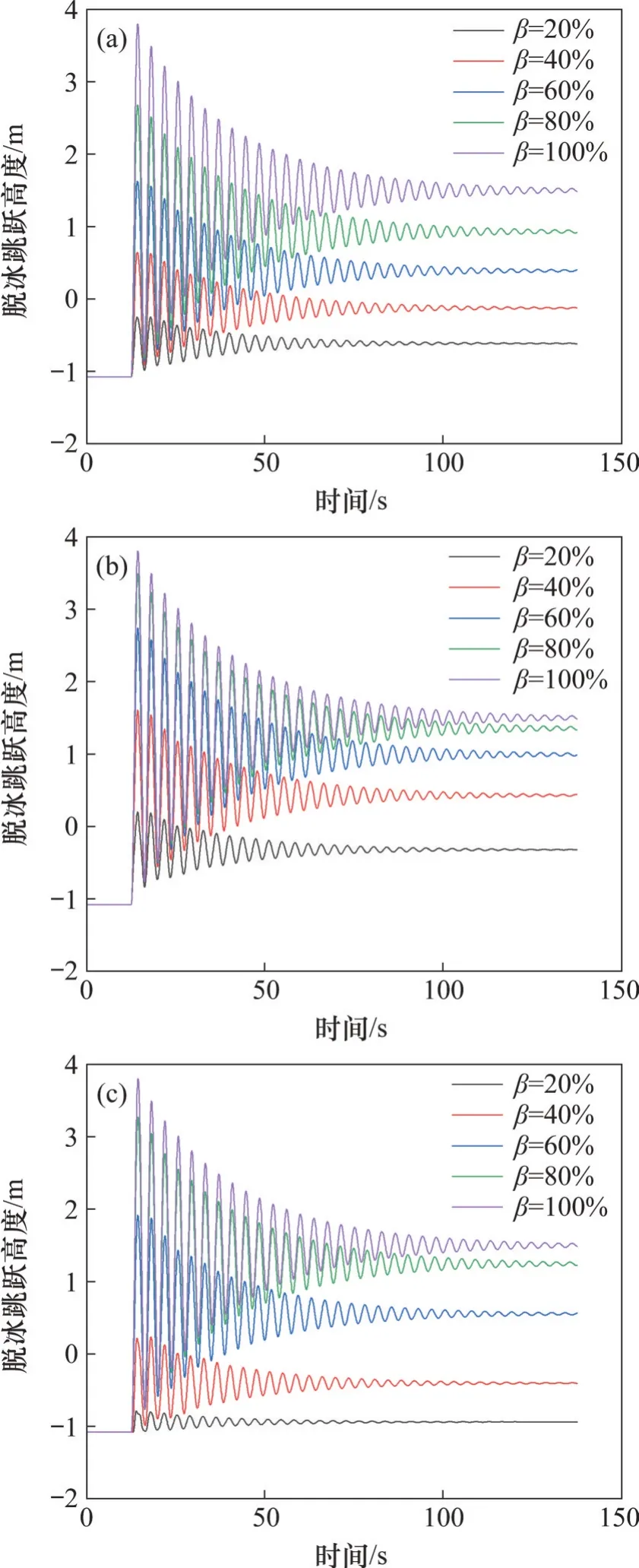
圖5 不同脫冰方式下導線脫冰跳躍高度時程Fig.5 Jump height history following ice shedding under different ice shedding modes

2 局部脫冰影響參數化分析

2.1 覆冰厚度敏感性分析

針對四種覆冰厚度的輸電導線，研究不同脫冰率下導線跳躍高度，如圖6 所示。參數取值如下：跨距為300 m，高差比為0，檔數為3 檔，初始張力為25.06 kN，跨中部脫冰(最不利)。從圖6可以看到：導線脫冰跳躍高度隨覆冰厚度增加幾乎呈線性增加，且隨著脫冰率的增加而增加，但跳躍高度增長幅度隨著脫冰率的增加而逐漸減小；隨著覆冰厚度增加，脫冰率的變化會引起更明顯的跳躍高度差異(斜率增大)。

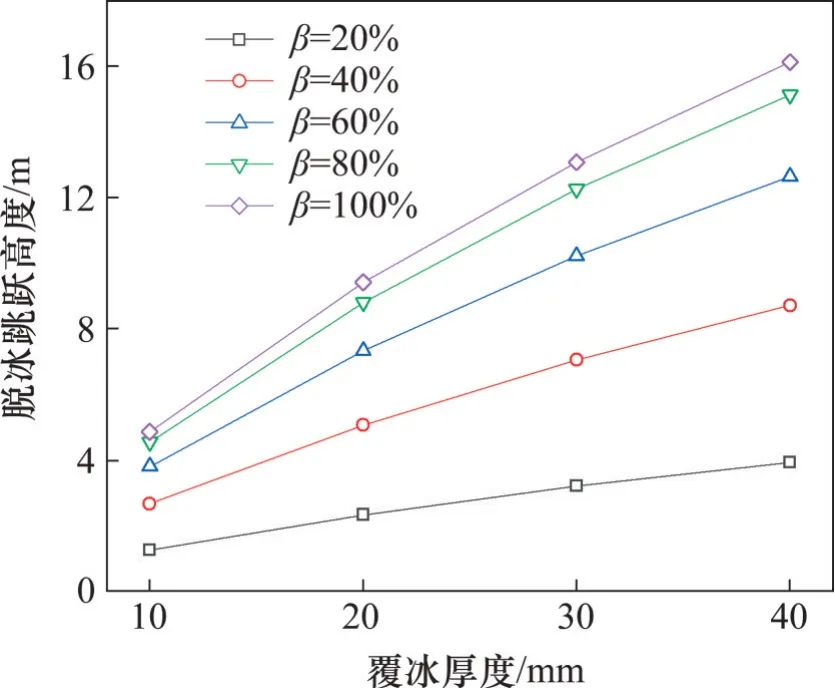
圖6 不同覆冰厚度下導線脫冰跳躍高度Fig.6 Jump height following ice shedding under different ice thicknesses

2.2 跨距敏感性分析

當檔數為3 檔，跨距分別為200 m，300 m 和400 m 時的導線脫冰跳躍高度如圖7 所示，其中，冰厚為10 mm，無高差，初始張力為25.06 kN，脫落方式為跨中部脫冰。從圖7 可以看出：跨距越大，導線脫冰跳躍程度越嚴重，發生閃絡跳閘事故的概率越大，因為跨距越大時，導線脫冰會有更多的勢能轉化為動能，導線跳躍高度越大。隨著跨距增加，脫冰跳躍高度對脫冰率的變化更加敏感。

圖7 不同跨距下導線脫冰跳躍高度Fig.7 Jump height following ice shedding under different span lengths

2.3 高差比敏感性分析

在冰厚10 mm、3 檔、跨距300 m、初始張力25.06 kN等參數組合條件下，跳躍高度隨高差比的變化如圖8所示，此時脫落方式為跨中部脫冰。從圖8可以看出：隨著高差比增大，跳躍高度出現輕微下降(幾乎恒定)，這表明高差的變化對跳躍高度的貢獻很小，可以忽略。在不同脫冰率下，跳躍高度的變化呈相似趨勢。

圖8 不同高差比下導線脫冰跳躍高度Fig.8 Jump height following ice shedding under different height difference ratios

2.4 檔數敏感性分析

針對孤立檔、3 檔、5 檔連續輸電線路，研究不同脫冰率下導線跳躍高度(見圖9)，跨距為300 m，高差比為0，冰厚為10 mm，初始張力為25.06 kN，跨中部脫冰。從圖9 可以看出：跳躍高度隨檔數的增大先增大后減小，在3 檔時取得最大值；隨著檔數增加，脫冰跳躍高度對脫冰率的變化更加敏感。

圖9 不同檔數下導線脫冰跳躍高度Fig.9 Jump height following ice shedding under different number of spans

2.5 初始張力敏感性分析

在冰厚10 mm、3 檔、跨距300 m、無高差等參數組合條件下，跳躍高度隨初始張力的變化如圖10 所示，此時，脫落方式為跨中部脫冰。從圖10 可以看出：隨著初始張力增加，跳躍高度顯示出緩慢下降，這表明張力的變化對導線脫冰跳躍高度的貢獻很小。在不同張力下，脫冰跳躍高度對脫冰率變化的敏感程度差異很小。

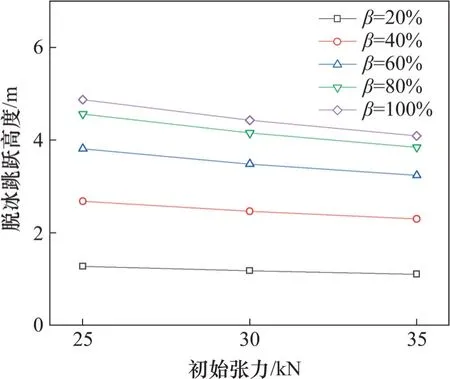
圖10 不同初始張力下導線脫冰跳躍高度Fig.10 Jump height following ice shedding under different initial tensions

2.6 脫冰方式敏感性分析

圖11 所示為3 種脫冰模式下導線跳躍高度，跨距為300 m，高差比為0，冰厚為10 mm，初始張力為25.06 kN，檔數為3檔。圖11中，脫冰模式A，B 和C 分別為均勻脫冰、跨中部脫冰和跨邊側脫冰。對比3 種脫冰模式下的跳躍高度可以看出：當脫冰率β為20%，40%，60%和80%時，跨中部脫冰模式下導線跳躍更劇烈，會產生更大的跳躍高度，在設計中應引起足夠的重視；當脫冰率為100%時，3 種脫冰模式均為中間跨全部脫落，因此，脫冰跳躍高度變化曲線表現為1條水平直線。

圖11 不同脫冰方式下導線脫冰跳躍高度Fig.11 Jump height following ice shedding underdifferent ice shedding modes

3 脫冰跳躍高度計算公式改進

目前，在線路電氣絕緣間隙設計中，通常采用文獻[5]中提供的經驗公式來計算導線脫冰跳躍高度H：

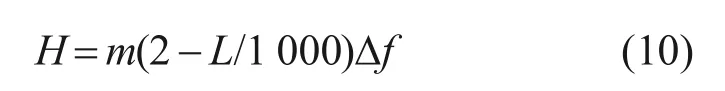
式中：Δf為導線脫冰前后靜止狀態的弧垂差；局部脫冰效應系數m用于表征線路局部脫冰效應，文獻[5]中提供的取值范圍為0.5～0.9，未明確系數m的精細化取值。

本文基于非線性有限元方法，脫冰模式采用最危險的跨中部脫冰，研究冰厚、跨距、檔數、高差比及初始張力等參數組合下，局部脫冰效應系數m的取值情況，如圖12所示。從圖12可以看出：隨著脫冰率β的增大，系數m呈非線性增加，且其增加幅度逐漸減小；在相同脫冰率下，系數m變化很小(幾乎恒定)，這表明參數及其組合工況的變化對系數m的影響很小，在同一脫冰率下，m幾乎為定值。通過最小二乘法擬合這些仿真數據，可以得到95%保證率下系數m的表達式，其擬合結果如圖13 所示。值得注意的是，當m＞1.0 時，m取1.0。

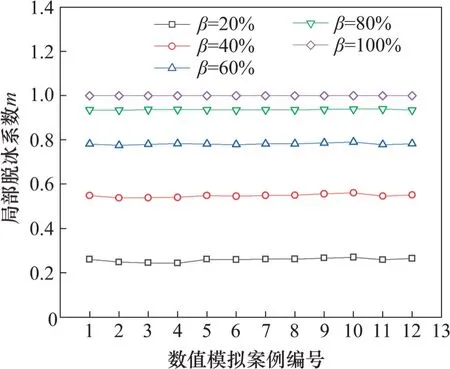
圖12 不同脫冰工況下系數m的變化Fig.12 Changes of factor m under different shedding cases

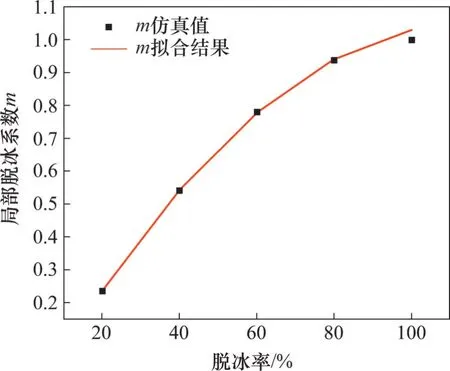
圖13 系數m有限元分析結果與擬合結果對比Fig.13 Comparison of finite element analysis results and fitting results of m

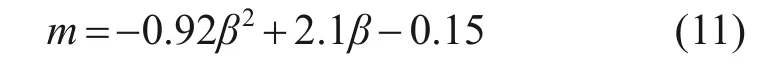
因此，考慮局部脫冰效應的輸電導線脫冰跳躍高度計算公式可以表示為：

式中：qice為導線單位長度覆冰荷載；Hice為導線覆冰靜止狀態的運行張力。

式(11)中系數m的表達式對于不同冰厚、跨距、檔數、高差比及初始張力的線路具有普適性，但系數m是基于跨中部脫冰(最不利)得到的，由于不同脫冰形式可能導致導線脫冰后的振動模式存在差異，因此，式(11)可能不適合其他脫冰形式，但可以采用本文類似的方法得到其他脫冰形式下的系數m。

4 結論

1) 在跨中部脫冰和跨邊側脫冰模式下，隨著脫冰率增加，導線振動頻率減小，說明局部脫冰會影響導線的振動模式，且不同脫冰方式的影響程度存在差異。

2) 在不同脫冰率下，跨中部脫冰時的跳躍高度往往最大，因此，該脫冰模式更為不利，在設計中應引起重視。

3) 脫冰率對導線跳躍高度的影響在很大程度上取決于冰厚、跨距、檔數及脫冰模式，而受高差、初始張力變化的影響較小。

4) 局部脫冰效應系數m主要取決于脫冰率，冰厚、跨距、檔數、高差及初始張力變化對其的影響很小，可以忽略，在同一脫冰率下，m幾乎為定值。

5) 提出脫冰跳躍高度H的計算公式為H=該公式可以更精細化考慮局部脫冰效應，能夠對脫冰跳躍高度進行準確計算。