飛機關鍵部位濕熱環境內外場相似性研究

鄧文亮，吳敬濤，成竹，唐揚剛

（中國飛機強度研究所，西安 710000）

引言

飛機著陸后要逐漸減速到低速狀態，以滑行到指定的位置，可以使飛機減速的方式有三種：其一是通過安裝在起落架上的機輪剎車系統，飛行員控制剎車系統工作，使安裝在機輪上的剎車盤相互擠壓而產生摩擦力，以此來使飛機減速。在剎車盤的作用下，將飛機滑行時的動能轉化為熱能，以自然冷卻或者強制冷卻的形式散熱。這種制動方式效率高，安全可靠。其二是發動機開啟反推裝置。通過安裝在飛機發動機上的反推裝置，改變發動機燃氣的噴射方向，產生與飛機前進方向相反的力，使飛機得以減速。第三種方法是通過安裝在飛機機身以及機翼上的擾流板，使用時向外張開以增大空氣阻力，也可以達到減速的目的，這種方法在飛機滑行速度較高時效果比較好。第二種和第三種減速方式受環境溫濕度因素影響較小，濕熱的外場環境不足以產生明顯的影響。機輪剎車方式由于其制動力全部來自于剎車盤之間的摩擦作用，剎車盤的摩擦力直接關乎制動力的大小。根據摩擦力的計算公式f=μF，其中μ為滑動摩擦系數，F為正應力，在剎車系統提供的正應力一定的條件下，剎車盤提供的摩擦力與其滑動摩擦系數成正比，目前碳/碳復合材料制成的剎車盤因其優異的耐磨性和散熱性得到了大量應用。停放在外場的飛機，由于溫濕度的改變，其剎車盤的摩擦系數也會發生變化，進而導致了飛機的制動距離與預期的偏差。

本文開展了濕熱環境試驗相似性表征與準則研究，進行了濕熱內外場環境試驗，通過典型工況的外場環境穩態響應與實驗室環境穩態響應測量數據對比分析，研究了剎車材料濕熱環境下的摩擦系數的擬合方法，基于合適的擬合方法對濕熱內外場環境試驗相似性進行了研究，通過基于內場擬合曲線的縮放變換的方式，較好地將內場擬合曲線變換為外場擬合曲線，從而得到飛機關鍵部件濕熱環境試驗相似性表征方法，并提出了相似性準則。

1 理論分析

通過基于BP神經網絡的摩擦系數模型，利用反向傳播來調整網絡的權值和閥值，使網絡誤差的平方和最小。BP神經網絡具有強大的非線性映射能力和泛化功能，任一連續函數或映射均可采用3層網絡加以實現。網絡結構如圖1所示。

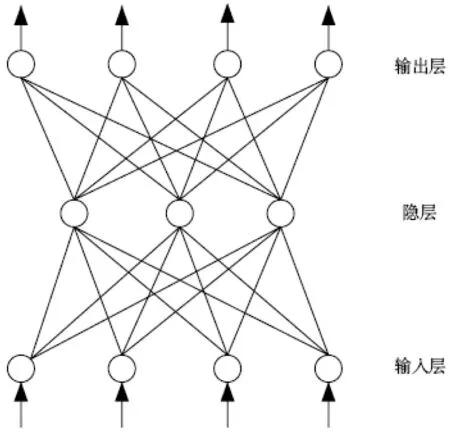
圖1 BP神經網絡結構示意圖

在飛機剎車過程中，剎車力矩和剎車盤摩擦系統是相互耦合，互相影響，剎車溫度、飛機速度處于變化狀態，剎車盤摩擦系數、剎車力矩也是變化的。由于剎車盤摩擦系數的影響因素主要包括剎車盤溫度、剎車力矩和剎車機輪速度，因此建立以剎車盤溫度（℃）、剎車力矩（Nm）、機輪速度（m/s）為輸入，以摩擦系數為輸出的神經網絡結構，以確定任意條件下的摩擦系數。

采用三層BP網絡結構[1]，各層輸入與輸出關系為：

式中：

N—隱含層個數xi（i=1，2，…，N）為輸入信號；

θm—閾值；

ωim—從神經元m到神經元i的連接權值。

輸入參量：

式中：

T —剎車盤溫度；

P—剎車力矩；

v—機輪速度。

2 實驗設計與裝置

2.1 試驗裝置

為了研究濕熱外場環境對剎車盤剎車材料摩擦系數的影響，參考GB-10006，設計了剎車盤剎車材料濕熱環境摩擦系數測試實驗，在外場試驗中，將剎車材料置于外場環境中保持一段時間，使試樣與外場環境的溫度和濕度達到穩態，然后使用摩擦系數測試儀測量剎車材料在當前所處環境下的摩擦系數。進行內外場試驗使用ZJ-MC02型摩擦系數測試儀，測試精度為0.05 %FS，如圖2所示，該摩擦系數測試儀主要由水平試驗平臺、滑塊、驅動機構及測力系統構成，其中水平試驗臺由平整的非磁性材料制成，平臺上嵌有用于調整水平狀態的水平泡，滑塊用于裝載試樣，驅動機構可以帶動滑塊勻速運動，速度可以在0～500 mm/min之間無級調節，測力系統可以測出拉動滑塊的力，用于計算摩擦系數。

圖2 ZJ-MC02型摩擦系數測試儀

2.2 摩擦材料試樣

實驗材料為用于飛機剎車盤制造的碳復合材料，為了便于實驗過程中摩擦系數的測量，參考GB-10006對試樣材料進行了加工處理，其中用于摩擦的下試樣加工尺寸（長×寬×高）為133×63×7 mm，上試樣的加工尺寸（長×寬×高）為63×63×7 mm，試驗材料及試樣如圖3所示。

圖3 試驗材料及加工好的試樣

2.3 實驗過程

在珠海以及上海進行了濕熱環境下剎車盤剎車材料摩擦系數測試試驗，試驗溫度范圍（29.3～39.3）℃，在正式試驗前進行了預實驗，為可能出現的問題制定預案。試驗開始前先將試驗平臺調至水平狀態，調整設備使其處于正常工作狀況下。因外場環境溫度和濕度處于波動狀態中，故每次測試中記錄三次溫度和濕度數據。

3 內外場實驗數據處理與分析

在外場試驗中，進行了溫度（29.3～39.3）℃范圍內共32組有效試驗，包含外場試驗動摩擦系統測試和靜摩擦系統測試，內場試驗中，進行了（50～90）%濕度范圍內的試驗，每種濕度工況下測量了（31～39）℃五種溫度下的摩擦系數，包含外場試驗動摩擦系統測試和靜摩擦系統測試。在外場試驗中，溫度和濕度隨著環境的變化而變化，為了便于數據的擬合，找尋內外場試驗之間的相似性，采取控制變量的辦法先對數據進行選擇。以動摩擦系數為例，將濕度控制在70 %左右，溫度作為自變量，截取出內外場試驗的部分數據，以此數據研究溫度對動摩擦系數的影響；然后將溫度控制在35 ℃左右，以濕度為自變量，研究濕度對動摩擦系數的影響。通過研究溫度和濕度對動摩擦系數的影響，進行內外場試驗的相似性研究。

3.1 內外場試驗數據擬合方法一

以溫度為自變量的內外場動摩擦系數試驗數據如表1所示。

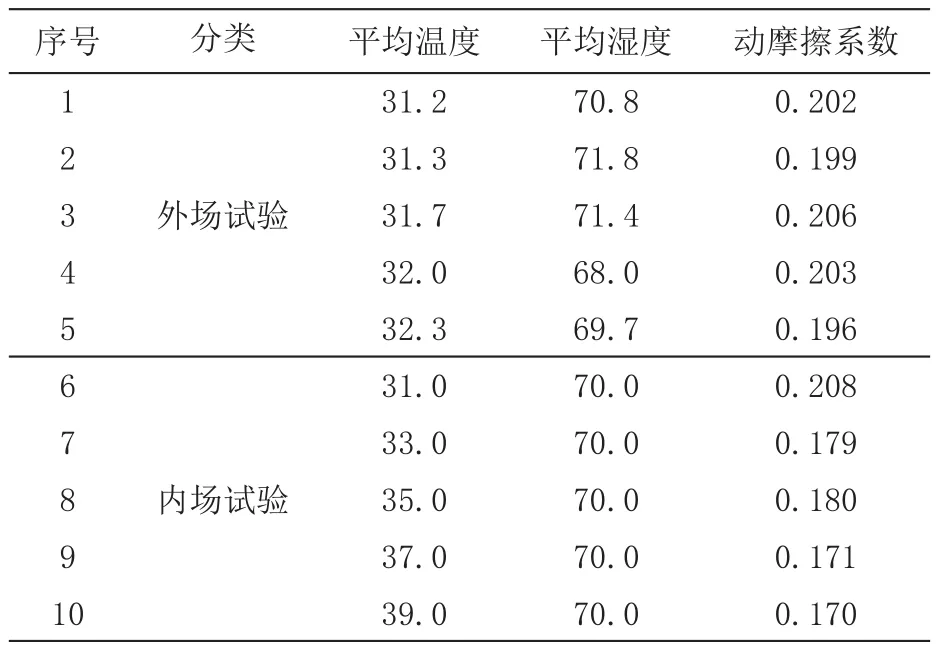
表1 材料動摩擦系數內外場試驗部分數據

為了研究摩擦系數內外場的相似性與相似性表征方法，選擇合適的擬合曲線進行擬合，以擬合優度作為評價指標，在嘗試過多種擬合模型之后，選擇指數擬合、Gaussian擬合、線性擬合、一次多項式擬合模型對內外場數據進行擬合，擬合情況及擬合優度見表2。

綜合分析各擬合模型的擬合優度，見表2，以上四種擬合模型對于內場試驗數據的擬合優度尚可，在0.7以上，其中線性擬合的擬合優度最好，在對外場試驗數據的擬合中，四種擬合模型的擬合優度出現了兩極分化，Gaussian擬合模型以及線性擬合模型因其擬合曲線與試驗數據點貼合度較好而擬合優度較高，但其擬合曲線與內場試驗數據擬合曲線相似性較差；指數擬合模型以及一次多項式擬合模型因其擬合曲線比較“直”而擬合優度較差，其擬合曲線與內場試驗數據擬合曲線在曲線形狀上較為接近。

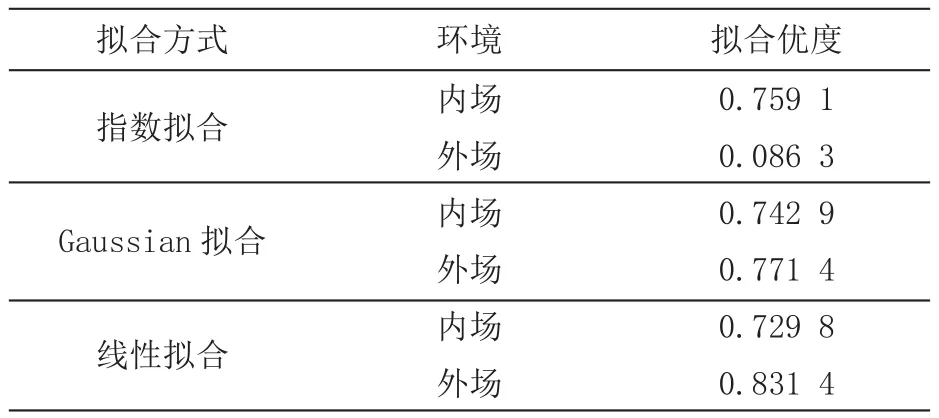
表2 各擬合模型的擬合優度

3.2 內外場試驗數據擬合方法二

以濕度作為自變量的內外場動摩擦系數試驗數據如表3所示。

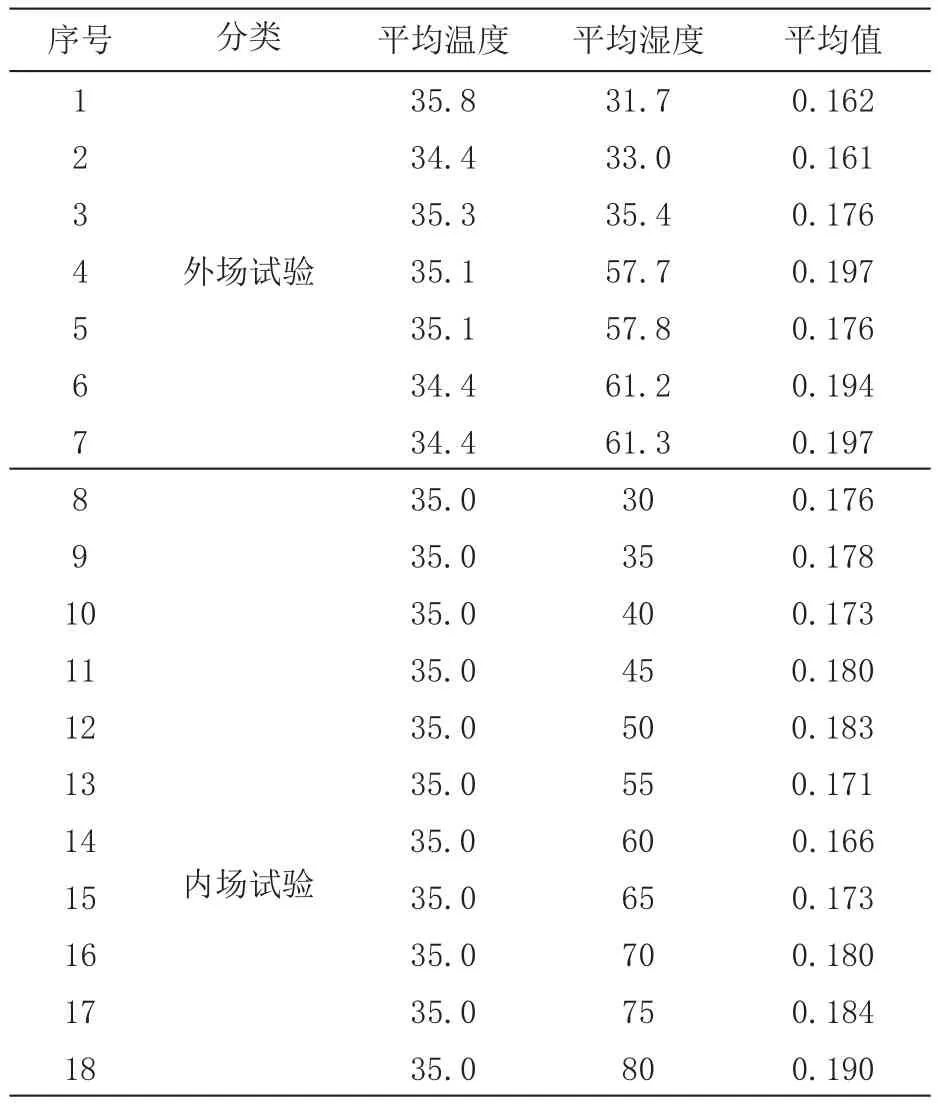
表3 材料動摩擦系數內外場試驗部分數據

以擬合優度作為評價指標，綜合考慮內外場擬合曲線的相似性，選擇多種擬合模型進行數據擬合，在嘗試過多種擬合模型之后，選擇指數擬合、一次多項式擬合以及冪函數擬合模型對內外場數據進行擬合，擬合情況及擬合優度見表4。

綜合分析各擬合模型的擬合優度，見表4。根據各擬合模型的擬合曲線，動摩擦系數與濕度呈明顯的正相關關系，即隨著濕度的升高，動摩擦系數逐漸增大。上述三種擬合模型對于外場試驗數據的擬合效果較好，整體高于0.7，其中以冪函數擬合模型的擬合效果最好，對于內場試驗數據的擬合，各擬合模型的擬合優度相對較低，其中以冪函數擬合的擬合效果最好。

表4 各擬合模型的擬合優度

4 內外場試驗相似性研究

4.1 溫度對動摩擦系數的影響

在研究溫度對動摩擦系數的影響的過程中，通過選擇合適的曲線，對實驗得到的散點數據進行相關性擬合，嘗試選擇平移內外場同類實驗的擬合圖像，通過選擇基于內外場溫度實驗結果的實驗溫差，對內場試驗擬合曲線進行平移，并通過R2評價研究內場試驗擬合曲線平移后與外場試驗數據的相似性。平移變換情況及擬合優度記錄見表5。

綜合分析各擬合模型的平移量與擬合優度，見表5。對比四種擬合模型平移變換擬合優度，其中線性擬合模型擬合優度最好，指數擬合模型擬合優度最差，Gaussian擬合模型對實驗數據散點擬合效果較好，對平移變換后的擬合曲線，其擬合表現不佳。從宏觀來看，四種擬合模型的擬合效果整體欠佳，這與外場試驗數據的分散性有一定的關系。

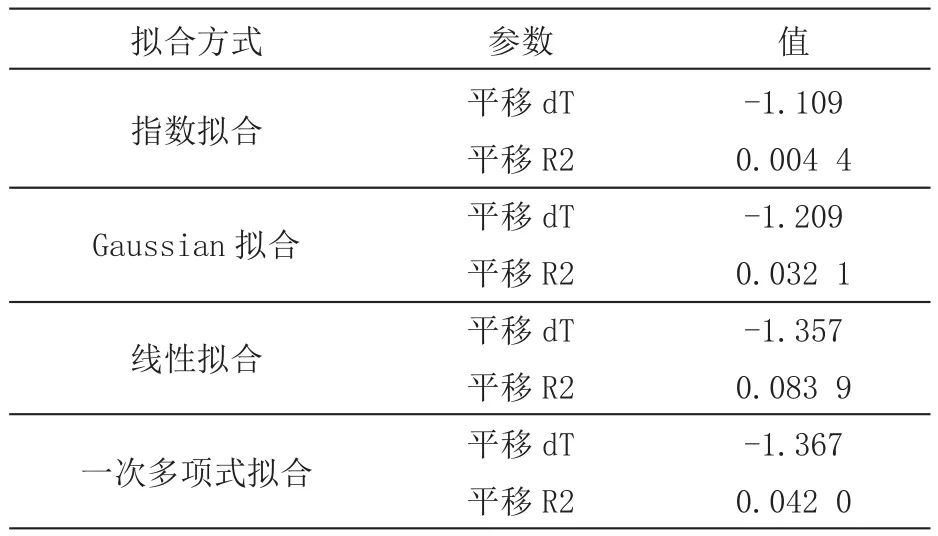
表5 各擬合模型的平移量與擬合優度

4.2 濕度對動摩擦系數的影響

在研究濕度對動摩擦系數的影響的過程中，采取類似的方法，平移內外場同類實驗的擬合圖像，通過選擇基于內外場試驗結果的濕度差，對內場曲線進行平移，并通過R2評價研究內場試驗擬合曲線平移后與外場試驗數據的相似性。平移變換情況及擬合優度記錄見表6。

綜合分析各擬合模型的平移量與擬合優度，見表6。在內外場試驗結果的相似性分析中，采用冪函數擬合模型的內場試驗擬合曲線與外場試驗擬合曲線在曲線形狀上相似性較差，采用平移變換的擬合優度不佳，故在內外場相似性分析中，不采用冪函數擬合模型。根據各模型平移變換的擬合優度，一次多項式擬合模型的擬合優度相對較高，但從整體來看，采用兩種擬合模型將內場試驗擬合曲線平移，其對外場試驗的擬合效果不佳，只在一定程度上可以代替外場試驗的效果。

表6 各擬合模型的平移量與擬合優度

5 內外場試驗相似性表征方法研究

5.1 溫度作為影響動摩擦系數的自變量的表征方法

以溫度作為影響動摩擦系數的自變量，根據之前的相似性研究，可以通過對內場試驗擬合曲線進行平移變換來近似表達外場試驗，為確保試樣基于內場曲線的外場導出曲線的精度、曲線特征和相似性，選擇縮放平移的方式對曲線進行變換。指數擬合模型進行縮放變換后擬合模型變為：

使經過縮放變換的擬合曲線通過外場數據的部分采樣點，或者使用MATLAB進行擬合，通過求解待定系數或者擬合回歸的辦法，求得推導的外場曲線，解得縮放得到的最大擬合優度時的變化倍率k，平移量dT和擬合優度R2如表7所示，伸縮變換情況如圖4（a）所示。

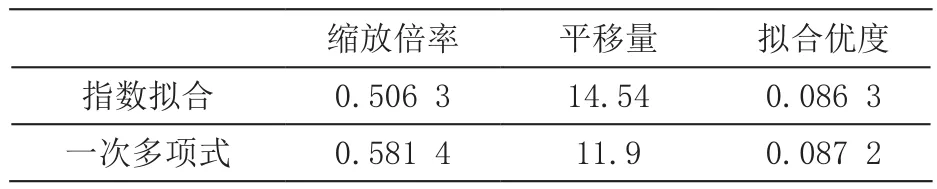
表7 指數擬合伸縮變換情況

對一次多項式擬合模型進行類似的縮放變換處理，得到最大擬合優度時的變化倍率k，平移量dT和擬合優度R2，如表7所示，相應的內外場變換情況如圖4（b）所示。

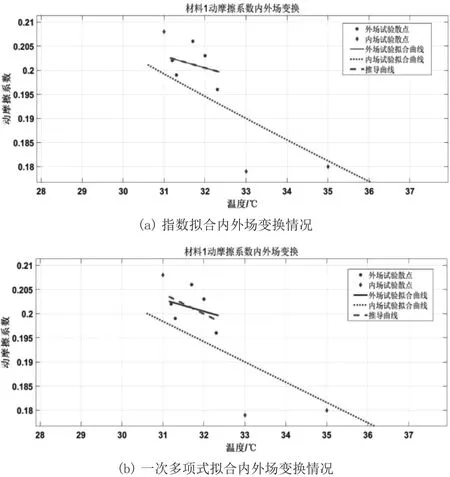
圖4 不同擬合方式的內外場變換情況

由表8可以直觀地看出，對內場擬合曲線采用縮放變換得到的推導曲線，其擬合優度與通過外場散點直接擬合得到的擬合曲線的擬合優度相等，擬合曲線的形狀比較相似，因此可認為這種縮放變換較為合理，成功將內場擬合曲線變換為外場擬合曲線。

表8 不同擬合方式的擬合優度

5.2 濕度作為影響動摩擦系數的自變量的表征方法

以濕度為自變量進行內外場試驗的相似性研究，采用縮放平移的方式對內場試驗擬合曲線進行變換，使經過縮放變換的擬合曲線通過外場數據的部分采樣點，或者使用MATLAB進行擬合，通過求解待定系數或者擬合回歸的辦法，求得推導的外場擬合曲線，解得縮放變換得到的曲線達到最大擬合優度時的變化倍率k，平移量dT和擬合優度R2如表9所示，縮放變換情況如圖5（a）和圖5（b）所示。

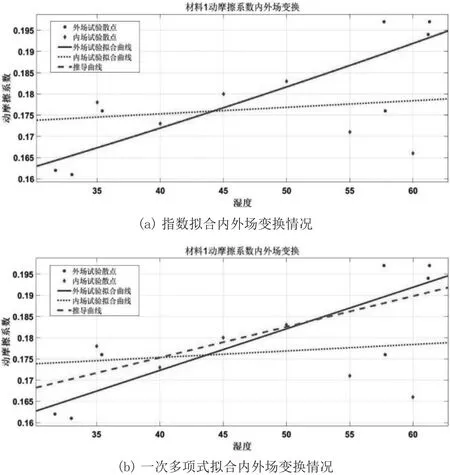
圖5 不同擬合方式的內外場變換情況

由表10可以直觀看出，根據縮放變換得到的曲線的擬合優度，指數擬合以及一次多項式擬合模型都有相對較好的擬合優度，擬合優度均高于0.7。將縮放變換得到的曲線與外場散點直接擬合得到的擬合曲線的擬合優度進行對比，采用一次多項式擬合模型時，二者比較接近，當采用指數擬合模型時，二者相等。因此可以認為這種縮放變換較為合理，成功將內場擬合曲線變換為外場擬合曲線。

6 小結

本文對剎車材料摩擦系數的內外場試驗進行了相似性研究，根據試驗結果可以得到以下結論：

表9 擬合模型縮放變換情況

表10 不同擬合方式的擬合優度

1）在摩擦系數的內外場試驗中，相同情況下，內場試驗得到的摩擦系數低于外場試驗下的摩擦系數，即內場試驗相較于外場試驗更“嚴苛”一些。

2）在以溫度作為自變量的相似性研究中，當采用指數擬合以及一次多項式擬合模型時，由內場擬合曲線經過縮放變換得到的推導曲線與直接由外場散點擬合得到的外場擬合曲線在擬合優度上比較接近；以濕度作為自變量時，采用縮放變換可以得到相同的效果。因此，這種縮放變換可以在一定程度上將內場擬合曲線變換為外場擬合曲線。