基于高斯過程回歸的船舶動力學模型辨識

陳 剛，王 威，霍 聰

(海軍工程大學 艦船與海洋學院，湖北 武漢 430033)

0 引言

隨著自主船舶技術的發展，船舶自主航行的安全尤為重要。當船舶執行避障或狹窄水域航行等高機動任務時，需要建立準確的動力學模型來預見船舶未來的運動狀態或軌跡，判斷控制策略是否有效或規劃路徑是否滿足船舶運動特性，并提前采取行動避免碰撞。高精度船舶數學模型可以提供準確的運動預測，對于船舶智能導航和控制器的設計至關重要。

船舶動力學模型辨識的目標是建立數學模型，在給定船舶運動狀態、推力和舵角作為輸入的情況下，生成船舶測量的運動狀態與模型預測運動狀態之間的最佳擬合。輸入和輸出之間的映射越準確，現實世界與模型之間的差距就越小。

目前，船舶動力學建模主要分為基于先驗模型的參數化建模和基于數據的非參數化建模。由于船舶表面不規則，水動力分析極其復雜，用第一原理建模非常困難，有許多先驗模型結構用于近似表達船舶動力學。其中一些模型廣泛用于水面船舶的動力學建模，如基于泰勒展開的三次Abkowitz 模型[1]和二次Norrbin 模型[2]。圍繞這些模型，參數化建模開展了大量的研究工作。諸如最小二乘法[3]、擴展卡爾曼濾波器 (EKF)[4]和最小二乘支持向量回歸(LSSVR)[5–6]等方法已用于船舶運動辨識。然而，這些方法都存在一些固有的缺點，如涉及參數過多，導致的多重共線性會使參數識別不準確，2 組不同的系數可以同樣好地預測某一特定工況，而它們在另一個工況中表現不佳，泛化性不足。許多方法被提出來克服參數漂移的影響[7]，最優截斷奇異值分解 (T-SVD)[8]和最優截斷最小二乘支持向量回歸(T-LSSVR)[9–11]被證明可以減少估計參數的不確定性。然而，這些方法是一種有偏估計，降低了水動力系數的準確性，從而降低了參數的方差，參數不確定性問題仍未完全解決。也有各種消除變量和簡化參數的模型[12–13]。然而，船舶的“真實”模型結構是未知的，確定船舶的模型結構一直是參數化建模實際應用中的一個難題。建立模型的目標是獲得準確的預測，不一定是獲得正確的水動力系數。

與參數化建模相比，非參數化建模幾乎不需要船舶模型結構的先驗信息，無需分析復雜的流體動力學，也可以獲得正確的輸入輸出映射。近年來，支持向量回歸（SVR）和局部加權學習（LWL）等機器學習方法被用于船舶動力學建模。廣義橢球基函數模糊神經網絡[14]用于模擬大型油輪的運動，但是，神經網絡的結構難以確定。v-SVM[15]被提出來建立操縱運動模型，并通過KVLCC2 船舶實驗數據進行驗證,它基于結構風險最小化來克服神經網絡容易過擬合但參數難以調整的缺點。一種新的基于局部加權學習（LWL）[16]的非參數辨識建模方法用于船舶動力學建模，它可以提供更高的建模精度，但存在計算復雜度高和計算時間長的缺點。核嶺回歸(KRR)[17–19]用于訓練具有多個隨機測試的模型，然而核嶺回歸需要執行網格搜索以進行超參數優化。總的來說，采用核函數的非參數建模避免了參數化建模需要了解模型結構的缺點，但仍然存在過擬合、超參數調整困難等問題。

高斯過程回歸（GPR）可以通過最大化邊際似然函數來自動優化超參數，還可以克服過擬合問題，它廣泛應用于機械臂[20]和賽車[21]的動力學建模。最近，它也被引入到船舶的動力學建模中，多輸出高斯過程被用來模擬集裝箱船運動[22]。薛[23]通過使用帶有人工噪聲的模擬數據，提出了一種考慮噪聲輸入高斯過程來進行船舶動力學建模，但目前僅限于模擬數據，沒有對實驗數據進行建模。

在本文研究中，基于高斯過程的非參數回歸被用于船舶動力學模型辨識，通過建立模型預測難以測量的船舶加速度。同時提出多步預測模型以提供船舶未來一段時間加速度、速度和位置信息。KVLCC2 的實驗數據用于驗證所提出方法的有效性。

1 船舶動力學參數模型和非參數模型

船舶動力學參數模型極其復雜，該模型包含輻射引起的附加質量、阻尼和恢復力。描述船舶動力學的參數化數學模型有很多，常用的運動方程[24]可以表示為：

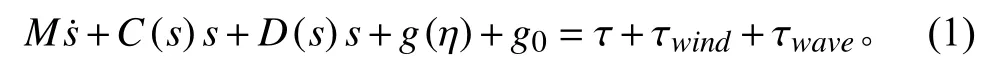
其中，船速s=[u,v,r]T與位置η=[x0,y0,ψ]T的 關系如圖1所示。

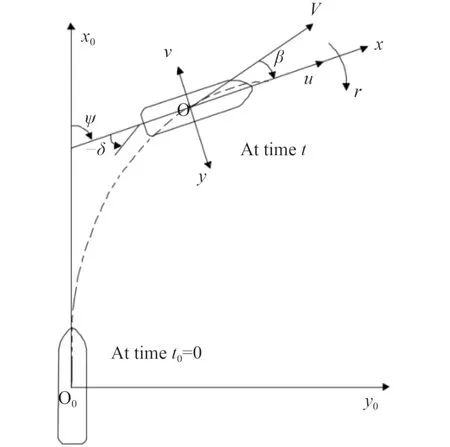
圖1 地球和船舶固定坐標系Fig.1 Earth and ship-fixed coordinate systems

當只考慮3 個自由度模型（縱向、搖擺和偏航）時，靜水恢復力和流體記憶效應可以忽略不計，不考慮外界風和流的影響，方程(1)可以簡化為：

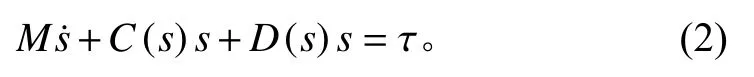
由于阻尼力D(s)的非常復雜，參數模型中通常使用二次或三次模型進行估計。根據參數化模型的表達形式，提出船舶動力學的非參數化表達如下：

其中：τ通常由推進器產生推力T和舵δ表示；s表示船舶運動速度；表示船舶運動速度，3 個自由度方向可以表示為：

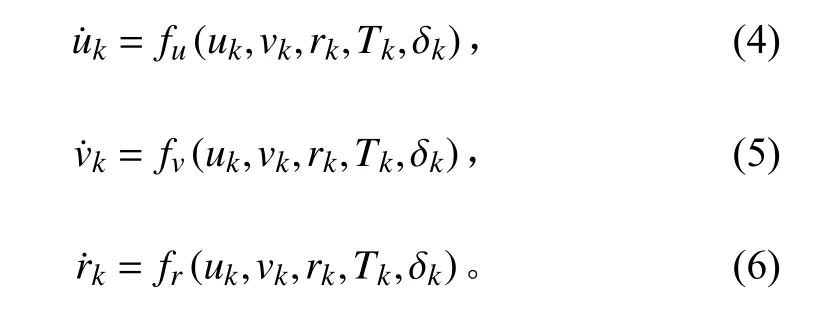
2 基于高斯過程回歸的非參數建模

2.1 高斯過程回歸

{(xi,yi)|i=1,···,n}是回歸的輸入和輸出，它們之間的關系可以表示為：

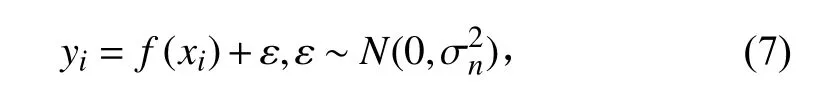
在高斯過程回歸[25]中，y和f(x?)的聯合分布為：

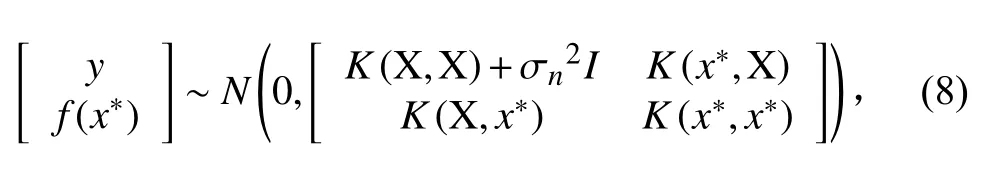
f(x?)的預測值為：

通常采用平方指數協方差函數作為核函數：

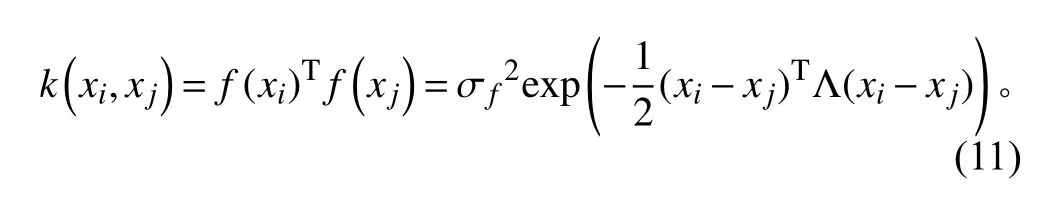
其中，?f和Λ是核函數的超參數。使用共軛梯度或擬牛頓法算法對邊際似然函數可對超參數進行優化。

2.2 船舶運動狀態多步預測模型

在控制船舶時，通常希望在執行控制命令后預測未來k步船舶的運動響應。一個簡單的方法是按順序應用單步預測模型k次。在傳感器信號丟失的情況下，多步預測模型用于提供未來一段時間的軌跡估計。

對于船舶動力學模型，多步預測模型的主要輸入為：初始速度狀態(u0,v0,r0)和接下來k步中的舵角控制命令(δ0,δ1,δ2,...δk?1)。為了簡化模型，螺旋槳速度T通常可以被視為常數而不是輸入變量。輸出是船舶在接下來k步中的加速度，通過歐拉積分可以得速度和船舶的位置，多步預測模型的輸入和輸出如圖2 所示。

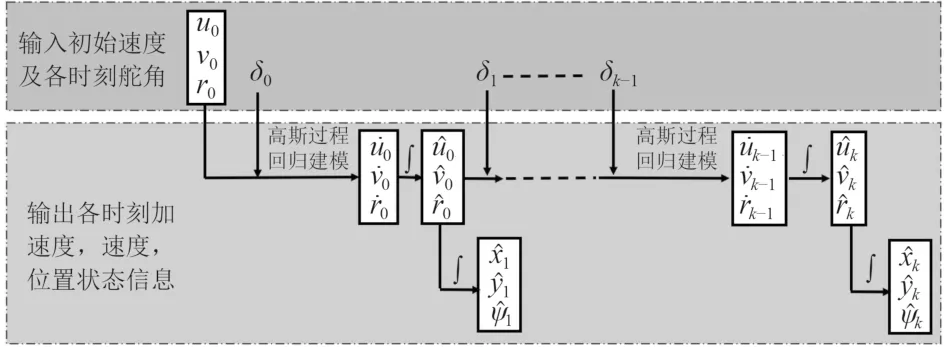
圖2 多步預測模型的輸入和輸出Fig.2 The inputs and outputs of multi-step prediction model

多步預測模型容易受到誤差累積問題的影響，過去的誤差會傳播到未來的預測中。因此，有必要盡可能提高單步預測的準確性。

3 KVCLL2 船舶動力學辨識

3.1 實驗船模型和數據集

自由航行試驗是船舶動力學識別的常用方法。這種方法只需要測量船舶的位置和速度等狀態信息，不需要測量力。此外，它還可以應用于全尺寸船舶以避免規模效應。KVLCC2 是一艘大型油輪，在國際上已被用作驗證船舶模型辨識方法的基準船型。本文使用的試驗數據來自在德國漢堡水箱（HSVA）進行的KVLCC2 模型自由航行試驗。KVLCC2 模型的主要參數詳見表1。試驗開展了一系列Z 形測試，所有的數據用在20 Hz 的采樣率采集。此研究中所用的試驗數據見表2。

表1 KVLCC2 型號參數及尺寸Tab.1 Parameters and dimensions of the KVLCC2 model

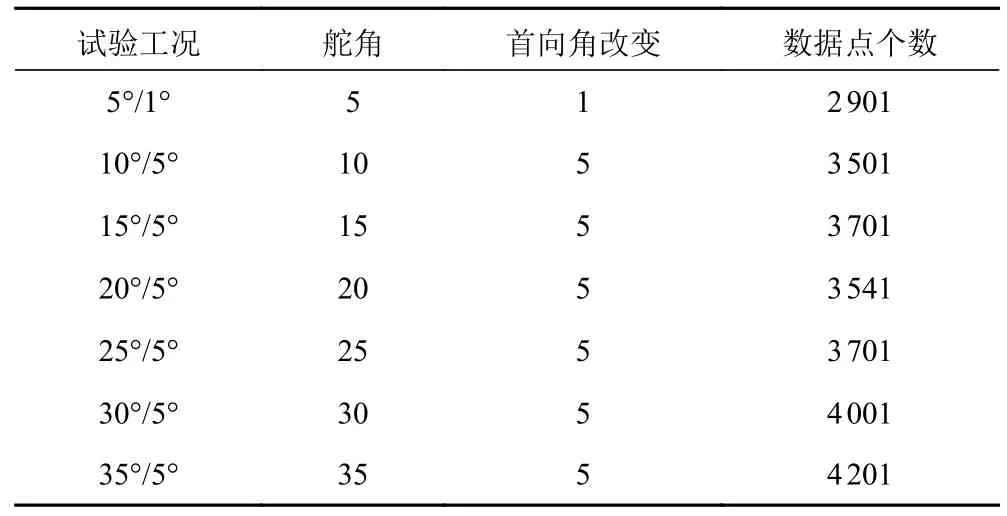
表2 KVLCC2 試驗數據Tab.2 Test data of the KVLCC2 model

3.2 基于高斯過程回歸的船舶動力學辨識

傳統的機動運動預測需要預測超調角和戰術直徑。然而，在規劃路線或控制船舶避開障礙物時，操作員更需要知道在執行完一段控制命令后預測的船舶狀態響應或軌跡是否與實際情況一致。因此，必須確保辨識中的控制指令和試驗中的控制命令始終相同。基于高斯過程回歸的非參數回歸被用于船舶動力學建模。歷史的控制命令和運動響應數據用于訓練模型。訓練后的模型可以準確預測未來任何控制命令的運動響應。

非參數建模主要適用于插值預測，為了學習一個“好”的模型，訓練數據必須覆蓋船舶狀態空間較大范圍。因此，使用5°/1°，10°/5°，20°/5°，30°/5°，35°/5°之字形測試來訓練模型，數據幾乎覆蓋了舵角的輸入空間。數據太多會使計算變慢，每間隔12 個點選1 個進入訓練集，訓練集中共有1 512 個訓練點。25°/5°之字形測試作為驗證集，預測間隔為0.05 s。

通常，加速度無法測量或者測量不準確，可以直接用速度差分代替加速度。雖然會放大噪聲，使加速度不可靠，但不影響模型預測結果，因為高斯過程回歸可以應用于噪聲數據回歸，辨識得到準確的加速度值。25°/5°Z 形試驗加速度的3 700 步預測值和試驗值如圖3 所示。可以發現，試驗中速度差分得到的加速度具有較強的振蕩性，通過高斯過程回歸可以很好地得到準確的加速度預測值。

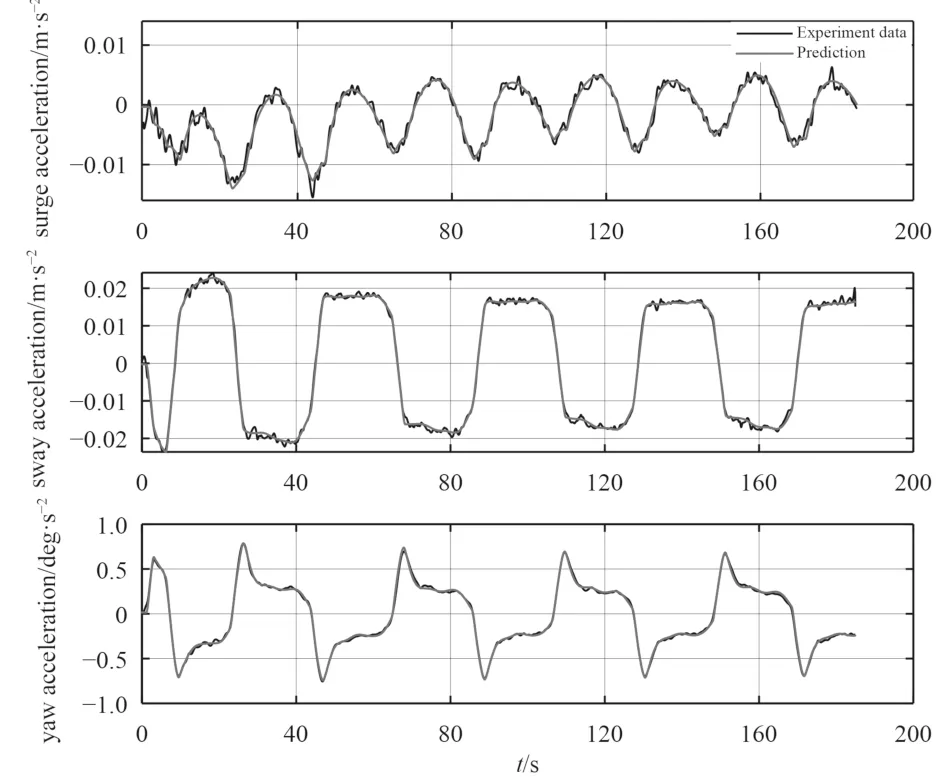
圖3 25°/5°Z 形運動中的加速度3 700 步預測Fig.3 3 700 steps prediction of acceleration in 25°/5° zigzag maneuver

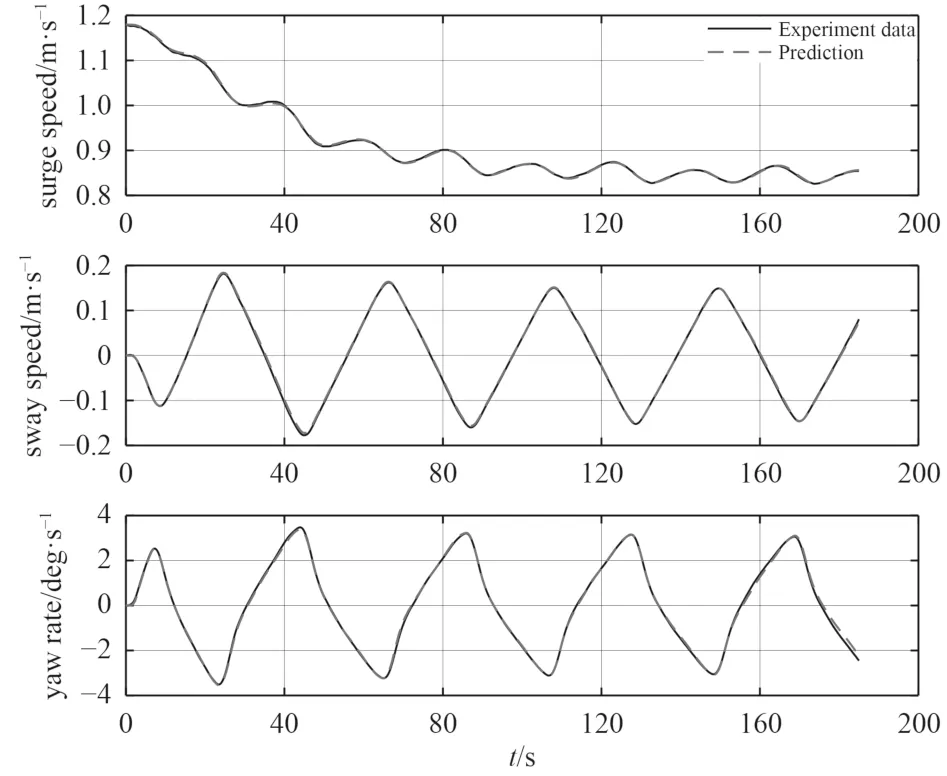
圖4 25°/5°Z 形運動中的速度3 700 步預測Fig.4 3 700 steps prediction of speed in 25°/5° zigzag maneuver

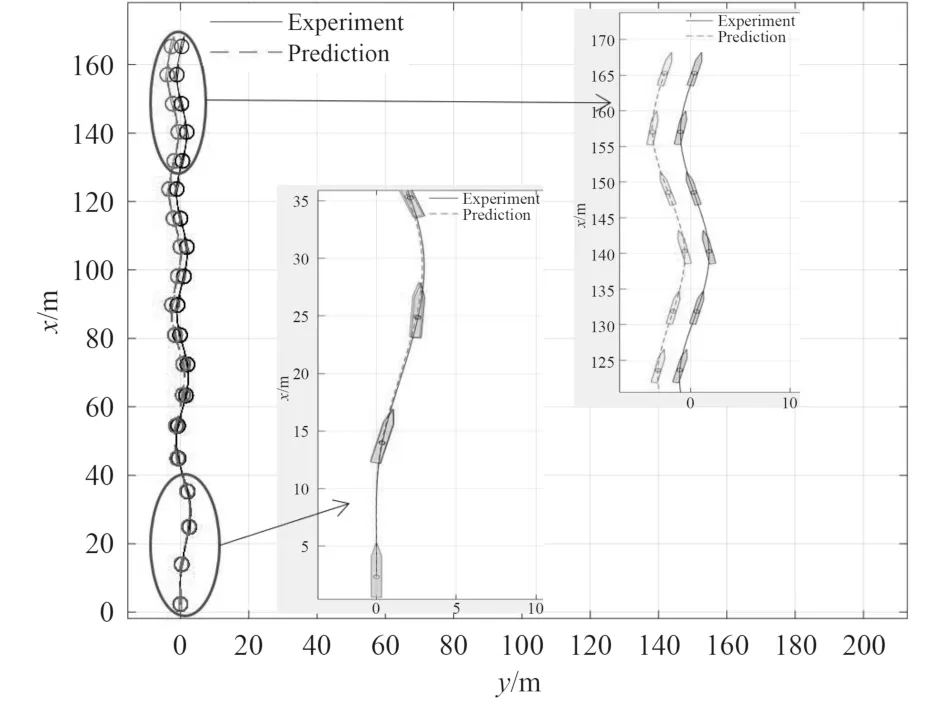
圖5 25°/5°Z 形運動中的軌跡3 700 步預測Fig.5 3 700 steps prediction of position in 25°/5° zigzag maneuver

該模型訓練時間為87 s，然而，訓練時間并不重要，因為模型只需要離線訓練一次，相比之下，預測時間更為重要，預測時間越短，可實現控制頻率越高。選擇不同的起始點來進行多步預測，比較預測時間和預測精度。如表3 所示，一步預測準確率高，預測所需時間短。隨著預測步數的增加，預測時間會在一定程度上增加，累積誤差也會增加，歐拉積分方法會導致誤差隨著時間的推移而增加。但模型仍能保持較高的預測精度，100 步的位置跟蹤誤差為0.013 m，1 000步的位置跟蹤誤差為0.599 m。

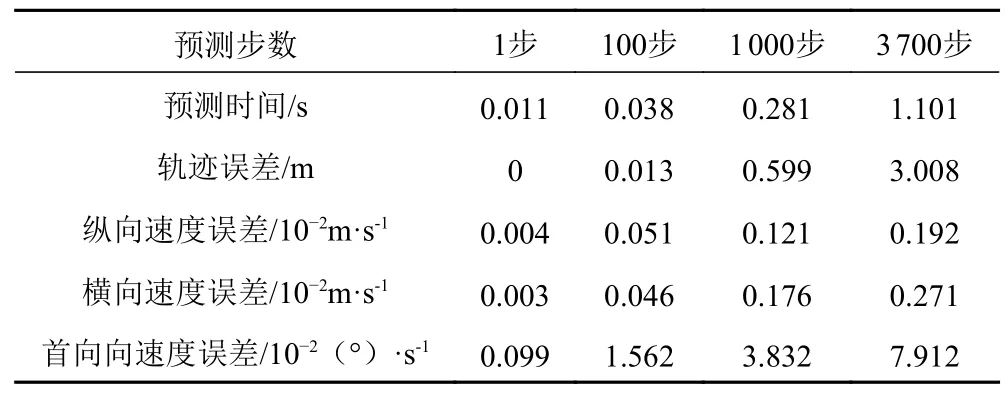
表3 25°/5°Z 形試驗多步預測RMSE 的精度Tab.3 Multi-step prediction accuracy assessed by the RMSE of the 25°/5° zigzag test

在預測船舶運動響應時，通常假設控制輸入舵角在預測區間內恒定或緩慢變化，因此時間間隔應盡可能小。在大區間預測中，舵角變化較大時，預測精度會降低。因此，為了實現多步高精度預測，應盡量選取較小的區間。

4 結語

基于高斯過程的非參數回歸被用于船舶的動力學辨識，KVLCC2 的試驗數據用于驗證所提方法的有效性。結果表明，通過高斯過程回歸辨識得到的模型可以準確預測船舶未來一段時間的運動響應。在傳感器信號丟失的情況下，模型未來仍能提供準確的船舶加速度、速度和位置信息，1 000 步的位置預測誤差為0.599 m。

基于高斯過程回歸的船舶動力學建模模型的優點可以概括為：1）與參數辨識不同，基于高斯過程回歸的模型不需要知道船舶動力學的先驗模型結構，可以得到準確的從輸入到輸出的映射；2）與LSSVR 等其他黑盒識別相比，該模型可以通過最大化邊際似然來自動調整超參數，減少因超參數不準確而導致的預測精度損失；3）該模型可以應用于噪聲數據而不會過擬合，它可以準確估計難以測量的加速度。

但是，所提出方法的許多問題還需要進一步研究：對于非參數識別，訓練數據必須覆蓋轉向角的輸入空間，回轉的預測和隨機舵運動預測是否需要改變訓練集有待進一步的實驗數據驗證。同時數據量越大，預測精度越高，但訓練時間會更長甚至無法計算。未來的研究可以嘗試將局部高斯過程回歸應用于大數據船舶動力學建模。