大洋勘探船月池阻力特性研究

李文娟，陶延武，羊 衛，張海彬

(1.江蘇科技大學 海洋裝備研究院，江蘇 鎮江 212003；2.中國船舶及海洋工程設計研究院，上海 200011)

0 引言

勘探船是礦產、油氣資源調查以及海洋科學研究的重要裝備，相比于調查船和科考船，勘探船具有進行海底深部鉆探取樣的能力，可以對海底礦產的組成以及儲量進行深入評估。從國內外深海礦區勘探需求來看，大洋勘探船具有明顯的市場應用前景。

月池是貫穿船底和甲板的開口，以便船上的設備進入水下進行操作。為滿足鉆探需要，勘探船通常在船中位置布置較大的月池，另外為方便ROV 以及其他探測設備的收放還會設置較小的月池。月池的存在對船舶的穩性和強度不利，使水動力性能與普通船舶有較大的差異，月池內流體的復雜運動會導致勘探船航行阻力、耐波性能復雜的多。

Gaillarde 和Cotteleer[1]通過實驗研究了抑制月池內運動不同裝置的試驗，以減少月池內的自由表面高度變化。還對沿船體深度方向的截面形狀的月池進行研究，減少月池內水的運動。Larsson 等[2]將船舶的整體阻力分為2 個部分：波浪阻力和粘性阻力。在這2 個阻力部分中，帶有月池的鉆井船對波浪阻力影響不大，但會影響粘性壓阻力，這主要是由于月池壓力不平衡產生的。Molin[3]采用線性化勢流理論，得出了二維和三維月池的活塞模式和晃動模式的固有頻率的理論公式以及活塞和晃蕩模式的自由表面形狀公式。月池的共振振蕩是由船舶航行時在月池的上游底端形成的漩渦引發的。Veer 等[4]對具有不同長寬比月池的鉆井船進行了模型試驗，并研究了月池形狀與月池增阻之間的關系，分析了月池吃水寬度比與月池內自由表面高度的變化的關系。Tholen[5]試驗研究了長寬比Lm/Bm=2 的月池，其研究的焦點在于減阻裝置減少附加的船舶瞬態阻力。在早期的設計階段，主要通過模型試驗與已有的船型數據相結合得出帶月池船舶的阻力曲線。但是這種方法要準確估計月池的增阻大小仍然很困難，船體以及月池通常變化很大，而可用的數據比較有限，無法實現阻力曲線的準確預測。Sivabalan.P[6]通過CFD 方法對一艘帶月池的鉆井船在低航速下阻力特性進行了研究，傅汝德數范圍為0.019 6～0.157，月池為矩形月池，發現航速最高時月池增阻約為25%。

本文針對帶有月池的勘探船進行航行阻力研究，通過CFD 方法開展勘探船靜水阻力預報研究，考慮直立型首和球鼻型首2 種船型以及無月池、首月池和雙月池3 種方案組合，分析各船型方案的總阻力以及月池增阻情況，將船體阻力按照傅汝德分類法分為摩擦阻力和剩余阻力分量，分別探究不同船型及月池方案的摩擦阻力和剩余阻力分量的規律。

1 計算模型

1.1 模型主尺度

研究對象為兩大類船型，分別為球鼻型首船型和直立型首船型，兩船型的主尺度相同。兩船型的主尺度見表1。

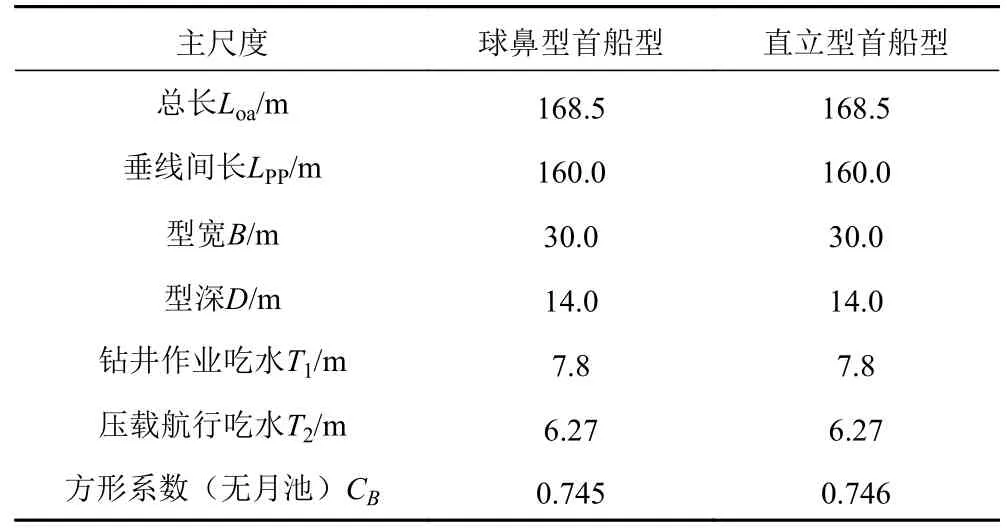
表1 船舶主尺度Tab.1 Main dimensions of the two type ships

1.2 月池布置及尺寸

含2 種類型的月池，后月池截面為正方形，后月池為截面為正方形，首月池為“凸”字形，凸起方向指向船體尾部。后月池尺度相對較小，設計吃水和壓載航行狀態時的長度吃水比分別為0.54 和0.67。首月池主體部分截面為正方形，后端設置矩形截面凹槽。設計吃水和壓載航行狀態時，首月池主體部分的長度吃水比分別為1.08 和1.34。水深吃水比是月池水動力特性的重要影響因素，對月池的增阻作用有較大的影響。月池布置及尺寸見圖1、圖2 及表2、表3。

表2 后月池尺寸Tab.2 Size of after moonpool

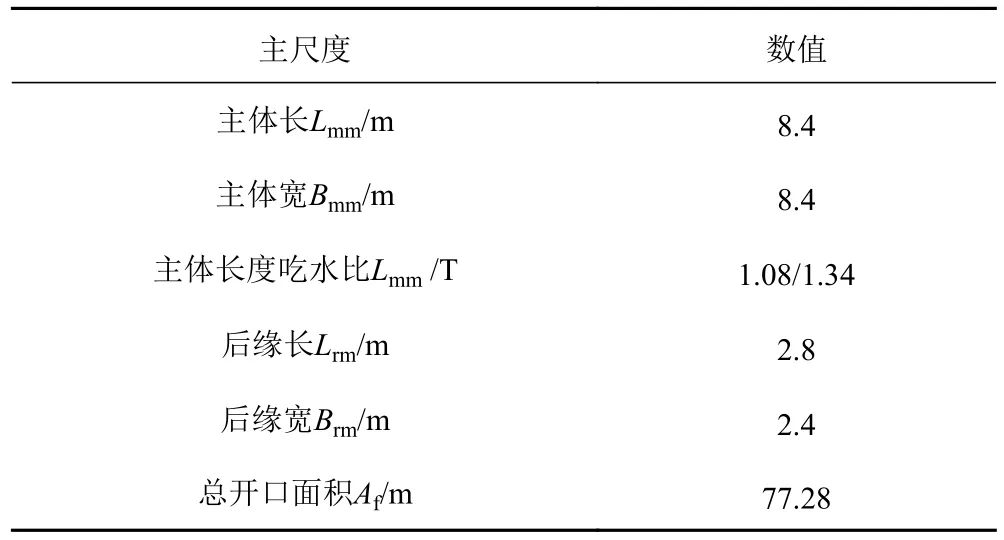
表3 首月池尺寸Tab.3 Size of bow moonpool

圖1 船型三維圖Fig.1 3D view of ship shape

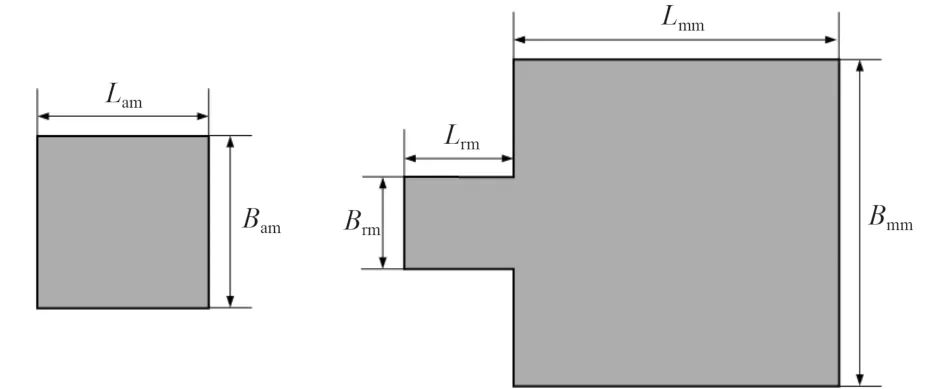
圖2 月池尺寸示意圖Fig.2 Sizes of moonpools

2 大洋勘探船月池阻力數值模擬及分析

2.1 計算工況

考慮到勘探船的作業吃水有一定變化，月池的長度吃水比(Lm/T)也相應發生變化，可能導致月池內主導的振蕩模式發生轉變，所以計算時選擇2 種吃水狀態，即設計吃水狀態（鉆井作業）和壓載航行狀態，LC1代表設計吃水，LC2代表壓載吃水。為覆蓋勘探船可能的服務航速，計算時取航速范圍為7～15 kn，間隔為1 kn。計算工況如表4 所示。

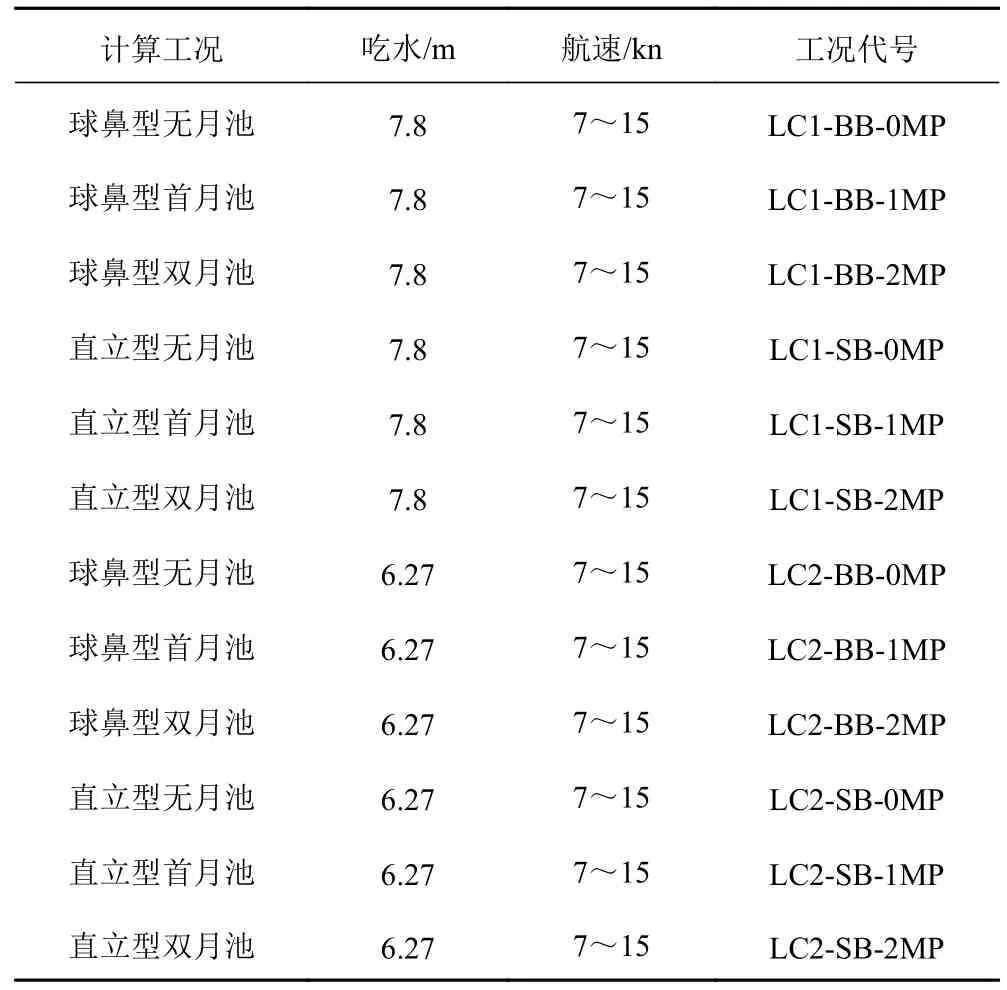
表4 計算工況Tab.4 Calculation conditions

2.2 計算方案

數值模擬使用FINE/Marine 軟件，其采用了粘性ISIS-CFD 求解器。

1）計算域及邊界條件

采用半模計算，計算域寬度為2LPP，計算域長度為5.5LPP，船后長度為3.5LPP，船前長度為1LPP，計算域高度為2LPP，空氣域高度為0.5LPP，水域高度為1.5LPP。計算域與船體中縱剖面重合面為對稱平面，上部和下部為壓力出口，計算域其余邊界為遠場邊界。

2）計算時間步長設置

ITTC (75-03-02-04,2014) 推薦的計算船舶阻力的時間步長與船舶的航速以及船長有關，計算時間步長取為：

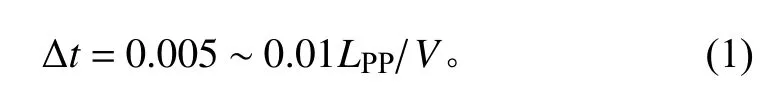
式中：LPP為船舶的垂線間長，V為對應的航速。

計算時間步長根據航速調整，各計算工況的計算時間步長具體如表5 所示。

表5 各工況的計算時間步長Tab.5 Computation time steps of different conditions

3）平均阻力提取方法

由于阻力隨時間波動，尤其在月池長度較大的時候，提取阻力時以計算結果的平穩段時間平均值作為平均阻力。在阻力出現明顯周期性波動時，截取時間段要足夠長，截取時間盡量等于整數個周期，以減小數據處理帶來的誤差。

4）網格收斂性驗證

為進一步驗證計算結果與網格數的獨立性，針對球鼻型首雙月池模型，設計吃水，實船航速Vs=7 kn（LC1-BB-2MP-V7）工況采用3 套網格劃分方案進行驗證，網格數分別為193 萬、237 萬和369 萬，方案2和方案3 的結果接近，網格數為237 萬時計算結果在誤差允許范圍內可以接受。因此帶月池工況網格劃分方案采用與方案2 類似的網格加密方法。

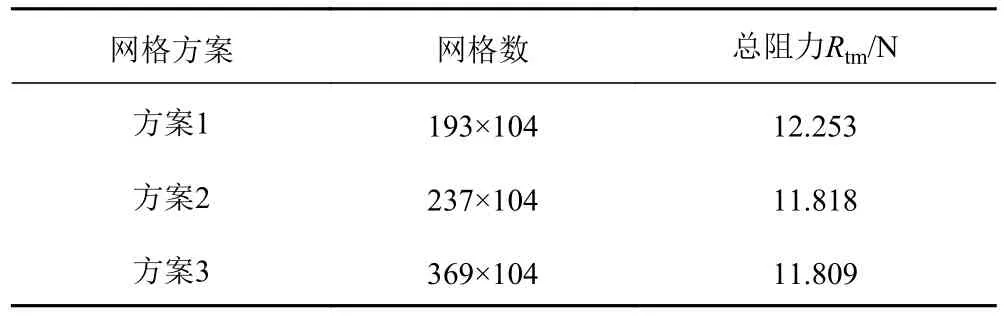
表6 三種網格方案計算結果對比Tab.6 Comparison of calculation results of three grid schemes

2.3 計算結果

2.3.1 球鼻首船型設計吃水航行阻力

圖7 為球鼻首船型設計吃水阻力曲線，按照傅汝德分類法的思想，將總阻力Rt分為摩擦阻力Rf和剩余阻力Rr。可以看出單月池和雙月池布置的總阻力差別不大，無月池、單月池和雙月池布置的摩擦阻力接近，而單月池和雙月池布置的剩余阻力要比單月池船型的大，這也是導致單月池和雙月池布置的總阻力比無月池船型總阻力大的主要原因。

圖7 球鼻首船型設計吃水阻力曲線Fig.7 Resistance curve of bulb bow at designed draft

圖8 為球鼻首船型壓載吃水阻力曲線。結合設計吃水結果來看，發現吃水減小后，單月池和雙月池布置的總阻力差別增大，主要是由剩余阻力分量引起的。由于總的濕面積減小，在相同的船底剪切濕面積損失情況下，3 種布置的摩擦阻力的差別也稍有增大。

圖8 球鼻首船型壓載吃水阻力曲線Fig.8 Resistance curve of bulb bow at ballast draft

2.3.3 直立首船型設計吃水航行阻力

圖9 為直立首船型設計吃水阻力曲線。單月池和雙月池布置的總阻力以及摩擦阻力和剩余阻力分量差別均不大。相比于無月池，帶月池布置（單月池和雙月池型）的摩擦阻力有一定降低，而剩余阻力增加較大，導致總阻力有一定增加。

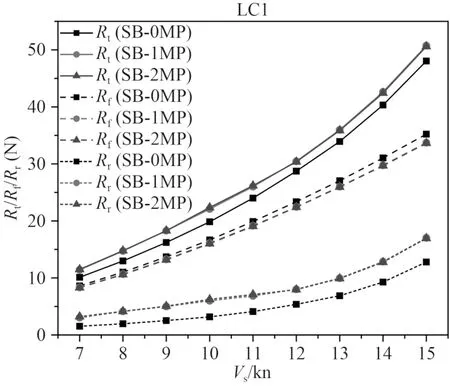
圖9 直立首船型設計吃水阻力曲線Fig.9 Resistance curve of straight bow at designed draft

2.3.4 直立首船型壓載吃水航行阻力

圖10 為直立首船型壓載吃水阻力曲線。壓載吃水狀態3 種布置的各阻力成分均有明顯差別。雙月池布置的總阻力和剩余阻力最大，單月池次之，無月池最小。而摩擦阻力成分與此相反，但單月池和雙月池的摩擦阻力差別并不明顯。

圖10 直立首船型壓載吃水阻力曲線Fig.10 Resistance curve of straight bow at ballast draft

2.4 計算結果分析

通過對不同船型以及月池布置方案阻力計算結果對比可以發現：

1）對于相同的月池布置方案的船型，無論是在設計吃水還是在壓載吃水狀態，球鼻首船型的總阻力均大于直立型船型。設計航速設計吃水狀態，球鼻首船型的無月池、單月池和雙月池方案的阻力比直立型船型分別大5.4%，6.6%和7.1%；在設計航速壓載吃水狀態，球鼻首船型的無月池、單月池和雙月池方案的阻力比直立型船型分別大8.7%，10.0%和9.8%。兩船型的總阻力對比如圖11 所示。

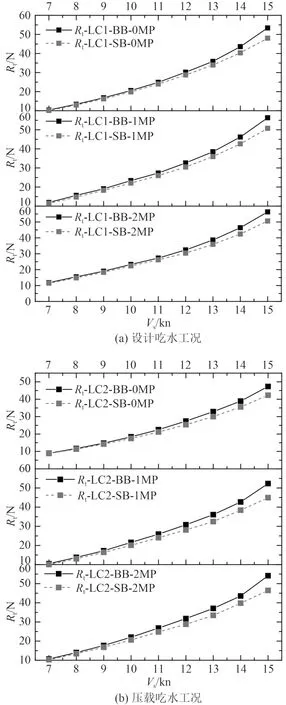
圖11 兩船型阻力對比Fig.11 Comparison of resistance of two different ship types

2）通過對單月池和雙月池方案對比發現：在設計吃水狀態下單月池和雙月池方案的總阻力差別不大，而在壓載吃水狀態雙月池方案總阻力比單月池方案稍大一些。具體來看，設計航速設計吃水狀態和壓載吃水狀態，球鼻型雙月池阻力比單月池阻力分別增大3.1%和2.7%，直立型雙月池阻力比單月池阻力分別增大3.1%和2.9%。

本次大賽的16個作品經過賽前抽簽，分成四組進行決賽。上海圖書館副館長林峻，上海師范大學謝晉影視藝術學院播音主持藝術專業主任高祥榮，上海音樂學院歌劇指導專業、音樂教育專業碩士生導師張繼紅擔任大賽評委，并為各位選手的表演進行精彩點評。

3）月池形式的變化對阻力的影響主要體現在剩余阻力增加上，另外月池的存在會減小摩擦阻力。

4）吃水狀態對月池產生的剩余阻力影響較大，進而影響不同船型的總阻力大小。

通過提取帶月池勘探船與不帶月池勘探船的阻力差，可以得到月池增阻。本文將總阻力、剩余阻力、摩擦阻力分別提取得到相應的月池增阻。2 種船首以及2 種吃水狀態下單月池和雙月池方案的月池增阻如圖12 和圖13 所示。

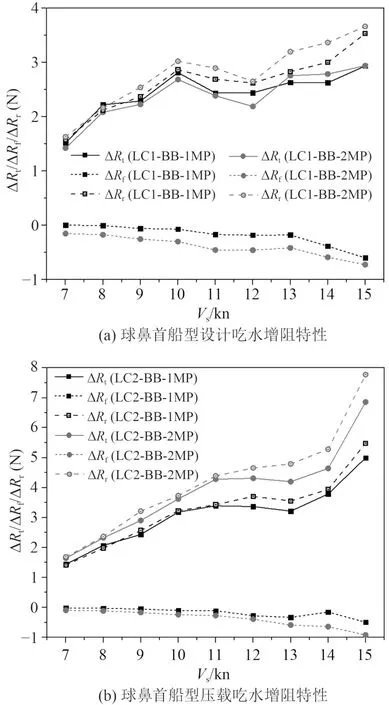
圖12 球鼻首船型月池增阻曲線Fig.12 Curve of added resistance of moonpool of bulb bow

圖13 直立首船型月池增阻曲線Fig.13 Curve of added resistance of moonpool of straight bow

可以看出，低航速時，月池增阻隨航速增加，而航速在11～13 kn 附近出現拐點，月池增阻呈下降或平穩趨勢，航速大于13 kn 后，增阻趨勢隨吃水及船型的不同而呈現不同的趨勢。

無論何種船型或吃水狀態，月池的存在導致摩擦增阻為負值，即月池會降低船體的摩擦阻力。雙月池方案摩擦阻力減小程度更大一些。

月池的剩余阻力增量為正值，摩擦阻力增量為負值，摩擦阻力的增量的絕對值要比剩余阻力的增量絕對值小，兩者疊加后的總阻力增量為正值。高航速下摩擦阻力的增量的絕對值約為剩余阻力的增量絕對值的1/4 左右。

3 結語

對不同船型以及月池布置方案阻力數值計算結果對比可以發現：

1）對于相同的月池布置方案的船型，無論是在設計吃水還是在壓載吃水狀態，球鼻首船型的總阻力均大于直立型船型。

2）通過對單月池和雙月池方案對比發現：在設計吃水狀態下單月池和雙月池方案的總阻力差別不大，而在壓載吃水狀態雙月池方案總阻力比單月池方案稍大一些。

3）低航速時，月池增阻隨航速增加，而航速在上升到一定值附近會出現拐點，月池增阻呈下降或平穩趨勢，航速繼續增大后，增阻趨勢會隨吃水及船型的不同而呈現不同的趨勢，但無論何種船型或吃水狀態，月池的存在導致摩擦增阻為負值，即月池會降低船體的摩擦阻力。雙月池方案摩擦阻力減小程度更大一些。