基于信號的鋰離子電池熱失控故障早期檢測

薛金花，王德順,2，李碩瑋，杜凈彩

(1.中國電力科學研究院有限公司，江蘇南京 210003；2.東南大學自動化學院，江蘇南京 210096；3.北京交通大學電氣工程學院，北京 100044)

鋰離子電池具有能量密度高、工作溫度范圍寬、壽命長等優點，在儲能領域被廣泛應用。為滿足儲能系統對能量和功率級別的要求，通常需要采取串并聯成組方式進行使用[1]。但串并聯成組方式難以實現每個單體狀態的精確估計，電、熱濫用或運行環境惡劣等原因可能引起電池組單體內部結構發生改變進而導致熱失控事故，因此需要盡早實現對電池潛在故障的準確檢測，及時停止電池濫用，避免出現危險情況[2]。

電池故障診斷方法可分為基于模型、基于信號、基于知識三類。Ouyang 等[3]提出一種利用遞推最小二乘法估計等效電路模型均差模型參數的微短路檢測方法，將電池單體的參數與設定的閾值比較以檢測內部短路故障，基于模型的方法可以準確辨識出電池故障，但模型參數辨識需要特定工況，實際運行工況及數據精度難以建立準確的電池故障模型；Sun 等[4]使用香農熵對小波變換后的電池電壓進行分析并準確檢測出電池連接故障，基于信號的方法無需建立模型，但各種信號分解方法的計算量不同，不同特征對測量噪聲敏感度不同，亟須提出可靠且可在線應用的信號處理、特征提取方法；文獻[5]利用故障樹定性分析電池系統故障原因，再通過小波分析提取故障診斷特征量，建立電池系統故障診斷神經網絡，從而實現電池系統的故障診斷，基于知識的方法需要大量準確標注故障類型的數據，且由于部分故障沒有被完全理解，基于知識的方法需要更有效的規則來精確檢測每個故障。

綜上，現有的故障診斷方法均存在一定的局限性，如模型參數難以辨識，缺少可靠且可在線應用的信號處理、特征提取方法，需要大量準確標注故障類型的數據等，難以基于少量實際運行數據在故障早期階段快速檢測出故障。本文提出一種基于信號分解的故障檢測方法，將經驗模態分解與相關系數相結合在線實現故障的早期檢測，與小波變換等信號分解方法相比，經驗模態分解計算量較小且無需選取小波基等參數，皮爾遜相關系數適合在線應用[6]，在一定程度上改進了基于信號方法難以在線應用的缺點，更早地實現電池故障檢測。

1 鋰離子電池熱失控過程分析

本文案例一熱失控數據源于某鋰離子電池組實際運行工況數據，該電池組充電截止電壓為4.26 V，在電池組熱失控前9 個充電段的最高充電電壓均超出4.25 V，熱失控前7 日最高溫度為33 ℃，未超出正常溫度上限，由此判斷熱失控前電池組電壓溫度未出現異常。圖1、圖2 分別展示了電池組熱失控前最后一個充放電循環與熱失控過程電壓、溫度曲線，充電制式為分段式恒流充電，充電倍率分別為0.45C、0.3C和0.1C。充電與靜置階段電池組溫度傳感器測量到的溫度均穩定在50 ℃以下，未超過正常溫度上限，電壓較為穩定未出現異常。

圖1 熱失控過程電池組單體電壓曲線

圖2 熱失控過程電池組溫度曲線圖

放電段熱失控過程分析如下：

(1)在第883 采樣點A 號單體電壓開始呈現持續下降趨勢，此時溫度正常；

(2)在第894 采樣點前，所有傳感器的采集時間間隔為10 s，第894 個采樣點后降至1 s，推測此時BMS 檢測出故障，此時A 號單體電壓下降較為明顯，溫度正常；

(3)在第907 采樣點A 號單體電壓上升到5 V，遠超鋰離子電池正常電壓上限4.3 V，原因是采集電路電壓上限為5 V，BMS 選擇5 V 作為故障狀態標志值，此時BMS 檢測出A 號單體故障，溫度正常；

(4)在第919 采樣點與A 號單體相鄰的兩個溫度傳感器溫度上升，在第929 采樣點其中一個溫度傳感器升至最高溫度87 ℃，電池正常工作溫度不超過50 ℃，綜合之后的電壓表現推測此時電池發生熱失控。

從BMS 檢測出故障(894 采樣點)到熱失控(929 采樣點)經歷了大約35 s，35 s 的時間間隔難以采取有效措施抑制電池熱失控，因此有必要實現故障快速檢測。

本文研究思路如圖3 所示。基于以上分析，熱失控發生時電壓異常表現早于溫度異常表現，因此本文主要對電池電壓進行分析。由于熱失控事故發生在放電段，放電段工況不穩定電壓波動較為明顯，直接采用相關系數法難以獲得準確的結果，因此采用經驗模態分解(empirical mode decomposition,EMD)對放電段電壓數據進行分解得到穩態分量，再計算相關系數，通過K-means 算法自動辨識故障單體，實現鋰離子電池故障早期檢測。

圖3 基于信號分解的鋰離子電池故障檢測流程圖

2 基于信號分解的鋰離子電池故障檢測原理

2.1 經驗模態分解

在運行工況中放電段工況不穩定，電池組各單體電壓隨電流變化而波動，EMD 作為一種自適應信號分解方法，無需設定參數即可實現原始信號的分解，本文采用EMD 算法對放電段電壓信號進行分解。

EMD 將原始電壓信號分解得到不同特征尺度的本征模函數(IMF)，IMF 需滿足以下條件[7]：

(1)IMF 的極值點和過零點的個數差小于等于1；

(2)局部極小值和局部極大值產生的兩條包絡線之間所有點的均值都為0。

具體步驟[7]為：

(1)獲取初始信號x(t)的所有局部極值點，然后通過三次樣條線分別將所有極大值和極小值連成上、下兩條不同的包絡線rmax(t)和rmin(t)；

(2)上、下包絡線之間的任一時刻均值記為μ1，從時域信號中減去均值，得到新的時域信號，y1(t)=x(t)-μ1；

(3)判斷y1(t)是否滿足IMF 條件，若滿足則是第一個IMF，若不滿足則y1(t)重復進行步驟(1)～(2)的運算，直到滿足IMF 兩個條件；

(4)計算剩余項q1(t)=x(t)-y1(t)，并作為新的初始信號，重復步驟(1)～(2)，將原始信號分解為n個IMF 分量，直到滿足給定的終止條件，得到式(1)：

式中：x(t)為原始信號；qn(t)為殘余分量，表示信號的平均趨勢，信號從高頻到低頻的不同分量用yi(t)表示。

2.2 皮爾遜相關系數

皮爾遜相關系數是度量兩個變量X和Y之間線性關系程度的量，如式(2)所示：

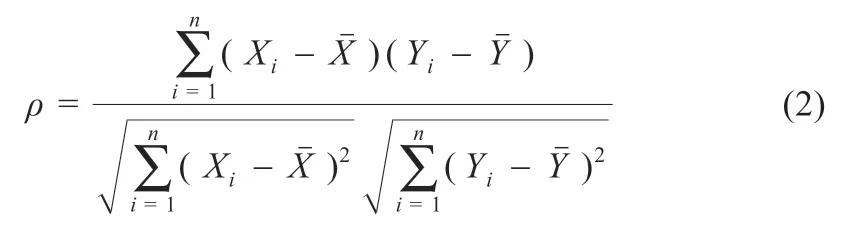
3 基于EMD 與相關系數的故障檢測方法

對電池組各單體放電段電壓進行EMD 分解，EMD 可以將原始信號分解為若干個不同頻率的IMF，本文將最低頻分量定義為穩態分量并用于故障檢測。

由于BMS 在第894 個采樣點檢測出故障，為實現故障早期檢測，本文選取第424(放電開始)～891 個采樣點電壓數據，第891 個采樣點早于BMS 第894 個采樣點26 s，分解電壓后得到的電壓穩態分量如圖4 所示。A 號單體電壓穩態分量在第883 個采樣點開始出現電壓跌落的現象，與原始電壓變化趨勢相同。在實際應用時，每當單體電壓更新，即獲取到下一采樣點單體電壓，使用EMD 分解更新后的電壓序列。

圖4 第424～891個采樣點原始曲線經驗模態分解后穩態分量曲線

在同一工況下，電池組內不同單體的電壓響應大致相似，以某只單體的電壓曲線為參考基準，將該參考基準電池記為B 號單體，將B 號單體電壓分解后得到的穩態分量作為參考分量，求取其余單體的穩態分量與參考分量之間的相關系數，若只有B 號單體出現電壓跌落，則所求得的所有相關系數絕對值均應較小，接近于0；若其它個別單體出現故障，則故障單體的相關系數絕對值應較小，接近于0。

此外，運行工況中電壓采集誤差等原因會造成偶然的電壓數據異常波動，為更準確地篩選出電池組中故障單體，采用滑動窗口的方法來避免電壓波動所導致的誤判。選取時間序列中一定窗口寬度的電壓穩態分量作為子序列，本文選取窗口寬度為20，計算每個窗口內B 號單體電壓穩態分量子序列與其余單體電壓穩態分量子序列之間的相關系數，結果如圖5(a)所示。根據2.2 節結論，當相關系數低于0.4 時，兩個子序列的相關程度較弱，因此本文將相關系數的閾值設置為0.4。遵循故障單體個數為少數且故障單體極大可能影響相鄰兩個串聯單體的原則，若低于0.4 且異常單體個數小于4，則認定異常單體電壓出現異常，可能發生熱失控。本案例中A 號單體與B 號單體的相關系數最終下降到0.321，而其他單體與B 號單體的相關系數較大，此時本方法檢測出A 號單體電壓異常。本文將熱失控前的故障報警時間作為量化指標來評價方法的優越性，BMS 在熱失控前35 s 檢測出電池故障，基于EMD 與相關系數的方法在熱失控前61 s 準確檢測出故障，相較于BMS 自檢，將故障報警時間提前26 s。

圖5 基于EMD 與相關系數的方法與只使用相關系數、信息熵、高斯分布的結果對比

若不使用EMD 分解原始電壓數據，直接求取相關系數，結果如圖5(b)所示，其中時間序列的長度、窗口寬度保持一致，A 號單體與B 號單體相關系數的最小值為0.77，A 號單體與B 號單體具有強相關程度，難以判斷其電壓是否出現異常，因此基于EMD 與相關系數方法的準確性優于直接使用相關系數的方法。

為進一步體現本方法的優勢，將基于EMD 與相關系數的方法與可在線應用的高斯分布[9]、信息熵[4]進行對比，結果如圖5(c)和(d)所示。在圖5(c)中，基于高斯分布的方法在第893個采樣點檢測出故障，雖然其計算量較小，但檢測時間滯后于EMD 與相關系數的方法20 s。在圖5(d)中，基于信息熵的方法在第886～906 個采樣點(最后一個滑動窗口)都未能檢測出異常，因此基于EMD 與相關系數方法的準確性優于只使用信息熵的方法，檢測時間早于基于高斯分布的方法。

考慮到方法的適用性，若選取的B 號單體出現問題，則求得的所有相關系數均小于0.4，僅依靠閾值的方法會導致極高的誤報率，而人工觀察的方法難以將此方法推廣到大數據分析，同時故障早期檢測對時間要求較高，應減小算法計算時間實現故障快速檢測，因此采用計算量較小的有監督學習或無監督學習算法。有監督學習對訓練樣本數量要求較高且有效的故障數據難以獲取；而無監督學習不需要訓練集，采用無監督學習中的聚類算法并結合相關系數的閾值，確定基于“閾值+聚類”的故障單體智能識別方法。

本文選取無監督學習中的K-means 聚類算法，無需訓練集直接對異常單體進行篩選，將K設定為2，根據聚類結果可得到個數較少的一類和個數較多的一類，遵循故障單體為少數的原則，將個數較少且個數小于4 的一類歸為待定單體，若待定單體的相關系數均小于0.4 則判斷待定單體為故障單體；若個數較多的一類單體相關系數均小于0.4，則判定包含B 號單體在內的個數較少的待定單體為故障單體，進而實現故障單體自動辨識。

由于實際工況故障數據難以獲取，且熱失控多發于充電及靜置階段，為驗證方法的適用性和有效性，本文選取充電過程中熱失控案例二作為驗證，其電壓跌落趨勢與案例一相似。

案例二熱失控過程電池組單體電壓曲線如圖6 所示，單體充電截止電壓為4.2 V，在第1 619 個采樣點C 號單體電壓開始呈持續下降趨勢，在第1 629 個采樣點之后BMS 停止充電，此時模組最高單體電壓為4.191 V，未達到截止電壓4.2 V，模組最高溫度達99 ℃，第1 630 個采樣點模組最高溫度達113 ℃，推測已經發生熱失控。

圖6 案例二熱失控過程電池組單體電壓曲線

為實現故障早期檢測，本文選取第1(充電開始)～1 619 個采樣點電壓數據。針對充電電流不穩定導致的電壓曲線不平滑問題，采用EMD 對電壓序列進行分解得到穩態分量，采用滑動窗口的方法，窗口寬度設為30，計算每個窗口內D 號單體電壓穩態分量子序列與其余單體電壓穩態分量子序列之間的相關系數，結果如圖7 所示。由圖7 可知，C 號單體與D 號單體的相關系數最終下降到0.378，小于閾值0.4 且異常單體個數小于4，因此在第1 619 個采樣點本方法檢測出C 號單體電壓異常，需中止充電，此案例中BMS 未能提前檢測出電池故障，基于EMD 與相關系數的方法在熱失控前11 s 準確檢測出故障，說明此方法可以很好地實現鋰離子電池熱失控故障的早期檢測。

圖7 案例二窗口為30的D號單體電壓子序列與其余單體的相關系數

4 結論

本文從鋰離子電池熱失控案例入手，提出了一種基于EMD 與相關系數的電池熱失控故障早期檢測方法，主要工作如下：

(1)分析了案例一鋰離子電池熱失控過程，將熱失控過程中的電壓、溫度表現分為4 個階段，得到熱失控發生時電壓異常表現早于溫度異常表現的結論；

(2)對案例一第424～891 個采樣點的放電段電壓進行EMD 得到穩態分量，發現A 號單體穩態分量變化趨勢與原始電壓信號趨勢相同，采用滑動窗口計算窗口內B 號單體穩態分量與其余單體之間的相關系數，之后采用K-means 聚類算法實現故障單體自動辨識，最后選取熱失控案例二驗證方法的適用性。

本文將熱失控前的故障報警時間作為量化指標，在案例一中提出的基于EMD 與相關系數的電池故障早期檢測方法報警時間比BMS 報警提前26 s，實現熱失控前61 s 準確檢測出故障，且準確性優于只使用相關系數、信息熵的方法，檢測時間早于基于高斯分布的方法20 s，在避免誤報的前提下實現故障早期階段電壓異常檢測，在案例二中本文提出的方法在熱失控前11 s 準確檢測出故障，驗證了此方法的適用性，此外本方法計算量較小在BMS 中易實現，具有一定的應用價值。在后續的研究中，更多的熱失控電池數據將被用于驗證本文方法的適用性。