基于PBES-LS-SVM的鋰離子電池組SOC預測

李晟延，馬鴻雁,2,3，竇嘉銘，王 帥

(1.北京建筑大學 電氣與信息工程學院，北京 100044；2.建筑大數據智能處理方法研究北京市重點實驗室，北京 100044；3.智慧城市國家級虛擬仿真實驗教學中心，北京 100044)

鋰電池作為常用的環保儲能設備之一，對“3060”碳達峰、碳中和目標的達成起著重要支撐作用。鋰電池荷電狀態是反應電池性能的標準之一。鋰離子電池在使用過程中，準確預測電池組荷電狀態(state of charge，SOC)能夠及時預防電池過充、過放等違規操作對電池壽命造成損害。目前，SOC預測領域較為常用的方法有：卡爾曼濾波法[1]、傳統估計法[2]和數據驅動法[3]。

基于卡爾曼濾波法是SOC離線預測研究中較多的方法之一。王文亮等[4]采用最小二乘法實現電池模型參數的在線估算，結合擴展卡爾曼算法對SOC進行估算，預測精度得到了提高。但該方法需要依靠精確的電池等效電路模型，預測對象大多為單體電池，對于鋰離子電池組的SOC研究較少。傳統估計法分為開路電壓法與安時積分法，其中安時積分法[5]受溫度環境與充放電流影響較大，文獻[6]指出開路電壓法需要電池長時間處于靜止狀態，通過實驗得到端電壓與SOC之間的關系，該方法無法進行SOC的實時估計且溫度變化會對預測方式產生影響。劉春輝等[7]設計了基于SOC的DC/DC 變換器主動均衡電池管理系統，解決了動力電池組中各單體電池SOC值的不一致性問題，均衡效果較好。

數據驅動法可以略去電池內部的機理反應，將電池作為“黑箱模型”省去了參數辨識的過程，利用神經網絡建立起電池相關參數和荷電狀態之間的映射關系[8]。劉秋麗等[9]將粒子群算法優化BP 神經網絡模型應用在動力電池組荷電狀態的預測，驗證了粒子群算法優化模型的快速性與穩定性。孫小川[10]通過改進粒子群算法對BP 神經網絡進行優化，然后對網絡模型進行剪枝處理，對燃料電池組SOC進行預測，預測效果較好。但上述模型容易陷入局部最優，導致SOC預測精度較低。為解決這一問題，學者們提出將支持向量機[11-12]在小樣本和非線性預測問題上的優勢應用到鋰電池荷電狀態的預測中。

本文采用主成分分析對鋰電池組放電過程中的影響因素進行評估與篩選用于提高數據質量，利用新型元啟發式算法中的禿鷹搜索算法(bald eagle search，BES)對最小二乘支持向量機(least squares support vector machine，LS-SVM)中參數尋優環節進行優化，構成PBES-LS-SVM 網絡模型對鋰離子電池組的SOC進行研究，以獲得更加準確的電池組SOC預測模型。

1 預測模型

1.1 禿鷹搜索優化算法數學模型

禿鷹搜索優化算法是由馬來西亞學者Alsatter[13]在2020年提出的集群智能算法之一，自然界中，禿鷹的體型較大，這使得它們站在食物鏈的頂端[14]。禿鷹的狩獵階段分為三個階段：選擇空間、空間搜索獵物、俯沖[15]。禿鷹捕獵的三個階段數學模型如下：

階段1：選擇空間階段，盤旋的禿鷹，會基于鮭魚個體或種群的濃度來選擇空間。從原定位置朝選定的空間飛行。這一行為在數學上被定義為：

式中：α為控制位置變化的參數，取值范圍在[1.5,2]之間；r為(0,1)范圍內的隨機數；Dbest為當前禿鷹搜索確定的最佳搜索位置；Dmean為先前搜索結束后禿鷹的平均分布位置；Di為第i只禿鷹的位置。

階段2：空間搜索獵物階段，禿鷹通過在選定的螺旋空間內向不同方向移動來尋找搜索獵物。此外，確定最佳獵物和俯沖的最佳位置。獵取獵物和俯沖的最佳位置被確定。這種行為在數學上被定義為：

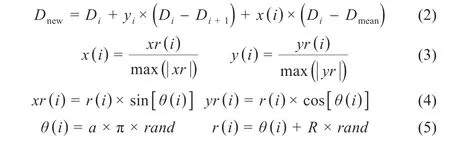
式中：Di+1為第i只禿鷹下一次更新位置；x(i)與y(i)為極坐標系下禿鷹的位置，取值范圍為(-1,1)；θ(i)為螺旋方程的極角；α為一個常數參數，取值范圍在[0,5]內；r(i)為螺旋方程中的極徑；R為另一個常數參數，取值范圍為[0.5,2]；rand為(0,1)之間隨機參數。

階段3：俯沖階段，禿鷹從搜索空間中的最優位置快速俯沖飛向目標獵物，禿鷹種群中其他個體也同時向最佳位置擺動俯沖攻擊獵物，定義為：

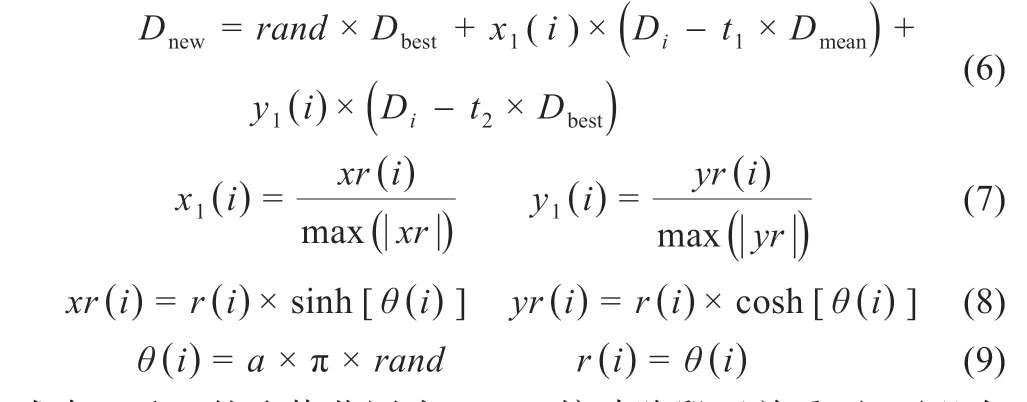
式中：t1和t2的取值范圍為[1,2]。俯沖階段至關重要，可以在設定的迭代次數中找到最優的解決方案。

1.2 最小二乘支持向量機

SVM 算法是一種以統計學理論為基礎的傳統機器學習方法，該方法可以在模型的復雜性與學習能力之間尋求最佳的折中，并獲得最好的推廣能力。而最小二乘支持向量機(LS-SVM)在傳統的SVM 上利用最小二乘線性系統作為損失函數，將SVM 中優化問題的不等式約束轉化為等式約束，以此對傳統SVM 進行優化。而BES 算法則是用來優化LSSVM 中的參數g與C的選擇，用于提高LS-SVM 中的性能與效率，更準確地對數據進行計算。

在鋰電池組SOC估算問題的研究背景下，非線性映射為ψ(x)，其主要目的是將其映射到一個高維空間中，以方便線性回歸運算的方法將低維的非線性轉換到高維空間中，并構造最優線性決策函數：

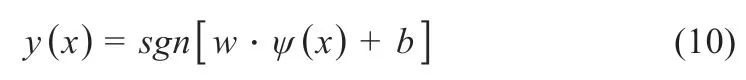
式中：w為權向量；b為常數。利用SRM 準則構造下面的最小化目標函數為[16]：

式中：y為調整參數；ei為松弛變量。通過核函數K(xi，xk)的引入可以得到LS-SVM 模型為[17]：

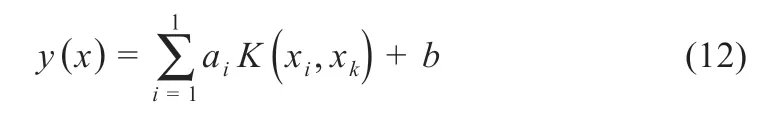
本文中，PBES-LS-SVM 網絡模型訓練集維度通過主成分分析法，將維度由原有的5 維降為3 維。高斯徑向基函數構造的支持向量機訓練參數相對較少，更容易確定參數，所以在核函數的選擇上采用高斯徑向基函數，即：

式中：z為高斯核寬度。

1.3 PBES-LS-SVM 預測模型

LS-SVM 中參數優化對于模型預測的準確性十分重要。因此本文選擇PCA 對鋰電池組放電過程中的影響因素進行評估與篩選用于提高數據質量，并利用元啟發式算法BES 優化參數g和C。其流程如圖1 所示。

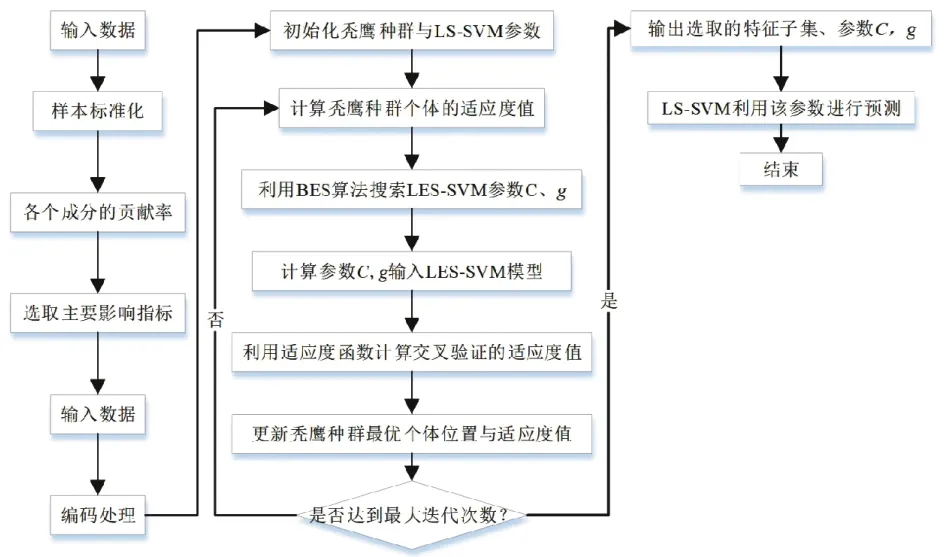
圖1 PBES-LS-SVM流程圖

具體步驟如下：

(1)選取儲能電站電池組的離線數據，提取數據編碼、電壓、電流、環境溫度等重要影響因素后，利用主成分分析對其進行研究。選取主要影響指標，再作為輸入數據參與模型的訓練。

(2)對數據進行編碼處理，初始化禿鷹種群LS-SVM 中的重要參數，懲罰系數C，核函數g等。

(3)計算禿鷹種群個體的位置，進行適應度值的計算，搜索、選取最優的空間。

(4)進入迭代循環，運用BES 算法更新參數。

(5)達到設定迭代次數后，判斷目標位置、目標值是否達到最佳，選取懲罰系數C，核函數g。

(6)LS-SVM 運用選取的參數，對鋰電池組荷電狀態進行預測。

2 數據采集與處理

2.1 數據采集

該研究數據為某儲能公司現場采集的鋰離子電池組的數據，電池組采用的為120 Ah 磷酸鐵鋰電芯，一個電池單元為2P16S，即2 個電芯并聯形成一個單體電池，再將16 個單體電池串聯構成一個電池單元。每個電池單元的容量為240 Ah，額定電壓為51.2 V。最終的電池組則是由14 個串聯的電池單元，總計224 個單體電池組成，其額定電壓為716.8 V。

對電池組數據進行整理清洗后，將異常數據舍棄。選取的因素包括數據編碼、電壓、電流、溫度、環境溫度以及電池組SOC的值。在獲得的數據中，電池溫度、環境溫度在一定時間段內變化范圍不大，樣本數據如表1 所示。

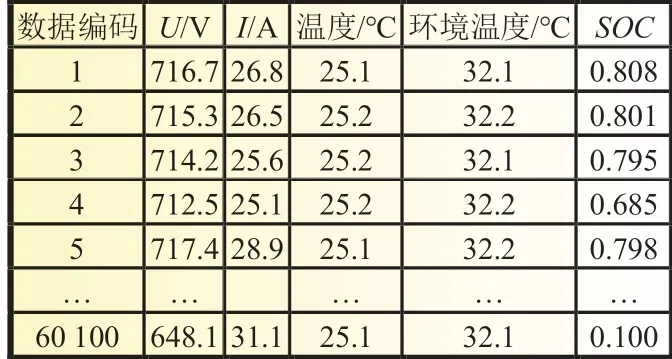
表1 電池組樣本數據

2.2 數據處理——主成分分析

PCA 是一種常用的對數據預處理的方法，原理是運用線性代數對原始數據進行降維與因素篩選，該方法可以將多個變量轉換為少數幾個不相關的綜合變量，能夠較全面地反應整個數據集。主成分分析的原理公式如式(14)：

式中：pR為1 個行向量，表示第R個基；aM為1 個列向量，表示第M個原始數據。

從n個原始變量中取出M個新變量來代替原始數據，其余的n-M變量對于原始信息的貢獻率較小可被代替。輸入變量越多，對SOC估算的精度越高，與此同時會造成整個模型的收斂性下降。

為減少后續預測模型的計算量，提高整個模型SOC估算的效率，通過PCA 針對表1 中電池組樣本數據變量進行綜合分析。其中，電壓、電流、數據編碼、溫度以及環境溫度為影響電池組SOC預測的指標。針對表1 進行主成分分析的結果如表2 所示。

表2 主成分分析結果

主成分提取原則通常按累計貢獻率或是主成分特征值提取主成分。根據表2 結果進行選取，成分x1、x2、x3的特征值均大于1，滿足特征值大于1 可作為主成分的條件，且所選變量累計方差貢獻率大部分大于80%，所以成分x1、x2、x3滿足作為主成分的條件，能夠反映原始數據中存在的信息。謝思宇等[18]利用主成分分析對NASA Ames 研究中心的電池數據進行分析，得出電池溫度對SOC估計的影響呈正相關。但當獲得的電池溫度與外部環境溫度變化范圍較小時，利用主成分分析得出的結論為：溫度與環境溫度對鋰電池組荷電狀態的影響不大。

因此，選取的成分為電壓、電流、數據編碼，以此作為輸入變量，在減小數據模型規模、維度的同時，消除變量間的相關性，盡可能地保留原始數據所含信息，增強禿鷹算法從現有數據中搜尋最優解的能力。

3 實驗結果分析

3.1 參數設定與誤差評價指標

禿鷹算法與遺傳算法都具有較強的全局搜索能力。關于遺傳算法的參數設定為進化代數為100，種群規模為20，代溝為0.9；禿鷹算法優化參數設置為進化代數為100，種群數目為20，優化個數為2。

通過主成分分析可以選取表1 中的電壓、電流、數據編碼作為輸入變量，電池組SOC作為輸出變量。針對上述選取的因素進行歸一化操作處理，該模型在預測得到數據之后，仍需要進行反歸一化處理。歸一化公式如下：

式中：yn為表1 中選定因素的原始數據；ymin和ymax為選定因素所有數據中的最小值和最大值；Yn為選定因素歸一化操作處理后的數據。

進行歸一化處理后，可以避免預測模型在預測時因訓練集與測試集量級差別過大，造成預測誤差較大的問題。禿鷹算法具備優秀的搜索能力，BES 中的禿鷹將歸一化處理后的數據作為模型的參數取值并將經過訓練得到的誤差作為目標函數，進行迭代尋優，找到最優個體的位置(即懲罰因子C與核函數g)作為最佳學習參數進行回代。LS-SVM 模型應用回代得到的最佳學習參數針對電池組SOC進行預測。

為分析各模型的可行性與有效性，本文主要采用以下4個誤差評價標準，即均方根誤差(root mean square error，RMSE)、平均絕對誤差(mean absolute error，MAE)、平均絕對百分比誤差(mean absolute percentage error，MAPE)、仿真運行時長(t)。公式如(16)～(18)：

式中：n為預測樣本個數；Yti表示第i時刻的實際SOC值；Yci表示第i時刻，模型預報得到的SOC預測值。各模型的仿真運行時長t，利用tic-toc 語句，進行自動計時。

3.2 結果與討論

為了驗證本文提出的PBES-LS-SVM 算法在鋰電池組SOC預測方面的有效性。選定鋰離子電池組完整的放電數據作為測試集，利用BES-SVM、PBES-LS-SVM 模型及SOC預測研究中常用的算法如GA-BP、GA-SVM 等模型進行獨立的SOC預測對比實驗。

圖2 為各模型的SOC預測結果與真實值的對比曲線。其中，圖2(a)為數據驅動以神經網絡為基礎的預測結果，從圖中可以看出，GA-BP 與GA-WNN 預測偏差過大。GA-BP 模型剛開始對SOC進行估計時，該模型的預測值與真實值差距不是很大，擬合度較好，但隨著估算樣本的增加，預測值有明顯的波動情況，個別預測樣本的結果逐漸偏離了SOC曲線，誤差隨之增大。GA-WNN 模型以小波函數代替原有復雜的網絡結構，與GA-BP 相比預測效果較好，但擬合效果仍然過差。

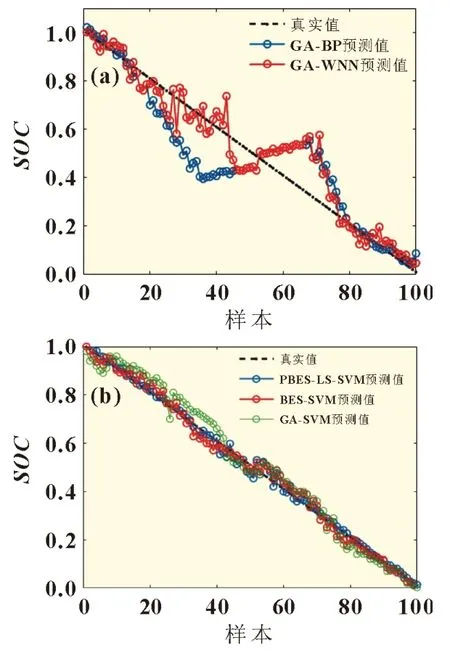
圖2 完整放電過程SOC預測結果

圖2(b)為數據驅動以支持向量機為基礎的預測結果。顯然，以支持向量機為基礎的三種預測模型，實際誤差優于上述兩種模型，預測結果更加逼近真實曲線，說明以支持向量機為基礎的改進模型更適合用于鋰電池組SOC的預測研究中。

從圖2(b)中可以看出，PBES-LS-SVM 的SOC預測模型與真實值更接近，表現出良好的收斂效果和預測效果。絕對誤差是預測值與真實值存在的實際偏差，圖3 為SOC預測模型的絕對誤差對比。

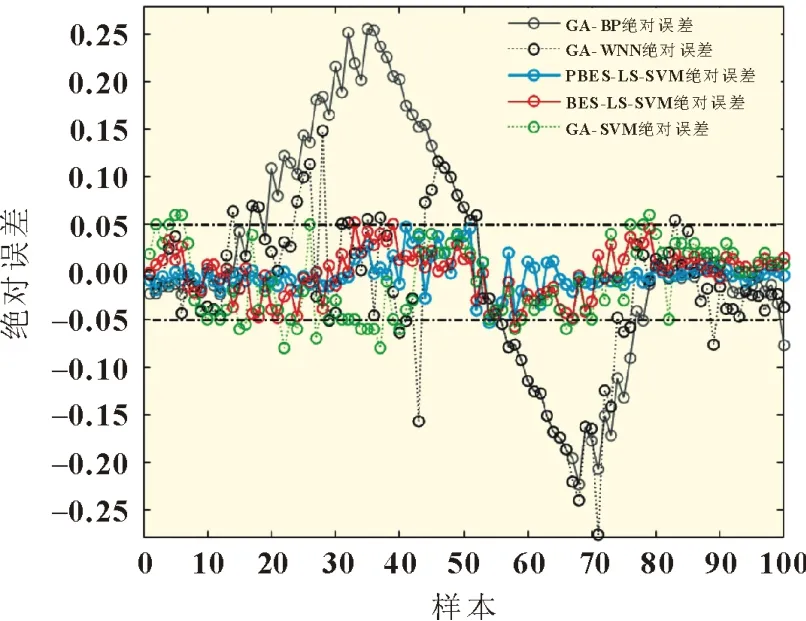
圖3 SOC絕對誤差對比

從圖3 可以看出，BES-SVM 模型的絕對誤差處于[-0.060,0.060]區間范圍，GA-SVM 的絕對誤差處于[-0.070,0.070]區間范圍，GA-WNN 與GA-BP 模型預測出現了較大的誤差，擬合度較差。而PBES-LS-SVM 模型的絕對誤差均處于[-0.050,0.050]區間范圍，最大絕對誤差僅為0.047。這證明了PBESLS-SVM 模型預測鋰電池組放電狀態SOC的可行性。

此外，表3 為五種模型的實驗指標數值對比。結果顯示，PBES-LS-SVM 算法在RMSE、MAE、MAPE和運行時間t四個評價標準下均優于其他算法預測模型，預測性能優越。

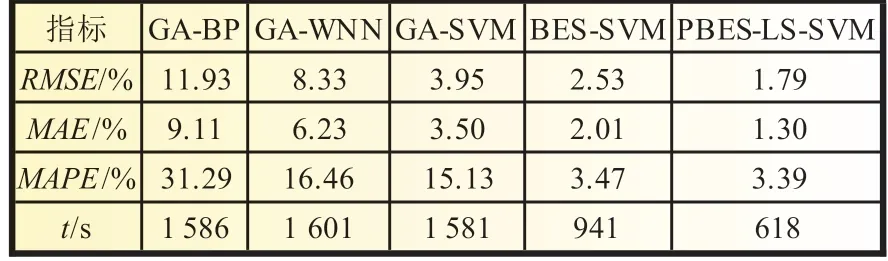
表3 模型誤差結果對比

在全放電過程的驗證基礎上，隨機采取部分數據集共10 100 組，驗證PBES-LS-SVM 模型在局部放電過程中的預估性能。圖4 為各模型預測局部放電過程的結果。

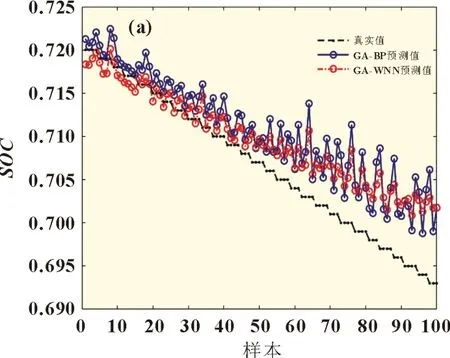
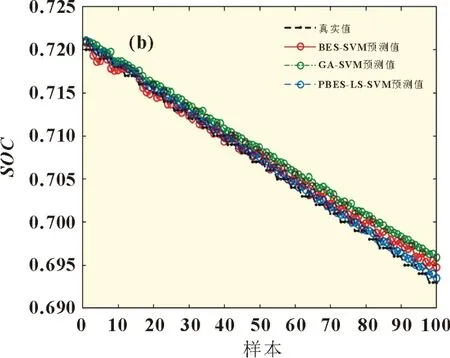
圖4 局部放電過程SOC預測值對比

其中，圖4(a)為數據驅動GA-BP 和GA-WNN 模型的預測結果，由曲線可以看出，預測值大幅度偏離實際值，擬合效果較差。此外，在仿真過程中發現，以神經網絡為基礎的數據驅動模型隨著仿真次數增加，GA-BP 和GA-WNN 模型的仿真結果變化不大，模型陷入了局部最優解。由圖4(b)可知，將PBES-LS-SVM 與BES-SVM 進行對比，利用最小二乘線性系統作為損失函數優化支持向量機，可以提升預測的擬合度。對比GA-SVM 與BES-SVM 模型的預測結果，可以發現：利用禿鷹算法優化支持向量機的預測值與真實值的波動幅度更小。

圖5 為各模型100 組的絕對百分比誤差。由圖5 可知，以SVM 模型為基礎的絕對百分比誤差均在[-5×10-3，5×10-3]內。其中，PBES-LS-SVM 模型的最大絕對百分比誤差為1.6×10-3。仿真表明，被主成分分析優化數據集后的BES-LS-SVM 模型預測結果與實際值擬合程度較好。以鋰離子電池局部放電過程數據為基礎的模型性能對比，如表4 所示。

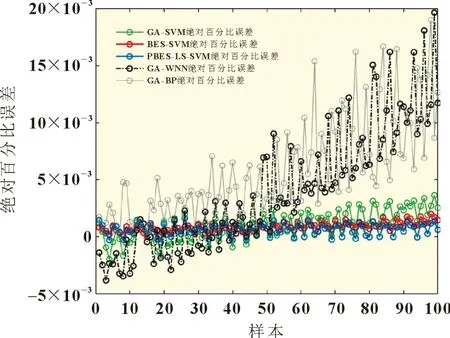
圖5 絕對百分比誤差曲線圖

表4 SOC 預測誤差對比

表4 記錄了PBES-LS-SVM、BES-SVM 等預測模型在面對隨機部分數據時的預測誤差對比。由圖5 和表4 可知，PBES-LS-SVM 模型的RMSE和MAE值最小，分別達到0.81%和0.41%，說明該模型仍保持良好的擬合能力，預測性能較好。

4 結語

為實現準確、快速預測鋰離子電池組SOC，避免利用神經網絡易陷入局部最優的問題，本文提出一種基于主成分分析和禿鷹算法優化LS-SVM 模型的鋰離子電池組荷電狀態預測模型。主要結論如下：

(1)利用主成分分析處理數據選取主成分系數較高的因素作為BES-LS-SVM 模型的訓練集，可以減小變量間相互影響，提升數據質量。

(2)采用禿鷹算法優化LS-SVM 中的懲罰系數C和核函數g，增強了模型的全局搜索能力和計算能力，提升了SVM 模型的擬合能力。

(3)仿真結果顯示，以支持向量機為基礎的預測模型更適用于鋰離子電池組荷電狀態的預測。本文提出的PBES-LSSVM 模型誤差低，具有良好的追蹤性、快速性和泛化性，能夠滿足SOC精確估算的工程要求。