基于仿真模型的垂直熱場溫度控制技術研究

李瑫，楊勇，孫龍，陳李松，黃志海

中國電子科技集團公司第四十八研究所，湖南 長沙 410111

0 引言

某垂直工藝設備加熱系統比較復雜，包括爐體、外管、內管、隔熱盤以及上端冷凝等部分，其垂直傳熱模型邊界條件非常復雜，熱負載很不均勻，管內溫度分布情況尚不清楚，溫度分布的可調節因素及其影響規律也不明確。因此如何實現垂直熱場的溫度精密控制，是該設備研制的關鍵難點技術之一。本文采用仿真研究的方法，分析反應管內溫度分布情況及可調節因素對內部溫度場的影響規律，通過對大量仿真數據進行學習，在目標溫度附近建立管內恒溫區溫度分布與爐體溫度的線性化模型，并進行測試驗證。

1 傳熱數學模型

此加熱系統中，能量由外界通過電流、電壓形式輸入，通過電熱絲發熱后形成熱源。加熱絲與金屬外管之間主要通過熱輻射和氣體對流方式傳熱，金屬外管壁上主要通過熱傳導方式傳熱，在上部通過冷卻水帶走熱量，金屬管內部則主要通過熱輻射和對流方式傳熱，最終在石英管內形成溫度場。下面對三種傳熱形式的數學模型進行分析。

1.1 輻射傳熱

輻射傳熱是指物體之間相互輻射和吸收的總效果，主要考慮物體表面因溫度而產生的輻射，包括表面對表面的輻射傳熱。單位時間內離開物體表面單位面積的總輻射能稱為有效輻射，它包括自身輻射和投入輻射中被表面反射的部分。對于特定表面，其能量收支差額應等效于有效輻射與投入輻射之差。因此，實際物體表面有效輻射J與表面凈輻射換熱量q之間的關系如下[1]：

1.2 熱傳導

對于固體或液體中的熱傳導，必須滿足由能量守恒定律和傅里葉定律所建立的導熱微分方程，其在笛卡爾坐標系中的一般形式如下[2]：

1.3 對流傳熱

流體流過固體表面時，流體與固體間的熱量交換稱為對流傳熱。為簡化數學模型，假定流體為不可壓縮的牛頓流體，流體物性為常數、無內熱源，且忽略粘性耗散產生的耗散熱，可以用Navier-Stokes方程來描述上述流體的對流傳熱。但由于數學上的困難，只有極少數情況才能獲得上述方程的分析解，因此需運用數量級分析的方法對方程作實質性的簡化，并假定流動為二維、穩態邊界層型的對流，其控制方程式[3]為：

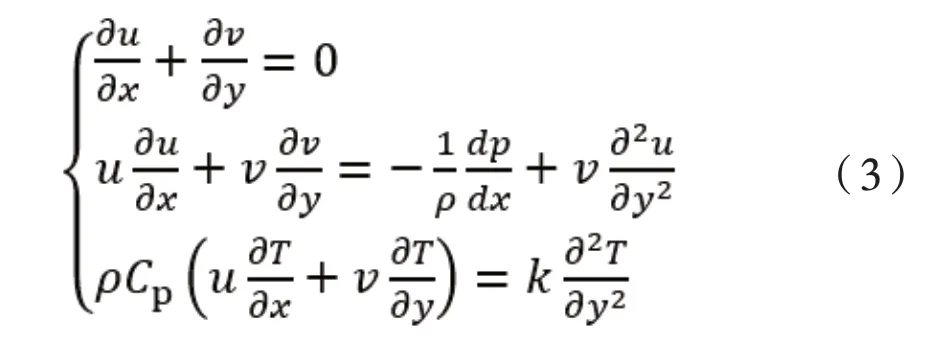
式（3）中，ρ為物體的密度，Cp為物體在常壓下的比熱容，k為材料的導熱系數，[u，v]為流體的速度場，p為單位體積內流體的動量。

2 溫度仿真分析

本研究采用Comsol軟件進行建模仿真。Comsol是基于通用的高級數值方法和模擬物理場問題的模擬平臺，是一款真正的任意多物理場直接耦合分析軟件，具有方便、易用、高效、專業模擬計算平臺的特點，廣泛應用于各個領域的科學研究以及工程計算。

2.1 仿真模型建立

仿真的幾何模型采用柱面坐標系，結構包括爐體、熱源、外管、內管、隔熱盤等。爐體由6段加熱絲上下對稱繞制，并由6個測溫熱偶分別檢測溫度；外管采用高強度特種鋼材，滿足內部11個大氣壓的強度要求，其下部置于爐體內加熱，上部外壁采用循環水冷卻；內管自由放置于外管內，用于盛放反應液，其內外連通，因此管壁不承受高壓；隔熱盤采用石墨材質，多片層疊，依靠自身重力放置于內管內壁的凸臺處，用于阻隔管內氣體的上下對流傳熱。為每個結構添加對應的材料，并完善材料的密度、傳熱系數等相關參數。模型中添加固體傳熱、流體傳熱以及表面輻射傳熱三種物理場進行耦合計算，研究穩態和瞬態下石英內管內部橫截面及軸向的溫度分布。為與實際控溫情況保持一致，模型中6段加熱絲采用表面溫度熱源設定（其中加熱絲4和5同屬于溫區4，設定溫度相同），熱源溫度從室溫按斜率增加到設定值后保持穩定。模型設計輸入變量包括5個溫區的設定溫度、管內壓力、冷卻水流量，研究這些因素對管內溫度場的影響。

2.2 仿真及分析

2.2.1 熱場的溫度分布

設定爐體各溫區按12℃/min的速率升溫至500℃，對管內溫度分布進行瞬態研究，設置時間步為（0，900，10）min，即計算從0時刻間隔10min到900min的溫度分布，并繪制管內從底部沿中軸線往上的溫度分布，結果如圖1所示。

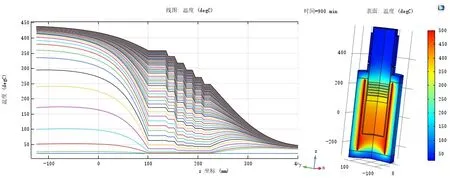
圖1 管內熱場溫度分布仿真結果

從圖1中可以看出，管內軸線上，整體從上到下溫度升高；底部隔熱盤以下區域與上部冷卻區域的溫度變化比較平緩，中間段溫度變化梯度很大；隔熱盤有效降低了底部區域的溫度下降梯度。

2.2.2 設定溫度對熱場的影響

由于金屬外管的均熱效應，各溫區溫度變化對管內溫度的耦合影響顯著增強，使得管內溫度的調節更加復雜。通過在研究中添加參數化掃描，分別對各個溫區單獨研究計算設定溫度為（500，20，600）℃范圍內的管內溫度分布并繪制曲線，可以得到各溫區對管內溫度分布的影響情況。

根據仿真結果可知：溫區4設定溫度的變化對恒溫區影響最大，溫區3設定溫度的變化對恒溫區上段有較大影響，溫區2設定溫度的變化對恒溫區上端點影響較大，溫區1和溫區5設定溫度的變化對恒溫區上端點、下端點有輕微影響。由此可總結出恒溫區的調試設定方法：溫區1、2盡量設置高，調節溫區4使恒溫區到目標溫度附近，溫區3、4決定恒溫區最高溫度（3高4低）；溫區5調節下端點。按照上述方法，通過多次仿真，在5個溫區設定溫度為（610，610，545，475，520）℃時，獲得了較好的恒溫區溫度分布，如圖2所示。圖中，底部往上前100mm即[-120，-20]mm范圍內最大溫度偏差為0.68℃，150mm即[-120，30]范圍內最大溫度偏差為5.76℃。

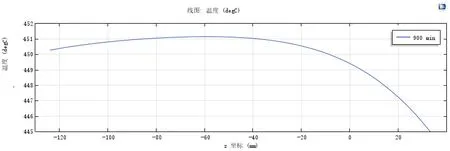
圖2 仿真得到的恒溫區溫度分布圖

2.2.3 其他因素的影響

（1）管內壓力的影響。管內壓力對穩態溫度分布無明顯影響；但壓力升高可加快管內氣體內部傳熱，使管內上、下部溫度分布更均勻。因此瞬態仿真研究中，在加熱前期的同一時刻，內管底部的溫度隨著壓力的升高而降低，而上部則隨著壓力的升高而升高；當溫度分布趨于穩定后，壓力的變化對溫度分布幾乎無影響。

（2）冷卻效果的影響。冷卻水溫度及流量均影響外管上部的散熱能力，進而影響內部溫度分布。通過仿真發現，隨著冷卻水出口溫度的升高，管內溫度曲線整體上升，但上升的幅度非常微小，說明冷卻水溫及流量對管內溫度分布影響非常微弱，對于溫度的調整控制可以忽略。

3 溫度控制設計及驗證

3.1 溫度控制方法設計

上文通過仿真在設定溫度（610，610，545，475，520）時獲得了較好的恒溫區溫度分布，因此本文嘗試在此設定溫度附近建立設定溫度與恒溫區溫度分布的線性化關系。令：

式中，T為恒溫區內0～150mm每隔10mm的溫度值，Ts第一項為1，后五項為溫區1～5的設定溫度，W表示各溫區設定值變化對T的影響權重，是16×6的矩陣。

在Comsol仿真模型的研究中，利用參數化掃描分別對每個溫區的設定溫度按照表1的范圍和間隔（[a，b，c]表示從a按c的間隔增加到b）進行仿真計算，將仿真數據導出整理，對于恒溫區的每個位置點，可得到11組溫度與各溫區設定溫度的對應數據。對于式（5）的每一行，展開后可變為：

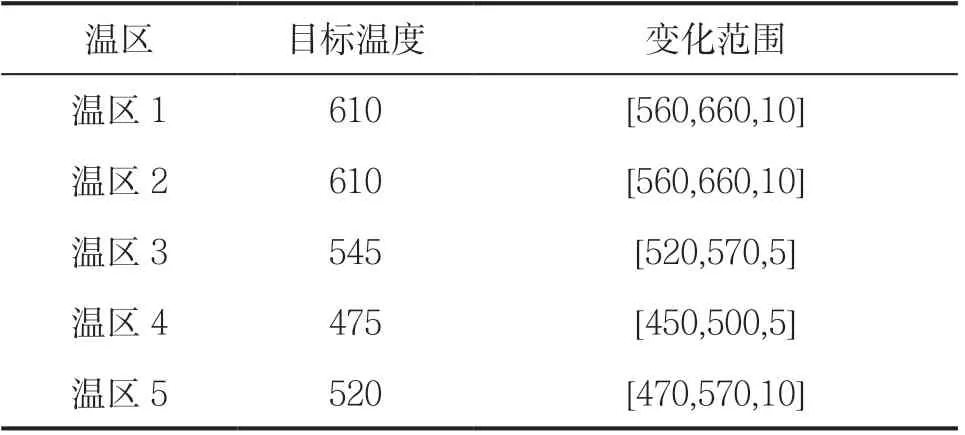
表1 各溫區參數化掃描溫度及范圍

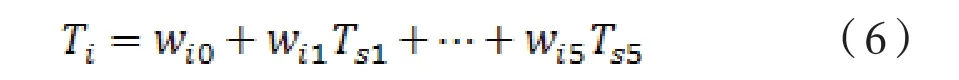
在已知和的情況下求系數，這是一個多元線性回歸問題，可根據最小二乘法原理，利用正規方程組[4]計算得到，進而組合得到權重矩陣W。

對式（4）兩邊同時左乘W的轉置矩陣WT，得：

3.2 測試結果

按固定斜率增加各溫區的加熱溫度至設定值后穩定一段時間，再對內管軸線上的溫度進行測試，測試條件見表2，測試結果曲線見圖3。

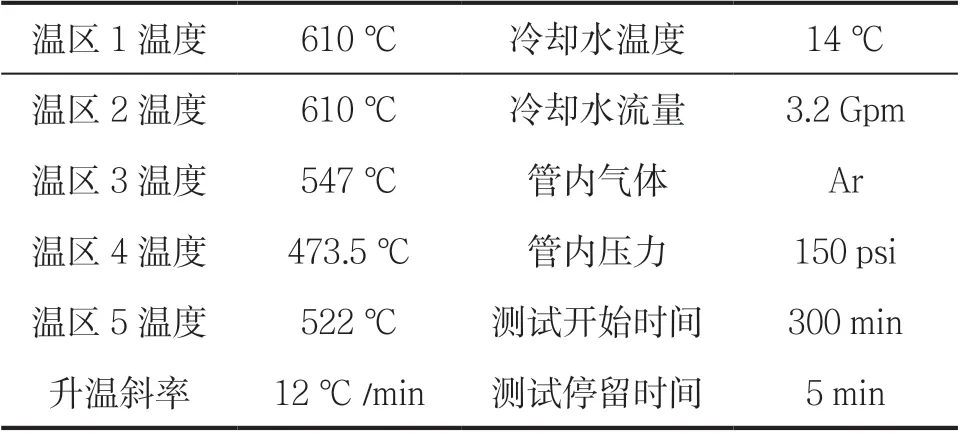
表2 恒溫區測試參數

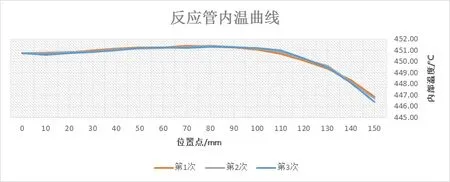
圖3 實際設備恒溫區測試結果

由圖3可見，恒溫區前100mm溫度變化平穩，最大溫差為0.72℃；在100mm之上溫度加速下降，150mm范圍內最大溫度偏差約5℃。恒溫區的整體溫度趨勢與仿真結果（圖2）保持一致，由此說明仿真結果與實際情況吻合較好。

設定恒溫區內期望溫度升高到460℃，然后快速下降到420℃，再按照0.15℃/min的降溫速率下降到408℃。按照上文給出的數學模型計算并設定爐體加熱溫度，利用管內軸線上的內部測溫點（約位于底部往上100mm處）測量恒溫區溫度，其期望曲線（深灰色）及實際曲線（洋紅色）如圖4所示。

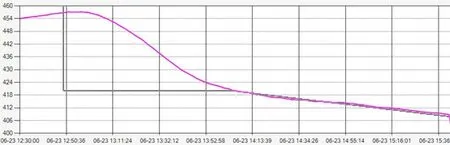
圖4 恒溫區內溫度跟隨曲線

從圖4中可以看出，實際恒溫區內部溫度曲線在斜率降溫段跟蹤效果良好，通過查看溫度數據發現實際溫度與期望溫度的最大偏差為0.43℃，斜率溫度跟蹤精度滿足實際工藝使用的要求。

4 結語

通過仿真研究可知，該垂直熱場管內溫度分布整體底部高上部低，兩端溫度變化相對平緩，中間段溫度梯度很大；各溫區的爐體溫度是管內溫度分布的主要影響因素，其中溫區3和4對恒溫區影響最大，而管內壓力以及冷凝效果對溫度分布影響很小；該垂直熱場恒溫區的調試方法為：溫區1、2盡量設置高，調節溫區4使恒溫區到目標溫度附近，溫區3、4決定恒溫區最高溫度（溫區3盡量高溫區4盡量低），利用溫區5調節下端點的溫度；在恒溫區附近通過對仿真數據進行學習，幾乎一定可以得到的線性化控制模型；實測恒溫區曲線與仿真結果一致，說明仿真模型與實際情況吻合良好；利用線性化模型控制恒溫區溫度的斜率跟蹤精度≤0.43℃，滿足工藝使用要求，說明該方法準確有效。