犁刀式混合機飛刀軸結構設計及臨界轉速計算*
鄒俊偉
(湖南探索機械科技有限公司,湖南 株洲 412000)
0 引 言
犁刀式混合機作為物料顆粒混合工序工業生產中的關鍵設備,在飼料工業、食品、制藥、化工、新能源鋰電材料、工程塑料等領域具有非常廣泛的應用前景[1-4]。
根據犁刀式混合機工作原理,飛刀軸在驅動電機帶動下高速旋轉(3 000 r/min 左右),可以起到剪碎物料顆粒中的塊狀物料并強烈擴散物料,加強物料顆粒的混合等作用,其一般安裝在腔體上并與腔體水平面成一定的角度[5]。 飛刀軸的可靠性直接關系到混合機的可靠性及混合效率,而飛刀軸的可靠性取決于飛刀軸的結構設計及臨界轉速確定(橫向振動問題),所以解決上述兩個問題是保證飛刀軸可靠性的前提和關鍵。
針對飛刀軸的結構設計及臨界轉速計算問題,首先建立飛刀軸受力分析模型,通過飛刀軸受力分析,利用極限計算法確定飛刀軸的最小軸徑,再通過有限元法計算出飛刀軸的臨界轉速并驗證計算結果的準確性,最后根據有限元計算結果反推出飛刀軸軸承支撐距離與軸總長之比μ≈0.3 時的支座型式系數λ1,計算方法及結果可為犁刀式混合機飛刀軸的設計提供參考和依據。
1 飛刀軸結構設計
飛刀軸工作狀況為高速低載,主要承受剪碎塊狀物料顆粒時塊狀物料顆粒施加的阻反力矩TF及物料顆粒施加的摩擦阻反力矩Tf,摩擦力矩Tf由飛刀端面所受摩擦力力矩Tf1和側面所受摩擦力矩Tf2合成:

上述力的作用使飛刀軸承受扭矩作用,得出飛刀軸受力分析圖見圖1。

圖1 飛刀軸受力分析
根據圖1,飛刀所受物料顆粒的重力由兩部分組成,一部分為飛刀端面方向物料顆粒重力m1g,另一部分僅為飛刀側面方向物料顆粒重力m2g。 設飛刀掃略區域為l(即最大飛刀直徑在水平面投影長度),最低層飛刀至腔體內壁高度為h=1.2 m,則飛刀掃略區域的物料顆粒質量為M1,計算公式:

易知:

按極限法計算取:

鑒于物料顆粒混合時其運動軌跡的復雜性,將飛刀所受摩擦力按保守簡化計算,即將離散的物料顆粒視為連續的整體。
飛刀端面上所受物料顆粒正壓力:

則,飛刀端面所受最大摩擦力力矩:

式中:rmax1為最大摩擦半徑,取0.09 m;f1為物料顆粒與飛刀摩擦系數,取0.6;θ為飛刀軸安裝角度,取20°;g 為重力加速度,取10 m/s2。
創立于1945年的德國雄克公司 (SCHUNK GmbH & Co. KG) 是全球知名的抓取系統與夾持技術供應商。共有超過2 800名員工、9個工廠、位于50多個國家的33家子公司和代理合作伙伴,共同維護并拓展全球市場。雄克可提供11 000種標準部件,包括 2 550款標準機械手;由4 000多種自動化模塊組成的完整抓取系統。雄克服務的目標行業包括機械工程、機器人、自動化裝配及搬運以及所有知名的汽車生產商及零部件供應商。
飛刀側面物料顆粒對腔體壁的正壓力:

則,飛刀側面所受摩擦力力矩為:

式中:rmax2為最大摩擦力臂,取0.09 m;f2為物料顆粒與腔體壁摩擦系數,取0.6;θ為飛刀軸安裝角度,取20°。
聯立式(1)、(6)、(8)并代入數據得:
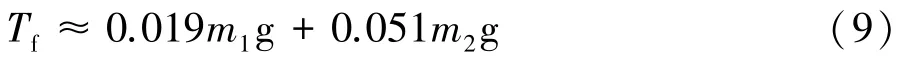
聯立式(4)、(9)進一步可得:

聯立式(2)、(10)得:

設飛刀剪碎塊狀物料顆粒時剪碎力為F,則:

式中:h為塊狀物料顆粒高度,取10 mm;b為犁刀與塊狀物料顆粒接觸寬度,取4 mm;σ為塊狀物料顆粒剪切強度,取1.3 MPa;f為物料顆粒與腔體內壁摩擦系數,取0.6。
數據代入式(12)得:

式中:rmax為最大飛刀半徑,取0.09 m。
根據式(11)、(13)計算飛刀承受的阻反力矩:

按扭轉強度計算飛刀軸最小軸徑[6-7]:

式中:T為軸所傳遞的扭矩,24 000 N·mm;τp為許用扭轉切應力,取30 MPa。
代入得:

2 飛刀軸臨界轉速計算
2.1 理論計算飛刀軸一階臨界轉速
為避免飛刀軸工作時發生彎曲共振(橫向振動),飛刀軸作為剛性軸,其最高轉速應低于一階臨界轉速,即飛刀軸最高轉速應滿足如下條件[8]:

式中:ncr1為飛刀軸一階臨界轉速,r/min。
因飛刀軸為雙絞支支撐方式并計軸自重(飛刀軸、飛刀材質為SUS304 不銹鋼),用鄧柯萊(Dunkerley)簡化公式求其一階臨界轉速[7]:

式中:λ1為一階臨界轉速時支座型式系數;W0為軸所受重力,11.48 N;L為軸全長,285 mm;l為支撐間距離,84.7 mm;Gj為外伸端第j個圓盤(飛刀)所受重力,N;cj為外伸端第j個圓盤(飛刀)至支撐間的距離,mm。 參數見表1;dv為軸的當量直徑,mm。
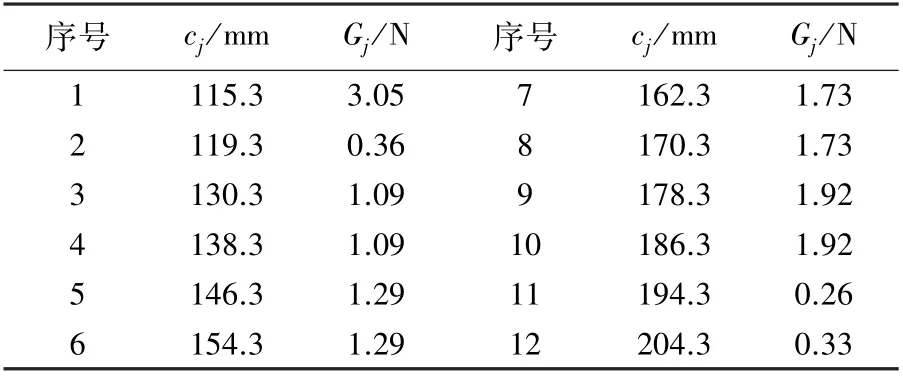
表1 等效圓盤(飛刀)支撐參數
飛刀軸的當量直徑按下式計算[7]:

式中:di為第i段軸直徑,mm;Δli為第i段軸長度,mm。 參數見表2;ξ為經驗修正系數,取1.094。

表2 飛刀軸軸段參數 /mm
因飛刀軸支撐間距離μL與軸總長L之比μ=0.3,見圖2[7],通過查閱機械設計手冊或相關文獻,無對應的支座型式系數λ1。 為確定λ1取值,利用有限元計算軟件計算出飛刀軸一階臨界轉速,再取可選的支座型式系數λ1,結合理論計算驗證有限元計算的準確性,最后根據有限元計算出的飛刀軸一階臨界轉速結果反推出μ=0.3 時的一階臨界轉速對應的支座型式系數λ1。

圖2 軸支撐距離與軸總長度之比
2.2 有限元法計算飛刀軸一階臨界轉速
對飛刀軸進行頻率分析,在有限元計算軟件中導入飛刀軸實際三維模型并劃分網格,飛刀軸有限元計算模型見圖3。

圖3 飛刀軸有限元模型
飛刀軸的約束為雙支點軸承約束。 因飛刀軸承受載荷類型為力矩,而力矩載荷對結構固有頻率影響甚微,在此忽略,所以飛刀軸頻率分析時不施加力矩載荷。 頻率分析結果見圖4。

圖4 飛刀軸頻率有限元計算
由圖4 可知,飛刀軸一階固有頻率為180.54 Hz,通過進一步計算可得到飛刀軸的一階臨界轉速約為10 832 r/min。
3 飛刀軸臨界轉速理論與有限元法計算比較
為反推出μ=0.3 時飛刀軸一階臨界轉速理論計算時對應的支座型式系數λ1,并驗證有限元計算的準確性,分別取λ1=0.5、0.55、0.6,其余參數保持不變,再分別根據式(18)、(19)對比理論和有限元法計算結果。 計算結果見表3 所列。

表3 不同λ1 時一階臨界轉速計算結果及誤差
根據表3,理論計算與有限元法計算飛刀軸一階臨界轉速最大誤差為4%,進一步可以確認理論計算及有限元法計算飛刀軸一階臨界轉速的準確性,從而可根據圖4 計算結果及式(18)、(19)反推出μ=0.3時飛刀軸一階臨界轉速理論計算時對應的支座型式系數λ1。 按最大誤差4%計算,取比有限法計算結果小的值,得λ1=4.49。
聯立式(17) ~(19)得出飛刀軸一階臨界轉速ncr1min為:

取飛刀軸最小一階臨界轉速ncr1min為飛刀軸一階臨界轉速。 進一步,根據式(17),可得飛刀軸轉速ωmax最大值為:

4 結 語
針對飛刀軸的結構設計及臨界轉速計算問題,首
先建立飛刀軸受力分析模型,通過飛刀軸受力分析,利用極限計算法得到飛刀軸最小軸徑取16 mm 可滿足強度要求,再通過有限元法計算得到飛刀軸的臨界轉速為7 798 r/min,并結合理論計算方法驗證了計算結果的準確性,最后根據有限元計算結果反推出飛刀軸軸承支撐距離與軸總長之比μ≈0.3 時的支座型式系數λ1=4.49。 計算方法及結果可為犁刀式混合機飛刀軸的設計提供參考和依據。

