面向高維特征缺失數據的K最近鄰插補子空間聚類算法

喬永堅，劉曉琳，白亮*

面向高維特征缺失數據的K最近鄰插補子空間聚類算法

喬永堅1，劉曉琳1，2，白亮1，2*

（1.山西大學 計算機與信息技術學院，太原 030006； 2.計算智能與中文信息處理教育部重點實驗室（山西大學），太原 030006）（?通信作者電子郵箱bailiang@sxu.edu.cn）

針對高維特征缺失數據在聚類過程中面臨的因數據高維引發的維度災難問題和數據特征缺失導致的樣本間有效距離計算失效問題，提出一種面向高維特征缺失數據的K最近鄰（KNN）插補子空間聚類算法KISC。首先，利用高維特征缺失數據的子空間下的近鄰關系對原始空間下的特征缺失數據進行KNN插補；然后，利用多次迭代矩陣分解和KNN插補獲得數據最終可靠的子空間結構，并在該子空間結構進行聚類分析。在6個圖像數據集原始空間的聚類結果表明，相較于經過插補后直接進行聚類的對比算法，KISC算法聚類效果更好，說明子空間結構能夠更加容易且有效地識別數據的潛在聚類結構；在6個高維數據集子空間下的聚類結果顯示，KISC算法在各個數據集的聚類性能均優于對比算法，且在大多數據集上取得了最優的聚類精確度（ACC）和標準互信息（NMI）。KISC算法能夠更加有效地處理高維特征缺失數據，提高算法的聚類性能。

高維數據；特征缺失；插補算法；子空間結構；聚類

0 引言

隨著科技的不斷進步，數據采集設備性能逐漸增強，人們所獲取數據的維數越來越高。現實生活中存在很多高維數據，如圖像數據、用戶評分數據、貿易交易數據、Web文檔數據、基因表達數據等。人們可以從這些高維數據中獲得更豐富的信息，使各個領域的生產生活更加便利，但是這些高維數據通常具有冗余信息量大、信息分布不均的特點［1］，且數據維度過高會造成維度災難問題［2］。在高維空間下，數據點之間的距離基本相等，使樣本間相似性度量方法失效；同時，高維數據也容易受到噪聲和數據缺失問題的影響。因此，高維數據給數據挖掘任務帶來了巨大的挑戰。

數據在產生和收集過程中，由于某些原因，會出現數據特征缺失的情況，如樣本的個別屬性值缺失，而高維數據更容易受到數據缺失問題的影響形成高維特征缺失數據。高維特征缺失數據中同樣蘊含著豐富的信息，需要人們進行挖掘。聚類分析技術是數據挖掘中的一個重要分支［3］，目的是將一組給定的數據依據它們的相似性劃分為不同的簇，該劃分使得相同簇中的樣本盡量相似，不同簇中的樣本盡量不同。常見的高維數據聚類算法包括核K?Means聚類［4］、譜聚類［5］以及子空間聚類［6］等。這些聚類算法已被廣泛應用到各大領域中，如生物信息分析［7］、醫學圖像分析［8］、社交網絡［9］、圖像分割［10］以及推薦系統［11］等。研究人員可以使用聚類分析技術來挖掘高維特征缺失數據中的隱藏信息，但是這個過程不僅需要解決數據高維引發的維度災難問題，還要解決數據特征缺失導致的樣本間有效距離計算失效的問題，加大了聚類分析的難度。

高維特征缺失數據由于信息不完整，無法使用常見的高維數據聚類算法進行分析。現有的解決方案需要先將高維特征缺失數據插補完整，再對完整的數據進行聚類分析。插補高維特征缺失數據時，受到維度災難和數據特征缺失導致的樣本間有效距離計算失效問題的影響，得到的插補值會扭曲原始數據的潛在結構，使得到的完整數據用于聚類分析時，表現不佳。將高維特征缺失數據補全后，對補全后的完整數據進行聚類分析。如果使用一般的聚類算法，由于沒有解決維度災難問題，在計算樣本間相似性時，基于距離的相似性度量方法受到維度災難的影響變得不可靠，必然會影響最終的聚類結果，所以需要對插補后的完整高維數據進行降維處理。采用矩陣分解法［12］學習高維數據的子空間結構可以解決維度災難問題，但是得到的子空間結構會受插補算法的影響，因此選擇一種合適的插補算法尤為重要。

因此，本文提出一種面向高維特征缺失數據的K最近鄰（K?Nearest Neighbor， KNN）插補子空間聚類（KNN Imputation Subspace Clustering， KISC）算法。該算法主要是將矩陣分解和KNN插補進行有機融合，利用數據的子空間下的近鄰關系去插補原數據的缺失特征，通過迭代優化數據的子空間表示和原數據插補值，使子空間結構更加穩定可靠，最終利用穩定的子空間結構去識別數據的潛在聚類結構。最后，在6個高維數據集上對該算法和已有算法進行了實驗分析，結果表明本文提出的KNN插補子空間聚類算法非常適合高維特征缺失數據的聚類分析。

1 相關工作

現實生活中的大量數據都存在一定程度的缺失，如何對缺失數據進行聚類引起學者們的廣泛討論。目前對高維特征缺失數據聚類需要先進行插補，然后在完整的高維數據集上進行聚類。

已有插補算法可以分為兩大類：基于統計學的插補算法和基于機器學習的插補算法。

基于統計學的插補算法運用統計學領域的算法對缺失數據進行處理，如均值插補、冷平臺插補、熱平臺插補、回歸插補和模型插補等。Kalton等［13］在熱平臺插補法的基礎上提出樹枝分類的距離函數匹配法，使回歸插補和熱平臺插補存在的相關性和回歸系數偏差大的問題得到解決。Dempster等［14］提出的期望值最大化（Expectation Maximization， EM）算法在求解缺失值時可以加入求解目標的額外約束。EM算法的不足在于：如果數據集中缺失值的比率過高，EM算法會因為緩慢的收斂和繁瑣的計算過程導致估計值與真實值的偏差過大。Little等［15］總結并克服了EM算法的不足，提出了多重插補（Multiple Imputation，MI）法。金勇進［16］介紹了演繹估計、均值插補、隨機插補、回歸插補和多重插補算法的理論知識。熊巍等［17］結合修正的EM算法，提出了基于R型聚類的Lasso?分位回歸插補法，解決了高維成分數據的近似零值問題。Lux等［18］為任意維度的線性插值提供了一種創新的誤差界定，將某些插值技術的性能與常用的回歸技術進行了對比，并通過實驗結果驗證了插值對于中等高維稀疏問題的可行性。

基于機器學習的插補算法借鑒機器學習的各種算法對缺失數據進行處理。武森等［19］針對分類變量不完備數據集定義約束容差集合差異度，直接計算不完備數據對象集合內所有對象的總體相異程度，以不完備數據聚類的結果為基礎進行缺失數據的填補，優化了缺失數據的填補效果。陳靜杰等［20］通過計算QAR（Quick Access Recorder）數據樣本之間的標準歐氏距離選擇最近鄰樣本，利用熵值賦權法計算最近鄰的加權系數，基于最近鄰樣本中燃油流量的加權平均即可得到缺失燃油流量的估計值，有效插補了飛機油耗的缺失數據。Daberdaku等［21］使用特征之間的最大信息系數（Maximal Information Coefficient，MIC）作為距離計算的權重，整合患者自身和患者之間的信息。獨立測試線性插值和加權KNN插補算法為每個特性選擇最佳的插補方案，通過組合它們進行最終插補，使重癥監護室患者多次就診的縱向臨床實驗室檢測結果的插補效果更顯著。陳帥等［22］通過發掘插補過程中非缺失數據的低秩特性，借助奇異值分解理論建立了魯棒性更強的SVD?KDR（Singular Value Decomposition? Known Data Regression）算法模型，有效減弱了缺失數據對參數估計精度的不利影響，所提算法在高缺失率下仍具有較高插補精度和穩健性。

上述插補算法可以對不同情況的缺失數據進行估計，得到較為準確的插補。但是，由于沒有解決維度災難問題，即使是經過插補的高維特征缺失數據，聚類效果也表現不佳。

為了解決維度災難問題，需要對高維數據進行降維處理。對數據的降維過程需要滿足兩個基本條件：一是數據的維度應該減少；二是需要有效地辨別數據中突出或隱藏的特性。將目標數據集中的數據點按行排列得到由原始數據集構成的數據矩陣，從代數的角度分析，降維可看作是將原始數據點集構成的數據矩陣分解為兩個因子矩陣相乘的過程。矩陣分解法［12］即可以對原始數據矩陣進行分解，得到對應的兩個低維的數據矩陣，從而實現對原始數據的降維。矩陣分解的過程中，目標數據點集丟失的信息較少，可以較好地保留目標數據中所包含的特征信息，因此可以利用矩陣分解法來學習高維數據集的子空間結構。利用子空間進行聚類可以解決高維數據的維度災難問題，但是在學習數據子空間結構時，會受到插補信息的影響，當插補信息不適合時，得到的子空間結構用于聚類表現不佳。因此，本文針對高維特征缺失數據提出一種新的插補聚類算法，該算法相較于其他插補聚類算法更加適合聚類分析。

2 面向高維特征缺失數據的KISC算法

2.1　高維特征缺失數據的插補聚類問題

2.2　KNN插補子空間聚類框架

KNN插補算法［23］是一種面向機器學習任務的被廣泛使用的數據插補算法。將KNN插補算法用于處理高維特征缺失數據時，由于維度災難問題和數據缺失導致的樣本間距離度量方法失效問題，無法進行有效插補，從而導致聚類效果不佳。為了解決上述問題，本文結合KNN插補算法和子空間聚類算法的優點，提出一種面向高維特征缺失數據的KNN插補子空間聚類算法KISC。該算法的基本思想是：在潛在子空間下，同類數據距離相近，異類數據距離較遠，求出高維特征缺失數據的子空間結構可以解決樣本間的距離度量失效的問題；同時，低維結構也能解決維度災難問題，改善高維特征缺失數據的聚類效果。算法的框架如圖1所示。

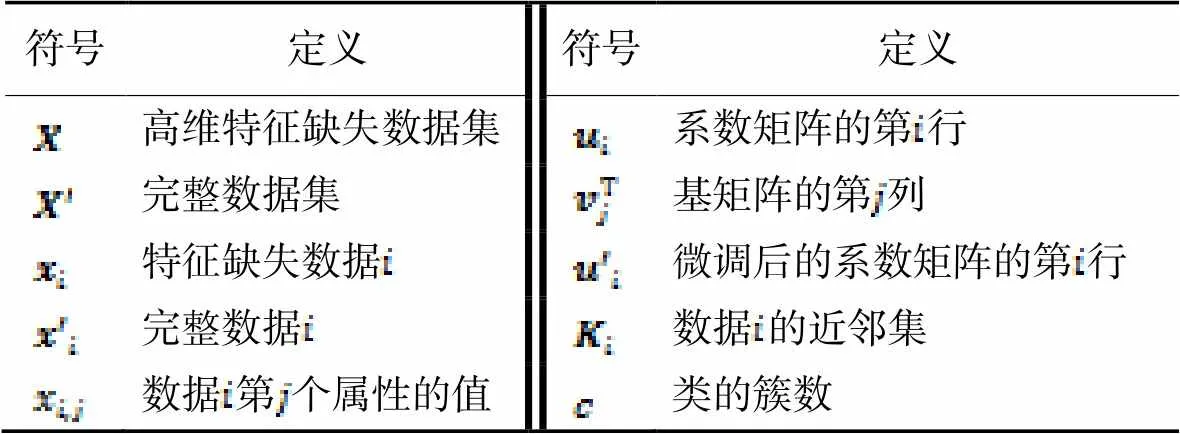
表1　符號與定義

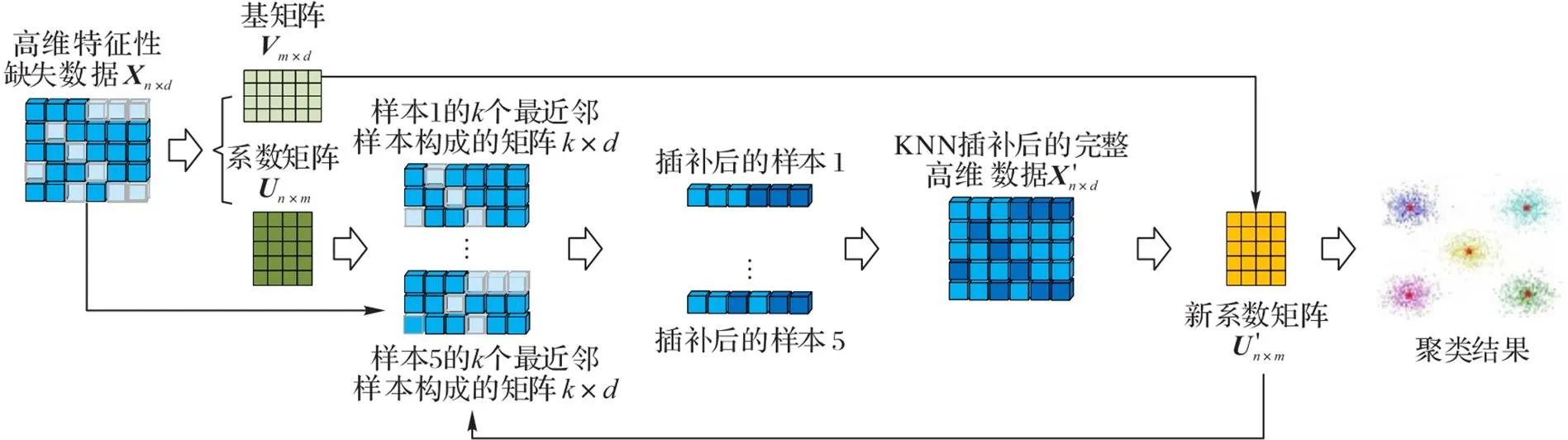
圖1　KISC算法框架

算法的核心步驟如下：

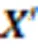
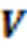
2.3　矩陣分解過程

首先使用矩陣分解算法學習高維特征缺失數據的子空間結構，分解公式如下：

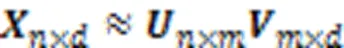
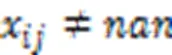
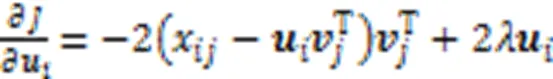
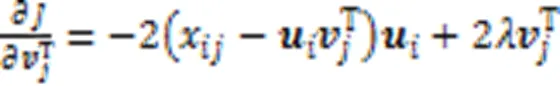
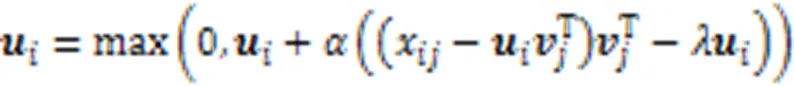
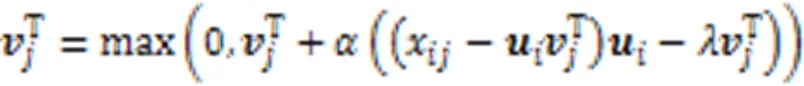
2.4　插補過程

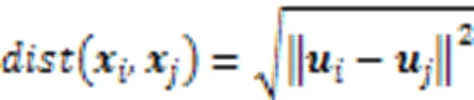
利用式（7）求出子空間下所有數據之間的距離，從而可以得到缺失數據的近鄰樣本構成的近鄰集。為了不被插補的數據誤導，本文在插補過程中加入一個約束條件，即：只使用原始數據集中的數據信息進行插補。

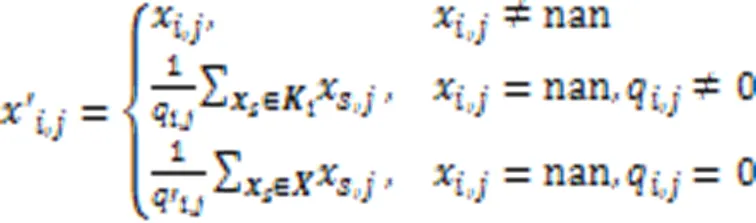
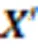
2.5　KNN插補子空間聚類算法

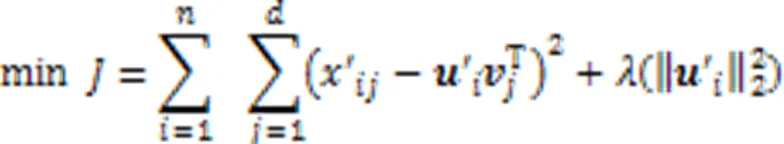
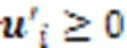
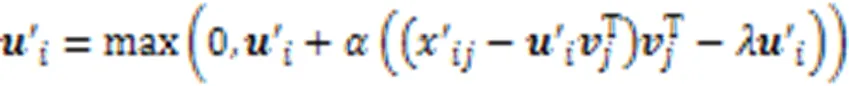
學習高維特征缺失數據的子空間結構，可以在子空間下挖掘出數據間的近鄰關系，從而解決KNN算法在高維和特征缺失情況下不能計算數據間有效距離的問題。同時，本文固定子空間的基矩陣，充分利用插補信息對子空間的影響，多次迭代KNN插補和矩陣分解過程，逐漸調整數據子空間的系數矩陣，使高維特征缺失數據的子空間結構更加穩定可靠，得到更好的聚類結果。KISC算法的具體流程如下：

根據式（7）計算所有數據間的有效距離；

end

3 實驗與結果分析

3.1　實驗數據

為了驗證本文所提算法的有效性，本文選取了6個不同規模的高維數據集。數據集的詳細描述如表2所示。

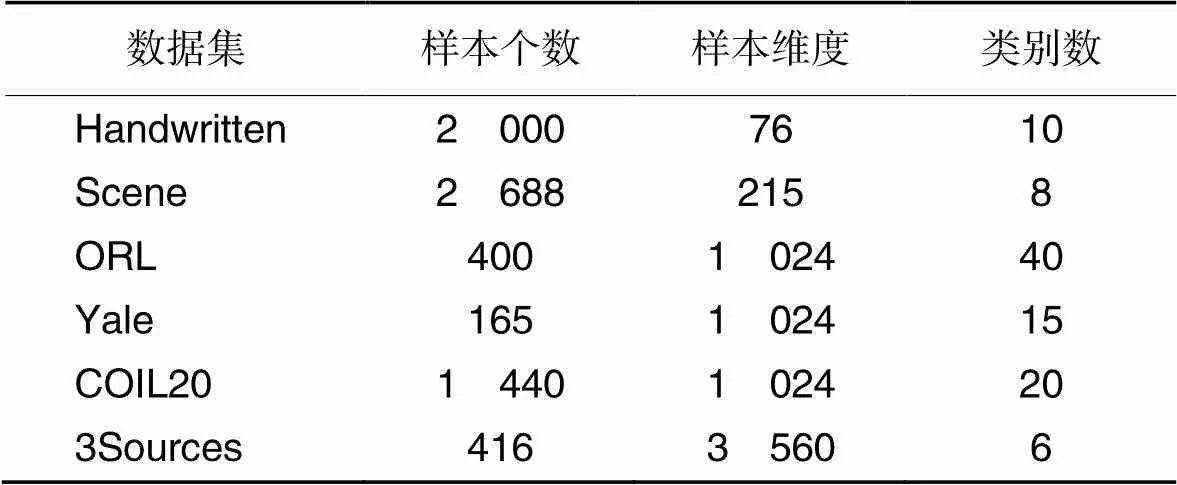
表2　數據集描述

3.2　實驗設置

本文實驗都是在3.6 GHz CPU，8 GB內存，Windows 10操作系統下完成的，本文算法采用Matlab2018b實現。

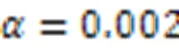
將實驗對比過程分為兩部分：

1）為了證明子空間聚類的有效性，使用0值插補法、最大值插補法、最小值插補法、均值插補法、KNN插補法、EM插補法、矩陣分解（Matrix Factorization， MF）一次插補法共7種插補算法將高維特征缺失數據補全后，直接在數據的原始空間進行聚類分析，并與KISC算法進行比較。

2）為了驗證本文算法KISC學到的子空間更適合高維特征缺失數據的聚類分析，使用以下算法與KISC進行比較：①基于統計學的對比算法，包括0值插補法、最大值插補法、最小值插補法、均值插補法、EM插補法。利用這些插補算法將高維特征缺失數據補全后，對完整數據進行矩陣分解得到高維數據的子空間結構，并在該子空間結構進行聚類。②基于機器學習的對比算法，包括KNN插補法、MF法和MF一次插補法。MF法直接使用矩陣分解算法學習高維特征缺失數據的子空間結構，并使用學習到的子空間結構進行聚類。MF一次插補法是在MF法的基礎上利用子空間下的近鄰關系補全高維特征缺失數據，再次使用矩陣分解學習完整數據的子空間結構，不對子空間進行調整，直接利用子空間進行聚類。MF一次插補法與本文算法KISC的區別在于：直接使用完整數據首次矩陣分解得到的子空間進行聚類，不對子空間結構進行調整。

3.3　評價指標

本文使用的評價指標為標準互信息（Normalized Mutual Information， NMI）和聚類精確度（ACCuracy， ACC）［26］。

3.4　實驗結果分析

表3和表4列出了對比算法在6個圖像數據集原始空間的聚類性能。結果表明：相較于經過插補后直接進行聚類的對比算法，本文的KISC算法聚類效果更好，這說明子空間結構能夠更加容易且有效地識別數據的潛在聚類結構。

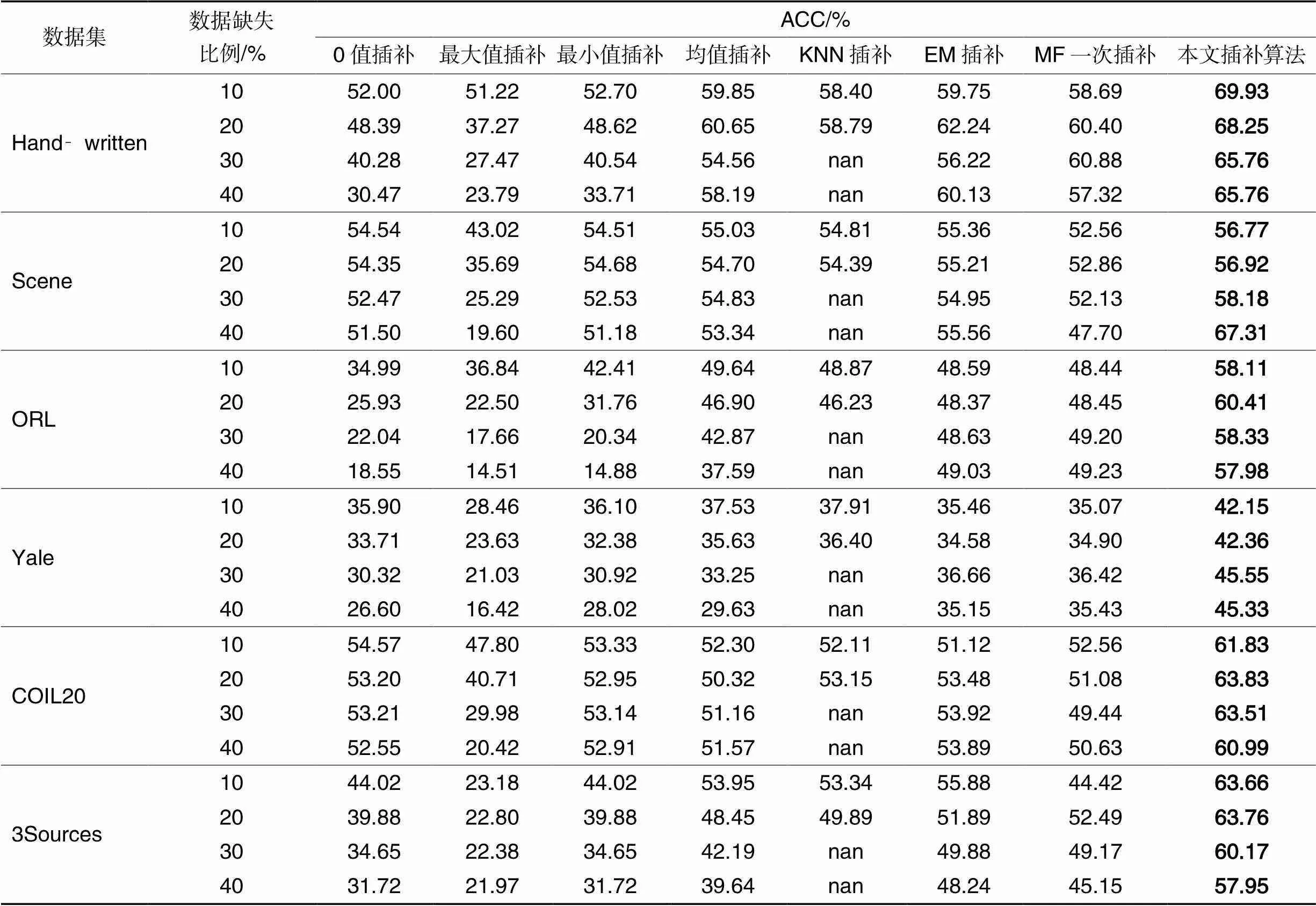
表3　在原始空間聚類結果的ACC值比較

表5和表6列出了對比算法在6個高維數據集子空間下的聚類性能。根據聚類效果，可以得出如下結論：

1）在缺失率相同的條件下，0值插補、最大值插補、最小值插補的聚類效果并不穩定，而其他對比算法的聚類效果相對穩定。缺失率為10%時，0值插補和最小值插補在Scene和3Sources數據集上的聚類效果與其他對比算法相近，在其余數據集上的聚類效果相對較差，這與高維特征缺失數據的結構存在聯系。當缺失率增加時，0值插補、最大值插補、最小值插補受到很大影響，聚類效果變化較大，而其他對比算法的聚類效果變化小。這說明不同插補信息會對高維特征缺失數據的潛在聚類結構造成不同程度的影響，使用數據的整體信息進行插補聚類，不僅可以改善聚類效果，而且加強了算法的魯棒性。

2）在算法相同的條件下，不同缺失率的數據對算法的影響不同。MF算法在處理低缺失率數據時，聚類性能與其他對比算法相近，但是當缺失率高于30%時，MF算法的聚類效果急劇下降。說明數據缺失率較高時，只使用已知數據信息不易學到缺失數據的潛在聚類結構。0值插補、最大值插補、最小值插補的聚類性能隨著缺失率的增加逐漸下降，這三種方法沒有利用樣本之間的全面信息，導致插補數據極大程度地扭曲了高維特征缺失數據的潛在聚類結構，缺失率越高，對聚類結構的破壞越大。KNN插補算法的聚類效果相對較好，但是，當數據缺失率過高時，每條數據都會存在不同程度的缺失，無法滿足KNN插補算法所需條件，所以該算法部分聚類結果用nan（空值）表示。均值插補、EM插補、MF一次插補和KISC算法使用樣本之間的全面信息進行插補聚類，聚類效果較好，并且受缺失率改變的影響較小。

3）KISC算法在各個數據集的聚類性能均優于均值插補、KNN插補和EM插補算法，說明KISC可以更有效地利用數據之間的聯系，找到高維特征缺失數據適合聚類的潛在子空間結構。同時，KISC也優于矩陣分解法和矩陣分解一次插補算法的聚類性能，表明迭代插補過程可以優化高維特征缺失數據的潛在聚類結構。本文的KISC算法在大多數據集上的NMI和ACC值都是最優的，表明它可以提升高維特征缺失數據的聚類性能。綜上所述，KISC算法更適合高維特征缺失數據的聚類分析。

表4　在原始空間聚類結果的NMI值比較

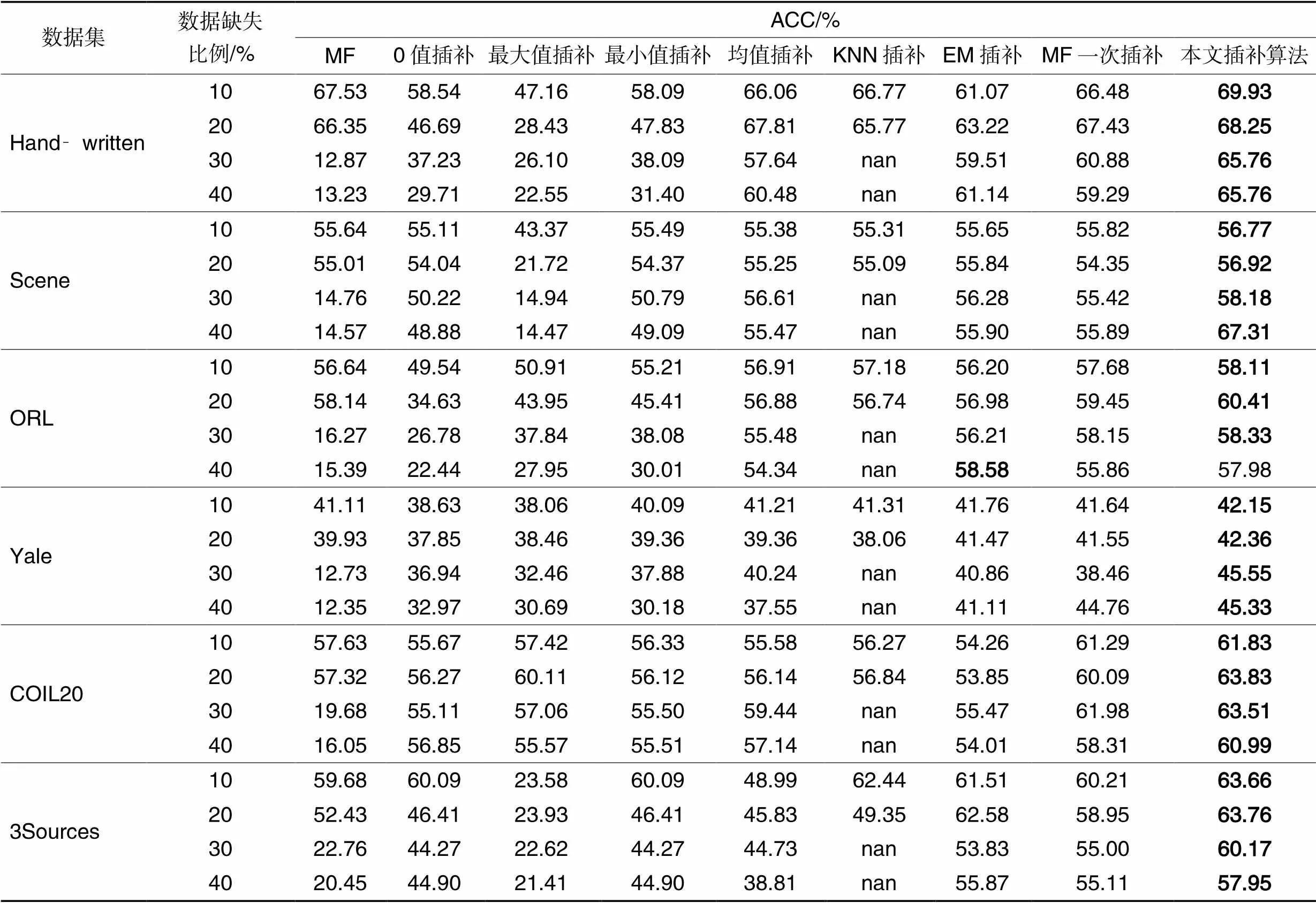
表5　不同插補算法+子空間聚類算法在子空間聚類結果的ACC值比較

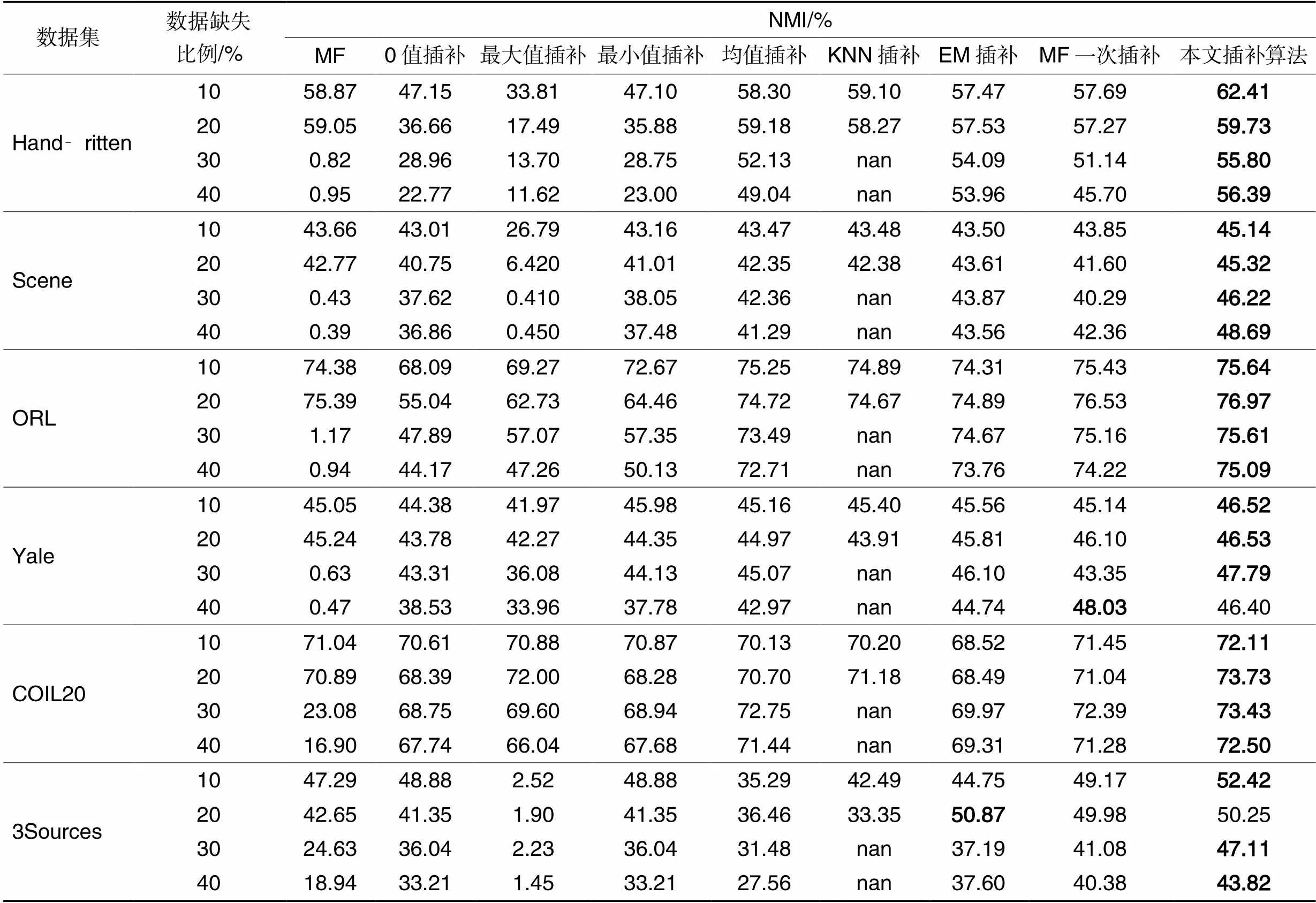
表6　不同插補算法+子空間聚類算法在子空間聚類結果的NMI值比較

3.5　模型分析

3.5.1系數矩陣的收斂性分析

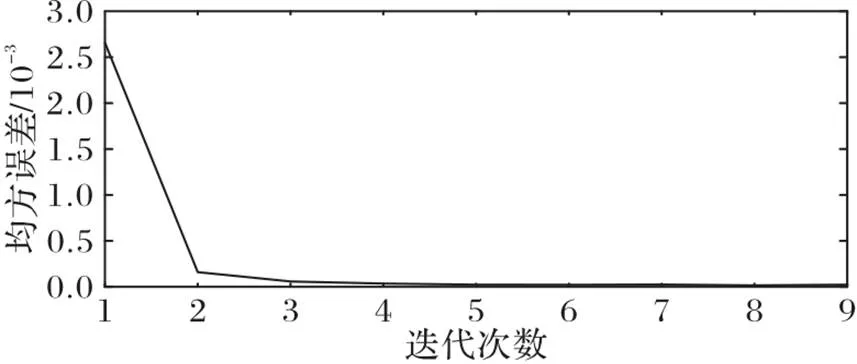
圖2　ORL數據集上缺失率為40%時，系數矩陣的變化情況

3.5.2參數分析

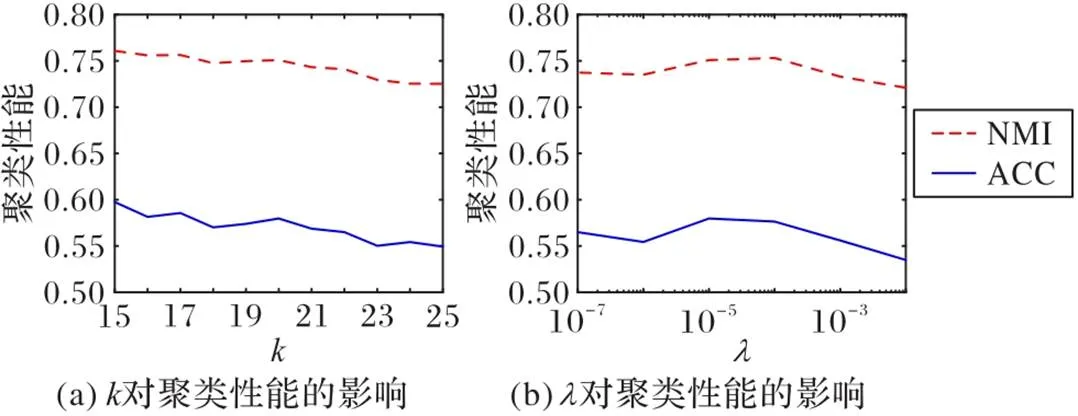
圖3　ORL數據集上缺失率為40%時，k和對聚類性能的影響

4 結語

本文針對高維特征缺失數據無法進行有效插補聚類的問題，提出一種面向高維特征缺失數據的KNN插補子空間聚類算法KISC。該算法通過學習高維特征缺失數據的子空間結構，運用子空間下的近鄰關系對缺失數據進行有效的迭代插補，并利用插補信息逐漸調整子空間結構，使子空間結構更加穩定可靠，最后使用穩定的子空間進行聚類。在不同數據集上的實驗結果顯示，該算法在NMI、ACC評價指標上的效果都有所提高，驗證了算法的有效性。然而，當缺失數據存在大量噪聲時，將缺失數據作為KNN插補子空間聚類算法的輸入可能會使聚類精度大幅降低，因此，如何識別出噪聲數據，并對缺失數據進行插補和聚類，需要被進一步研究。

[1] CHEN L F， JIANG Q S. An extended EM algorithm for subspace clustering［J］. Frontiers of Computer Science in China， 2008， 2（1）： 81-86.

[2] ERT?Z L， STEINBACH M， KUMAR V. Finding clusters of different sizes， shapes， and densities in noisy， high dimensional data［C］// Proceedings of the 3rd SIAM International Conference on Data Mining. Philadelphia， PA： SIAM， 2003： 47-58.

[3] WU X D， KUMAR V， QUINLAN J R， et al. Top 10 algorithms in data mining［J］. Knowledge and Information Systems， 2008， 14（1）： 1-37.

[4] MULLER K R， MIKA S， RATSCH G， et al. An introduction to kernel?based learning algorithms［J］. IEEE Transactions on Neural Networks， 2001， 12（2）： 181-201.

[5] LUXBURG U von. A tutorial on spectral clustering［J］. Statistics and Computing， 2007， 17（4）： 395-416.

[6] VIDAL R. Subspace clustering［J］. IEEE Signal Processing Magazine， 2011， 28（2）： 52-68.

[7] LUSCOMBE N M， GREENBAUM D， GERSTEIN M. What is bioinformatics？ a proposed definition and overview of the field［J］. Methods of Information in Medicine， 2001， 40（4）： 346-358.

[8] RAJENDRAN P， MADHESWARAN M. Hybrid medical image classification using association rule mining with decision tree algorithm［J］. Journal of Computing， 2010， 2（1）：127-136.

[9] BEEFERMAN D， BERGER A. Agglomerative clustering of a search engine query log［C］// Proceedings of the 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2000： 407-416.

[10] SHI J B， MALIK J. Normalized cuts and image segmentation［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000， 22（8）： 888-905.

[11] SHEPITSEN A， GEMMELL J， MOBASHER B， et al. Personalized recommendation in social tagging systems using hierarchical clustering［C］// Proceedings of the 2008 ACM Conference on Recommender Systems. New York： ACM， 2008： 259-266.

[12] LEE D D， SEUNG H S. Learning the parts of objects by non? negative matrix factorization［J］. Nature， 1999， 401（6755）： 788-791.

[13] KALTON G， KISH L. Some efficient random imputation methods［J］. Communications in Statistics ― Theory and Methods， 1984， 13（16）： 1919-1939.

[14] DEMPSTER A P， LAIRD N M， RUBIN D B. Maximum likelihood from incomplete data via the EM algorithm［J］. Journal of the Royal Statistical Society： Series B （Methodological）， 1977， 39（1）： 1-22.

[15] LITTLE R J A， RUBIN D B. Statistical Analysis with Missing Data［M］. 2nd ed. Hoboken， NJ： John Wiley & Sons， Inc.， 2002：200-220

[16] 金勇進. 缺失數據的插補調整［J］. 數理統計與管理， 2001， 20（6）： 47-53.（JIN Y J. Imputation adjustment for missing data［J］. Journal of Applied Statistics and Management， 2001， 20（6）： 47-53.）

[17] 熊巍，潘晗，劉立新. 穩健高效的高維成分數據近似零值插補方法及應用［J］. 統計研究， 2020， 37（5）： 104-116.（XIONG W， PAN H， LIU L X. Robust efficient imputation of rounded zeros in high?dimensional compositional data and its applications［J］. Statistical Research， 2020， 37（5）： 104-116.）

[18] LUX T C H， WATSON L T， CHANG T H， et al. Interpolation of sparse high?dimensional data［J］. Numerical Algorithms， 2021， 88（1）： 281-313.

[19] 武森，馮小東，單志廣. 基于不完備數據聚類的缺失數據填補方法［J］. 計算機學報， 2012， 35（8）： 1726-1738.（WU S， FENG X D， SHAN Z G. Missing data imputation approach based on incomplete data clustering［J］. Chinese Journal of Computers， 2012， 35（8）： 1726-1738.）

[20] 陳靜杰，車潔. 基于標準歐氏距離的燃油流量缺失數據填補算法［J］. 計算機科學， 2017， 44（6A）： 109-111， 125.（CHEN J J， CHE J. Fuel flow missing?value imputation method based on standardized Euclidean distance［J］. Computer Science， 2017， 44（6A）： 109-111， 125.）

[21] DABERDAKU S， TAVAZZI E， DI CAMILLO B. A combined interpolation and weighted?nearest neighbours approach for the imputation of longitudinal ICU laboratory data［J］. Journal of Healthcare Informatics Research， 2020， 4（2）： 174-188.

[22] 陳帥，趙明，郭棟，等. 基于SVD?KDR算法的工業監測數據插補技術［J］. 機械工程學報， 2021， 57（2）： 30-38.（CHEN S， ZHAO M， GUO D， et al. Missing data imputation using SVD? KDR algorithm in industrial monitoring data［J］. Journal of Mechanical Engineering， 2021， 57（2）： 30-38.）

[23] GARCíA?LAENCINA P J， SANCHO?GóMEZ J L， FIGUEIRAS? VIDAL A R， et al.nearest neighbours with mutual information for simultaneous classification and missing data imputation［J］. Neurocomputing， 2009， 72（7/8/9）： 1483-1493.

[24] 項亮. 推薦系統實踐［M］. 北京：人民郵電出版社， 2012： 64-72.（XIANG L. Recommender System Practice［M］. Beijing： Posts and Telecommunications Press， 2012： 64-72.）

[25] DEZA M M， DEZA E. Distances and similarities in data analysis［M］// Encyclopedia of Distances. 2nd ed. Berlin： Springer， 2013： 291-305.

[26] XU W， LIU X， GONG Y H. Document clustering based on non? negative matrix factorization［C］// Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York： ACM， 2003： 267-273.

K?nearest neighbor imputation subspace clustering algorithm for high?dimensional data with feature missing

QIAO Yongjian1， LIU Xiaolin1，2， BAI Liang1，2*

（1，，030006，；2（），030006，）

During the clustering process of high?dimensional data with feature missing， there are problems of the curse of dimensionality caused by data high dimension and the invalidity of effective distance calculation between samples caused by data feature missing. To resolve above issues， a K?Nearest Neighbor （KNN） imputation subspace clustering algorithm for high?dimensional data with feature missing was proposed， namely KISC. Firstly， the nearest neighbor relationship in the subspace of the high?dimensional data with feature missing was used to perform KNN imputation on the feature missing data in the original space. Then， multiple iterations of matrix decomposition and KNN imputation were used to obtain the final reliable subspace structure of the data， and the clustering analysis was performed in that obtained subspace structure. The clustering results in the original space of six image datasets show that the KISC algorithm has better performance than the comparison algorithm which clusters directly after interpolation， indicating that the subspace structure can identify the potential clustering structure of the data more easily and effectively； the clustering results in the subspace of six high?dimensional datasets shows that the KISC algorithm outperforms the comparison algorithm in all datasets， and has the optimal clustering Accuracy and Normalized Mutual Information （NMI） on most of the datasets. The KISC algorithm can deal with high?dimensional data with feature missing more effectively and improve the clustering performance of these data.

high?dimensional data; feature missing; imputation algorithm; subspace structure; clustering

This work is partially supported by National Natural Science Foundation of China （62022052）， Shanxi Basic Research Program （201901D211192）， “1331 Project” Quality and Efficiency Improvement Construction Program of Shanxi Province.

QIAO Yongjian， born in 1995， M. S. candidate. His research interests include missing data clustering.

LIU Xiaolin， born in 1990， Ph. D. candidate. Her research interests include machine learning， clustering analysis.

BAI Liang， born in 1982， Ph. D.， professor. His research interests include clustering analysis.

1001-9081（2022）11-3322-08

10.11772/j.issn.1001-9081.2021111964

2021?11?19；

2021?11?29；

2021?12?06。

國家自然科學基金資助項目（62022052）；山西省基礎研究計劃項目（201901D211192）；山西省“1331工程”提質增效建設計劃項目。

TP391

A

喬永堅（1995—），男，山西臨汾人，碩士研究生，主要研究方向：缺失數據聚類；劉曉琳（1990—），女，山西太原人，博士研究生，CCF會員，主要研究方向：機器學習、聚類分析；白亮（1982—），男，山西太原人，教授，博士，CCF會員，主要研究方向：聚類分析。