貝葉斯網絡方法能為教育研究帶來什么？ ＊

顧 昕 毛夢琪 馬淑風 陳森宇

（1. 華東師范大學教育學部教育心理學系，上海 200062；2. 曼徹斯特大學健康科學學院，曼徹斯特 M13 9PL ）

一、引言

教育實證研究強調數據證據，研究者根據理論提出假設、設計實驗、收集數據、分析數據，得到支持或反對研究假設的結論。但是傳統數據分析方法在處理復雜、多元、動態的教育實證研究數據時面臨諸多挑戰。首先，隨著教育研究問題的復雜化，研究對象通常是包含多個維度、多個層次的復雜建構，傳統方法如方差分析、回歸分析等已無法滿足教育數據分析的實際需求。其次，統計分析是基于概率的推斷，具有不確定性。傳統方法得到的研究結論通常表述的是差異的顯著性或影響的大小、方向等，例如“不同家庭教養方式下的子女學業成績有顯著差異”“父母受教育程度越高，其子女學業成績越高”，這些研究結論并未體現數據證據的不確定性。再次，傳統分析流程要求預先設置被試抽樣、觀測變量、樣本容量等，得到的數據證據不可累積和更新。然而，教育是通過教師和學生的互動來實現的，學生的發展是動態的，教育數據是過程性的，模型建構是不斷變化的。動態的教育數據分析需要證據的積累與更新，需要研究結果的實時反饋。那么，是否有統計分析方法能夠處理以上問題呢？

Almond等(2015)針對教育評估中證據推理的復雜性(complexity)、不確定性(uncertainty)與動態性(dynamic)問題，提出采用基于概率推理的貝葉斯網絡(Bayesian network)方法。概率無處不在，它允許我們從不確定和不完整的數據證據中做出復雜的統計推論。對于多維度、多層次的教育數據，變量間的關系錯綜復雜，概率推理計算困難。例如在評估學生英語的聽說讀寫能力時，寫作與聽力水平依賴于閱讀能力，但是又影響著口語能力。同時，英語能力也受到學生溝通交流能力的影響，所以要評估或預測學生的聽力水平必須考慮其他能力的高低。一種簡單的處理方法是畫出變量關系的網絡圖（如圖1所示），網絡圖中的節點(node)表示變量，其連線(edge)表示變量間的依賴關系，箭頭指出的變量為“原因”變量，箭頭指向的變量為“結果”變量。這類網絡模型反映了變量間的因果關系，并能夠以貝葉斯的方式（即隨著新數據的收集而更新）表示復雜且不斷變化的信息狀態。圖靈獎獲得者Judea Pearl(1988)推廣了這類網絡模型，并稱之為貝葉斯網絡。

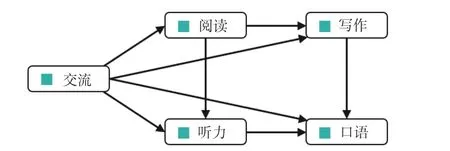
圖1 貝葉斯網絡示例(Almond等, 2015)

貝葉斯網絡使用圖形表達變量間的復雜關系（圖1)，變量關系既可以根據理論設定，也可以由數據信息給出。從這一點來說，貝葉斯網絡模型同教育與心理學實證數據分析常用的路徑分析模型與結構方程模型(侯杰泰等, 2004)十分相似。然而貝葉斯網絡和其他使用類似圖形結構的模型之間存在幾點區別。首先，貝葉斯網絡無需假定變量間的線性關系，特別適用類別變量的非線性關系建模(Gupta &Kim, 2008)。其次，貝葉斯網絡依據概率來報告變量狀態，適合診斷與預測(Sinharay, 2006)。更重要的是，貝葉斯網絡能夠隨著數據的收集而更新(Reichenberg, 2018)，這意味著，數據證據可以積累或改變。研究者可以得到更多的數據證據支持研究理論，也可能有新的數據證據反對研究理論。數據證據的更新不依賴于實驗設計，模型中任意變量數值的改變都將對整個模型產生影響。

目前貝葉斯網絡已廣泛應用于各個研究領域，包括計算機科學、統計學、認知科學、心理學、教育學等。在教育學領域，貝葉斯網絡的應用主要涉及：（1）學生發展的動態監測，García等(2007)使用貝葉斯網絡診斷并監測學生的學習風格；Carmona等(2008)設計動態貝葉斯網絡構建學生學習風格模型；Sabourin等(2013)利用動態貝葉斯網絡構建自主學習的早期預測模型。（2）不同維度的數據證據整合，Belland等(2017)將貝葉斯網絡用于STEM教育中的認知數據證據整合；De Klerk等(2015)利用貝葉斯網絡對教育心理學數據測量做了系統性評估。（3）復雜研究問題的模型構建，Pietro等(2015)在高等教育研究中使用貝葉斯網絡評估教師表現，同時考慮內部績效指標以及學生需求、期望、滿意度等外部指標；Xenos (2004)在開放與遠程教育中使用貝葉斯網絡評價學生表現，構建了多變量關系的復雜模型；Mouri等(2016)使用貝葉斯網絡預測大學生學業成績。（4）在教育與心理測量領域的應用，Reichenberg (2018)綜述了教育與心理測量中使用貝葉斯網絡的文獻，并關注其應用；Almond等(2015)展望了貝葉斯網絡在教育測評中的應用。在國內的教育實證研究中，同樣出現了許多貝葉斯網絡的應用研究，主要集中在教育評價(張曉勇等, 2012; 柳炳祥等, 2018; 張戈輝, 2018)，認知診斷與自適應學習(宋麗紅, 2016; 閆志勇等, 2002)等領域。但是，目前還未見有文章從教育實證研究的角度介紹貝葉斯網絡的方法與應用，也未見有研究系統地論述貝葉斯網絡方法與模型在教育實證研究中的特征與優勢。

本文論述教育數據分析的貝葉斯網絡方法與模型，闡述貝葉斯網絡與傳統實證研究方法在研究范式、數據分析、統計模型等方面的不同與優勢，介紹貝葉斯網絡的基本算法與實現軟件，結合具體的教育實證研究案例展示貝葉斯網絡方法的應用。

二、什么是貝葉斯網絡

貝葉斯網絡是一種以概率方式描述變量之間關系的圖模型(Pinto等, 2009)，由有向無環圖（directed acyclic graph, DAG）和條件概率表（conditional probability table, CPT）兩部分組成。其中DAG中的節點表示變量，節點間的有向連線表示變量間的因果關系。若兩個節點間以一個單箭頭連接在一起，則箭頭指出的是父節點(parent node)，表示“原因”；箭頭指向的是子節點(child node)，表示“結果”。例如圖1中，閱讀指向寫作，因此閱讀為寫作的父節點，寫作為閱讀的子節點。

貝葉斯網絡使用條件概率表儲存所有節點在其父節點下的條件概率，若無任何父節點則儲存其邊緣概率（即不依賴于其他節點變量的概率）。需要注意的是，任意一個變量在給定父節點的情況下都獨立于它的非子節點，這有助于變量的評估與預測。例如在圖1英語測試中，給定閱讀能力時，聽力與寫作能力是獨立的，在評估寫作能力時，我們僅需考慮寫作在閱讀和交流能力下的條件概率。根據貝葉斯網絡的鏈式法則，所有變量的聯合概率分布可以簡化為每個節點關于其父節點的條件概率的乘積。每個節點的邊緣概率等于每個節點的條件概率乘以其父節點的條件概率直至最上方的父節點的邊緣概率（即最終的“原因”）。以英語能力測試為例，將測試結果簡化為兩個狀態：高分或低分（記為1或0），圖2展示了其中交流、寫作、閱讀三個能力變量間的網絡結構模型。用P(寫作)表示寫作得高分的概率，P(閱讀)表示閱讀得高分的概率，P(交流)表示交流得高分的概率。此外，交流是閱讀的父節點，交流得高分的學生在閱讀上能得高分的概率表示為P(閱讀|交流)。同樣地，交流和閱讀都得高分的學生在寫作上能得高分的概率表示為P(寫作|閱讀,交流)。那么，可以從圖中變量間的依賴關系推出P(閱讀)=P(閱讀|交流)×P(交流)以及P(寫作)=P(寫作|閱讀,交流)×P(閱讀|交流)×P(交流)。在收集到學生三項能力測驗表現后，可得交流能力的邊緣概率并計算出閱讀、寫作能力的條件概率表，建立完整的貝葉斯網絡模型。

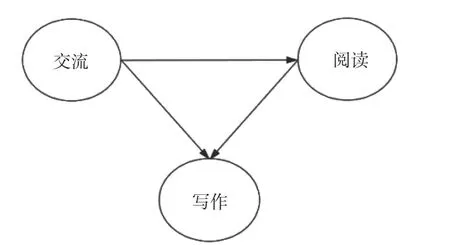
圖2 貝葉斯網絡推理示例

貝葉斯網絡可以進行因果推理(causal inference)，目標變量在給定其他變量狀態時的概率作為推理依據。具體地，目標變量及其父節點、子節點和子節點的其他父節點共同組成了該變量的馬爾可夫毯（Markov Blanket），提供所有的概率依賴信息。利用這些概率信息，貝葉斯網絡可以實現從原因到結果的推理，從結果到原因的推理，同一結果不同原因的關聯推理，以及包含以上三種的混合推理等。在英語測試的例子中，當數據更新學生交流和閱讀的表現后，可預測其寫作能力高的概率（原因到結果）；當知道學生的寫作和閱讀表現后，可反推其交流能力高的概率（從結果到原因）；當知道學生的寫作表現后，可推理交流和閱讀的關系（關聯推理）。對因果推理感興趣的讀者可參考Pearl(2009)。

貝葉斯網絡結構中的變量依賴或獨立關系可以從圖的角度進一步討論。在網絡圖DAG中，d分離(d-separation)提供了一種方法快速確定任意一對變量之間是否條件獨立(Pearl, 1988; Geiger, Verma& Pearl, 1990)。考慮三個節點A，B和C，A和B通過C間接連接的情況有三種：匯連(converging connection)、順連(serial connection)、分連(diverging connection)，如圖3所示。匯連結構也被稱為V結構，變量C能夠誘發A和B之間的信息流動，A和B之間邊緣獨立，但以C為條件時，A和B之間條件依賴。這種結構類似回歸模型，如家庭環境A與學校環境B共同影響學生行為C，家庭環境和學校環境邊緣獨立，但當考慮學生因素時，條件依賴。在順連和分連結構中，變量C將阻塞A和B之間的信息流動，A和B之間邊緣依賴，但以C為條件時，A和B之間條件獨立。順連結構類似中介模型，如家庭社會經濟地位A通過子女社會文化觀C間接影響子女的創造力B，家庭社會經濟地位與子女創造力相關，但在子女社會文化觀不變時，家庭社會經濟地位和子女創造力條件獨立。分連結構又稱為共同原因模型，如教育雙減政策C提升了教師滿意度A與家長滿意度B。

圖3 節點之間的三種基本結構

三、貝葉斯網絡能為教育實證研究帶來什么？

前文介紹了貝葉斯網絡模型與方法，本節具體討論貝葉斯網絡相較于傳統方法的優勢，能解決哪些傳統方法不能解決或不能很好解決的問題。

（一）理論驅動與數據驅動的融合

隨著人工智能、大數據分析的發展，國內外研究者開始關注數據驅動的教育學研究(Kurilovas,2020; 孟志遠等, 2017; 楊現民等; 2020)，但也有學者重申理論驅動的教育研究的重要性(Huang & Hew,2018; 楊向東, 2014)。理論驅動的分析流程是“研究問題—提出假設—設計實驗—收集分析數據—驗證假設”，研究者需要理論構建模型，表達變量間的關系。數據驅動的分析流程是“研究問題—收集分析數據—得出結論”，研究者直接根據獲得的所有數據信息構建模型，省去了研究假設與實驗設計。

下面以農村地區學生學業困難的影響因素為例（Mandinach, 2012），具體說明兩種傳統分析路徑的差異與缺點，并闡述融合理論與數據驅動的貝葉斯網絡方法的優點。理論驅動分析方法首先根據研究問題提出研究假設，影響學業困難的因素有家庭狀況、健康狀況、不良行為等。再確定抽樣對象、樣本容量及觀測變量，包括因變量學習成績，自變量家庭收入、醫療記錄、違紀頻率等。隨后收集數據，使用線性回歸模型分析以上自變量是否對學習成績有顯著的影響及影響大小，驗證研究假設。這一分析流程存在兩個缺陷。首先，理論假設可能忽略某些對學業困難有顯著影響的重要變量，如班主任管教方式，一旦確定研究設計、收集數據后無法增加新的觀測變量。其次，需要事先設定樣本容量的大小，樣本不足會導致假設檢驗失效，而樣本過多則會提高實驗成本。

數據驅動分析流程首先明確研究問題，研究者試圖了解為什么部分學生會在學業上遇到困難。隨后收集到學生學業成績、醫療記錄、行為數據、出勤率等，以及其他看似與學業困難不相關的變量，如當地交通、當地氣候等。基于所有數據信息，利用相關分析、聚類分析等大數據分析常用方法，得到學業困難的相關因素。注意，所有觀測到的數據信息都可以加入分析。數據驅動方法的缺點是僅能判斷與學業困難相關的變量，無法解釋它們的影響機制。如研究者發現學生學業困難與當地氣候有關，但真實原因可能是惡劣天氣導致交通不便，進而影響學生學業。

貝葉斯網絡結合理論驅動與數據驅動的思想，其基本分析流程可歸納為：“研究問題—先驗模型—收集分析數據—階段性結論—更新模型—收集分析數據—”。首先，貝葉斯網絡可以整合特定教育研究領域內的理論知識與專家經驗。貝葉斯方法鼓勵專家（教育學者、一線教師等）參與選取變量并定義變量間的關系，這種關系可以是相關也可以是因果。比如，指定當地氣候影響交通，進而影響學業困難的路徑。專家經驗將作為先驗知識加入貝葉斯網絡模型，這意味著先驗模型的結構將有教育理論支撐，也能適應特定的研究目的。其次，在先驗模型構建之后，研究者收集分析數據，得到階段性結論，并更新先驗模型，再收集分析數據，以此迭代。基于這一流程，貝葉斯網絡能夠從教育數據中學習。貝葉斯網絡的數據學習特性來源于貝葉斯公式，其反映了人們對過去的認知會隨著新數據的加入而發生改變。當收集到新的數據時，貝葉斯網絡將改進基于教育理論或專家經驗的原始模型，或更新之前數據分析得到的歷史模型。這種學習既可以調整模型參數，也可以對模型結構提出更改建議。后者對于教育研究是有指導意義的，因為它反映了不斷積累的數據證據對教育理論或專家經驗的批判性修正。比如，隨著小康社會的全面建成、農村經濟的整體發展，家庭收入、交通狀況或不再是影響學業困難的主要因素，而學業壓力等可能成為新的影響因素。因此，新研究數據的分析結果會動搖我們對過去的認知。需要注意的是，部分數據分析結果往往不足以推翻舊的理論，但是貝葉斯模型會降低歷史模型的可信度，直到積累足夠的數據證據反對歷史模型。

綜上，相較于傳統理論驅動或數據驅動分析方法，貝葉斯網絡融合理論與數據信息構建模型，隨著新數據的收集迭代模型，更新研究結論。貝葉斯網絡方法避免了理論驅動方法在假設模型提出后無法增加新的變量，在實驗設計后無法增加樣本容量，在得到結論后無法更新修正等問題；同時，貝葉斯網絡方法彌補了數據驅動方法在解釋變量因果關系、影響機制等方面的不足。

（二）概率推理

基于概率推理的教育實證研究結果具有不確定性，這種不確定性來自研究抽樣誤差、測量誤差、統計分析誤差等。傳統統計推斷報告的研究結論通常是變量存在“顯著差異”“顯著相關”“顯著影響”等，研究者無法知曉其所關心變量，如學生能力、教師水平等高低的概率。貝葉斯網絡將概率推理的不確定性納入模型。概率可以用來表示個體發展、預測信息、情景感知以及數據和先驗知識融合等不確定性。研究者根據理論設定貝葉斯網絡初始模型時，將這些不確定性帶入模型，當數據輸入后，利用概率迭代進行推理，推理的結論同樣以概率表示。

以網絡教學中的學生學習風格推理為例（García等, 2007），學習風格包括信息加工、感知、輸入和理解等維度。其中，信息加工有兩種類型：活躍型與沉思型，根據學生在網絡學習論壇和聊天室中的不同行為表現推理其信息加工的類型。論壇變量包括四種狀態：回復消息、閱讀消息、發布消息、不參與；聊天變量包括三種狀態：參與、聆聽、缺席。研究者評估學生信息加工風格，對于類別變量的關系，傳統統計方法常使用交叉表格卡方檢驗，但是其得到的結論只能是信息加工風格與論壇、聊天等變量獨立或顯著相關；或是使用二元邏輯回歸模型，但是其只能判斷論壇、聊天等變量是否顯著影響信息加工風格。而貝葉斯網絡方法除了構建模型表達變量間的關系，還能對學生個體的信息加工風格進行概率推理。比如García等（2007）構建了圖4的貝葉斯網絡，并根據數據生成變量的條件概率表1。若觀測到某學生在論壇回復消息且參與聊天，則由表1可推理其信息加工風格為活躍型的概率為0.85；若觀測到另一位學生僅在論壇中閱讀消息并且沒有參與聊天，則可推理其信息加工風格為沉思型的概率為0.55。與傳統統計推斷方法得到的變量顯著相關、顯著影響等結論相比，貝葉斯網絡更關注個體層面的概率推理，得到的結論更加精準有效。

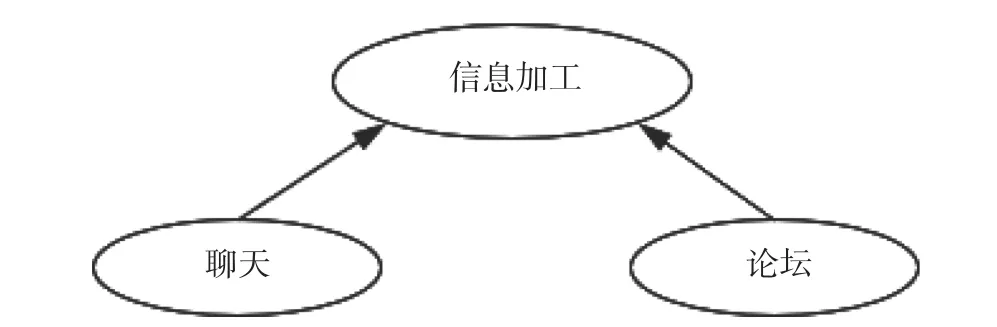
圖4 信息加工的貝葉斯網絡

表1 信息加工風格條件概率表

（三）復雜模型構建

教育研究問題往往涉及多變量、多維度的復雜建構。為了處理變量間的復雜關系，教育數據分析大多采用中介與調節模型（溫忠麟等, 2005）、結構方程模型（侯杰泰等, 2004）、多水平模型（馬曉強等,2006）等。但是這些模型都有很強的數據假設，如正態性、模型殘差隨機、獨立、齊次等，在處理類別變量的非線性關系時，會有較大的估計誤差，導致模型診斷與預測效果不佳(Gupta & Kim, 2008)。此外，這些模型能夠處理的變量關系復雜度有限，擬合具有較高復雜依賴性的數據是一項挑戰(Almond等,2015)。貝葉斯網絡對數據類型與變量關系類型都沒有要求，連續或類別變量、正態或非正態數據都可以納入貝葉斯網絡模型；線性或非線性的變量關系都可以在貝葉斯網絡模型中表達與分析。同時，作為大數據分析方法，貝葉斯網絡能夠處理多維度、多層次的復雜變量關系。

在前文例子中，研究者診斷學生學習風格，考慮信息加工、感知、理解維度(García等, 2007)。每個維度有兩種類別，分別為活躍型與沉思型、感悟性與直覺型、序列性與綜合型，由學生的網絡學習行為數據診斷。研究中的信息加工、感知、理解均為類別變量，不滿足傳統線性回歸模型、中介模型等的正態性、方差齊次、線性等假設。圖5構建了學習風格的貝葉斯網絡，研究者根據聊天行為、考試提交時間、修改答案行為、考試結果等變量診斷學生個體的學習風格。此外，在圖5中貝葉斯網絡可將學習風格模型的各維度分塊建模，再對學習風格模型整體進行評估，分析信息加工、感知與理解維度間的關系。

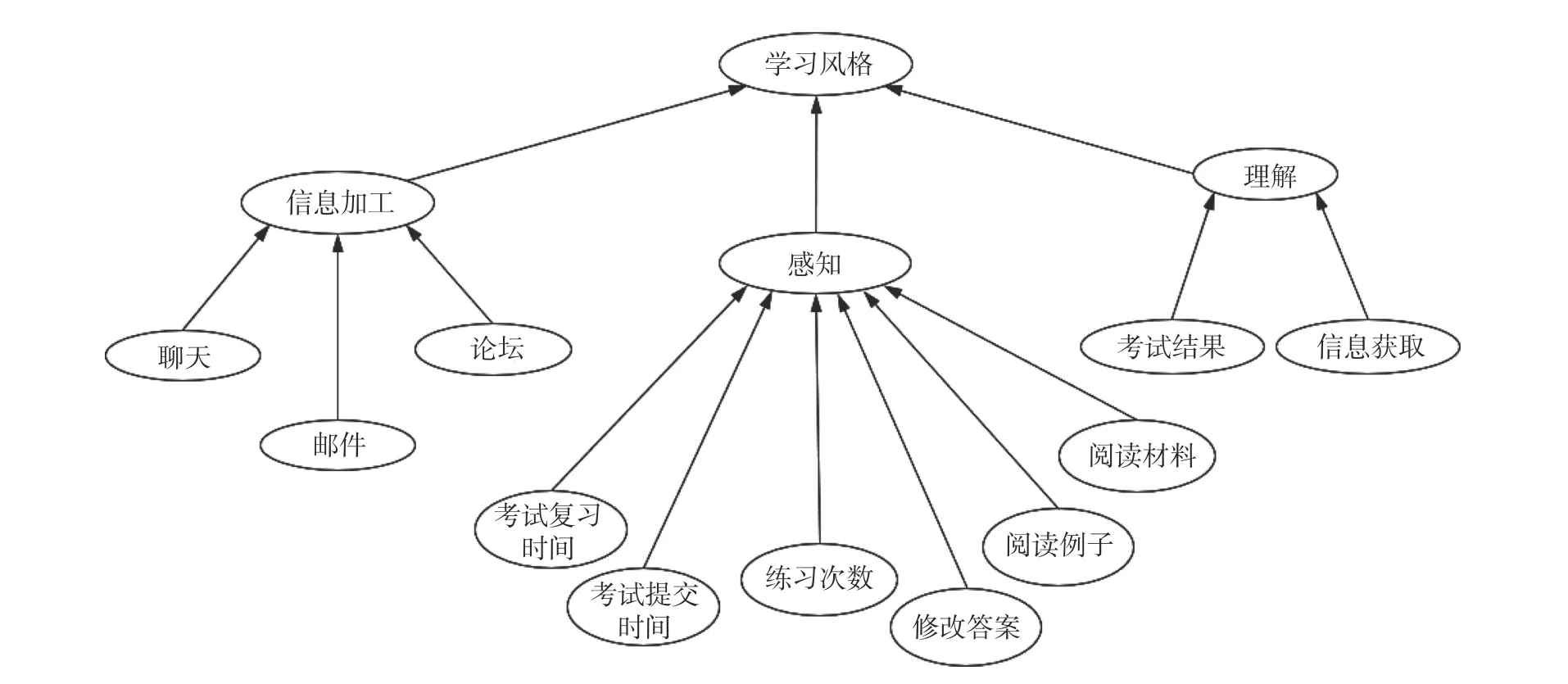
圖5 學習風格的貝葉斯網絡(García等, 2007)

（四）實時監測與反饋

傳統教育測評多以紙筆測驗為主，計算測驗問卷的總分或平均分。這類評估通常指向知識、技能的單一維度，無法進行多維度、多層面的復雜測評。同時，如果問卷包含較多題目，或者學生沒有意識到問卷的用途，往往會不經過仔細思考隨意選擇答案，得到的結果可能是不準確的。此外，傳統測評獨立于教學與學習活動，強調終結性評價，無法獲知學生在學習過程中的發展與變化。當前教育研究關注過程性評價，以真實學習情境為載體，智能設備與系統為工具，教育過程數據為證據，動態測評模型為方法，實時監測與反饋為目標，評估學生在學習過程中體現出來的知識、技能、方法、思維、風格和價值觀念等。隨著便攜式視頻設備、智能學習系統引入課堂，學生在教學活動過程中的多維、動態數據可被捕捉，如教師教學時學生的面部表情，小組討論中學生的發言次數，課堂練習中學生點擊智能設備的頻率等。基于教育過程數據在真實課堂中評價學生的能力，能夠幫助教師全面、即時地了解學生的發展狀況，從而更好地建立學習提升計劃。

傳統動態數據分析方法是建立時序模型，即將變量進行時間分割后加入模型，如重復測量模型、縱向追蹤模型、自回歸模型、交叉滯后模型(Grimm等, 2021)等。這類模型分割的時間是離散的，需要在某一時刻觀測到所有變量數據信息才能更新模型。但是教學與學習過程是連續的，行為數據并非發生在某一特定時刻；換句話說，特定時刻可能觀測不到研究者需要的行為信息，因此這類時序模型無法做到實時監測與反饋。貝葉斯方法的天然優勢就是處理數據的動態更新。教育研究者根據理論或專家經驗等設置初始模型后，每當數據進入，模型都將更新，支持或反對研究理論的數據證據也持續累積。值得注意的是，在某一時刻，貝葉斯網絡不需觀測模型中的所有變量即可完成更新。例如，在數學課堂學習中，捕捉到學生舉手發言后，我們對其注意力、計算思維等能力的評估，以及數學成績的預測也將隨之發生改變。貝葉斯網絡能夠有效融合動態學習過程中的所有數據信息，從而幫助教師評估學生知識、能力等的薄弱環節，實現實時監測和反饋。此外，貝葉斯網絡還能夠綜合歷史數據，推測學生發展趨勢，為教師調整教學方案提供參考。

以前文學生學習風格與其在網絡教學中的互動行為關系為例（García等, 2007），研究者可以建立重復測量模型，構建學習風格與互動行為的動態關系。例如在學習開始時、中間某時刻、結束時，分別收集學生的聊天、論壇、郵件等行為數據，構建學習風格的重復測量模型，評估學生學習風格在三個時刻的變化趨勢。但是，重復測量模型等傳統時序模型局限于固定時刻變量關系的多次評估，無法做到學習風格的實時評估。為此，García等（2007）構建了學習風格與互動行為的貝葉斯網絡模型，分析學生在使用網絡教學系統時的學習與互動過程數據（見圖5）。模型構建與數據分析是連續的動態過程，在任意時刻，學生的任何行為，如參與聊天、回復郵件等，都將更新模型，給出學習風格的最新概率推理結果。換句話說，監測學生學習風格不需設置特定時間節點，不需觀測所有行為數據。因此，貝葉斯網絡相較于傳統時序模型，能夠提供實時監測。

（五）小樣本、缺失與不完整數據分析

受限于人力、物力、經費等實驗條件，教育實證研究的樣本容量可能相對較小。例如，教育神經科學研究需要對被試進行腦紅外成像或核磁共振，能收集到的樣本有限。在參數估計方面，對小樣本數據使用傳統極大似然法（Maximum likelihood）估計變量間的相互關系，極易受到個別極端數據的影響，產生有偏差的估計結果。貝葉斯方法融入基于專家經驗或歷史數據的先驗信息，減小了極端值的影響，比極大似然法的估計精確度更高（Van de Schoot等, 2017）。在假設檢驗方面，頻率統計方法需要確定樣本容量、顯著性水平等。實際操作中研究者可能會因為樣本容量較小，無法得到任何結論，也可能會收集過多的樣本數據造成浪費。貝葉斯方法無需預先設定樣本容量，不依賴于實驗設計，對多次實驗可以進行數據證據的積累。即使一次實驗的樣本較小，無法得到有用的結論，研究者也可以繼續收集新的數據，在貝葉斯模型中積累數據支持研究假設的證據，直到得到有意義的教育研究結論。一般來說，貝葉斯統計分析所需的樣本容量都小于頻率統計分析，而貝葉斯網絡繼承了貝葉斯統計方法在小樣本參數估計和假設檢驗方面的優勢。

教育研究數據可能存在缺失或不完整的情況，例如因為實驗設備問題造成的部分學生的視頻或音頻數據缺失。對于缺失與不完整數據，貝葉斯網絡同樣比傳統方法表現更優。貝葉斯網絡模型可根據變量間的相互依賴關系計算各變量的條件概率，比如當學生聽力水平高的概率是80%時，即使其口語能力測驗數據缺失，我們也可根據其聽力水平對口語能力進行估算。在具體分析中，貝葉斯網絡使用期望最大化(Expectation-Maximum)算法從不完整數據中估計條件概率。與其他估計方法不同，無論數據是隨機缺失或是缺失依賴于其他變量的狀態，期望最大化算法都可以處理缺失值的估算。

本節重點闡述了貝葉斯網絡方法較傳統數據分析方法的優勢：融合理論與數據驅動分析思想；能夠對個體進行精準概率推理；適用任何數據與變量類型；對變量多維度、多層次的復雜關系進行建模；對教育過程數據進行實時分析與反饋；不依賴樣本容量與實驗設計等。

四、貝葉斯網絡分析算法與軟件

由第2節討論可知，當知道各個變量節點的因果關系后，貝葉斯網絡的結構即可確定。但是，如果關于網絡結構的先驗信息不可知，則需要用數據驅動的方式構建網絡圖模型，即貝葉斯網絡的結構學習。目前貝葉斯網絡結構學習算法可分為三類：基于約束的算法(constraint-based algorithm)，基于評分的算法(score-based algorithm)以及兩者的混合算法。基于約束的算法主要使用條件獨立性檢驗來識別變量之間的條件獨立關系，并構造相應網絡結構圖(De Campos & Huete, 2000)，其優點是便于判斷變量間的因果關系，但是計算較為復雜。基于評分的算法使用評分函數衡量網絡模型與數據的擬合程度，將結構學習視為一個結構優化問題，利用搜索策略來選擇評分最高的結構。廣泛使用的評分指標包括模型比較常用的AIC和BIC信息準則分數。評分搜索算法的優點是給出了模型擬合數據的程度，但是當變量節點較多時，無法遍歷所有可能的模型，容易陷入局部最優。在確定結構模型后，貝葉斯網絡分析的任務是計算條件概率表，即貝葉斯網絡的參數學習。參數學習主要有極大似然估計和貝葉斯后驗估計兩種方法。這里推薦貝葉斯估計方法，與貝葉斯網絡的整體分析方法（即貝葉斯法）具有一致性，并且貝葉斯方法對于小樣本數據有較好的參數估計精度。

能夠實現貝葉斯網絡數據分析的軟件非常之多(Scanagatta et al, 2019)，這里僅介紹基于不同平臺的部分軟件，并對其算法、功能等進行比較，詳見表2。基于R語言平臺的bnlearn (Scutari, 2009)是目前使用最廣泛的貝葉斯網絡軟件，其功能強大，適用各種數據類型和結構學習算法，并能構建動態貝葉斯網絡模型，進行參數估計、模型比較和近似推理等。其他兩個R軟件包Deal和pcalg分別采用基于評分和基于約束的結構學習算法，但是均不能構建動態貝葉斯網絡模型。Banjo和Free-BN適合Java軟件使用者，BNFinder適合熟悉Python軟件的研究者，BNT適合熟悉Matlab軟件的研究者。

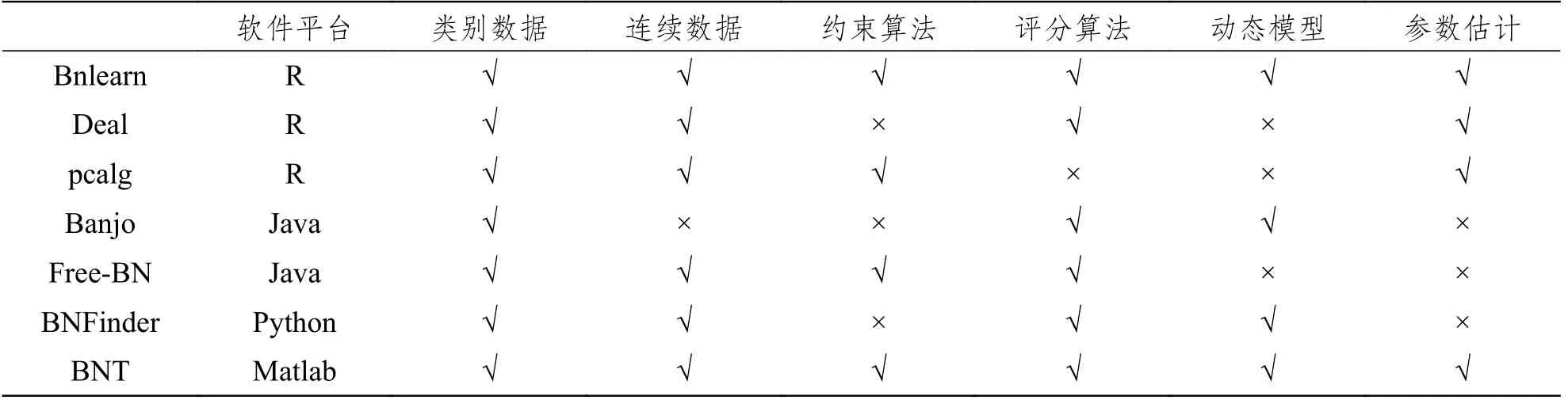
表2 貝葉斯網絡常用軟件

五、貝葉斯網絡的實證研究應用

本節使用一個教育實證研究案例來展示如何構建、分析和報告貝葉斯網絡。該實例關注青少年在合作學習過程中展現的尊重、幫助、關心、同情等親社會行為與同伴關系發生和發展的作用機制（陳森宇等, 2021）。研究收集了22名來自河北省某縣級中學的七年級學生的課堂合作學習行為視頻數據，其中男生8名，女生14名。這些學生被分為3個小組(7+7+8=22)參與基于合作推理討論（Anderson et al, 1998）的合作學習模式，每個小組進行8輪討論，其中第一次討論為正式討論前的“預演”，便于學生熟悉合作推理討論的規則和形式，之后的7輪討論作為觀察數據進行同伴互助行為的編碼，共計21次討論，討論平均時長27.5分鐘。

學生的互助行為包含討論促進行為、行為支持、認知支持、情感支持等四個大類別。其中，討論促進行為包括邀請他人發言，提醒討論規則，進一步指導等小類；行為支持表示直接回應組員的需求，提供相關學習資源等小類；認知支持包括為組員提供解釋、建議、指導，補充、評論、澄清對方觀點等小類；情感支持包括對組員給予安慰、鼓勵、關心，表達理解、尊重、親近等小類。研究在討論前與討論后測試了學生的同伴喜歡程度和同伴關系提名，前者需要學生指出是否喜歡和組內某同學一起玩（0表示不認識，1表示不喜歡，2表示喜歡），后者需要學生指出組內哪些成員被認為是他/她的好朋友（0表示不是，1表示是）。表3展示了在7輪討論中，四類互助行為出現的次數以及同伴喜歡程度和同伴關系提名次數。其中，討論促進行為在初期較多，隨著討論的進行，討論促進行為逐漸減少。行為支持略有上升，而認知支持和情感支持的變化不大。同伴關系提名次數明顯增加，同伴喜歡程度明顯上升。以上分析描述了學生互助行為與同伴關系變量的獨立變化。

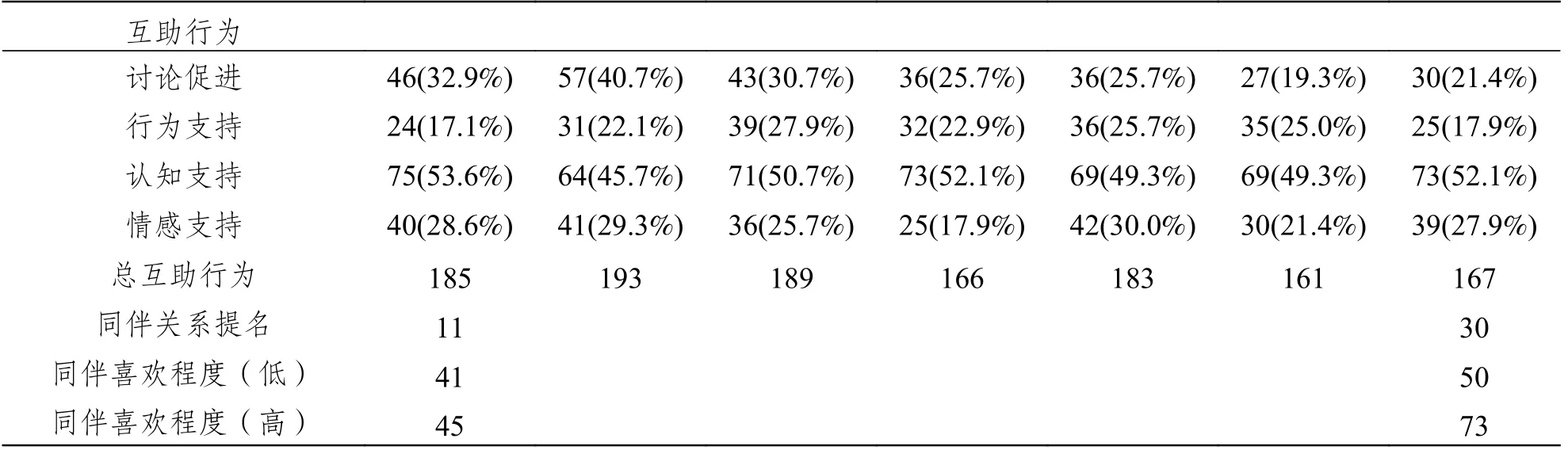
表3 學生互助行為與同伴關系統計描述表

傳統回歸分析方法的分析思路是構建因變量為同伴喜歡程度或同伴關系提名，自變量為討論促進、行為支持、認知支持、情感支持等的線性回歸模型，當模型設定后，可在T2、T3等時刻隨著討論的進行預測同伴喜歡程度或同伴關系提名的變化。但是，同伴喜歡程度或同伴關系提名在理論上是互助行為發生的內在原因，學生更有可能幫助或支持和自己關系好的組內同學。在交往和互助的過程中，具有相同或相近社會認知能力的學生更有可能發展友誼關系。因此，以同伴喜歡程度或同伴關系提名為因變量的回歸分析是不合適的。此外，該研究涉及類別變量，類別變量的數據分析是對變量發生概率的解釋和預測。使用線性回歸或邏輯回歸模型需要對類別變量進行虛擬化處理(dummy coding)，其結果的解釋較為復雜。最后，本研究的初始樣本容量較小，傳統分析方法可能無法得到任何有用的結論，也不能隨著新數據的輸入而更新數據證據。

本研究利用貝葉斯網絡構建互助行為與同伴喜歡程度和同伴關系提名的模型。為了演示簡便，模型只包含四個大類互助行為與同伴喜歡程度和同伴關系提名。在T1時刻，可獲得所有變量的觀測數據，根據先驗理論構建如圖6中T1時刻所示的貝葉斯網絡模型。圖6中的變量名下方展示了各變量的邊緣概率，例如T1時刻，同伴關系提名與否的概率分別為8%和92%，同伴喜歡程度高的概率為12%，低的概率為49%，不認識的概率為39%等。當理論模型不確定時，可計算各個備選模型的評分指標（如AIC、BIC等）進行模型比較，選擇最優的先驗模型。確定模型并帶入數據后，即可生成條件概率表，如表4所示。

在表4中，P(同伴關系提名)所在行顯示了同伴關系提名為0和1的概率。在圖6模型中，同伴關系為最上方的父節點（即最終的“因”），因此該概率為不依賴于其他變量的邊緣概率，與圖6中T1時刻同伴關系下方的概率相同。P(同伴喜愛程度)所在行展示了同伴喜歡程度為0、1、2的概率，該概率為依賴于同伴關系提名的條件概率。例如當同伴關系提名為1時，同伴喜歡程度為2的條件概率為0.884。P(討論促進)等其余行給出了四個互助行為在同伴關系提名和同伴喜歡程度給定下的條件概率。例如同伴關系提名為0且同伴喜歡程度為1時，可得認知支持為1的概率為0.544。此外，當同伴關系提名為1且同伴喜歡程度為0時，互助行為的條件概率都為默認概率0.5，這是因為該情況沒有任何觀測數據，學生提名的好朋友不會是他或她不認識的同學。

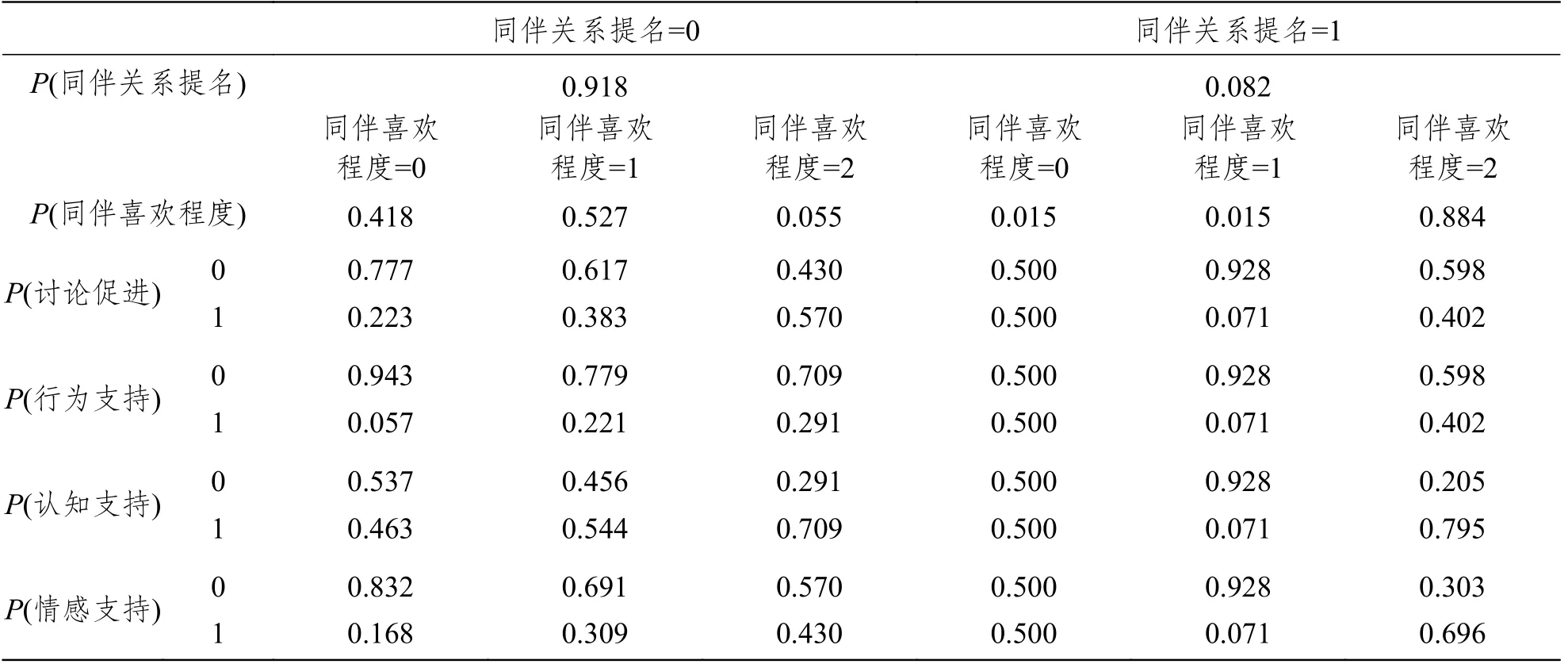
表4 T1時刻貝葉斯網絡模型條件概率表

T2到T6時刻僅能觀測學生的互助行為，但是可以利用貝葉斯網絡和條件概率表預測同伴喜歡程度與同伴關系提名。圖6中的T3和T5網絡圖為合作學習小組討論中選取的兩個時刻的預測模型，其中互助行為下方的概率為觀測值，同伴喜歡程度與同伴關系提名的概率為預測值。在T7時刻討論結束后，對學生的同伴喜歡程度與同伴關系提名再一次進行測試，新的數據用于更新模型，更新后的模型如圖6中的T7網絡圖所示，條件概率表見表5。

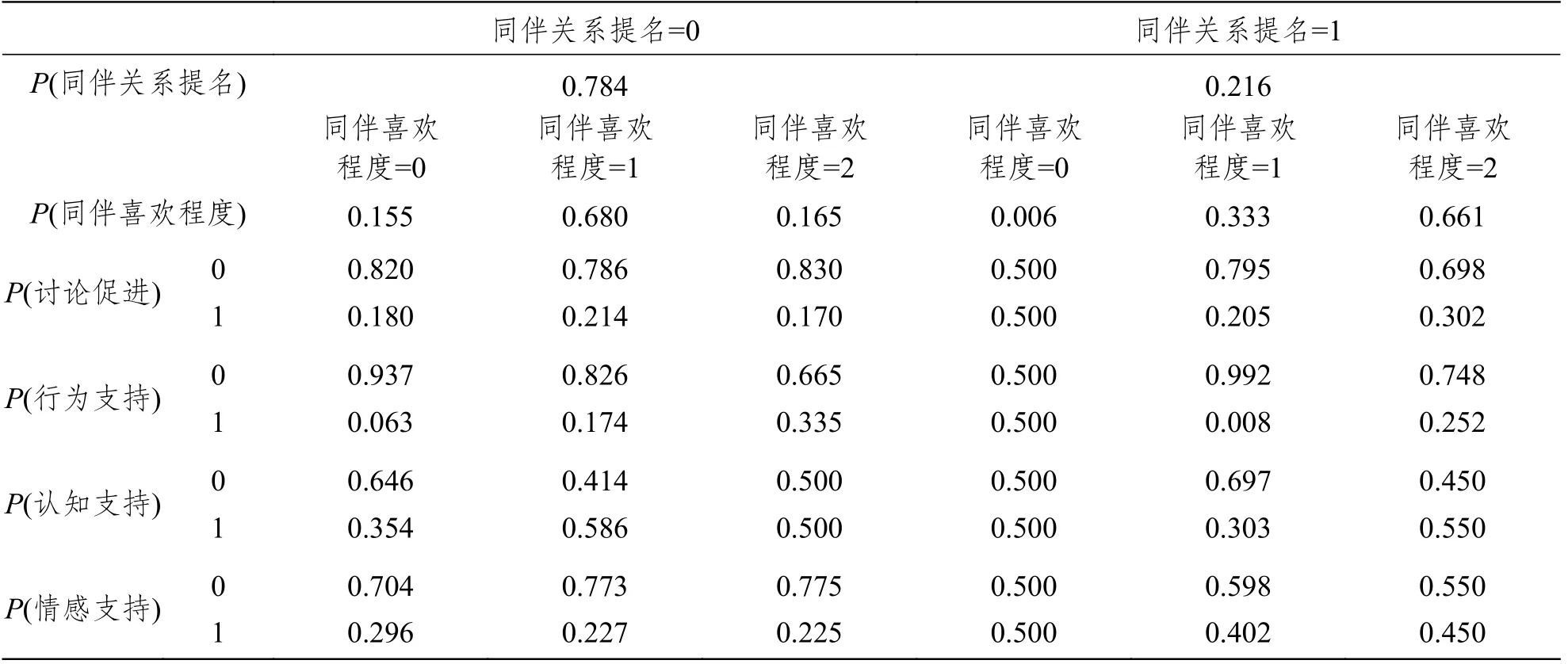
表5 T7時刻貝葉斯網絡模型條件概率表

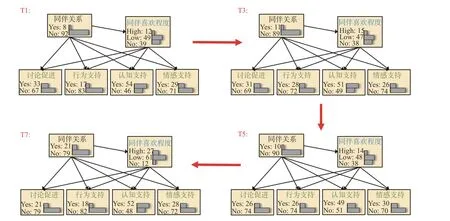
圖6 同伴關系與互助行為的貝葉斯網絡圖

當研究者沒有任何先驗知識時，可使用完全數據驅動的結構學習算法構建貝葉斯網絡模型。圖7展示了同伴喜歡程度和同伴關系提名與11個學生具體互助行為在T1時刻的網絡關系，與所有變量都無關的互助行為已被刪除。需要注意的是，完全數據驅動的模型可能無法解釋或錯誤解釋變量間的關系，如圖7中的很多互助行為并不存在因果關系，如實物幫助與給予提醒、補充評論觀點與提醒討論規則等。當新的數據不斷進入模型后，變量的關系可能會被修正，條件概率表將會更新。多次數據迭代更新后的貝葉斯網絡模型能夠準確推斷、預測變量的變化。

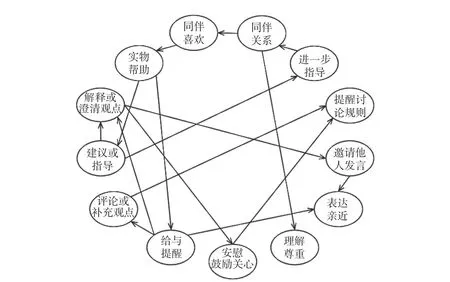
圖7 數據驅動的同伴關系與互助行為貝葉斯網絡圖

六、總結

本文闡述了貝葉斯網絡法在教育實證研究范式、數據分析方法、模型應用等方面的優勢，討論了貝葉斯網絡模型的特征、算法與軟件，通過教育研究實例展示了貝葉斯網絡模型數據分析過程。貝葉斯網絡方法已廣泛應用于眾多研究領域，但在教育實證研究中的應用相對少見。可能的原因是教育大數據研究尚處于起步階段（孟志遠等, 2017），作為大數據分析方法的貝葉斯網絡未被教育研究者所熟知。為此，本文呈現了貝葉斯網絡的基本方法與分析流程，旨在推廣貝葉斯網絡在教育實證研究中的應用。