2022年全國新高考Ⅰ卷立體幾何解答題的解法分析與復習建議

廣東 鄭燦基

一、問題呈現

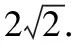
(1)求A到平面A1BC的距離；

(2)設D為A1C的中點,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.

本題以直三棱柱為背景，考查點到平面的距離、平面與平面垂直的性質定理、空間二面角等知識，著重考查邏輯推理、直觀想象、數學運算等核心素養，需要具備較好的等價轉化、推理論證、圖形分析、運算求解等能力才能很好地解決本題.

二、多維角度

(1)利用等體積法求解：

在直三棱柱ABC-A1B1C1中，設點A到平面A1BC的距離為h，則由VA-A1BC=VA1-ABC得

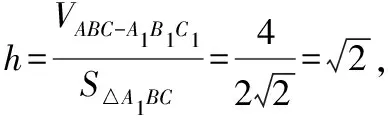
(2)解法1：法向量法.

取A1B的中點O,連接AO,如圖，因為AA1=AB，所以AO⊥A1B.

又平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B，所以AO⊥平面A1BC.

又BC?平面A1BC,所以AO⊥BC.

在直三棱柱ABC-A1B1C1中，AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC.

又AO∩AA1=A，所以BC⊥平面ABB1A1.

又AB?平面ABB1A1，所以BC⊥AB1.

所以BC，BA，BB1兩兩垂直.以B為坐標原點，BC，BA，BB1所在直線分別為x,y,z軸建立如圖所示的空間直角坐標系.

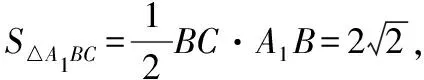
所以B(0,0,0),A(0,2,0),A1(0,2,2),C(2,0,0),D(1,1,1)，

設平面ABD的法向量m=(x1,y1,z1)，

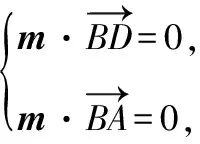
令x1=1,則y1=0,z1=-1，所以平面ABD的一個法向量為m=(1,0,-1).

設平面BDC的法向量n=(x2,y2,z2)，

令y2=1,則x2=0,z2=-1，所以平面ABD的一個法向量為n=(0,1,-1)，

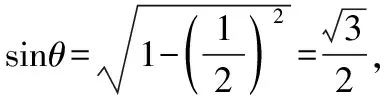
小結：向量法是求解平面與平面所成角的有力工具.求平面與平面所成角的一般思路：①建系設點：建立合理恰當的坐標系,寫出相關點的坐標;②求相關向量：求出兩個平面的一個法向量;③求向量的夾角：利用向量的數量積求出兩個法向量的夾角;④轉化：將向量夾角的余弦值轉化為二面角的余弦值.

解法2：三垂線法.

如圖，直三棱柱ABC-A1B1C1中，AA1=AB，則四邊形ABB1A1是正方形，

連接AB1，則A1B⊥AB1.設A1B∩AB1=O，

因為平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,AO⊥A1B,AO?平面ABB1A1，所以AO⊥平面A1BC.又BC?平面A1BC，所以AO⊥BC.

在直三棱柱ABC-A1B1C1中，AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC.又AO∩AA1=A，所以BC⊥平面ABB1A1.又AB?平面ABB1A1,所以BC⊥AB.

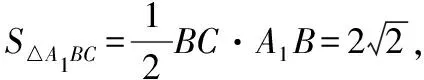
過點O作OE⊥BD于點E,連接AE.

因為AO⊥平面A1BC,所以AO⊥BD.又OE∩AO=O,所以∠AEO是二面角A-BD-C的補角的平面角.

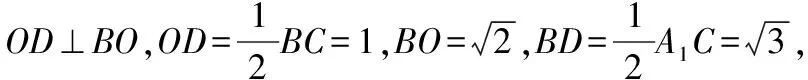
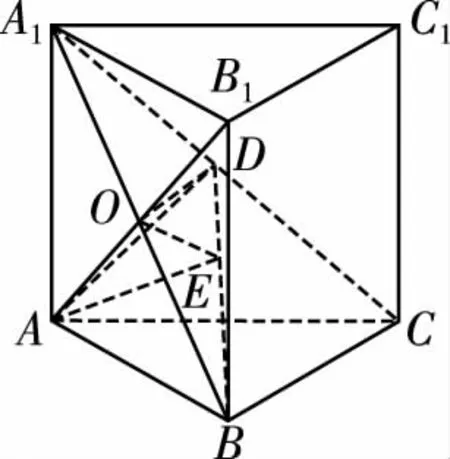
小結：利用三垂線定理及逆定理作出二面角的平面角，是傳統幾何法中解決二面角問題的重要方法之一.如圖，在二面角α-l-β中，過平面α內一點A作AO⊥平面β，垂足為O，過點O作OB⊥l于點B(過A點作AB⊥l于點B)，連接AB(或OB)，由三垂線定理(或逆定理)知AB⊥l(或OB⊥l)，則∠ABO為二面角α-l-β的平面角.我們要特別注意：①在作圖過程中，我們作出了兩條垂線AO與OB(或AB)，后連接AB兩點(或OB兩點)，這一過程可簡記為“兩垂一連”，其中AO為“第一垂線.”②“第一垂線”能否順利找到或恰當作出是利用三垂線法作二面角的平面角的關鍵.例如在本題中，AO⊥平面A1BC,A∈A1BC,所以AO是第一垂線，我們只需要過O作OE⊥BD(或過A點作AE⊥BD)于點E，連接AE(連接OE)，則∠AEO為二面角A-BD-A1的平面角即二面角A-BD-C的補角的平面角.

解法3：射影面積法.

不難看出，以上三種解法都注重對邏輯推理的考查，其中線線、線面和面面位置關系的判斷、證明以及深度挖掘，是這三種解法不可或缺的環節.如果離開了推理論證，解題思路就會受阻，難以繼續.

三、問題引申

1.求解三棱錐的體積常見的技巧策略

(1)當錐體的頂點到底面的距離不好求解，常常考慮頂點的平移：

①點在平面的平行線上平移

如圖所示，若直線l∥平面α，則直線l上所有點到平面α的距離均相等.

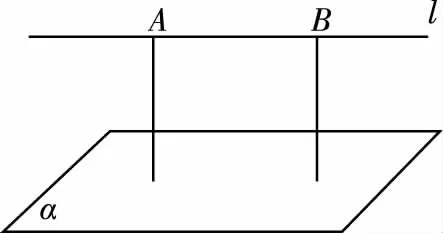
例如：如圖，當AE∥CF,則AE∥平面BCF，則VE-BCF=VA-BCF.

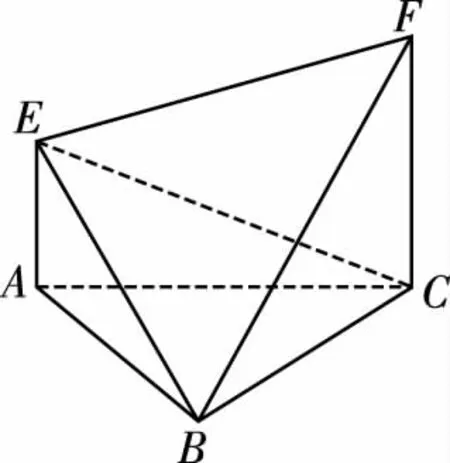
②點在與平面相交的直線上平移

如圖所示，若直線AB與平面α交于點O，則點A,B到平面α的距離之比為OA∶OB.特別地，當O為AB中點時，則A，B到平面α的距離相等.

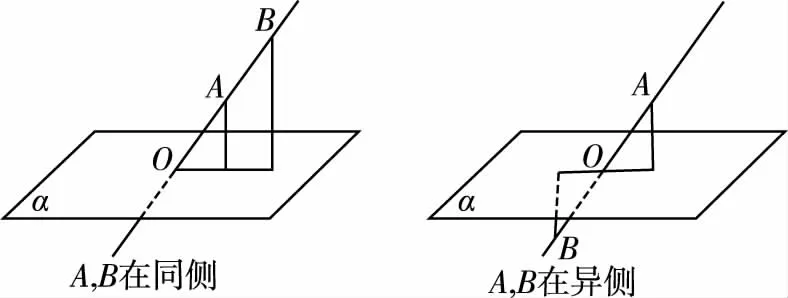
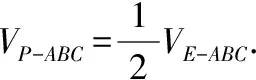
(2)求三棱錐的體積常利用等體積法進行轉化.當三棱錐的底面和高比較難求時，常常轉化為新的頂點到換得的底面的距離，容易通過題設條件進行求解.解題過程中常常靈活運用上面的方法技巧多次等價轉化.

例如：如圖，三棱柱ABC-A1B1C1中，A1D⊥底面ABC,AD=DC，側面AA1C1C為邊長為2的菱形，AC⊥CB,BC=1,求三棱錐B-A1B1C的體積.

我們可考慮這樣轉化：VB-A1B1C=VA1-BB1C=VA-BB1C=VB1-ABC=VA1-ABC.其方法是不唯一的.

又例如：(2012·遼寧文·18節選)如圖，直三棱柱ABC-A′B′C′，∠BAC=90°，AB=AC=2，AA′=1,點M，N分別為A′B和B′C′的中點，求三棱錐A′-MNC的體積.

(2)利用面面垂直的性質定理求點到平面的距離

面面垂直的性質定理是尋求點到平面的射影的重要方法，因此也是求解點到平面的距離的重要途徑.這一點在高中數學課堂中不夠重視，尤其是引進向量法后學生傾向于利用向量法求解點到平面的距離，利用面面垂直的性質定理來思考和解決問題反而被忽略了.我們來看以下例子：

(1)求證：AB⊥PC;

(2)求P到平面ABC的距離.

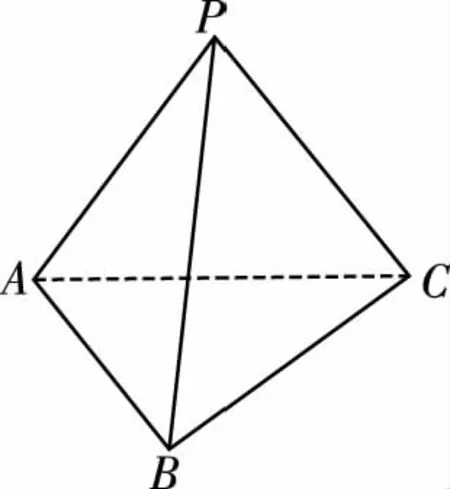
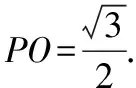
2.利用三垂線定理求二面角的平面角的技巧策略

利用三垂線定理求二面角的平面角，要遵循“作-證-求”的步驟，要善于利用圖中已有的“第一垂線”，要敢于利用已知條件和相關性質定理作出“第一垂線”.下面以一道模擬試題為例進行說明：

如圖，在四棱錐P-ABCD中，底面ABCD是菱形，PA⊥平面ABCD.

(1)求證：平面PAC⊥平面PBD.

(2)若PA=AB=2,∠BAD=60°,求二面角A-PB-D的余弦值.

第(1)問的證明不贅述.對于第(2)問，如何用三垂線法作出二面角A-PB-D的平面角呢？

思路1：如果我們利用第(1)問的結論，平面PAC⊥平面PBD，可以考慮過平面PAC內的點A作平面PBD的垂線.先尋找平面PAC與平面PBD的交線.

設AD∩BC=O，連接PO，則OP為平面PAC與平面PBD的交線.這樣我們過點A作AM⊥OP于點M，由面面垂直的性質定理可知AM⊥平面PBD.于是AM是第一垂線，過點M作直線MN垂直PB于點N，連接AN，則∠ANM就是二面角A-PB-D的平面角，如圖所示.

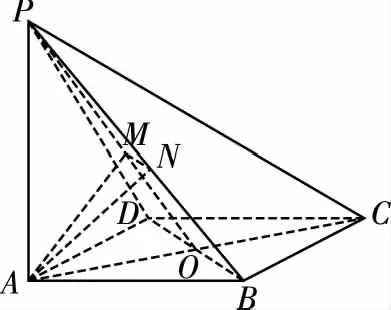
思路2：注意到平面APB和平面PBD這兩個平面中，平面APB是“豎直”的，尋找平面APB的垂線更為容易，我們可以考慮作DO⊥AB，交AB于點O.由于PA⊥DO，AB∩PA=A,所以DO⊥平面PAB，所以DO是第一垂線，過O作OF⊥PB，交PB于點F，連接DF，則∠DFO是二面角A-PB-D的平面角，如圖所示.

可以看出，利用三垂線法求二面角的方法也是有多種，我們要分析圖形特點，選擇更為恰當、有利于計算的方法，這樣可以降低計算量，達到快速解題的目的.

四、本高考題得分偏低的原因

今年高考本題的得分很低，那么問題主要是出在哪些地方？眾所周知，立體幾何是考查直觀想象能力最主要的載體，但實際有不少學生的空間觀念薄弱，對圖中點、線、面的位置關系不能識別，教師過于強調利用向量坐標法解題，都期望能借助向量坐標法較好地回避推理論證中遇到的困難，這樣容易使學生形成習慣，而缺乏對推理論證的訓練.例如2022年全國新高考Ⅰ卷的19題，如果不經過一系列推理論證說明BC⊥AB,是很難利用向量建系法解題的.因此，在學習立體幾何時一定要先掌握好基礎知識，注重傳統方法解題和邏輯推理的訓練.

五、備考建議

1.夯實基礎知識,構建知識網絡

我們要完善立體幾何中點、線、面之間的位置關系與度量關系，形成良好的數學知識體系.例如，如圖所示，空間平行和垂直是立體幾何兩個重要的問題，厘清它們之間的關聯，有助于加深對定理的理解，有利于在具體問題中靈活轉化和應用.向量法也是如此，向量法并不是幾個向量公式的套用.坐標系的建立,證明方法及計算公式的選擇,都是以幾何定義、定理為理論依據.只有夯實理論基礎，明晰概念、定理和基本方法，才能實現在更高層次上能力與技能的提升.

2.注重推理訓練，重視用傳統方法解答立體幾何解答題