一道含有全稱量詞、存在量詞的函數題易錯分析
江蘇 張啟兆 劉曉潔
函數作為高中數學內容的一條主線,對整個高中數學有著重要的意義,每年高考卷都將其作為必考題.含有全稱量詞與存在量詞的不等式成立問題,也是高考的高頻考點,考生在遇到這一部分的試題時常常出現錯誤.對此本文以2022年蘇錫常鎮四市高三教學情況調研(一)數學第12題為例,對含有全稱量詞與存在量詞的函數題中,因不理解全稱量詞與存在量詞的含義及不會等價轉化致誤的易錯點進行剖析,并提出了相應的解題策略.
一、試題呈現

【答案】AB
【解題思路】

等價于函數f(x)在(0,+∞)上沒有最小值,
【易錯:問題的等價轉化】


【易錯:不會將f′(x)轉化成適當的代數式乘積的形式】
(1)當a≤0時,當0
則當x=1時,f(x)max=f(1)=ea-1,f(x)的值域為(-∞,ea-1],f(x)在(0,+∞)內無最小值,因此,a≤0符合題意;
【易錯:忽視對參數a的分類討論】


如圖,在同一平面直角坐標系內作出直線y=a與函數y=g(x)的大致圖象.

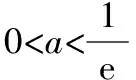
當0
即函數f(x)在(0,x1),(1,x2)上單調遞減,在(x1,1),(x2,+∞)上單調遞增,
函數f(x)在x=x1與x=x2處都取得極小值,f(x)min=min{f(x1),f(x2)},不符合題意;
【易錯:不會虛設零點x1,x2】
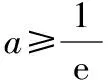
即f(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增,f(x)min=f(1)=ea-1,不符合題意.
綜上所述,實數a的取值范圍是(-∞,0],
所以滿足條件的實數a的可能值有-1,0,故選AB.
【易錯提醒】含有全稱量詞、存在量詞的同一函數的不等式成立問題,關鍵是將含有全稱量詞和存在量詞的條件“等價轉換”:
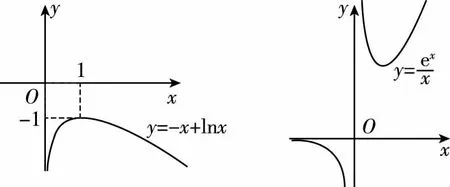
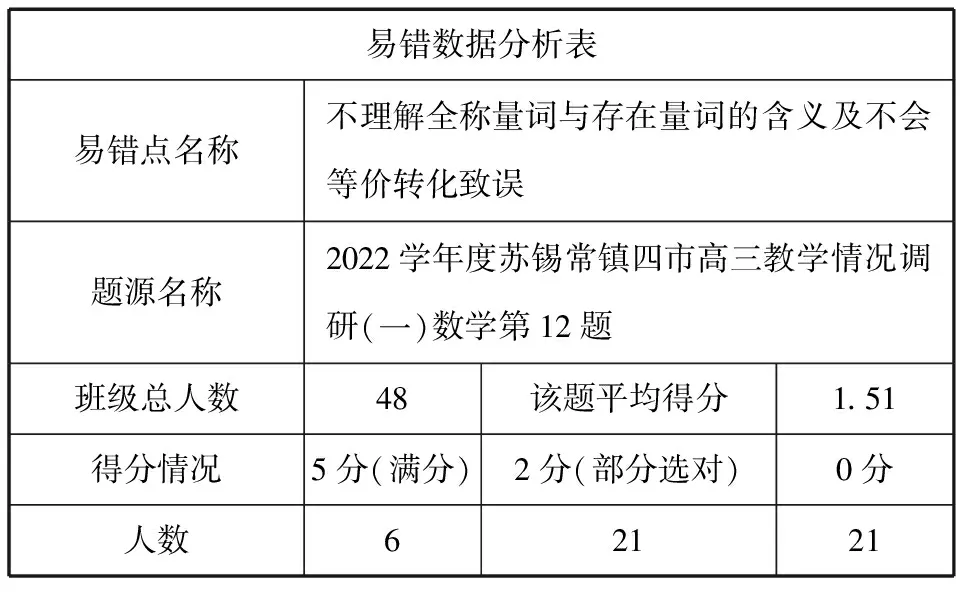
形如“對?x1∈A,都?x2∈A,總有f(x1) 形如“對?x1∈A,都?x2∈A,總有f(x1)>f(x2)成立”等價于“函數f(x)在A上沒有最小值. 問題等價于函數g(t)=at-lnt(t≥e)在[e,+∞)上無最小值. ①當a≤0時,g(t)在[e,+∞)上單調遞減,當t→+∞時,g(t)→-∞,符合題意; g(t)有最小值,不符合題意,舍去. 綜上所述,實數a的取值范圍是(-∞,0], 所以滿足條件的實數a的可能值有-1,0,故選AB. 因為?s∈(0,+∞),總?t∈(0,+∞),使得f(t) ①當a=-1時,h′(t)<0,h(t)在[e,+∞)上單調遞減,無最小值,A正確; ②當a=0時,h′(t)<0,h(t)在[e,+∞)上單調遞減,無最小值,B正確; ④當a=1時,h′(t)>0,h(t)在[e,+∞)上單調遞增,h(t)有最小值h(e),D錯誤. 解法4(檢驗法):考慮到本題是多選題中的壓軸題,對于大部分學生來說,看到本題怎樣快速搶2分,優秀學生如何快速得5分,可以使用代入檢驗法. (易錯:解題方法不靈活,不會用檢驗法) 因為求的是a的取值范圍,而給出的4個選項是具體的數值,從選擇值的判斷來說,優先選擇B,畫出函數f(x)=-x+lnx的大致圖象(如圖1),發現它不存在最小值,符合題意. 圖1 圖2 以一個班級為樣本的易錯數據分析: 易錯數據分析表易錯點名稱不理解全稱量詞與存在量詞的含義及不會等價轉化致誤題源名稱2022學年度蘇錫常鎮四市高三教學情況調研(一)數學第12題班級總人數48該題平均得分1.51得分情況5分(滿分)2分(部分選對)0分人數62121 該題是多選題的壓軸題,難度較大,從考試結果來看,得分率也極低(平均分1.51).本題以指、對數函數為載體,綜合考查導數的應用,以及含有全稱量詞、存在量詞的不等式成立問題的轉化策略,題干簡約,背景新穎,對數學抽象、邏輯推理、數學運算等數學核心素養有較高的要求.許多同學一見到此題,就感到信心不足,函數解析式中既有指數函數又有對數函數,有兩個參數,還有全稱量詞、存在量詞,做題過程中極易出錯.筆者分析主要會在以下四個方面存在問題: (1)不理解全稱量詞與存在量詞的含義,“若對于定義域內的任意實數s,總存在實數t使得f(t) (2)審題時沒有注意到本題中只有一個函數,而誤以為是兩個不同的函數,套用結論“已知函數y=f(x),x∈[a,b],y=g(x),x∈[c,d].若?x1∈[a,b],?x2∈[c,d],有f(x1) (4)不會利用分類討論、數形結合思想解決函數問題. 【解題思路】對于定義域內任意x1,總存在x2,使得f(x2) 所以函數f(x)在其定義域內無最小值, 【分析】根據給定定義可得函數h(x2)在[0,2]上的值域包含函數y=2a-x1在[0,2]上的值域,再借助a值的唯一性即可推理計算作答. 【評注】若?x1∈[a,b],?x2∈[c,d],有f(x1)=g(x2),則f(x)的值域是g(x)值域的子集. 該題重視基于數學素養的關鍵能力的考查,在數學知識層面、數學能力層面和創新思維層面都有所體現,對數學教學具有重要啟示意義. 重視基本知識和技能的學習,注重過程,讓問題探究成為課堂的中心與主線,從而拓展知識的深度,提升思維品質,培養創新意識,進一步提高素養,這是一個循序漸進的過程.布魯納曾說:“我們教一個科目,不是去建立一個有關該科目的小型圖書館,而是要學生自行思考,像一名數學家那樣去思考數學,像史學家那樣去探索歷史,投入到獲得知識的過程中去.”如果教師在準備高三數學復習課時能多在學習策略、思考方法和探索途徑上下功夫,用“問題串”驅動學生思維,促進學生深度學習,那么高三數學復習才會有“跳出題海”的希望,進而達到培養學生思維能力的目標. 今年的高考數學試題堅持“引導學校和學生減少‘死記硬背’和‘機械刷題’現象”,再一次啟發教師要轉變育人方式,重視學生的主體作用與合作探究,堅決摒棄課堂教學“滿堂灌”;重視新教材中的“拓廣探索”“探究與發現”,引導學生建立知識體系,促進學生將知識和方法內化為自身的知識結構;重視從以教為主轉向以學為主,要精準分析學情,精心設計數學探究活動;重視自主探索、動手實踐、合作交流、閱讀自學等多種學習方式,以達到提高復習效率、提升學生“四基”(基礎知識、基本技能、基本思想、基本活動經驗)的目的.



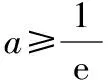
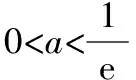


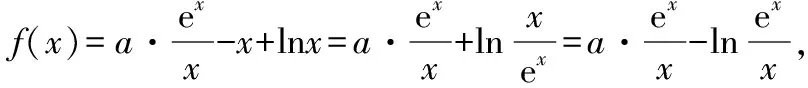
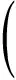




二、易錯數據
三、易錯分析
四、易錯練習

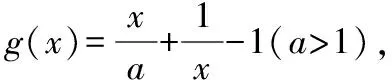
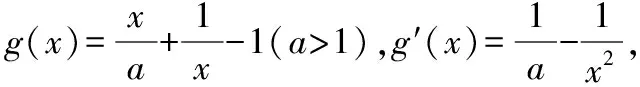


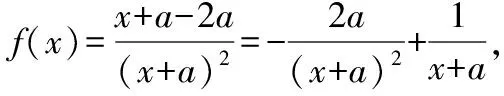
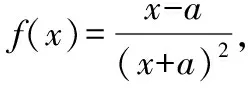






五、教學啟示
1.注重過程,提升思維品質
2.轉變角色,教為主轉向學為主
3.改變教學方式,重視主題教學、深度學習


