從一題多解到多題一解,發散思維,發展素養
——以2022年全國甲卷文科第12題為例
四川 張 君 王奮際
“雙減”背景下高考數學全國卷的命題,要求減少“機械刷題”,加強學科核心素養的考查.本文以2022年高考數學全國甲卷文科第12題為例,從一題多解著手,研究比較大小類題目的通性通法,尋求解題本質,發散數學思維,最后形成多題一解,發展數學學科核心素養.
1.真題再現
【例】(2022·全國甲卷文·12)已知9m=10,a=10m-11,b=8m-9,則( )
A.a>0>bB.a>b>0
C.b>a>0 D.b>0>a
2.試題分析
羅增儒教授把解題總結為“條件預示可知并啟發解題手段,結論預告需知并誘導解題方向”,解題的本質是找條件與結論的關系,故本題從兩種角度思考解題方案:一是綜合考慮條件與選項,做等價變形;二是直接從條件出發,推導結論.
觀察已知條件,a,b均為指數式與常數之差,作差后不易比較大小,又由于a,b無法判斷正負,作商也不易比較;再觀察選項發現,a,b都需要與0比較,故可考慮等價變形為三個對數值log1011,log910,log89的大小比較,即思路1.
等價變形為三個對數值的大小比較,此時可以直接作差(解法1),作商(解法2)比較,利用數列單調性(解法3),函數單調性比較(解法4).解法1,2,3都可以使用均值不等式將對數乘法轉化為加法,解法4則利用函數求導尋找單調性.
由于條件中的三個表達式結構類似,可以考慮構造函數,利用函數單調性比較,即思路2.此時可轉化為函數零點和單調性問題(解法5),也可轉化為兩個函數圖象分析問題(解法6),也可轉化為冪函數圖象增長速度問題(解法7).
若將9m作為整體,避開對數運算,適當放縮,轉化為尋找a的下界和b的上界的問題(解法8).
上海市特級教師文衛星老師主張以思維導圖對解題思路以形象總結,此題可表示為如下思維導圖.
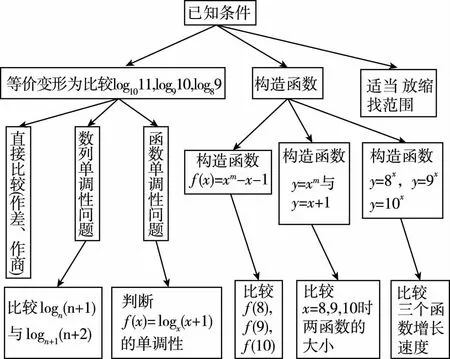
3.一題多解
3.1 思路1:綜合條件與選項,恒等變形轉化
由9m=10知m=log910,比較a=10m-11與0的大小,等價于比較10m與11的大小,等價于比較m=log910與log1011的大小;同理,比較b=8m-9與0的大小,等價于比較m=log910與log89的大小;至此,本題轉化為比較log1011,log910,log89三個數的大小.要比較這三個數又可以有如下幾種方案.

同理可證log910
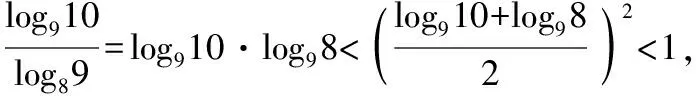
解法3:將這三個數看作數列{logn(n+1)}的第8,9,10三項,先研究數列的單調性,比較logn(n+1)與logn+1(n+2),其中n∈N,n≥2的大小.
所以ln2(n+1)-lnn·ln(n+2)>0,即logn(n+1)>logn+1(n+2).
由此可得,log89>log910>log1011,下同解法1.
點評:上述三種方法,先將對數化同底,基于同底對數沒有乘法,但可以相加,不約而同的利用均值不等式,最終完成解題.
解法4:令f(x)=logx(x+1)(x>1),則通過求導易得f(x)單調遞減.
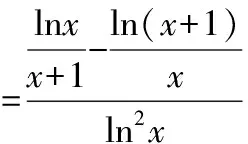

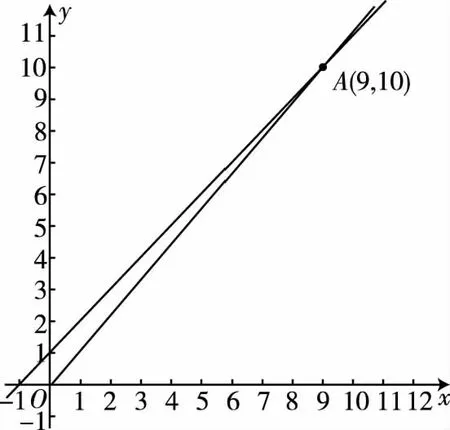
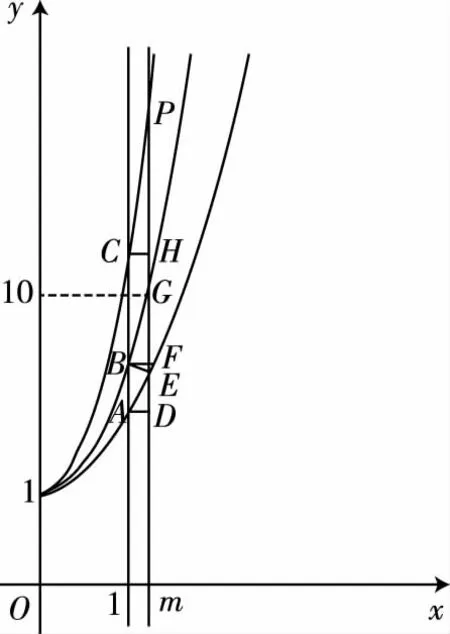
由1 所以xlnx<(x+1)ln(x+1). 因此,當x>1時,f′(x)<0,所以f(x)=logx(x+1)在(1,+∞)上單調遞減, 所以f(10) 解法5:令f(x)=xm-x-1(m=log910), 則f′(x)=mxm-1-1,令f′(x)=0, 又因為m=log910>1, 又因為f(9)=0,所以a>0>b,故選A. 解法6:f(x)=xm-x-1(m=log910), 則f(9)=0.則函數y=xm(m=log910)與y=x+1的交點為(9,10)如圖所示. 由圖可知,當0 當x>9時,xm>x+1,所以8m<9,即b=8m-9<0,10m>11,即a=10m-11>0.所以a>0>b,故選A. 解法7:如圖,從下到上分別是y=8x,y=9x,y=10x的圖象,直線x=1與三條曲線分別交于點A,B,C, 直線x=m(m=log910)與三條曲線分別交于點E,G,P, 分別過點A,B,C作x軸的平行線依次交直線x=m于點D,F,H.因為y=8x,y=9x,y=10x的圖象上升速度依次加快,則DF 所以8m-8<9m-9=1<10m-10,∴8m-9<9m-10=0<10m-11,故選A. 點評:解法4至解法7都構造了函數,但構造的函數各不相同,構造函數后,利用的函數性質也不同,可見,通法之下也有很多變化. 解法8:顯然,m>1. 所以a>0>b,故選A. 比較大小類題目是近年高考常考題,入口低,方法靈活,能全面考查學生數學思維能力.常見的方法主要有直接或變形后作差、作商比較;構造函數利用單調性比較;構造函數利用函數圖象比較;放縮法.此題中每一種通法都可以切入試題,而每種方法又不是獨立存在.通法之間可以交叉混合使用,比較log1011,log910,log89三個數不僅可以用基本不等式,還可以使用加糖不等式等方法(見5課本溯源).試題多角度、多層次進行考查,兼顧基礎性、綜合性. 事實上,比較大小的題目還可以采用估值的方法,如果考生手上有計算器,直接輸入計算即可得出答案.考場上學生要估計一個數的大小,通常可以考慮放縮法、利用常見的對數值(如lg2≈0.3,lg3≈0.477,ln2≈0.69,ln3≈1.1)、泰勒展開等. (2019年人教A版《數學必修第一冊》第141頁13題)比較下列各題中三個值的大小: (1)log0.26,log0.36,log0.46;(2)log23,log34,log45. 我們來研究一下第(2)問. 所以log23>log34. 同理可得log34>log45. 綜上所述,log23>log34>log45. 點評:作差、通分后,利用基本不等式即可判斷ln23-ln2×ln4的符號,如果掌握了這種思想方法,那么考題中a-b的符號就容易聯想到利用基本不等式來判斷,此外,課本的結論還可以推廣為logn(n+1)>logn+1(n+2)(證明見上文解法3). 這說明這道考題源于課本高于課本,因此,指導高三復習要立足課本,適當提高,就能提質減負! 國務院《深化新時代教育評價改革總體方案》提出要“改變相對固化的試題形式,增強試題開放性,減少死記硬背和‘機械刷題’現象”,這要求教學中要重視通性通法,尋找解題本質,落實核心素養. 本文對2022數學甲卷文科12題解法研究中,主要提出了三大類通法,一是綜合考慮條件和結論,等價變形后,作差、作商比較大小;二是結構相似,構造函數,利用函數性質,如單調性、圖象,增長趨勢等比較大小;三是利用放縮,特殊值,甚至泰勒展開等估計參數值的范圍比較大小. 這些“通法”當然也能遷移到其他高考題目,例如: 1.(2020·全國卷Ⅲ理·12)已知55<84,134<85.設a=log53,b=log85,c=log138,則( ) A.a C.b ∴b 點評:以上解析用到了兩種通法,a,b的比較采用作商法,b,c的比較采用放縮法. A.a C.b 所以a 點評:以上解析用到了放縮法. A.c>b>aB.b>a>c C.a>b>cD.a>c>b 點評:以上解析用到了兩種通法,b,c的比較采用作商法,b,a的比較采用構造函數的方法. 從以上三個高考題的解析可以看到,高考題強調通性通法的考查,教學中教師應注重通法的教學.學生在理解掌握通性通法之后,根據題目的具體呈現形式,靈活選擇并做適當變形,就能完成解題. 在高考題基礎上,筆者進行了一些變式,讀者可以嘗試從通法入手,完成解題. 【變式1】已知a=101.1-6,b=91.1-5,c=81.1-4,則a,b,c的大小關系是( ) A.a C.c 【變式2】已知,10m=11,a=8m-9,b=9m-10,則( ) A.a>0>bB.a>b>0 C.0>b>aD.b>0>a 【變式3】已知9m=11,a=10m-12,b=8m-10,則( ) A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a 【變式4】已知5m=31,a=6m-42,b=7m-55,則a,b,c的大小關系是( ) A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a3.2 思路2:形式同構,構造函數,逆用單調性,數形結合
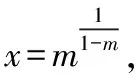
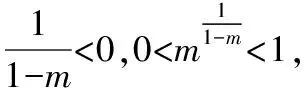
3.3 思路3:化異為同,適當放縮
4.一題多思

5.課本溯源


6.通法遷移
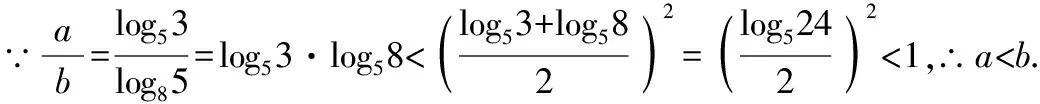
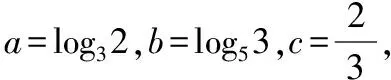
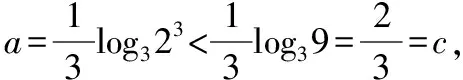


7.一題多變

