思維導圖破解思維障礙 一輪復習追求深度學習
——2022年全國新高考Ⅰ卷第21題的深度思考

陜西 韓紅軍 趙偉華

2022年高考數學全國新高考Ⅰ卷立足《普通高中數學課程標準(2017年版2020年修訂)》，秉承了《中國高考評價體系》，考查數學關鍵能力、思維價值、核心素養的一貫設計理念，延續了以考查運算能力為主的傳統，堅持在平凡問題中考查真功夫、在主干知識中考查真能力.第21題貌似平和，實則在試題設置上，注重層次性，讓不同能力水平的學生都能夠得到充分的展示.

1 原題回放 霧里看花

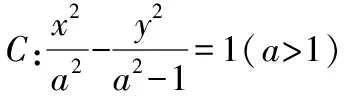
(1)求l的斜率；

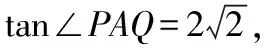
2 精彩多解 初始真容

此題打破經常考橢圓和拋物線的常規，以雙曲線為背景，重點考查雙曲線的標準方程，以及直線與雙曲線的位置關系，考查學生的數學運算能力、抽象概括能力和邏輯推理能力.此題題干簡單明了，不拖泥帶水，表面上看比較常規，實際上運算量和思維量較大.

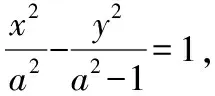
由題意顯然直線l的斜率存在，設l:y=kx+m，P(x1,y1),Q(x2,y2)，

聯立直線與雙曲線的方程得(2k2-1)x2+4kmx+2m2+2=0，

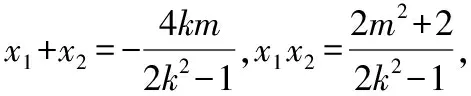
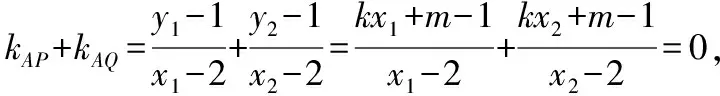
化簡得2kx1x2+(m-1-2k)(x1+x2)-4(m-1)=0，

即(k+1)(m+2k-1)=0，當m+(2k-1)=0時，直線l可化為y=kx-(2k-1)，即y-1=k(x-2)，直線l經過A點，不符合題意，舍去，故k+1=0，解得k=-1.所以直線l的斜率為-1.

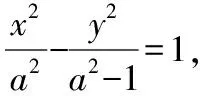
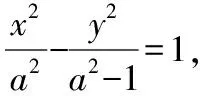
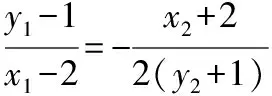
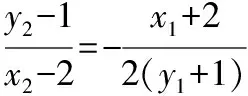
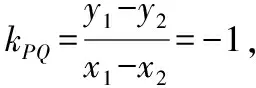
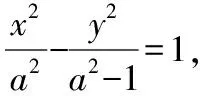
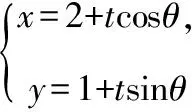
同理可得

(2)法一：設直線AP的傾斜角為α，

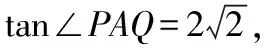
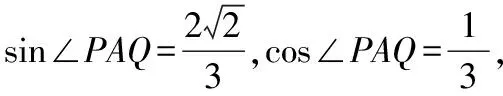
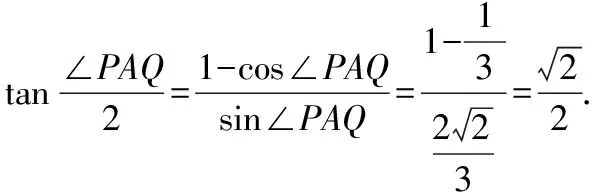
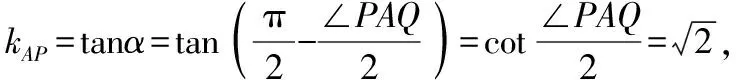
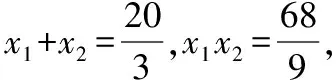
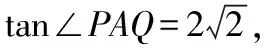
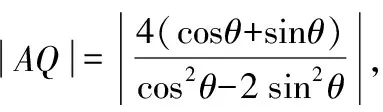
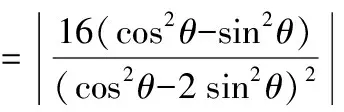
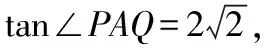
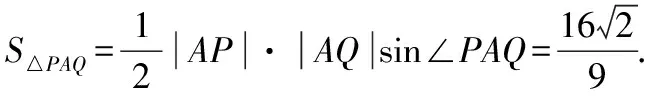
上述第(1)問分別從設直線AP的斜率k，設直線AP的參數方程，設直線l的斜截式方程，點差法等角度進行思考求解，第(2)問分別由tan∠PAQ求得kAP，將直線AP的參數方程代入雙曲線方程求得|AP|等角度出發，求得結果.具體可以由以下思維導圖展示.

第(1)問思維導圖：

第(2)問思維導圖：

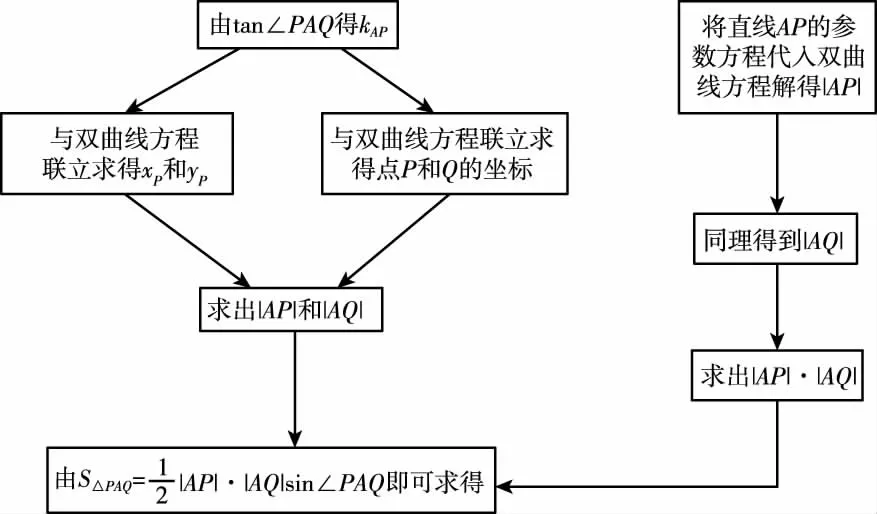
3 深度探究 觸摸本質

波利亞告訴我們：沒有任何一道題目是徹底完成了的，總還會有些事情可以做；在經過充分研究和洞察后，我們可以將任何解題方法進行改進，我們總可以深化對答案的理解.因此，我們在解題教學過程中，不能只停留在解出一道題的層面，要反思解題過程，善于抓住一閃而過的思維火花，深入挖掘解題過程中的規律性的東西，從變化中找出不變的東西，揭示規律，探尋本質.

3.1 深度探究 拓展推廣

此題的第(1)問能否一般化，其中又蘊含什么規律呢？于是我們得到如下命題.

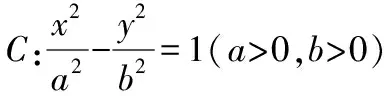
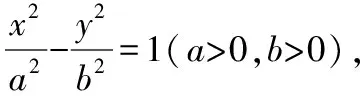
設直線PQ的方程:y=kx+m，P(x1,y1),Q(x2,y2)，聯立直線與雙曲線得(b2-a2k2)x2-2kma2x-a2m2-a2b2=0，

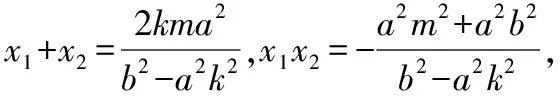
化簡得2kx1x2+(m-y0-kx0)(x1+x2)-2x0(m-y0)=0，

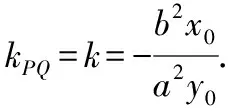
由于上述推理過程可逆，所以我們得到如下結論.

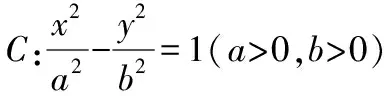
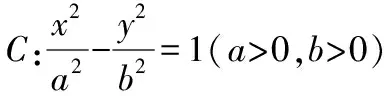
3.2 深度探究 類比推廣

如果將雙曲線換成橢圓或拋物線，經過探究，類似命題也成立，于是我們得到如下結論，證明過程與上述探究過程類似，留給有興趣的讀者.

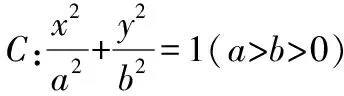
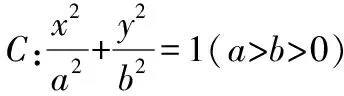
4 變式訓練 揭示規律

在對上述試題第(1)問的探究中，我們得到：如果兩條直線的傾斜角互補，那么這兩條直線的斜率之和為0.根據此結論我們可以解答如下一系列問題.

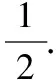
(1)求橢圓C的方程；

(2)若橢圓C的弦PA,PB所在直線交x軸于點C,D兩點,且PC=PD,求證：直線AB的斜率為定值.

【評注】對于此題第(2)問，因為PC=PD，易得PA,PB兩條直線的傾斜角互補，所以直線PA,PB的斜率和為0，所以可設直線PA的斜率為k，那么直線PB的斜率為-k，分別與橢圓方程聯立可得xA,xB，再利用斜率公式即可得到直線AB的斜率為定值.

(1)求橢圓的方程；

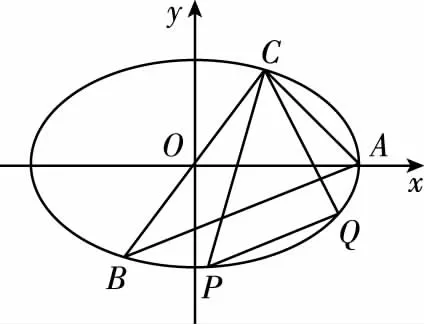
【評注】如圖，對于此題第(2)問，因為∠PCQ的平分線垂直于OA，易得PC,QC兩條直線的傾斜角互補，所以直線PC,QC的斜率和為0，所以可設直線PC的斜率為k，那么直線QC的斜率為-k，分別與橢圓方程聯立可得xP,xQ，再利用斜率公式即可得到直線PQ的斜率等于直線AB的斜率.

【變式3】如圖，已知橢圓的中心在原點，焦點在x軸上，長軸是短軸的2倍且經過點M(2,1)，平行于OM的直線l在y軸上的截距為m(m≠0),且交橢圓于A,B兩點.

(1)求橢圓的方程；

(2)求m的取值范圍；

(3)求證：直線MA,MB與x軸始終圍成一個等腰三角形.

【評注】對于此題第(3)問，設直線MA,MB的斜率分別為k1,k2，要證明直線MA,MB與x軸始終圍成一個等腰三角形，只需證明k1+k2=0即可.

上述三道題看似毫無關聯，但經過分析，我們發現，這三道題都用到了結論：如果兩條直線的傾斜角互補，那么這兩條直線的斜率之和為0.可見三道題存在著千絲萬縷的聯系，我們只有層層剝開迷霧，才可以領略到這三道題蘊藏的規律.

5 解后反思 啟示升華