數學運算視角下的原創試題命制
——一道命題征集活動試題命制過程與感悟

湖南 周志剛 譚宏志

數學是研究現實世界空間形式和數量關系的科學，而運算推理是重要的研究方法，數學運算在高中數學教學中具有重要價值，它在發展學生理性思維和培育學生思維能力中具有不可替代的作用.《普通高中數學課程標準(2017年版2020年修訂)》(以下簡稱《課程標準》)指出，數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的過程,主要包括：理解運算對象、掌握運算法則、探究運算方向、選擇運算方法、設計運算程序、求得運算結果.它是發現數學規律的重要工具,解決數學問題的基本手段,培養學生嚴格推理的重要途徑.數學運算是函數與導數板塊內容教學中應重點培養的核心素養之一,下面就筆者參與《教學考試》雜志社的命題征集活動中命制的一道函數與導數綜合題的命制歷程，與同行交流.

一、試題呈現與分析

【試題】已知函數f(x)=xlnx-(a+1)x+ea.

(1)當a>0時，求f(x)在(1,+∞)上的最小值；

(2)若不等式f(x)≤(x-a-2)ex-1+ea對x∈[1,+∞)恒成立，求a的取值范圍.

1.試題考查意圖

本題以函數為背景，以導數為工具，考查了函數與導數的綜合問題，具體考查利用導數研究函數的最值及不等式恒成立問題，考查了數學建模中的同構思想，考查運算求解能力、抽象概括能力及化歸與轉化思想，落實數學抽象、邏輯推理、數學運算等核心素養.

2.試題解法分析

第(1)問思路：通過求導，研究函數的極值，從而求出函數的最值；

第(2)問思路：不等式恒成立問題有兩種常規處理方法：(ⅰ)參變分離后轉化為求函數的最值；(ⅱ)構造相應的函數，通過對參數的分類討論，求出參數取值范圍，而本題第(2)問采用將兩邊式子轉化為相同結構后，利用同構思想轉化為研究函數的單調性，從而求出參數取值范圍.

解析：(1)依題意，f′(x)=lnx-a，令f′(x)=0，解得x=ea，因為a>0，所以ea>1，當1ea時，f′(x)>0，所以f(x)的最小值為f(ea)=ealnea-(a+1)ea+ea=0.

(2)解法一：由已知f(x)≤(x-a-2)ex-1+ea，

得xlnx-(a+1)x+ea≤(x-a-2)ex-1+ea

即xlnx-(a+1)x+ea≤(x-1)ex-1-(a+1)ex-1+ea=ex-1lnex-1-(a+1)ex-1+ea，

即f(x)≤f(ex-1)，因為ex-1≥x對一切實數恒成立，所以要使不等式f(x)≤f(ex-1)成立，

只需f(x)在[1,+∞)上單調遞增，又f′(x)=lnx-a，所以lnx-a≥0，即a≤lnx對x∈[1,+∞)恒成立，所以a≤(lnx)min=ln1=0，所以a≤0.

解法二：由已知f(x)≤(x-a-2)ex-1+ea，

得(x-a-2)ex-1-xlnx+(a+1)x≥0,

對x∈[1,+∞)恒成立，取x=e代入得，

令g(x)=(x-a-2)ex-1-xlnx+(a+1)x,x∈[1,+∞),g(1)=0.

g′(x)=(x-a-1)ex-1-lnx+a,顯然g′(1)=0，

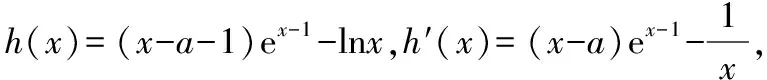
h′(x)單調遞增，令h′(1)≥0，解得a≤0，

當a≤0時，對x∈[1,+∞)，h′(x)≥h′(1)≥0，于是h(x)在[1,+∞)上單調遞增，

又h(x)≥h(1)=0，所以g(x)在[1,+∞)上單調遞增，所以g(x)≥g(0)=0，

即(x-a-2)ex-1-xlnx+(a+1)x≥0.

當a>0時，存在x0∈(1,+∞)使得h′(x0)=0，

因為當1x0時，h′(x)>0，所以h(x)有最小值h(x0)，且h(x0)

綜上,a的取值范圍為(-∞,0].

二、試題命制立意

1.明確考查知識

根據預先制定的雙向細目標，明確了考查的必備知識為函數與導數及其應用，具體考查的內容是利用導數研究函數單調性與極值(或最值)，并據此解決函數與方程和不等式有關的問題.

2.預設度量難度

根據命題構想，本題作為考試試卷的第20題，難度系數控制在0.35，具有一定的區分度，屬于試卷中等偏難題.

3.明確考查能力

本題主要考查運算求解能力、抽象概括能力以及在處理數學對象時構建數學模型的能力.

4.明確考查思想

在解決函數與導數問題中，函數與方程、分類討論、化歸與轉化、數形結合思想往往會同時體現，本題在命制中明確將構建數學模型的同構思想作為考查的重點，著重考查函數與方程，化歸與轉化思想.

三、試題命制歷程

1.試題背景

本題的試題素材來自于廈門大學研究生入學考試題：

ey+xlnx-x-xy≥0(x≥1,y≥0).

2.試題加工與完善

原題是雙變量構成的二元不等式，筆者以該二元不等式左邊為目標，預設變量x為主元，y為參數，于是得到原型函數f(x)=xlnx-(a+1)x+ea，再結合命題立意的要求，形成了第一稿：

已知函數f(x)=xlnx-(a+1)x+ea(a>0).

(1)求f(x)在(1,+∞)上的最小值；

(2)若不等式f(x)≤(x-a)ex-1+ea對x∈[e,+∞)恒成立，求a的取值范圍.

但是在筆者解析過程中發現第二問由不等式求參數取值范圍時，不利于下一步的計算，于是對函數進行調整，并形成了第二稿：

已知函數f(x)=xlnx-(a+1)x+ea(a>0).

(1)求f(x)在(1,+∞)上的最小值；

(2)若不等式f(x)≤(x-a-2)ex-1+ea對x∈[e,+∞)恒成立，求a的取值范圍.

調整后第二問的解析：

由已知f(x)≤(x-a-2)ex-1+ea，

得xlnx-(a+1)x+ea≤(x-a-2)ex-1+ea

即xlnx-(a+1)x+ea≤(x-1)ex-1-(a+1)ex-1+ea=ex-1lnex-1-(a+1)ex-1+ea，

即f(x)≤f(ex-1)，因為ex-1≥x對一切實數恒成立，所以要使不等式f(x)≤f(ex-1)恒成立，

只需f(x)在[e,+∞)上單調遞增，又f′(x)=lnx-a，所以lnx-a≥0，即a≤lnx對x∈[e,+∞)恒成立，

所以a≤(lnx)min=lne=1，所以0

考慮其中ex-1≥x對一切實數恒成立.但是當x=e時等號不成立，學生解題方法會因此受限，于是筆者進一步修改自變量的范圍形成了第三稿：

已知函數f(x)=xlnx-(a+1)x+ea.

(1)當a>0時，求f(x)在(1,+∞)上的最小值；

(2)若不等式f(x)≤(x-a-2)ex-1+ea對x∈[1,+∞)恒成立，求a的取值范圍.

這也是最終形成的定稿.

四、命題感悟

1.試題亮點

回顧試題命制過程，注重知識與方法，能力與素養的并重，體現了新高考命題的方向，主要有以下幾個亮點：(1)素材選擇來源于研究生考試試題，體現高考為大學選拔人才的功能，經過深加工后的函數模型是對數型函數，貼近高考，學生易于接受；(2)重視數學運算核心素養的考查，試題第(1)問屬于常規考查，難度適中，大部分學生均可順利完成，第(2)問通過改變參數與取值范圍，讓學生可從不同角度與方法解決，淡化技巧，注重通性通法，注重對主干知識的考試，突出數學本質；(3)注重數學思想的考查，本題考查的函數與方程、化歸與轉化思想均為高中數學重要的數學思想，基于構建數學模型的同構思想是最大亮點；(4)命題中筆者嚴格遵循《課程標準》中的高考命題建議，同時兼顧當前學校學生的學情，試題有梯度，有人文關懷.

2.命題感悟

通過本次原創試題命制，筆者有以下幾點感悟：

(1)遵循標準，體現精神

命題是為選拔人才服務，所命試題要符合《課程標準》要求，體現高中數學的育人導向，培育科學精神和創新意識.

(2)精選素材，體現功能

命題要精選素材，好的素材是命制好試題的基礎，教師應該在平時廣泛閱讀，留心積累，認真研究教材與高考真題，對于競賽題和大學試題也可嘗試了解研究，選好素材后，在命制過程中要體現考試的核心功能，堅持素養導向，能力為重的原則.

(3)兼顧學情，體現素養