研究高考真題 提升核心素養
——以一道“爪型”三角形的變式探究為例

四川 鄧成兵

“爪型”三角形是指在給定的一個三角形中，連接一個頂點和對邊上的任意一點構成的圖形.“爪型”三角形問題主要考查直觀想象、數學運算、數據分析、邏輯推理等數學核心素養.筆者就從“爪型”三角形的代數特征和幾何特征出發，力求在解法上尋求最簡潔的方法，總結解題規律，從整體上認識把握，做到有的放矢.

《普通高中數學課程標準(2017版2020年修訂)》中指出，高中數學教學應該以發展學生數學核心素養為導向，創設合適的教學情境，啟發學生思考，引導學生把握數學內容的本質，達到學生用科學方法分析問題、解決問題，才有利于引導學生將其轉化為自己的思維方式.高考真題承載著引領教學的功能，作為重要的教學素材，試題的價值一直被教師在教學中深入思考、充分挖掘，變式探究、類比深化，全方位探究高考題的相關性及同源性.

從2015年到2022年，全國每年高考均出現“爪型”三角形，其中以解答題形式出現理科5次、文科4次，填空題文理科均為5次，選擇題文理科均出現1次(如下統計表所示).本文以2022·全國甲卷·16的探究、發現過程中，從解法探究，到變式推廣，再到獲得“爪型”三角形相關性質.整個過程可以說是順應了提升學生的數學核心素養.現與大家分享、交流.

“爪型”三角形在近八年高考中的地位及難度分析

1.試題呈現與解法探究

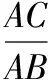
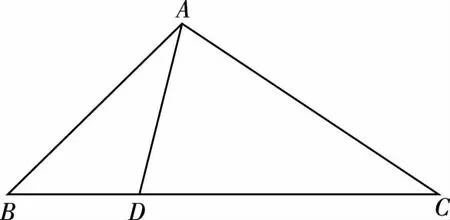
【命題意圖】本題是典型的“爪型”三角形問題，需要靈活應用正、余弦定理進行邊角互化與基本不等式求解；從多維度多方面考查學生的數學運算、數據分析、邏輯推理、直觀想象等數學核心素養，綜合性較強.

【解法一】(利用兩次余弦定理列方程求解，即代數法)

設BD=x，CD=2x，△ABC中，角A,B,C所對的邊分別為a,b,c,

在△ACD中，b2=4x2+4-2·2x·2·cos60°，

可得,b2=4x2-4x+4，

在△ABD中，c2=x2+4-2·x·2·cos120°，

可得，c2=x2+2x+4，

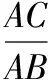
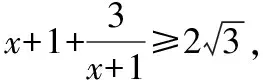
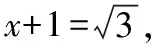
【解法二】(利用平面向量坐標法求解，即幾何法)

以D為坐標原點建立如圖所示平面直角坐標系，

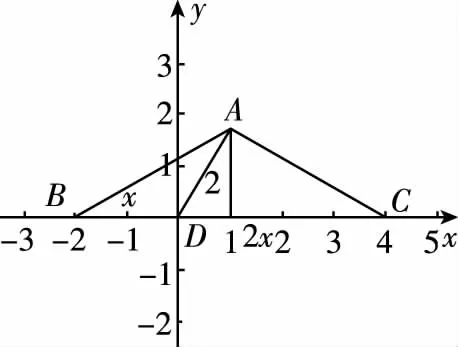
設BD=x(x>0)，

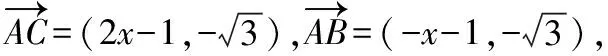
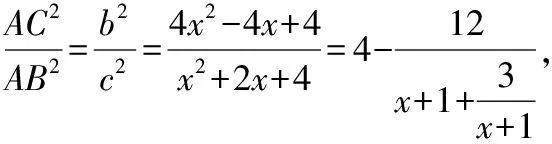
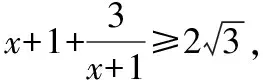
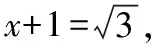
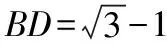
【解法三】(利用等面積法求解，即代數法)

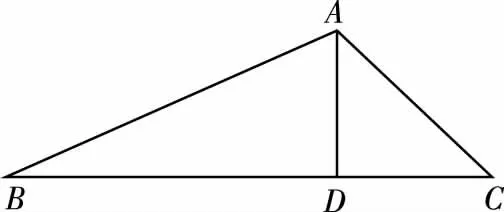
設BD=x，CD=2x，如圖，過頂點A作AE⊥BC于點E，

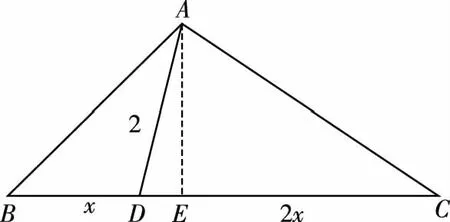
∵S△ABC=S△ABD+S△ACD，

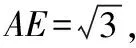
則BE=x+1,CE=2x-1，

在Rt△ACE中，AC2=CE2+AE2=(2x-1)2+3=4x2-4x+4，

在Rt△ABE中，AB2=BE2+AE2=(x+1)2+3=x2+2x+4，

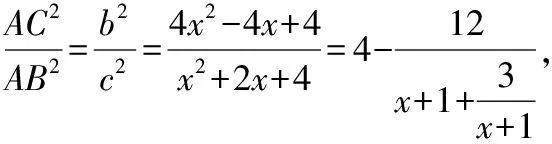
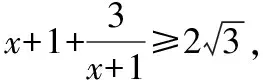
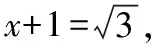
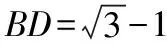
評析：解法一先算“兩次”策略，依據余弦定理列方程求解，即代數方法，得到AC,AB兩邊關于x的關系式，再利用基本不等式進行求解；解法二建立直角坐標系，運用向量的模長公式得到AC,AB兩邊關于x的關系式，再運用基本不等式進行求解；解法三利用三角形的等面積法，得到AE的長度，結合直角三角形，利用勾股定理并結合基本不等式進行求解.解法三相對解法一和解法二，運算比較小，降低了運算量，在教學中，應該重視正余弦定理列方程組法、平面向量坐標法及等面積法在“爪型”三角形中的應用.

【解題思維導圖】

解法一：

解法二：

解法三：

2.變式探究

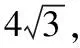
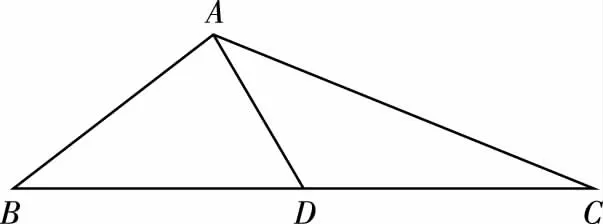
【解法一】(算“兩次”策略，依據正余弦定理列方程求解，即代數方法)

設BD=CD=m，AD=n，

在△ABD中，由余弦定理得c2=n2+m2-2×mn·cos∠ADB.①

在△ACD中，由余弦定理得

b2=n2+m2-2×mncos∠ADC.②

∵∠ADB+∠ADC=π，

∴cos∠ADB+cos∠ADC=0，

所以①+②，得b2+c2=2n2+2m2， ③

在△ABC中，由余弦定理得

4m2=b2+c2-2bccos∠BAC，

又∠BAC=120°，所以4m2=b2+c2+bc， ④

聯立③④得，2b2+2c2-4n2=b2+c2+bc，

即b2+c2=bc+4n2≥2bc，

即bc≤4n2，當且僅當b=c=2n時，等號成立.

即AD=2.

【解法二】(用基底法對向量進行分解后平方轉化為模長和數量積問題探究b,c間關系，即利用向量或坐標方法求解)

設AD=n,

∵D為BC的中點，

即b2+c2=bc+4n2，

而b2+c2≥2bc，

∴bc+4n2≥2bc即bc≤4n2，當且僅當b=c=2n時，等號成立，

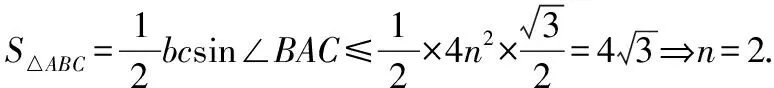
即AD=2.

探究一類問題，形成結論

思考：把變式1中解法一③式中的m,n分別換成BD，AD，你會獲得什么結論？

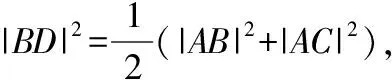
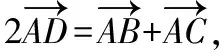
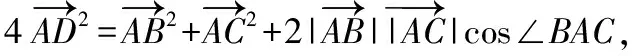
由①+②化簡得，

∵D為BC的中點,

∴|BC|=2|BD|,代入③化簡得,

【解法三】(結論應用)

設BD=CD=m，AD=n，

在△ABC中，利用余弦定理可得，

4m2=b2+c2-2bccos120°，化簡得，

把②代入①化簡得，

4n2+bc=b2+c2，

而b2+c2≥2bc，

∴bc+4n2≥2bc即bc≤4n2，

當且僅當b=c=2n時，等號成立，

即AD=2.

評析：解法一利用兩次余弦定理，互為補角的兩余弦值為零及基本不等式求解，難度較大，運算也比較大；解法二利用平面向量的中線公式，再運用基本不等式求解，運算較小,但難度較大；解法三與解法一和解法二比較，更加簡便、高效，難度較小.本類題型側重三角形的正余弦定理、誘導公式、三角形的面積公式、平面向量的中線公式及基本不等式，考查數形結合與化歸轉化思想，數學運算、邏輯推理等核心素養.

變式2：記△ABC的內角A,B,C的對邊分別為a,b,c.若AD為∠BAC的平分線，交BC邊于D點，AD=2,∠BAC=120°,求b+c的最小值.

【解法一】(等面積法求解，即代數方法)

由題意得，作出圖象，如圖所示.

設∠BAD=∠CAD=60°,∠BAC=120°，

∵S△ABC=S△ABD+S△ACD,

∵|AD|=2,

當且僅當b=c時,等號成立,

∴b+c的最小值為8.

探究一類問題，形成結論

結論2.由(*)化簡得“爪型”三角形的角平分線公式：在△ABC中,∠BAC的平分線AD與BC邊相交于點D，設∠BAD=∠CAD=θ,則∠BAC=2θ，則角平分線長度|AD|=

【解法二】(結論應用)

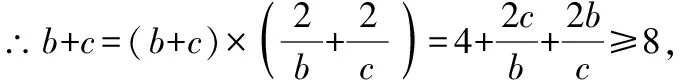
∴b+c的最小值為8.

評析：角平分線型側重正余弦定理、三角形面積公式、兩角和差的三角公式、二倍角公式、三角函數的性質以及角平分線定理的應用.解法一運用了三角形的等面積法及基本不等式的乘“1”法求解，學生難以想到，難度較大；解法二直接運用“爪型”三角形的角平分線公式及基本不等式的乘“1”法求解，難度較小，學生容易想到，考查邏輯推理能力、直觀想象、數學運算、數學建模等核心素養.

思考：若點D不是角平分線與BC邊的交點，為BC邊上任意一點，也有相似的結論嗎？

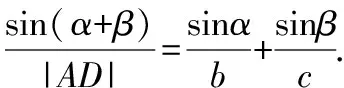
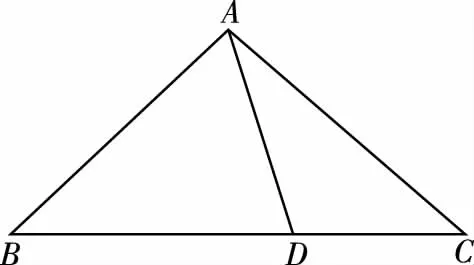
【分析】在三角形中出現了邊和角的正弦，運用S△ABC=S△ABD+S△ACD，利用三角形面積的第二公式得證.

證明：∵S△ABC=S△ABD+S△ACD,

sinβ,

兩邊同時除以bc×|AD|,化簡得,

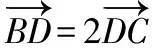
【解題思路】(用向量或坐標方法求解)

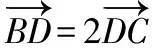
∵|AD|=2，∠BAC=120°,

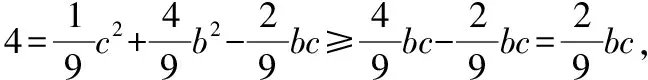
解得bc≤18，

評析：由此解法中的(*)可得一般情況下爪型三角形的向量表示.

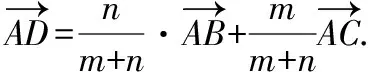
證明：∵|BD|=m,|DC|=n,

變式4：記△ABC的內角A,B,C的對邊分別為a,b,c.若AD⊥BC，交BC邊于D點,∠BAC=120°，AD=2,S△ABC的最小值為.

【解題思路】(等面積法和余弦定理求解)

在△ABC中，a2=b2+c2-2bc×cos120°,

∴bc≥16,

評析：該類題目側重直角三角形中互余兩角的三角函數關系及兩角和差的三角公式的應用.考查數學運算、數據分析、直觀想象等核心素養.

每年高考真題都有源自于教材的例習題改編或組合，重在考查學生的基本知識、基本思想和基本技能，對學生的思維量、靈活性、數學核心素養提出較高要求.本題源于人教A版必修四第147頁A組第13題改編，如變式5.

變式5：如圖所示，l1,l2,l3是同一平面內的三條平行直線，l1與l2間的距離是1，l2與l3間的距離是2，正三角形ABC的三頂點分別在l1，l2，l3上，則△ABC的邊長是________.

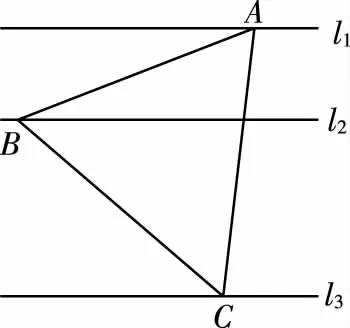
【解題思路】(正弦定理和三角形兩角和與差公式求解)

設AC與l2交于D,設∠BDA=θ，∠DBA=β，設正三角形ABC的邊長為a，

兩式相除化簡得，2sinβ=sin(60°-β),

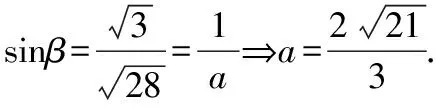
評析：該類題目側重三角形面積公式、兩角和與差公式、二倍角公式、正余弦定理及其應用，考查邏輯推理、直觀想象、數學運算等核心素養.

3.方法反思和素養展現

文章以2022年全國甲卷文理科第16題及變式,用不同的方法對“爪型”三角形進行了深入探究，歸納出“爪型”三角形的中線、角平分線、高線常規解法及相關二手結論并對其證明；運用了特殊到一般的數學思想、化歸與轉化思想、函數與方程等思想；“爪型”三角形在高考試卷中屬于難度中等，解這類三角形方法很多，通常可以采用“鄰補角策略”“算兩次”策略依據正余弦定理列方程求解；也可以采用作高、作平行線等手段利用初等幾何知識求解；亦可借助向量工具采用基底法對向量進行求解.但如果運用本文總結的爪型三角形的四條性質求解，不但可以簡化我們的運算，還可以提高做題的速度及正確率.