真題引領 多維變式 促進高效備考
——基本不等式變式復習探究
2022-11-30 10:21:16廣東朱國增雷雄軍
教學考試(高考數學) 2022年6期
廣東 朱國增 雷雄軍
基本不等式是不等式中的重要內容,新教材中將基本不等式放在第一冊的第二章,函數的概念和性質章節的前面,很大一部分原因是基本不等式是研究函數值域、求函數最大值或最小值、求參數取值范圍的常用工具.其應用范圍涉及高中數學的很多章節,如涉及函數、解三角形、數列、解析幾何等有關取值范圍、最值的考查.因此高考中很少單獨考查基本不等式,都是與其他知識融合考查.2022年全國新高考Ⅰ卷對基本不等式的考查是第17題與解三角形的知識融合.2022年全國甲卷理科對基本不等式的考查出現了兩處,一處是第16題與解三角形的知識融合,另外一處是第20題與圓錐曲線的知識融合.2022年全國乙卷理科對基本不等式的考查也出現了兩處,一處是第9題與立體幾何的知識融合,另外一處是第23題的不等式選講題目中.雖然基本不等式的內容不是很多,但是其內容具有變通靈活性、應用廣泛性,因此常常受到命題者的青睞,且常考常新.筆者從真題考查方向入手研究,將基本不等式的知識進行了多維的變式,在變式拓展中揭示了基本不等式的內涵和價值,提高學生解題時的應變能力,進而促進高效備考.
一、母題的選取及分析
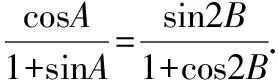
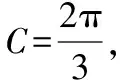
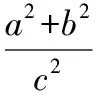
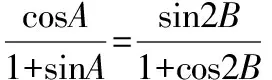
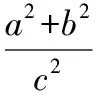
二、知識變式深化學生對知識的理解


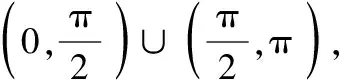

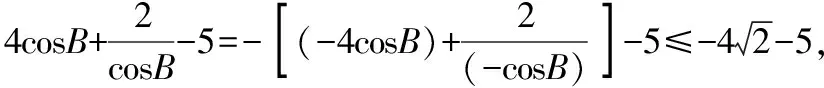
因此我們可以和學生總結如果形式滿足但值不為正則變號處理.

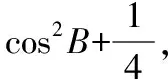
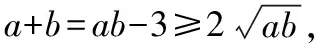


以上從知識的維度對常見基本不等式求最值的情形進行了多角度的變式,通過變式深化了學生對基本不等式知識的理解.避免常見的基本不等式使用誤區.
三、方法變式拓寬學生的解題思路
基本不等式的考查中有一種常見題型就是1的代換,巧妙利用1的代換將要求的最值問題轉化為基本不等式求解.如下題:

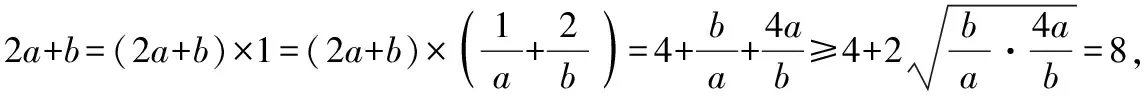

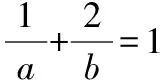
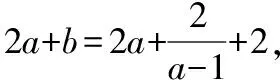
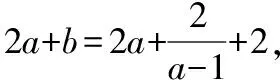
對于一個數學問題,因思考的角度不同,可得到多種不同的思路,使得學生的思維不會被題型所局限.解題時候,啟發學生從不同角度進行思考,拓寬學生的解題思路.
四、綜合變式提高學生的應變能力

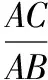
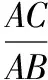

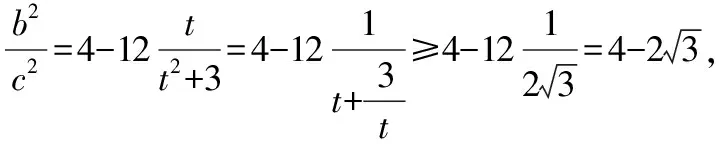




猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
今日農業(2021年19期)2022-01-12 06:16:36
中老年保健(2021年11期)2021-08-22 03:15:44
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學生數理化(高中版.高考數學)(2021年1期)2021-03-19 08:28:38
現代出版(2020年3期)2020-06-20 07:10:34
作文世界(小學版)(2018年4期)2018-10-16 17:13:34
快樂作文·低年級(2016年12期)2017-01-03 20:52:44
快樂作文·低年級(2016年6期)2016-06-24 18:58:40

