基于WIM的大跨鋼箱梁懸索橋疲勞荷載譜研究

賀偉誠，王 超

(湖北工業大學土木建筑與環境學院，湖北 武漢 430068)

大跨度橋梁主梁廣泛采用正交異性鋼橋面板鋼箱梁結構，這種結構具有自重輕、抗扭及橫向抗彎剛度大、整體性強、經濟性好等優點[1]。然而，由于車輪荷載的反復作用，加之焊接殘余應力及初始缺陷的影響，橋梁極易產生疲勞損傷累積，嚴重時甚至造成結構破壞。針對鋼箱梁疲勞損傷問題，研究建立疲勞車輛模型并分析各車型對橋梁疲勞損傷貢獻率是重要的方向之一，國內外學者在該領域開展了相關的研究工作。宗周紅等[2]研究了京滬高速公路的重車疲勞荷載譜，發現重車占比較高，且六軸二類車型為等效標準疲勞車。胡森林等[3]提出了針對廣西地區疲勞設計的疲勞損傷修正系數建議值。王元清等[4]針對建立的車輛荷載模型進行分析，得出42 d樣本量可以用來代表整體分布特征的結論。鄧揚等[5]、Zhang等[6]研究了分時段的疲勞荷載譜，前者發現晚上超車道的車重均值比白天高，后者發現汀九橋的疲勞壽命在120 a的設計限值內。Yan等[7]研究了中、小跨徑橋梁的疲勞應力譜，發現超載控制對于疲勞應力譜中高幅應力的概率密度有很大的影響。翟慕賽等[8]建立了不同等級公路的疲勞荷載譜，發現不同等級公路其疲勞荷載模型也不同。孫秀雅等[9]基于疲勞荷載譜針對壩陵河大橋疲勞易損部位進行了疲勞壽命分析，得出橋上疲勞細節的疲勞壽命高于設計值的結論。陳斌等[10]研究了目標基準期內車輛荷載的極值分布，發現車輛荷載存在離散性大的特點。羅媛等[11]提出了橋梁上基于隨機重載車流的疲勞可靠度分析方法，發現車輛軸數多少和橋梁等效疲勞應力幅的高低存在負相關性。劉揚等[12]研究了關于隨機車流作用下簡支梁橋設計基準期內荷載效應極值概率分布的問題。Deng等[13]建立了疲勞荷載譜并單獨討論了六軸車的車輛模型，提出了一種針對疲勞車輛模型研究的新方法。MulyadiEndang等[14]進行了對比S-N曲線與標稱疲勞抗力的研究，得出S-N曲線上50 a壽命依然低于疲勞極限的結論。Guo等[15]利用車輛疲勞荷載譜對橋梁的可靠度進行了分析，發現隨著時間的推移和車流量增加，可靠度會加速降低。

我國幅員遼闊，各地環境不同、橋型各異、交通流量狀況復雜多變，對于不同地區橋梁特別是特大跨度鋼箱梁橋的疲勞問題，有必要針對其實際運營環境進行專門的研究分析[16]。另外，橋梁的實際交通狀況會受工作日、節假日、季節變化影響發生改變，為了確保統計得到的疲勞荷載譜更加準確和具有代表性，有必要采用較長時間段的數據進行分析。因此，本文將針對某大跨度正交異性橋面板鋼箱梁懸索橋進行疲勞分析，利用動態稱重系統(WIM)長期采集的實橋車輛荷載數據進行統計分析，引入確定模型最佳分量數的兩種準則，采用混合高斯分布擬合車重數據的分布規律，得到車重概率密度曲線并建立疲勞荷載譜，進而計算出各車型對該橋的疲勞損傷貢獻率。

1 車輛荷載數據統計

1.1 工程概況

某大跨度鋼箱梁懸索橋是繞城公路的重要組成部分，設計速度為120 km/h，鋼箱梁主梁全寬38.5 m，設雙向六車道，主梁橫斷面布置圖如圖1所示。為了保障大橋的安全運營，大橋建設了橋梁健康監測系統，實時采集包括車輛信息在內的各類橋梁運營期的關鍵參數。由于此橋地處城市外環，是連接市內外的樞紐，交通量大，車型多樣，交通狀況復雜，不同車型會對橋梁造成不同程度的疲勞損傷，因此，這里將對該橋WIM系統采集的長期車輛荷載數據進行分析研究。

圖1 某鋼箱梁懸索橋橫斷面圖 mm

1.2 車型分類

由于實際車輛類型龐雜，沒有必要對每一種車型進行統計分析，為了分析簡易性和有效性，需要對其進行分類。由于結構疲勞損傷主要由應力幅和循環次數控制，而正交異性橋面板鋼箱梁應力幅循環次數主要受軸數影響，這里依據軸數將車輛進行分類，特別是實際交通流中大量存在的各種兩軸車都歸為一類。另外，車輛荷載與橋梁疲勞壽命成負相關性，過小的車輛荷載對疲勞壽命的影響可忽略不計，為了簡化分析，可以先對數據進行預處理，剔除車重過小(小于3 t)的車輛[17]，再進行統計分析，預處理后得到的各典型車型交通量如表1所示。

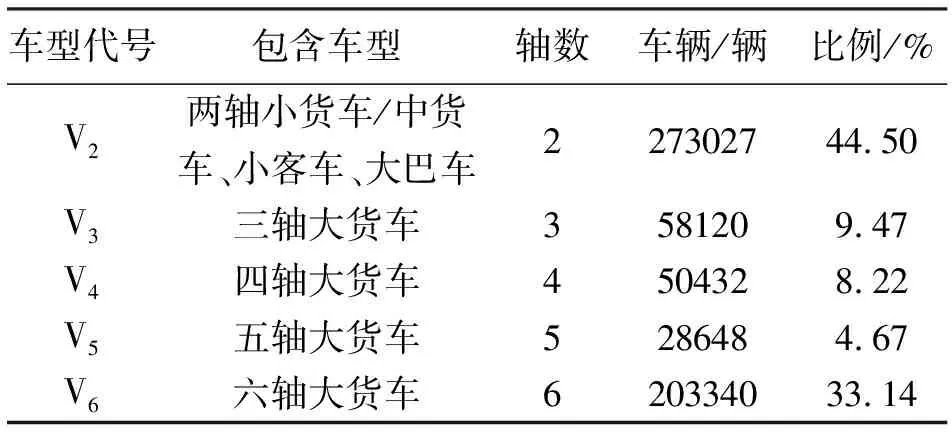
表1 各典型車型交通量

從統計結果可以看出該橋車流量以V2型車即兩軸車為主，占到了44.5%，六軸大貨車僅次于兩軸車，相對占比也比較高，達到33.14%，其他四種車型占比均低于10%。考慮到相對于其他大貨車來說，兩軸車載重和軸數相對較小，多軸大貨車的疲勞影響也不容小視，下文將對此進行詳細分析。

1.3 交通量統計

基于表1的典型車輛分類，現統計出每周各車型的車流量情況，由于少部分數據缺失，故共分析了24周的車輛數據，統計的各車型車流量變化如圖2所示。從圖2a可知各周的車流量變化都比較明顯，其中第22周的變化尤為顯著，推測可能是橋面檢測或維修等原因導致；從圖2b可以直觀看出各周車流量的構成也存在不同程度的變化，兩軸車和六軸車占比變化更為突出，并且兩類車占比趨勢基本相反。

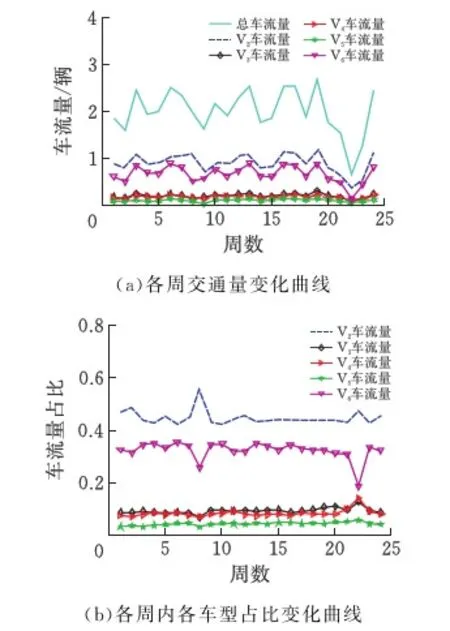
圖2 交通量變化

由于不同車型及車重的車流量每周變化明顯，需要采用較長時間的監測數據統計分析車流荷載分布特征，才能減少因偶然性而導致數據出現過大或過小的情況發生，從而確保建立的疲勞荷載譜更加準確并且具有代表性。

2 模型車輛疲勞荷載譜

2.1 車重統計

基于表1的交通量統計，再依據各類型車車重數據即可統計得到各車型的車重分布特征。以V2車型為例，根據實測數據統計其車重分布如圖3所示。這里將根據車重分布圖擬合其概率密度曲線，由圖3可以看出，車重分布圖呈現出多峰的形式，普通正態分布(圖中虛線)很難較好地擬合其分布特征，擬采用混合高斯分布擬合該分布規律，其概率密度函數如式(1)：

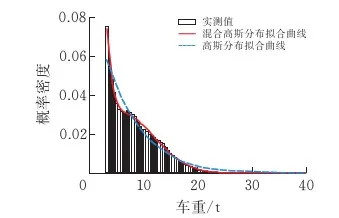
圖3 二軸車的車重-概率密度及擬合曲線

(1)

式中：M為分量數，描述分布峰值個數；Pi為各分布型對應的系數；fi(x)為各高斯分布的概率密度函數。

采用混合高斯分布擬合需要確定擬合曲線的高斯分量數，當分量數過小時，其擬合效果較差，分量數過多又會使問題變復雜，對于解決實際工程問題收效不大。為了更加準確描述概率分布情況，這里引入赤池信息準則(AIC)和貝葉斯信息準則(BIC)來優化確定最佳分量數，AIC和BIC分別定義為式(2)和(3)：

AIC=-2lnL+2M

(2)

BIC=-2lnL+MlnN

(3)

(4)

式中：M為分量數；lnL為模型的對數極大似然函數值；N為模型中數據的個數；SSE為殘差平方和，具體見式(5)。

模型最佳分量數的選取應優先考慮AIC值，取AIC最小時對應的M值；而當AIC值相差不大時，則引入BIC，最優分量數依舊取其值最小時對應的M值。

對于概率密度函數擬合的效果，采用擬合函數的SSE(和方差)以及R2(確定系數)進行評估，其定義為：

(5)

(6)

擬合曲線的和方差值越接近0，確定系數越接近1，則擬合效果越好。

針對圖3所示的V2型車，計算出采用不同分量數的混合高斯分布擬合車重概率分布時對應的AIC和BIC值，如圖4所示。

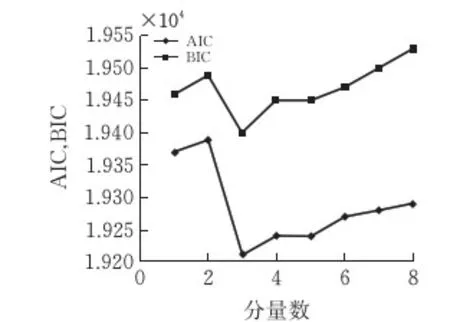
圖4 V2型車混合分布模型信息準則值變化曲線

由圖可見，當分量數為3時，AIC和BIC的值均達到最小，故V2型車多峰分布模型的分量數M取3。相應的混合高斯分布擬合曲線如圖3中紅線所示。

為了檢驗實測值的統計規律和擬合曲線之間的契合度，可求解出擬合函數的SSE(和方差)以及R2(確定系數)，其擬合優度如表2所示。

從統計結果可以看出，V2型車數量最多，車型復雜，但整體而言車重量都不大，基本在6～13 t之間。采用同樣的方法，對其他四種車型的車重進行統計，具體統計結果如圖5所示，可以發現三軸車和四軸車的車重分別為10.64 t和14.55 t時概率密度均達到最大峰值，且三軸車和四軸車分布規律類似，均出現峰與峰之間距離過大的情況，最右的一個峰其峰值較低，此峰值表明存在部分車輛滿載或超載；五軸車和六軸車均呈現為雙峰，兩類車型的車重分別為16.39 t和17.98 t時概率密度達到最大峰值。而用于擬合各車型車重概率分布的分量數、擬合曲線的參數以及擬合優度等參數可見表2。

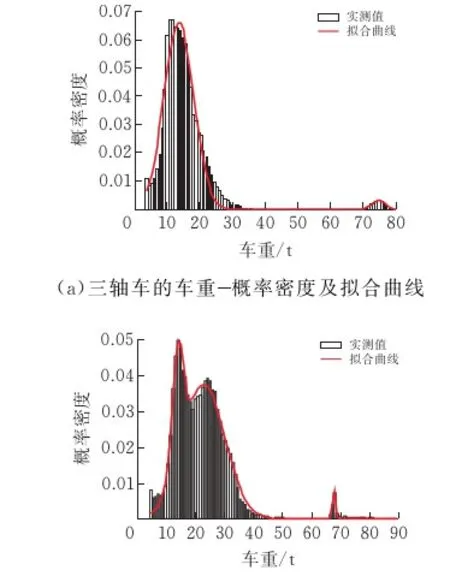
圖5 各車型車重概率密度模型

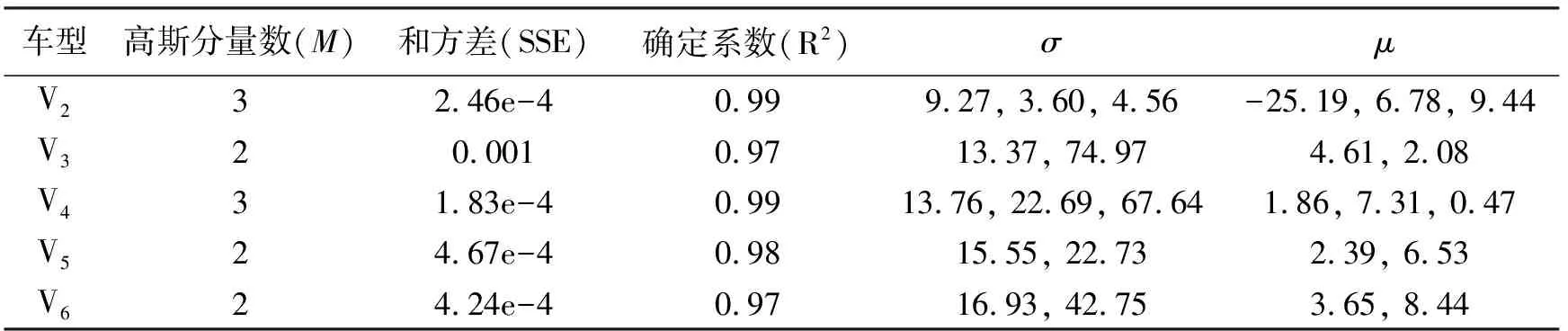
表2 各類車型車重概率密度曲線擬合參數及擬合優度

由表2各車型概率密度擬合曲線的和方差以及確定系數可知，五種車型混合高斯分布的和方差均接近于0，確定系數均大于0.96，由此可以確定混合高斯分布能較好擬合各車型的概率密度曲線。

2.2 建立疲勞荷載譜

依據Miner線性積傷率和等效疲勞損傷原理，當累計疲勞損傷相同時，可以將i個不同車重作用1次視為1個等效車重作用i次，等效車重計算式如下：

(7)

式中：W(eq)k為第k種車型的等效車重；pi為第k種車型中i車出現的頻率；Wi為該車車重。

將原始數據中每種車型的各軸重分別統計，計算各軸重在車重的占比，即可得到各車型軸重分配系數γk，計算方法如式(8)所示，表3為各車型軸重分配系數。

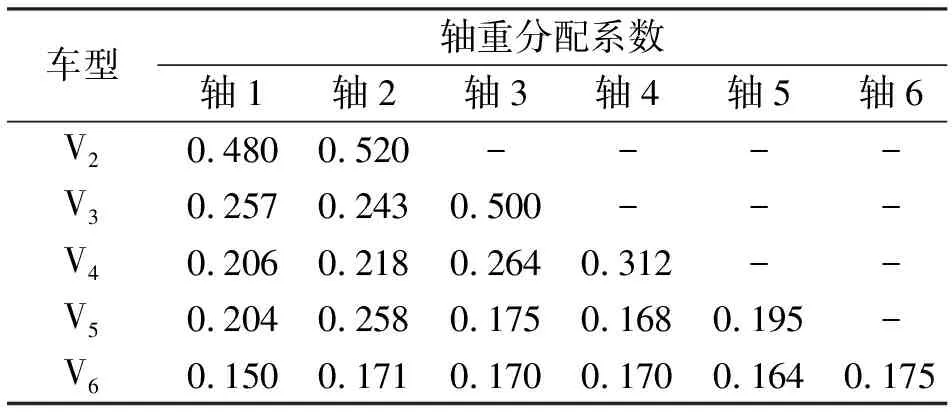
表3 各車型軸重分配系數

(8)

式中：γk為第k種車型的軸重分配系數；ω(eq)k,j為第k種車型第j軸的等效軸重；W(eq)k為第k種車型的等效車重。

運用式(7)計算出等效車重后，再結合軸重分配系數即可得到各車型的等效軸重數據，然后建立車輛的疲勞荷載譜，見表4。

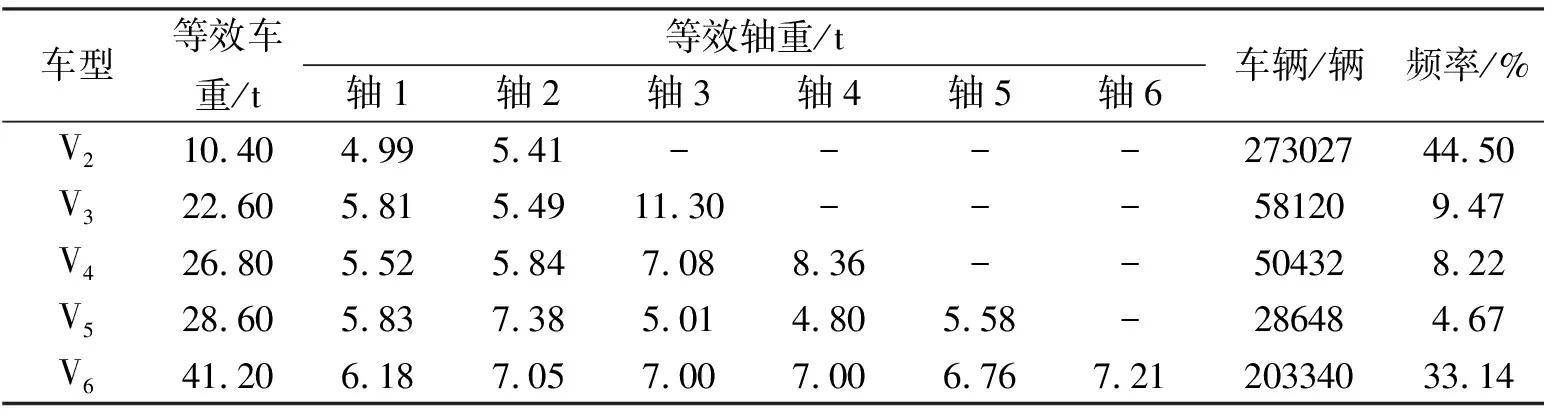
表4 疲勞荷載譜

3 疲勞損傷貢獻率

橋梁結構的疲勞損傷性能可以由不同車輛對橋梁產生的疲勞損傷貢獻率來反映，各車型對結構產生的損傷值和疲勞損傷貢獻率根據上文統計的車輛疲勞荷載譜來計算。對于正交異性橋面板鋼箱梁，橋面板鋼結構在車輛局部荷載作用下應力影響線很短[18]，局部效應比較明顯，所以結構疲勞損傷與軸重直接相關，可以通過計算等效軸重的疲勞貢獻率再結合軸數來得到等效車重的疲勞貢獻率。具體計算方法如下：

第k種車型第j軸等效軸重造成的橋梁損傷值D(eq)k,j為：

(9)

式中，c為結構或材料的性能參數；β為軸重引起的應力幅值系數；m為S-N曲線的斜率負倒數，取m=3；nk,j為第k種車型第j軸的總軸數；ω(eq)k,j為第k種車型第j軸的等效軸重。

各軸產生的總疲勞損傷值D為：

(10)

式中，kmax為車型總數；jmax為第k種車型的最大軸數。

第k種車型第j軸等效軸重造成的疲勞損傷貢獻率為：

(11)

第k種車型的疲勞損傷貢獻率λk定義為：

(12)

由此可以計算得到各軸及各車型對橋梁造成的疲勞損傷貢獻率，如表5所示。

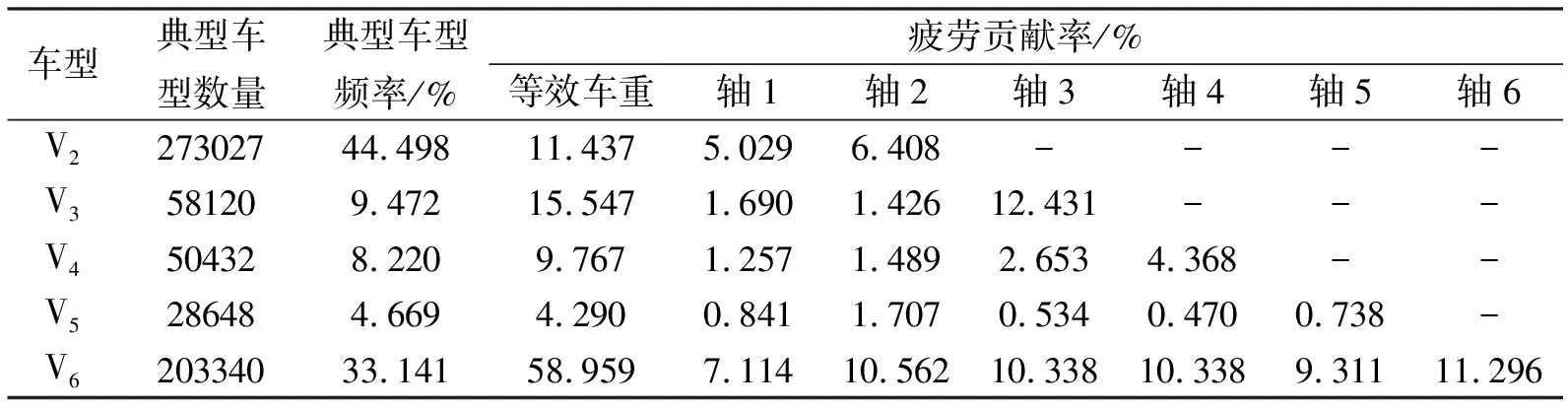
表5 各軸及各車型的疲勞貢獻率

從表5數據可以看出：1)兩軸車的頻率在各類型車中最大，但六軸車等效車重和各軸等效軸重產生的疲勞貢獻率最高，原因是在疲勞損傷貢獻率的計算中等效軸重的權重高于車輛數，并且六軸車的軸數最多、該車型各軸等效軸重相比于其它車型也較高；2)兩軸車頻率遠遠高于三軸車，但等效車重產生的疲勞損傷貢獻率卻略低于三軸車，原因是雖然這兩類車型的軸1和軸2等效軸重相差不大，但三軸車的第3軸的等效軸重遠高于兩軸車的所有軸重；3)四軸車和五軸車的頻率本身較低，并且各軸等效軸重都不高，最終產生的疲勞損傷貢獻率都較低。

4 結論

通過對某正交異性橋面板鋼箱梁橋動態稱重系統長期監測的車輛荷載數據進行統計分析，采用混合高斯模型擬合車重荷載分布概率密度，建立了該橋的疲勞車輛荷載譜，最后分析研究了各車型對該橋的疲勞損傷貢獻率，分析結果表明：

1)基于長時間的數據采集和分析，發現各周的車流量變化顯著，每周車流量的車型構成也有很大變化，其中兩軸車和六軸車占比變化最明顯，且這兩類型車的占比趨勢基本相反。長期的統計數據可以減小偶然因素帶來的影響，從而使研究更具有代表性和普遍性，所以有必要對長期車流情況進行研究。

2)各車型的車重概率密度分布均服從混合高斯分布，且由赤池信息準則和貝葉斯信息準則確定高斯分量數后的擬合曲線其和方差均接近于0，確定系數均大于0.96，可知擬合效果較好。

3)通過建立各車型疲勞荷載譜可知，V3型車第3軸的等效軸重與各類車型的等效軸重相比都最大，除此之外的各車型等效軸重相差都不明顯，但是隨著軸數的增加，等效車重也隨之增大，所以V2型車等效車重最小，V6型車最大。

4)六軸車各等效軸重產生的總疲勞損傷貢獻率最高，三軸車其次，兩軸車僅次于三軸車，四軸車和五軸車最低。原因是六軸車頻率較高，各軸的等效軸重也較大，且軸數多，再加上等效軸重相比于車流量更加影響疲勞損傷貢獻率的計算，導致疲勞損傷貢獻率最高和最不利車型都是六軸車。