基于卡爾曼濾波重構GRACE-FO姿態數據

梁磊，閆易浩，王長青，朱紫彤，高銘，鐘敏，于錦海，徐煥

1 中國科學院精密測量科學與技術創新研究院大地測量與地球動力學國家重點實驗室,武漢 430077 2 地理信息工程國家重點實驗室，西安 710054 3 中山大學物理與天文學院，廣東珠海 519082 4 中山大學測繪科學與技術學院，廣東珠海 519082 5 中國科學院大學地球與行星科學學院，北京 100049

0 引言

GRACE-FO（GRACE Follow-On）是GRACE（Gravity Recovery and Climate Experiment）的后續衛星，于2018年5月22日成功發射（Kornfeld et al.,2019）.二者是同類型衛星，通過精確測量兩顆衛星之間的距離反演地球時變重力場模型，研究地球質量變化（Tapley et al.,2004）.GRACE-FO相較于GRACE而言除了搭載K波段微波測距系統外，還首次實現了激光干涉測距，實現了以nm級的精度測量兩顆衛星之間的距離（Goswami et al.,2021）.GRACE與GRACE-FO的數據產品分為Level-0、Level-1A、Level-1B和Level-2，其中Level-0至Level-1B稱為載荷數據處理，Level-1B至Level-2稱為時變重力場反演（Wu et al.,2006;Case et al.,2010;Wen et al.,2019）.

在載荷數據處理過程中，GNSS（Global Navigation Satellite System）接收機、加速度計和星間測距等數據處理與姿態數據有關，主要為：第一個是計算KBR（K-Band Ranging）天線相位中心改正和GNSS天線相位中心改正，將測量的信息改正到衛星質心上；第二個是將加速度計（ACC，Accelerometer）測量的非保守力轉換到慣性坐標系；第三個是標定KBR天線相位中心位置和衛星質心位置；第四個是評估激光測距系統的耦合噪聲.姿態數據誤差會通過這四個方面傳遞到重力場模型中，例如Inácio等（2015）分析GRACE星間距變率殘差與KBR天線相位中心改正時，指出姿態誤差占總誤差的18%左右；Horwath等（2011）通過KBR天線相位中心改正，指出姿態誤差導致了星間指向存在偏差，通過對姿態誤差進行建模提高了重力場模型解算精度；Wegener等（2020）通過姿態數據評估了激光反射棱鏡交點與衛星質心不重合對激光測距的影響.因此確定高精度的重力衛星姿態數據是原始載荷數據處理的重要內容之一.

GRACE與GRACE-FO均搭載了星敏感器和慣性測量單元測量衛星的姿態，但二者又有較大區別.對于GRACE而言，每顆衛星上均搭載了兩顆星敏感器和一個三軸的慣性測量單元.星敏感器固定安裝于衛星左右兩個面上，三軸的慣性測量單元固定安裝于衛星的內部.然而，在發射之初GRACE-A星的慣性測量單元一個軸出現故障，未有冗余觀測量，GRACE-B星的慣性測量單元僅在備份模式下開啟（Bandikova,2015），所以兩顆衛星均未有IMU的測量數據，因此GRACE衛星姿態主要由星敏感器提供.受日月光照的影響GRACE只有一顆星敏感器或者無星敏感器測量衛星姿態，從而導致衛星姿態精度降低或出現大量間斷.借鑒于GRACE上的經驗，GRACE-FO在設計之初采用了三顆星敏感器和一個四軸光纖陀螺儀設計方案.相較于GRACE而言，三顆星敏感器設計方案減少了姿態數據間斷，并且較多的時間存在兩顆星敏感器測量衛星的姿態，部分時間有三顆星敏感器測量衛星姿態；四軸光纖陀螺儀具有更好的測量性能，固定安裝于衛星的內部，同時整個科學任務階段均可觀測（Kornfeld et al.,2019）.

融合多個載荷數據，提高最終數據產品處理精度，是目前數據處理常用的方法.對于GRACE而言，除了星敏感器測量衛星姿態數據外，加速度計可以同步測量衛星的角加速度數據，融合星敏感器數據和角加速度數據，可以提高姿態數據精度，彌補星敏感器數據的缺失，減少姿態數據間斷.例如Klinger（2018）在反演重力場模型時，首先基于最小二乘配置法融合了這兩類數據，構建了高精度的姿態數據產品；Goswami等（2018）組合了星敏感器與角加速度計數據，提高了姿態數據產品的精度；官方機構JPL（Jet Propulsion Laboratory）基于Kalman濾波融合了這兩類數據，發布了RL03版本的姿態數據（Harvey and Sakumura,2019）.GOCE衛星是另一顆用于地球重力場研究的衛星，其上搭載了引力梯度儀，測量地球引力梯度數據，可同步獲得測量頻段內的角加速度.由于在處理梯度數據時，需要改正的離心力項與衛星的角速度是非線性關系（Stummer et al.,2011;Pail,2005；郭澤華等，2021；趙宇鵬等，2021），這就需要高精度的姿態信息，由此需要融合星敏感器和梯度儀測量的角加速度數據.例如Cesare等（2008）在時域上通過Kalman濾波融合了這兩類數據；Stummer等（2011）和郭澤華等（2021）在頻率域上，基于Wiener濾波融合了這兩類數據.對于GRACE-FO而言，星敏感器和IMU是測量衛星姿態的主要載荷，其中星敏感器對姿態的低頻部分敏感，IMU對姿態的高頻部分敏感，融合這兩類數據可以獲得高精度的姿態數據.在時域上進行數據融合具有一定的便利性，可以同步評估IMU的漂移參數，彌補微小的間斷，因此本文選擇在時域下進行星敏感器數據與IMU數據融合.

關于姿態Kalman濾波，Lefferts等（1982）基于狀態變量（四元數和陀螺儀的漂移參數）的一階導形式構建了姿態Kalman濾波算法，此時在計算狀態轉移矩陣和狀態轉移方程時，其形式了變成了Riccati方程；Trawny和Roumeliotis（2005）與Lefferts方法類似，只是推導過程將Riccati方程變成級數形式.目前關于這種方法尚未有研究應用于實際的GRACE-FO數據處理中.Harvey和Sakumura（2019）將角速度近似處理轉換成四元數形式微小變化量作為Kalman濾波的狀態轉移矩陣，并基于此方法解算了GRACE和GRACE-FO的姿態數據，這種近似處理過程理論上具有一定的瑕疵.本文將以四元數和陀螺儀的漂移參數作為狀態變量，直接構建另一種姿態Kalman濾波融合算法，處理GRACE-FO的姿態數據.鑒于此，本文開展了GRACE-FO高精度的姿態數據處理的研究.在本文的第1節是介紹星敏感器處理算法、IMU處理算法和姿態Kalman濾波算法；第2節是分析姿態數據處理結果；第3節是評估姿態數據產品對時變重力場的影響；第4節是結論和總結.

1 理論方法

GRACE-FO搭載的三顆星敏感器和IMU記錄的時標是OBC（Onboard Computer）時標，首先需要利用TIM1B和CLK1B數據將OBC時標改正到GPS（Global Position System）時標上.其次對2 Hz采樣的多星敏感器數據進行組合并降采樣至1 Hz，然后通過姿態Kalman濾波與8 Hz采樣的IMU數據進行融合，輸出1 Hz姿態數據產品.下面分別介紹星敏感器數據處理、IMU數據處理和姿態Kalman濾波算法，其中星敏感器數據處理和IMU數據處理中的詳細細節可參考Yang等（2022）.

1.1 星敏感器數據處理

星敏感器測量的噪聲具有各向異性的特點，即繞垂直于星敏感器視軸方向旋轉的精度要比繞視軸方向旋轉的精度大約高8～10倍（Bandikova and Flury,2014;Stanton,2000）.由于在重力場反演過程中，需要的是SRF （Science Reference Frame）坐標系下的衛星姿態數據.為此，需要將星敏感器坐標系下測量的四元數轉換到SRF坐標系中，其中星敏感器坐標系與SRF的之間的轉換矩陣（即星敏感器安裝矩陣）記錄于QSA1B或者SOE文件中.轉換過程可看成是一個線性組合的形式，繞星敏感器視軸旋轉的精度低會傳遞到繞科學坐標系Y軸和Z軸旋轉中，導致繞這兩個軸旋轉的精度降低.融合多個星敏感器數據可以降低這一影響.目前，多星敏感器融合主要有兩種方法.第一種是根據星敏感器測量的噪聲構建權陣，通過加權的形式融合多星敏感器數據（Romans，2003）.第二種是利用星敏感器的視軸構建一個共同參考框架融合多星敏感器數據（Mandea et al.,2010）.這兩種方法均已用于多種衛星，例如CHAMP（Challenging Minisatellite Payload）、GRACE、GRACE-FO和GOCE（Gravity field and steady-state Ocean Circulation Explorer）（Bandikova and Flury,2014;Siemes,2011;Stummer et al.,2011）.對于這兩種方法而言，融合后的姿態數據精度基本一致（Bandikova,2015）.本文選擇使用第一種方法，融合多個星敏感器的測量值，相關算法具體參考Romans（2003）.

四元數運算有別于實數運算，需要采用合適的插值算法保證插值后的姿態具有很好的光滑性.本文采用單位四元素插值樣條曲線對四元數進行插值，保證插值后的衛星姿態具有二階導連續特點（邢燕等，2017），具體公式為

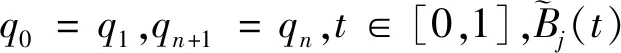
1.2 慣性測量單元數據處理

GRACE-FO的慣性測量單元是由4個四面體形式的光纖陀螺組成，每個光纖陀螺在其自身的陀螺儀框架下記錄濾波角（filtered angle），采樣率為8 Hz（Wen et al.,2019）.由于IMU記錄的每個軸采樣時刻并不一致，需要對每個軸的時間進行統一.IMU記錄的濾波角的范圍是從-5758°到5758°，當記錄到5758°時自動調整到-5758°開始，或與之相反.然而這導致對濾波角進行數值差分計算角速度時，存在異常情況，需要對異常情況進行處理.對于數值差分計算，為了保證數值差分計算的精度，本文選擇使用Diebel（2006）的方法，具體形式如下：

（1）

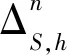
由于IMU測量存在冗余觀測，需要對冗余觀測量進行處理，根據Jafari（2015）指出同時融合冗余觀測量，可以提高角速度的精度，處理方法如下：

ω=（HTH）-1HTm，

（2）

其中，H4×3是一個轉換矩陣，表示的是4個光纖陀螺儀測量軸在IMU坐標系下的矢量，記錄于GRACE-FO Level-1A數據使用手冊中（Wen et al.,2019），m是陀螺儀的角速度測量值，ω是IMU坐標系下角速度.

1.3 姿態Kalman濾波方法

四元數運動方程可寫成如下形式（秦永元，2014）：

（3）

其中q是四元數矢量，其運算法則按照附錄A的形式計算，ω=[ωx,ωy,ωz]，對四元數微分方程組（3）按照角增量的形式進行求解，省略中間求解過程，可得：

q（t+1）=Φ（ωΔt）q（t），

（4）

其中

（5）

（6）

陀螺儀的噪聲模型可以寫成如下的形式（Lefferts et al.,1982）

（7）

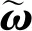
E[εω]=0，

（8）

E[εω（t1）,εω（t2）]=Q1（t）δ（t1-t2），

（9）

（10）

（11）

δ是克萊羅符號，Q1與Q2是相應的協方差.將公式（7）代入到公式（4）中，可以寫成

（12）

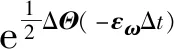
（13）

將公式（12）和（13）代入到公式（4）中，有

X（t+1）=f（t,X（t））+G（t）W（t），

（15）

那么f（t,X（t））可以寫成如下形式：

（16）

根據附錄公式（A3），G（t）W（t）可以寫成

（17）

對公式（17）進行泰勒展開，保留線性形式有

（18）

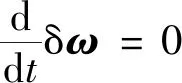
（19）

四元數的觀測方程來源于星敏感器，有

Z（t）=HX（t）+vk，

（20）

其中H=[I，0]，狀態轉移矩陣可以寫成

（21）

基于擴展Kalman濾波，姿態Kalman濾波算法過程按照以下五步進行：

第一步：狀態預測方程

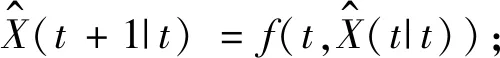
（22）

第二步：協方差矩陣預測

P（t+1|t）=Φ（t+1|t）P（t|t）ΦT（t+1|t）+Q（t+1）；

（23）

第三步：計算姿態Kalman濾波增益

K（t+1）=P（t+1|t）HT（t+1）[H（t+1）P（t+1|t）×HT（t+1）+R（t+1）]-1

（24）

第四步：狀態更新

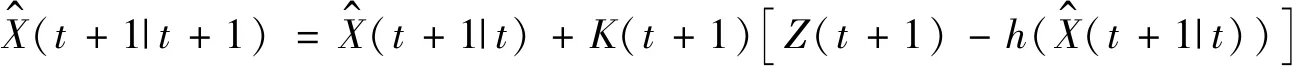
（25）

第五步：協方差更新

P（t+1）=[I-K（t+1）H（t+1）]P（t+1|t）.

（26）

2 結果分析

為了對處理后的姿態數據的精度進行評估，本文將與JPL發布的GRACE-FO Level-1B姿態產品進行對比分析，即SCA1B數據.對比分析的方法主要為星間指向（inter-satellite pointing）和衛星角速度矢量.星間指向為KBR天線相位中心矢量與LOS（Light of Sight）矢量的偏差并用角來表示，其中LOS為兩顆衛星質心之間的連線方向上的矢量通過軌道數據計算（Bandikova et al.,2012;Bandikova，2015）.星間指向主要是用于衛星在軌運行期間，監測兩顆衛星的對準情況，是判斷是否需要進行在軌控制的依據.由于直接計算慣性坐標系下衛星的姿態角，會受到較大值的影響難以展示相關細節，因此為了便于直觀展示解算的最終結果，本文采用星間指向進行對比分析.衛星角速度矢量用于評估融合后的姿態數據在中高頻部分是否完全融合了IMU信息.

星間指向計算過程如下：

（27）

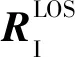
（28）

求解的φ、θ和ψ即為星間指向上的偏差角.

由于官方機構并未公布Level-0數據，僅公布了Level-1A和Level-1B數據，因此本文將從Level-1A數據出發構建GRACE-FO的姿態數據.本文選擇以2019年1月1日的數據為例，對星敏感器數據處理以及與IMU數據進行姿態Kalman濾波融合，并對濾波后的結果進行對比分析.

2.1 星間指向

首先選擇2019年1月1日中三顆星敏感器同時存在觀測數據的時間段進行分析.單個星敏感器解算的衛星姿態結果如圖1所示，其中SCA1、SCA2和SCA3表示星敏感器的編號（Kornfeld et al.,2019）.從星間指向的Yaw方向可見，即圖1中第一行，三個星敏感器的時間序列變化并不一致但基本維持在±1×10-3rad之間，從功率譜上看三個星敏感器在高頻部分的精度基本一致.從星間指向的Pitch方向可見，即圖1中第二行，三個星敏感器的時間序列變化基本維持在±1×10-3rad之間，并且SCA2和SCA3基本一致且有較多毛刺，而SCA1變化更加平滑.從功率譜上看SCA2和SCA3在高頻部分的精度基本一致，而SCA1具有更低的高頻噪聲.這主要是由于SCA1安裝在衛星的天頂方向，星敏感器視軸方向剛好與科學坐標系的Z軸平行，而SCA2和SCA3安裝在衛星左右兩個面方向上，從星敏感器坐標系轉換到SRF坐標系過程中，受到繞視軸旋轉不精確的影響傳遞到Pitch方向上.從星間指向的Roll方向可見，即圖中第三行，三個星敏感器的時間序列變化趨勢基本一致，從功率譜上看三個星敏感器在高頻部分精度處于同一水平.

融合多個星敏感器計算的星間指向的結果如圖2所示，其中SCA12、SCA13、SCA23和SCA123表示融合不同的星敏感器，例如SCA12表示融合SCA1和SCA2兩個星敏感器，SCA123表示融合SCA1、SCA2和SCA3三個星敏感器.從星間指向的Yaw、Pitch和Roll方向的時間序列可見，三個時間序列的變化趨勢基本一致.從功率譜上看，與圖1中的功率譜對比可見，融合多個星敏感器可以提高高頻部分的精度，并且融合三顆星敏感器解算的姿態的高頻部分的精度要略優于融合兩顆星敏感器的結果.此外，從星間指向的Pitch方向可發現一個有趣的現象，融合不同星敏感器計算的Pitch角存在一個偏差，最大相差約3.0×10-4rad.我們檢查了相應的計算流程，發現QSA1B中記錄的星敏感器坐標系與SRF坐標系的轉換四元數僅提供了地面標定值，未提供在軌標定值.對比GRACE的SOE文件可見，在GRACE入軌后進行了數次在軌標定，提供了相應的星敏感器坐標系與SRF坐標系轉換四元數.目前，由于缺少相關的遙測數據，無法驗證這樣的偏差是否來源于QSA1B，因此在本文的后續處理過程中，暫不考慮這樣的微小偏差影響.

融合星敏感器數據與IMU數據解算衛星姿態數據，其中首先對星敏感器數據進行融合并降采樣至1 Hz，然后再與8 Hz的IMU數據進行姿態Kalman濾波融合，在姿態Kalman濾波過程中僅保留整數秒的姿態數據.融合后的衛星姿態數據結果如圖2所示，其中APM表示本文所處理的姿態數據結果，JPL表示官方機構解算的結果.從星間指向的時間序列上看，Yaw、Pitch和Roll的時間序列趨勢變化基本一致，僅在Pitch方向上存在一個小的偏差，約為0.6 mrad.從功率譜看上基本一致，僅在截尾部分（即0.2～0.5 Hz處）JPL略低，這里將在后面進一步分析.

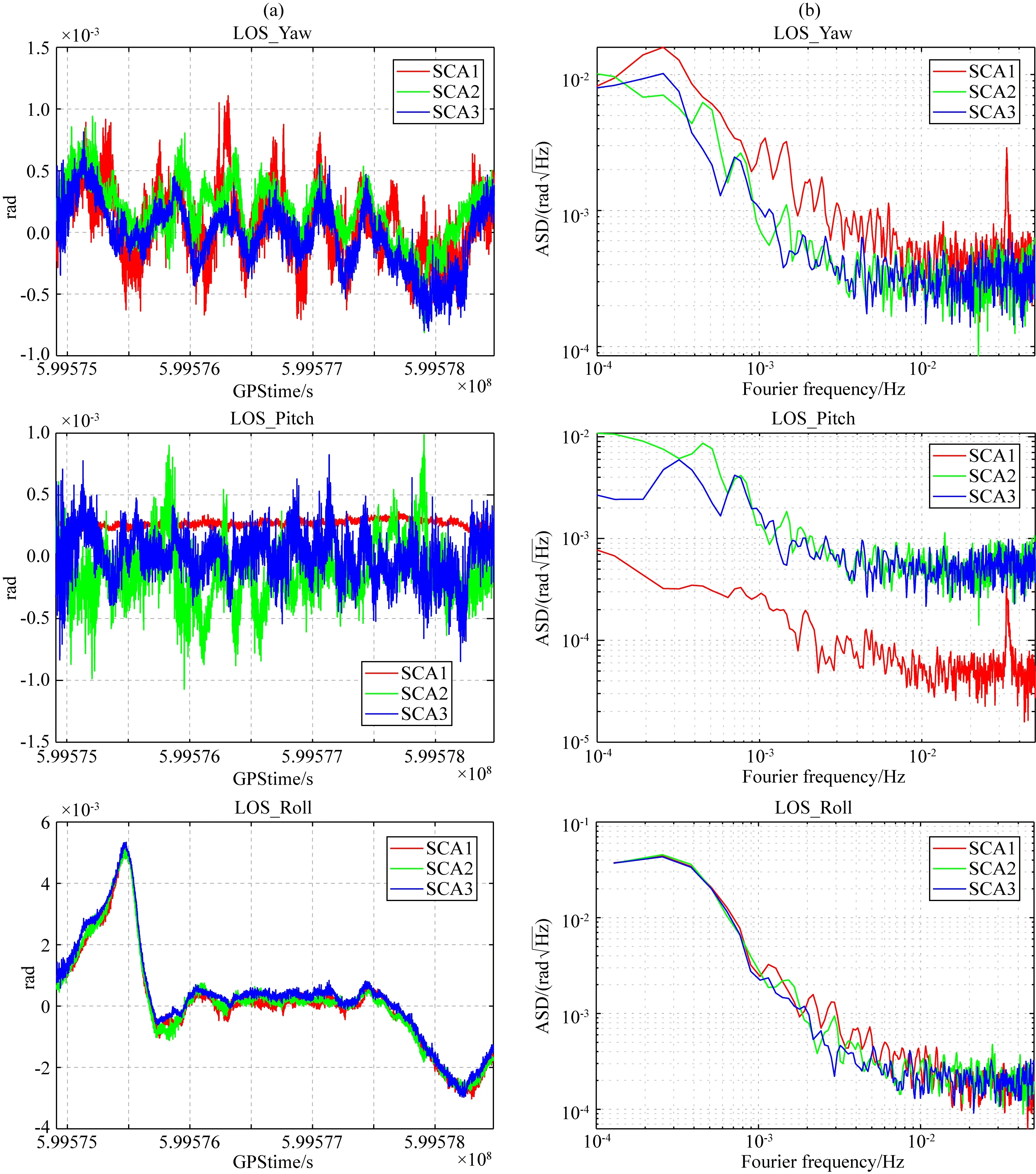
圖1 單個星敏感器解算的衛星姿態（a） 左列是星間指向的時間序列，（b） 右列是對應的功率譜，其中第一至三行分別表示星間指向的Yaw、Pitch和Roll三個方向.Fig.1 Satellite attitude calculated by a single star camera（a） The left plots are the time series of inter-satellite pointing,and （b） the right plots are the corresponding amplitude spectral density,where the first to third rows represent the Yaw,Pitch,and Roll directions of the inter-satellite pointing,respectively.

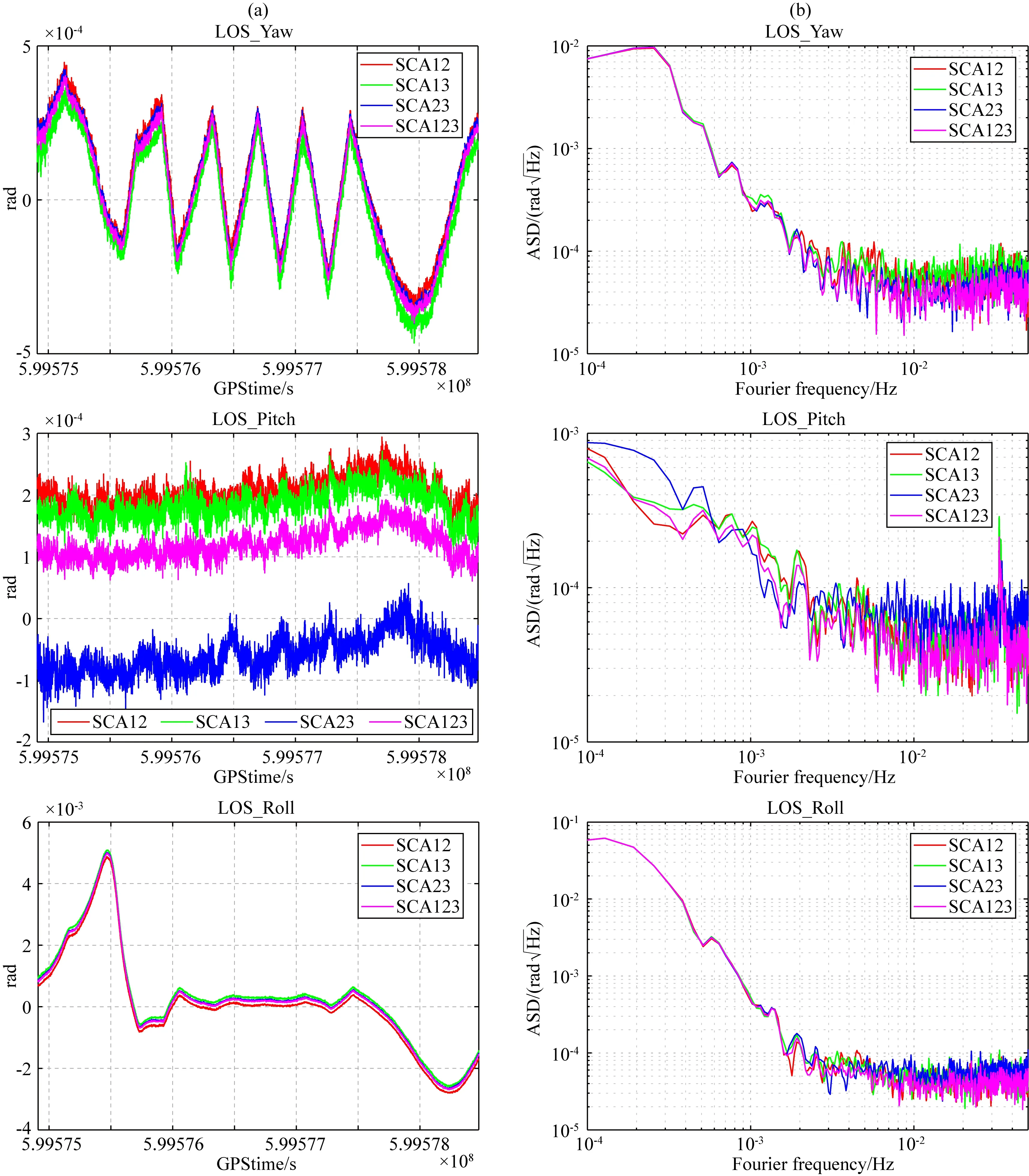
圖2 融合多個星敏感器解算的衛星姿態（a） 左列是星間指向的時間序列，（b） 右列是對應的功率譜，其中第一至三行分別表示星間指向的Yaw、Pitch和Roll三個方向.Fig.2 Satellite attitude calculated by fusing multiple star cameras（a） The left plots are the time series of inter-satellite pointing,and （b） the right plots are the corresponding amplitude spectral density,where the first to third rows represent the Yaw,Pitch,and Roll directions of the inter-satellite pointing,respectively.

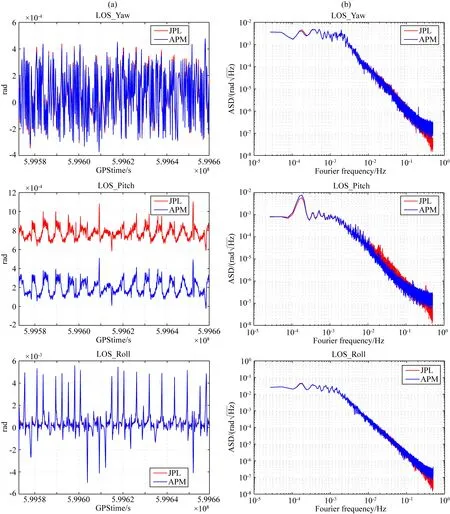
圖3 星間指向的分析（a） 左列表示相應星間指向的時間序列，（b） 右列表示相應的功率譜，其中第一至三行分別表示星間指向的Yaw、Pitch和Roll三個方向.Fig.3 Analysis of inter-satellite pointing（a） The left plots are the time series of inter-satellite pointing,and （b） the right plots are the corresponding amplitude spectral density,where the first to third rows represent the Yaw,Pitch,and Roll directions of the inter-satellite pointing,respectively.

圖4 衛星角速度矢量的分析（a） 左列表示時間序列，（b） 右列表示相應的功率譜，其中第一至三行分別表示ωx、ωy和ωz三個方向.Fig.4 Analysis of satellite angular velocity vector（a） The left plots are the time series of inter-satellite pointing,and （b） the right plots are the corresponding amplitude spectral density,where the first to third rows represent the ωx,ωy,and ωz.

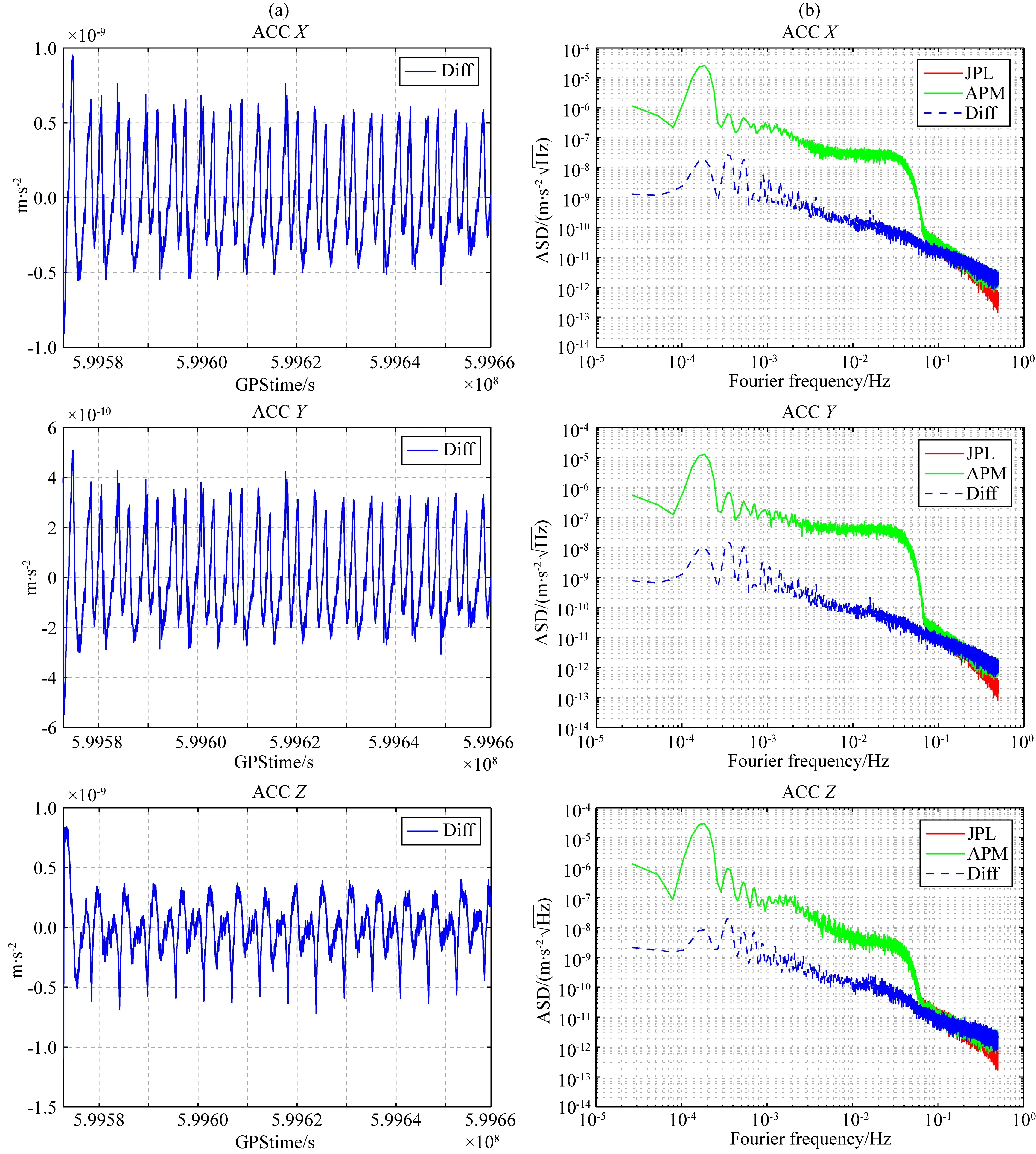
圖5 慣性坐標系下非保守力的比較（a） 左列表示APM與JPL姿態產品計算的非保守力差異的時間序列，（b） 右列是相應的功率，其中第一行至第三行分別表示慣性坐標系下X，Y和Z方向.Fig.5 Comparison of non-conservative forces in an inertial coordinate system（a） The left plots represent the time series of non-conservative force differences calculated by the APM and JPL attitude data,（b） the right plots represent the corresponding amplitude spectral density,where the first to third rows represent the X,Y,and Z directions of the inertial coordinate system.

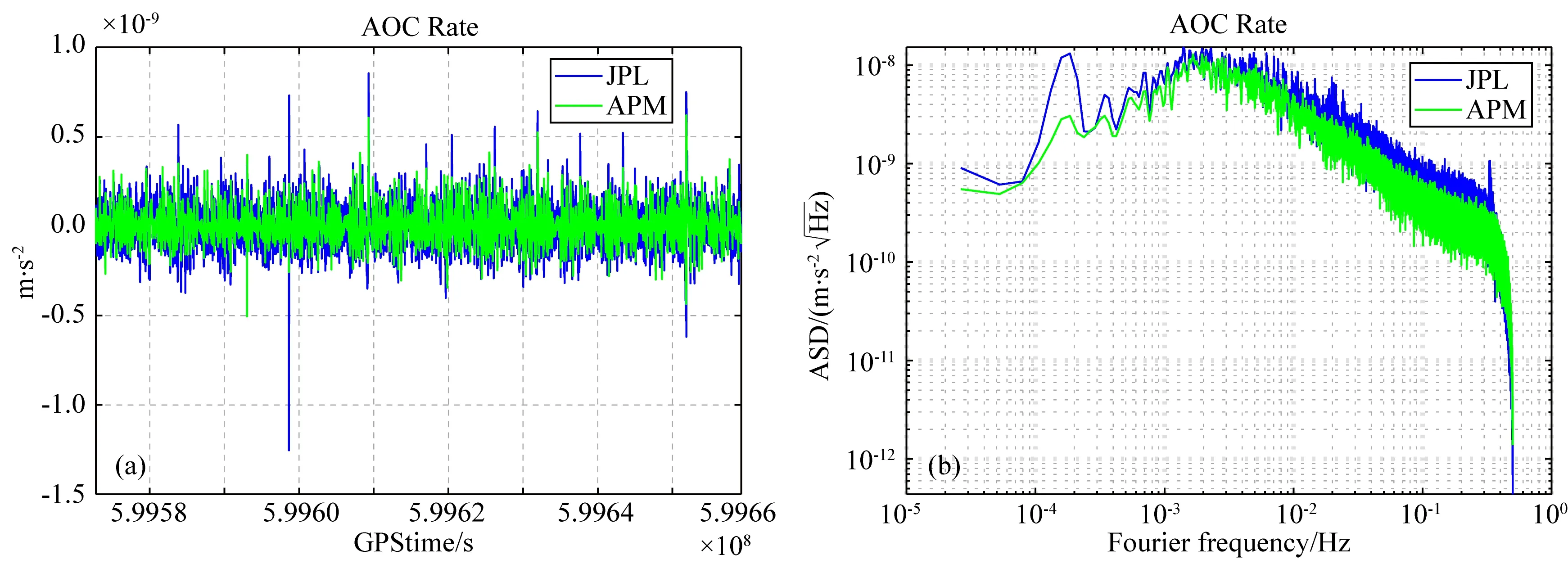
圖6 KBR天線相位中心改正變率（a） 時間序列;（b） 相對應的功率譜.Fig.6 KBR antenna phase correction rate（a） The time-series;（b） The corresponding amplitude spectral density.

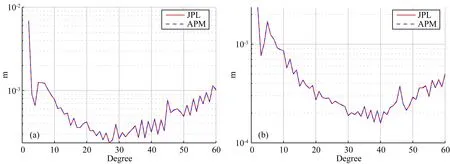
圖7 時變重力場模型的階方差（a） 2018年6月;（b） 2019年3月.Fig.7 The degree variance of the time-variable gravity field model（a） The June 2018;（b） The March 2019.

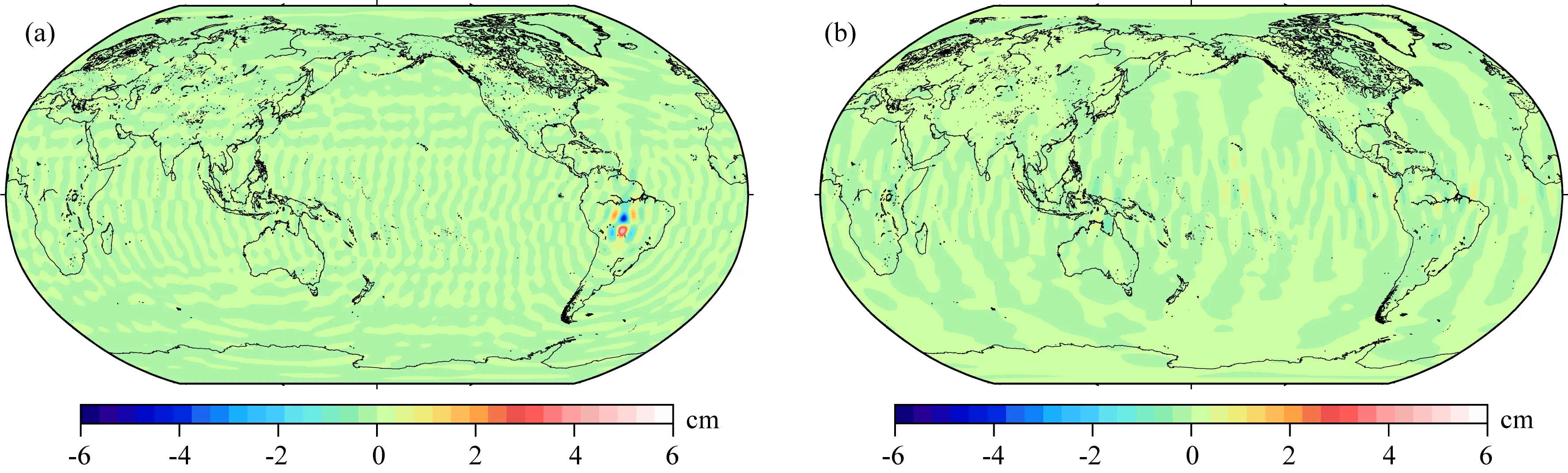
圖8 質量變化等效水高（a） 2018年6月；（b） 2019年3月.Fig.8 The equivalent water height for mass change（a） June 2018；（b） March 2019.

2.2 衛星角速度

利用公式（3）計算衛星的角速度驗證進行比較，結果如圖4所示.圖4中APM、JPL和IMU1B分別表示本文解算的結果、官方機構結果和IMU測量的角速度.APM-IMU1B、JPL-IMU1B分別表示APM和 JPL計算的角速度與IMU1B測量值的差異.為了更好的展示細節，在圖4的左列中僅展示了2019年1月1日前10000秒的時間序列，其中相對應的功率譜則使用完整的一天數據進行計算.從圖4的時間序列可見，{ωx,ωy,ωz}變化趨勢基本一致，APM與IMU1B的差異在三個軸的標準差分別為1.89×10-7rad·s-1，1.56×10-7rad·s-1，1.63×10-7rad·s-1，JPL與IMU1B的差異在三個軸的標準差分別為6.09×10-7rad·s-1，3.62×10-7rad·s-1，4.01×10-7rad·s-1，可見APM相較于JPL而言精度至少提高了3倍，具有更高的精度.從功率譜上看，APM、JPL和IMU1B變化基本一致，但是從與IMU1B產品的差異上看，APM在0.004～0.2 Hz上具有更低的噪聲，特別在0.01～0.1 Hz相較于JPL而言噪聲水平低一個量級左右，即圖中青色虛線低于品紅色虛線.換句話說本文所解算的姿態數據充分融合IMU1B數據，具有更低的噪聲水平.在截尾部分（即0.2～0.5 Hz處）可見，APM與JPL都有明顯的下降趨勢，這與濾波所選取的截止頻率有關.

3 對時變重力場的影響

正如引言所述，姿態數據主要通過非保守力轉換和KBR天線相位中心改正影響重力場模型解算精度.因此，本節將對比分析APM和JPL姿態數據對非保守力轉換以及KBR天線相位中心改正的影響，并進一步反演時變重力場模型分析姿態數據對時變重力場模型精度的影響.時變重力場反演的過程及等效水高計算過程本文參考Liang等（2021）、梁磊等（2019）和Zhou等（2018）.

計算慣性坐標系下非保守力的結果如圖5所示.由于只需要評估APM與JPL姿態數據計算慣性坐標系下非保守力的差異，因此在圖5左列中的時間序列只展示了轉換后的非保守力的差異，在圖5的右列中展示了JPL與APM轉換后的非保守力及其差異的功率譜.對圖5中的時間序列進行統計，結果如表1所示.從圖5左列的時間序列和表1可見，通過APM和JPL姿態數據轉換后的非保守力差異的標準差在10-10m·s-2左右，非保守力差異的均值在X和Y軸的方向為10-11m·s-2左右，在Z軸的方向均值差異為4.61×10-10m·s-2，也就是說在6 h積分弧長上，非保守力的差異累積不超過2 cm，低于定軌精度.從圖5右列的功率譜上看高頻部分的差異主要受姿態數據的影響，低頻部分主要是集中于1CPR和2CPR.對于1CPR和2CPR的低頻信號，在重力場反演過程中可看成是低頻誤差（Liang et al.,2021;Kim,2000;Zhao et al.,2011;Zhou et al.,2018,2019），通過低頻誤差處理或者加速度標定進行吸收，并不影響重力場模型解算精度.

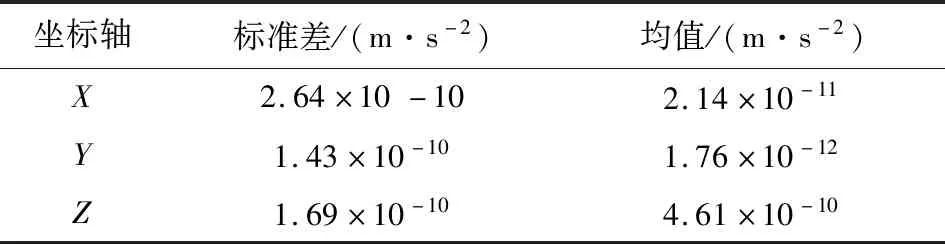
表1 轉后非保守力差異的標準差和均值Table 1 Standard deviation and mean of the non-conservative force difference

由于在反演重力場過程中，主要使用的是星間距變率作為觀測值，因此這里僅計算KBR天線相位中心改正變率進行分析，計算方法參考Bandikova（2015），結果如圖6所示.從圖中可見，KBR天線相位中心改正的時間變率量級在10-9m·s-1左右，遠低于KBR測距精度1 μm·s-1的要求，因此KBR天線相位中心改正的時間變率對重力場反演影響很小.此外，可見GRACE-FO對兩顆衛星的對準情況要求要更為嚴格.

選取2018年6月和2019年3月數據反演時變重力場模型進行比較，其中反演重力場過程中只考慮姿態數據的差異，其他數據則使用JPL Level-1B產品.反演時變重力場模型的階方差和等效水高結果如圖7—8所示.從圖7可見，反演時變重力場模型的階方差基本一致.圖8表示的是兩個模型計算的等效水高差異，從圖中可見在全球范圍內利用APM與JPL姿態數據計算的等效水高基本一致，僅在GRACE-FO任務開始階段（2018年6月），在質量變化較大的亞馬遜流域上有略微差異，約占最大信號的5%左右，進入到任務穩定時期（2019年3月），計算的全球等效水高基本一致.

4 結論

本文研究了GRACE-FO姿態數據Level-1A至Level-1B的處理算法及其對時變重力場的影響.首先根據GRACE-FO載荷設計特點，從四元數運動微分方程出發，以四元數和陀螺儀漂移參數為狀態變量，構建了一種新的姿態Kalman濾波融合算法.然后以GRACE-FO數據為基礎，分析了單個星敏感及多星敏感器組合對衛星姿態解算的影響，可見融合多星敏感器數據可以抑制高頻部分的噪聲.另外，星敏感器數據之間的偏差可能來源于官方機構未提供在軌標定的星敏感器安裝矩陣，需要進一步利用遙測數據進行分析驗證.最后基于本文推導的姿態Kalman濾波算法，處理實際的GRACE-FO Level-1A數據，從星間指向和角速度矢量可見，本文解算的姿態數據充分發揮了IMU載荷的性能，具有更低的噪聲水平，優于JPL解算的結果.

對時變重力場模型精度的影響，本文首先分析了姿態數據對轉換后的非保守力和KBR天線相位中心改正的影響.從轉換后的非保守力看，本文解算的姿態數據與JPL的姿態數據引起的差異在10-10m·s-2左右，從KBR天線相位中心改正上看，本文解算的姿態數據與JPL的姿態數據計算的KBR天線相位中心改正變率量級在10-9m·s-1，遠低于KBR星間變率1 μm·s-1的精度要求.進一步解算了2018年6月和2019年3月的時變重力場進行比較，從階方差和等效水高差異上看，本文解算的姿態數據與JPL的姿態數據對時變重力場模型的精度影響很小.總的來說，本文構建了一種的新的姿態Kalman濾波算法，解算的姿態數據充分發揮了IMU的性能精度優于JPL，但對時變重力場模型解算精度的影響很小，目前限制時變重力場模型的精度主要來源于其他誤差.

致謝感謝GFZ網站提供的GRACE-FO Level-1A和Level-1B數據（ftp:∥isdcftp.gfz-potsdam.de/grace-fo/）.感謝審稿專家對本文提出的寶貴修改意見.

附錄A 四元數的定義和運算

稱q=q0+q1i+q2j+q3k為一個四元數，其中q0,q1,q2,q3∈R，i,j,k是不同的虛數單位，滿足i2=j2=k2=-1，ij=-ji=k，jk=-kj=i，ki=-ik=j.四元數也可以表示成（q0,q1,q2,q3），其中q0是標量.

令任意三個四元數為q=（q0,q1,q2,q3），p=（p0,p1,p2,p3）和s=（s0,s1,s2,s3），那么四元數的運算法則定義如下.

加法：

q±p=（q0±p0,q1±p2,q1±p2,q1±p2），

（A1）

點乘：

q·p=q0p0+q1p1+q2p2+q3p3，

（A2）

乘法：

s=qp,

（A3）

共軛：

（A4）

模：

（A5）

若‖q‖=1，則稱q是單位四元數.

逆：

（A6）

單位四元數三角函數形式及指數形式：

q=cosθ+nsinθ，

（A7）

其中n∈S2為單位矢量.