重力異常垂向梯度嚴密改化模型及應用

黃謨濤，鄧凱亮，吳太旗，歐陽永忠，陳欣，翟國君，劉敏，王許

海軍研究院，天津 300061

0 引言

重力異常場是地球內部質量分布不均勻性及外部地形變化形態的綜合反映（Dehlinger,1978；Torge,1989）.利用地表重力觀測研究確定地球形狀大小及變化特性，是重力與大地測量學的核心任務,其研究內容包含大地測量邊值問題解算、局部和外部重力場逼近（Heiskanen and Moritz,1967；李建成等,2003；Sansò and Sideris,2013）；依據地表重力觀測研究確定地球內部物質結構、形態及物理特性，則是地球物理學的重要研究主題之一，其研究內容涉及利用數值計算方法解決地球重力場的正演和反演問題（Moritz,1990；馬在田等,1997）.由此可見，地球重力場研究不僅跨越了地球物理學和大地測量學兩個學科的研究領域，同時跨越了地球內部、地表及外部空間三個不同特征的研究空域，其研究內容除了涉及不同空域的多維度重力場建模技術外，還包含地表重力觀測數據的向上和向下延拓歸算技術（Moritz,1980；Cruz and Laskowski,1984；梁錦文,1989；王興濤等,2004；劉敏等,2018）.實際上，大地測量邊值問題解算和地球外部重力場逼近計算都可以歸結為廣義的重力位場向上和向下延拓問題（Moritz,1966；Heiskanen and Moritz,1967；Moritz,1980；于錦海等,2001；Sansò and Sideris,2017）.可見，重力向上和向下延拓技術在地球重力場研究中具有非常重要的應用價值.實施向上和向下延拓解算除了可以依托傳統的Poisson積分方程外（Heiskanen and Moritz,1967），還可以采用計算穩定性更好的Taylor級數展開模型（Peters,1949）.精確求取位場各階垂向導數（也稱垂向梯度）是運用Taylor級數展開延拓法的關鍵，國內外諸多學者為此提出了許多解決該問題的方法（Moritz,1980；劉保華等,1995；姚長利等,1997；Fedi and Florio,2002；Wei,2014；張沖等,2017；黃謨濤等,2018；Tran and Nguyen，2020）.實際上，除了向上和向下延拓解算，位場垂向梯度還可以直接應用于地質結構反演和地球資源勘探，因為重力梯度數據更能精細反映地球內部淺層地質結構密度的變化形態（王虎彪等,2009；劉金釗等,2013,2020）.

在前述各種應用中，重力異常一階垂向梯度是應用面最廣泛的重力場特征參數之一，在各類重力歸算和大地測量邊值解算中發揮著關鍵性作用（Heiskanen and Moritz,1967；Moritz,1980；Wang et al.,2012）.求解觀測重力異常的全球積分是獲取重力異常垂向梯度的主要手段，但實施此類積分模型數值計算時均涉及全球積分模型改化問題，一方面需要對全球積分計算式進行積分域分割處理，通常做法是將全球積分劃分為近區和遠區，近區采用實測數據進行數值積分計算，遠區則采用地球位模型進行補償（黃謨濤等,2020）；另一方面需要對積分核函數進行去奇異性處理，傳統做法是通過引入合適的積分恒等式變換，將原積分計算模型轉換為具有穩定數值解的連續函數模型（Heiskanen and Moritz,1967）.需要指出的是，在實際應用中，人們在實施全球積分域分割處理時，往往會忽視積分恒等式成立的全球積分條件，不再關注采用局域積分對積分恒等式帶來的數值影響（Heiskanen and Moritz,1967；Moritz,1980；歐陽明達等,2014；翟振和等,2015；劉長弘,2016），從而引起不可忽略的計算誤差（黃謨濤等，2019）.考慮到重力異常一階垂向導數是計算二階及其更高階導數的基礎，本文主要針對球面及外部重力異常一階垂向導數全球積分模型改化問題進行分析研究和試驗驗證，依據實測數據保障條件和積分域分割處理方式，分別推出兩類參數全球積分模型的嚴密改化公式，同時通過數值計算和向下延拓應用對比分析，進一步驗證采用嚴密改化模型的可行性和有效性.

1 計算模型分析與改化

1.1 地球外部重力異常垂向梯度嚴密改化模型

由Heiskanen和Moritz（1967）得知，地球外部重力異常全球積分計算式可表示為

（1）

（2）

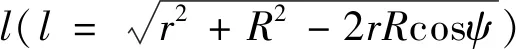
由式（1）不難看出，當計算點趨近于數據點時，即當r→R和ψ→0時，會出現分子分母項同時為零的不定式（0/0）情況，積分核函數K（r,ψ）發生奇異.為了消除積分式（1）的奇異性，通常做法是從積分域中直接扣除計算點所在的網格數據塊，從而避免出現積分核函數分母項l→0現象.這種處理方法看似比較簡單明了，但往往會給計算結果帶來不可忽略的誤差.為此，Heiskanen和Moritz（1967）建議采用式（3）表示的積分恒等式對式（1）進行改化：

（3）

略去推導過程，直接寫出改化公式如下：

（4）

式中，ΔgRp代表空間計算點P（r,φ,λ）在地面投影點P0（R,φ,λ）處的已知觀測值.式（4）即為人們常用的經去奇異性改化后的地球外部重力異常全球積分計算公式.從形式上不難看出，引入積分恒等式（3）變換后，計算式（4）不再存在積分奇異性問題，同時確保當r→R時，積分計算值Δgp收斂于球面觀測量ΔgRp.Heiskanen和Moritz（1967）認為，經式（3）變換后，至少可以說式（4）核函數的奇異性被中和了.于錦海等（2001）從理論上證明了式（4）右端奇異積分項在Chauchy主值意義下的存在性，從而為實施式（4）及其微分算子的數值計算提供了理論依據.

地球外部重力異常徑向偏導數計算模型可直接由式（4）求微分得到

（5）

依據式（5）可推出重力異常一階徑向偏導數Δg′rp計算模型為

（6）

=K1（r,ψ）.

（7）

如前所述，受觀測數據覆蓋范圍的限制，在實際使用式（6）計算地球外部重力異常一階徑向偏導數時，通常需要將全球積分域劃分為近區和遠區處理，近區定義為以計算點為中心、ψ0為半徑的球冠區域σ0，剩下的部分稱為遠區（σ-σ0）.一般以一定階次（比如N階）的重力位模型作為參考場，聯合采用實測重力數據和移去恢復技術，對近區數據影響進行數值積分計算；遠區效應則采用更高階次（比如L階）的重力位模型進行補償（黃謨濤等，2020）.引入基于參考場的“移去-恢復”處理模式后，還需要對積分核函數作相應的改化處理，以滿足積分核函數與觀測重力異常信息之間的頻譜匹配要求（Novák and Heck,2002；劉敏等，2016）.這里統一使用簡單實用的Wong和Gore（1969）方法對積分核函數進行改化，即從原核函數中截斷掉與位模型參考場相同階次的球諧展開式.經分區處理和核函數改化后，計算式（6）從全球積分模型轉換為局域積分模型，也就是第一步改化模型：

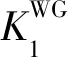
（8）

×Pn（cosψ），

（9）

（10）

（11）

（12）

（13）

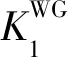
需要指出的是，式（8）并不是嚴密的改化模型，還不能作為最終的實用化公式使用.這是因為，式（8）是由全球積分式（6）改化為局域積分得來的，式（6）又是從積分恒等式（3）變換過來的，而恒等式（3）成立的前提條件是積分域覆蓋全球，由分區改化得來的計算式（8）對應的是局域積分，顯然不滿足積分恒等式（3）的假設條件要求.盡管在式（8）的右端已經通過超高階位模型計算值Δg′rq（σ -σ0）顧及了遠區效應的影響，但Δg′rq（σ -σ0）只代表式（8）右端積分項Δgq在遠區（σ-σ0）的補償，并未顧及另一積分項ΔgRp在遠區（σ-σ0）的影響.這就意味著，當我們采用局部區域觀測數據完成式（8）計算時，其計算結果必然存在一定大小的系統性模型偏差.數值試驗結果表明，要想獲得高精度的外部重力異常垂向梯度計算結果，必須消除該項誤差的影響.

從前面的分析得知，由全球積分過渡到局域積分引起計算式（8）的模型誤差可用公式表示為

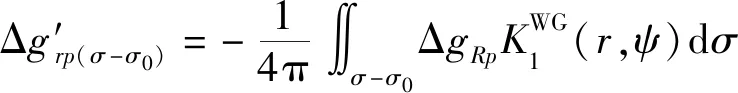
（14）

（15）

（16）

式中，Δg′rp（σ-σ0）代表ΔgRp在積分遠區（σ-σ0）對計算參量Δg′rp的影響.將式（7）代入式（15），并進行積分運算，可推得

+rRcosψ0（r2-5R2）]，

（17）

（18）

在式（8）右端加入模型誤差修正項Δg′rp（σ -σ0），可得到計算外部重力異常一階徑向偏導數的第二步改化模型：

+Δg′rq（σ -σ0）+Δg′rp（σ -σ0）.

（19）

按照同樣的思路可推得外部重力異常二階及以上高階偏導數相對應的改化公式，但考慮到由式（5）定義的高階偏導數涉及復雜的觀測函數連續性和核函數強奇異性問題，我們擬另文作專題研討，這里不再展開討論.需要指出的是，在重力異常場變化比較劇烈的區域，使用式（19）計算重力異常垂向梯度還會帶來一定的模型誤差.這是因為，在式（19）右端的積分項中，我們是把計算點所在的網格數據塊重力異常當作常值ΔgRp處理的，該數據塊對計算參量Δg′rp的影響已經在式（19）右端的第一項和最后一項中得到補償，在積分項中不再體現該數據塊的影響.但當計算點附近的重力異常場變化比較劇烈時，再將計算點所在數據塊當成常值處理可能帶來不可忽略的誤差，必須對其作相應的補償.假設與計算點重合的網格數據塊半徑為ψ00，考慮到該數據塊是一個很小的區域，故可采用極坐標系（s,α）對積分核函數作平面近似處理.取

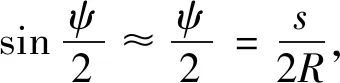
略去（h/R）2及以上高階項影響，可將由式（7）表示的積分核函數近似表示為

（20）

此時，計算點所在數據塊的積分式可寫為

（21）

式中，Δg′rp0代表計算點所在數據塊重力變化特征對計算參量Δg′rp的影響；s0代表數據網格大小的一半，當數據網格為1′×1′時，s0=0.5′.由式（21）得知，如果把中心數據塊的重力異常當成常值ΔgRp看待，即認為在計算點所在的數據網格內處處滿足Δgq=ΔgRp，則有Δg′rp0=0.當計算點附近的重力異常場變化比較劇烈時，可參照Heiskanen和Moritz（1967）的思路，將重力異常Δgq在空間計算點P的球面投影點Rp處展開為泰勒（Taylor）級數：

+…，

（22）

式中，x軸指向正北，y軸向東，x=scosα，y=ssinα.并且有

將式（22）代入式（21），同時考慮到修正項Δg′rp0本身的量值一般比較小，Taylor級數展開式（22）中的三階及以上各項的綜合影響可以忽略不計（Heiskanen and Moritz，1967），由此不難推得

（23）

假設與計算點重合的數據格網為（i,j），可按式（24）、（25）計算gxx和gyy：

（24）

（25）

將式（23）加入式（19）的右端，就得到計算外部重力異常垂向梯度的嚴密改化模型：

+Δg′rq（σ-σ0）+Δg′rp（σ-σ0）+Δg′rp0.

（26）

1.2 地面重力異常垂向梯度嚴密改化模型

相比地球外部重力異常垂向梯度，在地球重力場逼近計算實際應用中，人們更關注的是地球表面或重力觀測面（近似為球面）上的垂向梯度.為此，這里專門給出球面重力異常一階徑向偏導數嚴密改化公式.

實際上，球面重力異常垂向梯度只是外部重力異常垂向梯度的一個特例.在式（6）和式（7）中，令r=R，可推得球面上的重力異常一階徑向偏導數Δg′Rp計算模型：

（27）

（28）

l0=2Rsin（ψ/2），

（29）

將式（28）代入式（27）得

（30）

式（30）就是重力歸算應用中最常見的球面重力異常一階徑向偏導數計算模型（Heiskanen and Moritz,1967）.

顯然，在實際應用中，同樣需要對式（30）右端的全球積分做分區改化處理，同時需要引入位模型參考場對已知參量和待求參量進行移去恢復計算和積分核函數截斷處理.基于與式（6）同樣的改化流程，首先將式（30）右端的全球積分改化為近區積分和遠區球諧函數展開兩部分：

（31）

（32）

（33）

式中，Δg′Rq（σ-σ0）代表球面重力異常一階徑向偏導數遠區效應位模型計算值；Qn（Δg′R）為相對應的Poisson積分核截斷系數；其他符號意義同前.很顯然，式（31）—（33）可以直接由式（8）—（11）令r=R得到.類似于式（8），經第一步改化后的式（31）同樣存在由全球積分過渡到局域積分引起的模型誤差，該誤差大小可由式（34）確定：

（34）

l0（ψ0）=2Rsin（ψ0/2），

（35）

式中，Δg′Rp（σ-σ0）代表ΔgRp在積分遠區（σ-σ0）對計算參量Δg′Rp的影響.同樣可以證明，式（34）可直接由式（14）令r=R得到.

在式（31）的右端加入模型誤差修正項Δg′Rp（σ -σ0），可得到計算球面重力異常一階偏導數的第二步改化模型：

顯然，計算球面重力異常一階偏導數的嚴密改化公式還應當包含與式（23）相對應的計算點所在數據塊的影響（Heiskanen and Moritz,1967）.在式（23）中令h=0（即r=R），可直接求得

（37）

式中，Δg′Rp0代表計算點所在數據塊重力變化特征對計算參量Δg′Rp的影響.式（37）與Heiskanen和Moritz（1967）的推導結果完全一致，將其加入式（36）的右端，就得到計算球面重力異常垂向梯度的嚴密改化模型：

+Δg′Rq（σ-σ0）+Δg′Rp（σ-σ0）+Δg′Rp0，

（38）

式中，Δg′Rq（σ-σ0）和Δg′Rp（σ-σ0）分別代表Δgq和ΔgRp在積分遠區（σ-σ0）對計算參量Δg′Rp的影響，分別由式（32）和式（34）計算；Δg′Rp0代表計算點所在數據塊對計算參量Δg′Rp的影響，由式（37）計算.后面的數值計算檢驗，將進一步驗證第一步改化公式（31）增加模型誤差兩個修正項Δg′Rp（σ-σ0）和Δg′Rp0的必要性及有效性.

1.3 重力異常垂向梯度向下延拓應用

如前所述，向下延拓是重力異常垂向梯度最重要的應用方向之一.除了我們常見的航空重力向地面延拓計算外（王興濤等,2004；黃謨濤等,2018），重力異常垂向梯度最具標志性的應用場景是，將地面重力異常延拓歸算到海平面或過計算點的水準面，進而用于大地測量邊值問題解算（Moritz,1980；于錦海等,2001）.實際上，基于現代邊值問題理論的Molodensky零階加一階項級數解可解釋為，首先將地面重力異常向下解析延拓到海平面，用Stokes積分求得海平面上的高程異常，再將該結果向上延拓到地面（Heiskanen and Moritz,1967；李建成等，2003）.其中，地面空間重力異常Δg向海平面延拓的計算公式可表達為

（39）

式中，Δg*代表海平面上的重力異常；h代表地面點的正常高；（?Δg/?h）為地面重力異常的垂向梯度，通常使用前面介紹的一階徑向導數（?Δg/?r）來替代.美國從20世紀90年代開始，每隔3至5年就會對作為國家高程基準的大地水準面模型進行更新換代，新發布的USGG2009模型在構建過程中，就使用了式（39）作為地面重力異常的歸算模型（Wang et al.,2012）.顯然，與完整的向下解析延拓模型相比較（Moritz,1980），式（39）已經事先省略了二次及更高次項的影響，關于這些高次項影響的討論已經超出本文的研究范圍，故不再做更多的評述，這里主要就一階徑向導數（?Δg/?r）計算模型的完備性對重力異常向下延拓精度的影響進行分析和驗證，具體見后面的數值計算檢驗環節.

2 數值計算檢驗與分析

2.1 數值檢驗使用的數據及區域

為了分析比較前述不同階段改化模型的計算效果，本文采用超高階位模型EGM2008作為數值計算檢驗的標準場（Pavlis et al.,2012），用于模擬產生球面1′×1′網格重力異常觀測量“真值”（這里使用1′×1′而非5′×5′網格數據是為了減弱積分離散化誤差的影響），同時產生球面及外部設定高度的重力異常垂向梯度理論“真值”.由重力位模型計算地球外部重力異常及一階徑向偏導數的公式為（Heiskanen and Moritz,1967；黃謨濤等，2005）

（40）

（41）

式中各個符號意義同前.在式（40）和（41）中令r=R，可得到計算地球表面（球面）重力異常及其一階徑向偏導數的公式.

為了體現檢驗結果的代表性，這里特意選取重力場變化比較劇烈的馬里亞納海溝作為試驗區，具體覆蓋范圍為：6°×6°（φ：10°N—16°N；λ:142°E—148°E）.首先選取截斷到360階次的位模型EGM2008作為參考場，即取N=360，然后選取361～2160階次的位模型EGM2008作為數值計算檢驗的標準場，即取L=2160，進而選取ri=R+hi，R=6371 km，使用EGM2008模型（361～2160階次）分別計算標準場7個高度面上的1′×1′網格重力異常觀測量“真值”Δgti及相對應的一階徑向偏導數理論“真值”Δg′ti（i=1,2，…，7）,每一個高度面對應360×360=129600個網格點數據，7個高度分別為：hi=0 km,0.1 km,0.3 km,1 km,3 km,5 km,10 km.表1列出了其中5個高度面的理論“真值”統計結果，圖1和圖2分別給出了對應于零高度面的重力異常及其一階徑向偏導數理論“真值”的分布態勢.

表1統計結果和圖1、圖2顯示的重力異常及一階徑向偏導數變化形態說明，盡管已經扣除掉2～360階次頻段的參考場，本試驗區域標準場重力變化的激烈程度仍然非常顯著，可在一定程度上代表真實地球大部分局部重力場的變化特征.

表1 由EGM2008模型（361～2160階次）計算得到的重力異常及其一階導數統計結果Table 1 Gravity anomalies and their first order derivatives obtained by the EGM2008 model of degree 361～2160

2.2 垂向梯度改化模型檢驗結果分析

為了對比分析不同改化模型的計算效果，這里首先采用零高度面上的1′×1′網格重力異常“真值”Δgt0作為觀測量，同時使用前述4種地球外部重力異常垂向梯度（Δg′rp）改化模型，對前面選定的試驗區對應于7個高度面上的1′×1′網格重力異常一階偏導數進行數值計算檢驗和分析，其中，第1模型是指直接對式（1）求徑向偏導數作為基礎計算模型，并對全球積分域作了分區處理，但在實施近區計算時，扣除掉與計算點重合的那個1′×1′數據塊，以避免出現奇異積分；第2模型對應于公式（8）；第3模型對應于公式（19）；第4模型對應于公式（26）.將4種改化模型的計算值分別與相對應高度面的理論“真值”Δg′ti作比較，可獲得不同改化模型的精度評估信息，具體比對結果列于表2.這里積分半徑統一取為ψ0=2°，為了減小積分邊緣效應對評估結果的影響，表2只列出中心區2°×2°方塊內的比對結果（下同）.為了定量評估由全球積分過渡到局域積分引起的模型誤差影響，這里同時給出了采用式（14）計算得到的兩組分別對應于ψ0=2°和ψ0=5°的誤差補償量Δg′rp（σ-σ0）統計結果，具體見表3，該補償量是本文推出的嚴密改化公式中最重要的修正項.

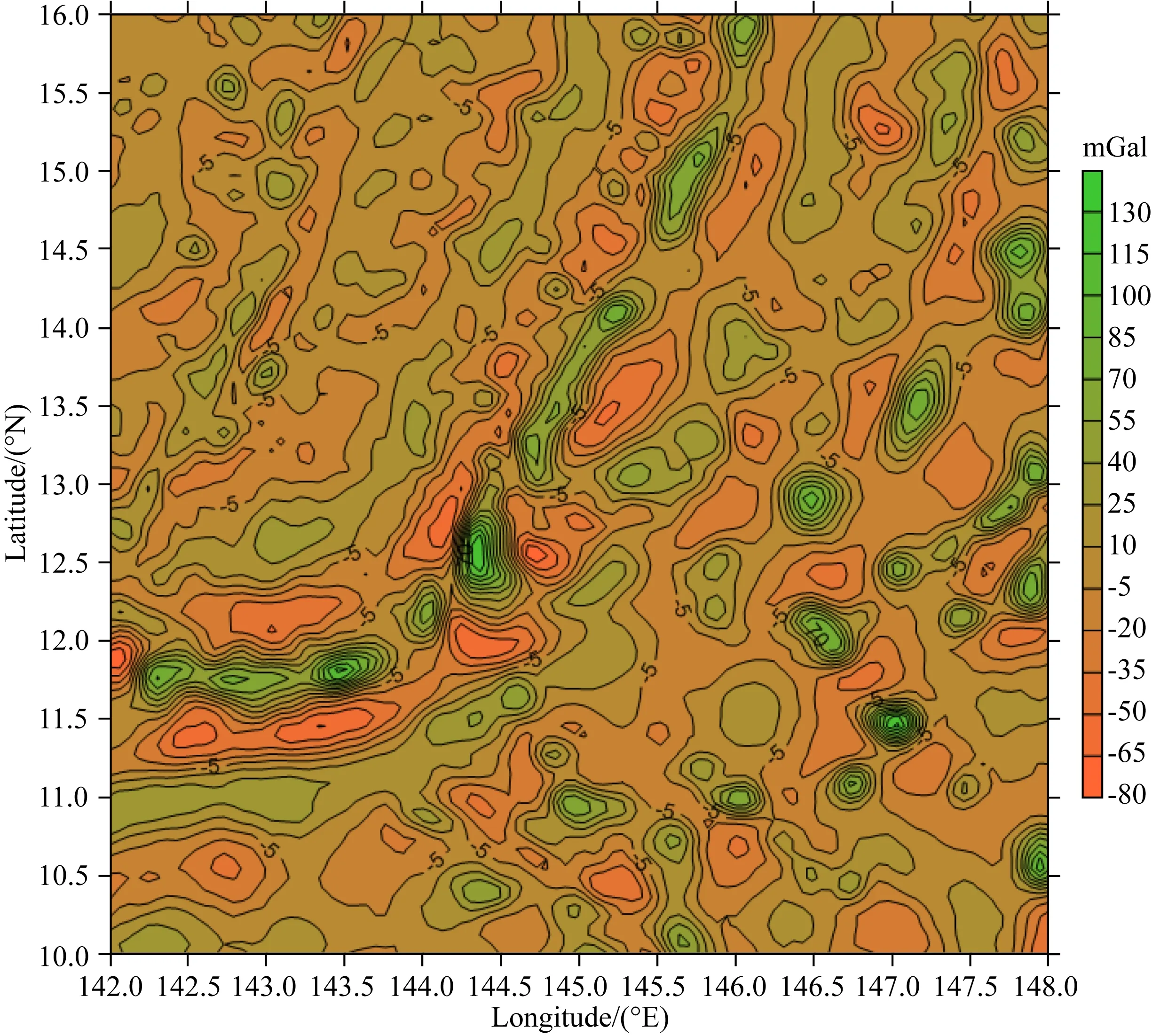
圖1 球面重力異常分布Fig.1 The gravity anomalies on the sphere

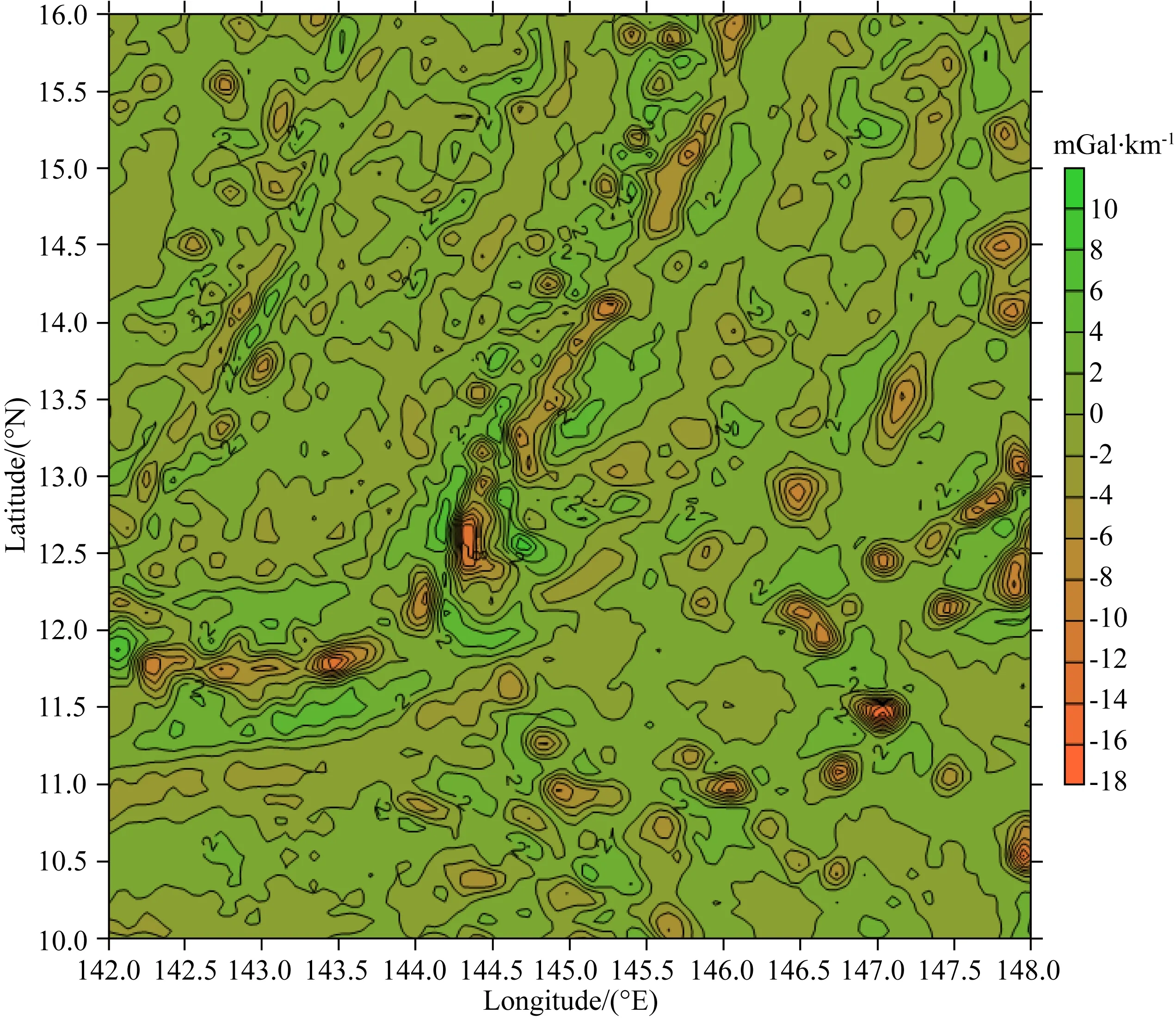
圖2 球面重力異常一階徑向偏導數分布Fig.2 The first order radial partial derivatives of the gravity anomaly on the sphere

在前述試驗基礎上，我們進一步采用同一高度面上的1′×1′網格重力異常“真值”Δgti作為觀測量，同時使用前述4種地面重力異常垂向梯度（Δg′Rp）改化模型，對相對應7個高度面上的1′×1′網格重力異常一階偏導數進行數值計算檢驗和分析，其中，第1模型是指直接對式（1）求徑向偏導數并令r=R作為基礎計算模型，且對全球積分域作了分區處理，但在實施近區計算時，扣除掉與計算點重合的1′×1′數據塊，以避免出現奇異積分；第2模型對應于公式（31）；第3模型對應于公式（36）；第4模型對應于公式（38）.將4種改化模型的計算值分別與相對應高度面的理論“真值”Δg′ti作比較，可獲得不同改化模型的精度評估信息，具體比對結果列于表4.

首先，從表2互比結果可以看出，我們對地球外部重力異常垂向梯度積分模型所作的分階段改化處理，取得了符合預期的解算效果.第1模型的誤差看似主要源于直接扣除了計算點所在數據塊的影響，實質上是由于該積分模型在邊界面存在不連續性所致.對比表2和表1結果可以看出，第1模型在1 km以下超低空高度段的誤差量值遠遠超過了垂向梯度自身大小，顯然，這不是忽略計算點所在數據塊影響所能引起的量值，而是第1模型原始計算式（直接對式（1）求徑向偏導數得到）在邊界面存在比較顯著的類似于質面和質體位那樣的數值跳躍所致，這是由地球重力位在邊界面存在不連續特性所決定的（Heiskanen and Moritz,1967）.這個結果說明，重力異常垂向梯度原始計算模型在超低空高度段是失效的，只有在5 km以上計算高度才是可用的.第2模型從理論上消除了第1模型的積分奇異性和數值不連續性影響，計算精度得到顯著提升，其相對檢核精度（指互差均方根/垂向梯度自身）都控制在20%以內，但由于該模型的改化過程存在不可忽略的理論缺陷，在10 km以上高度，該模型的計算精度反而不及第1模型.第3模型從理論上彌補了第2模型的缺陷，使得該模型的計算精度得到進一步改善，在超低空高度段，該模型的相對計算精度不低于7%，在1 km以上高度段，相對精度優于3%.這個結果說明，我們對第2模型所作的修正和補償處理是正確且有效的.第4模型是在第3模型基礎上，增加了計算點所在數據塊重力變化特征對計算參量的影響，表2結果顯示，相比第3模型，第4模型計算精度在300 m以下超低空高度段又得到一定程度的提升，在零高度面，其相對計算精度從6.7%提升到4.0%，提升幅度超過40%，充分體現了該模型的改化效果.可以預見，當采用的數據網格間距加大（比如從1′×1′增大到2′×2′）且計算點周圍的重力異常場變化更為劇烈時，第4模型的改化效果會更加顯現.

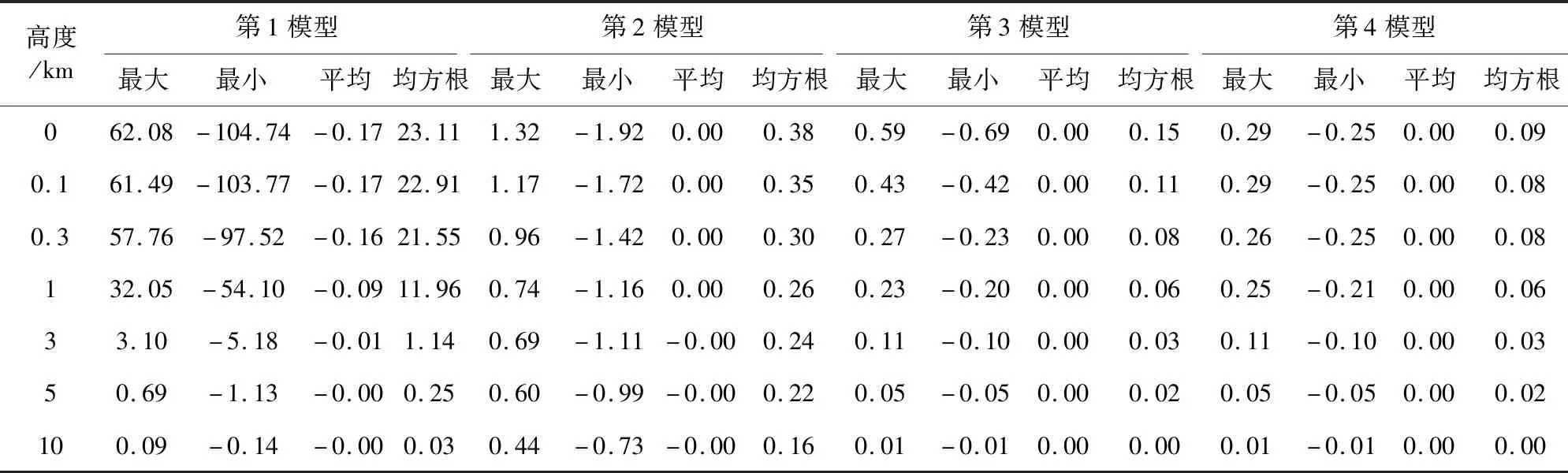
表2 由不同外部改化模型計算得到的7個高度面重力異常一階導數與“真值”比較（單位：mGal·km-1）Table 2 Comparisons between the first order radial partial derivatives of gravity anomalies,obtained by different modified models outside the earth,and the “true values”on 7 altitude surfaces （unit:mGal·km-1）

表3 模型誤差補償量Δg′rp（σ-σ0）計算結果統計（單位：mGal·km-1）Table 3 Statistics of the computational results of model error compensation Δg′rp（σ-σ0） （unit:mGal·km-1）

表4 由不同地面改化模型計算得到的7個高度面重力異常一階導數與“真值”比較（單位：mGal·km-1）Table 4 Comparisons between the first order radial partial derivatives of gravity anomalies,obtained by different modified models on the surface,and the “true values”on 7 altitude surfaces （unit:mGal·km-1）

由表3計算結果可進一步看出，盡管第3模型對第2模型的補償量均隨參考場階數N、積分半徑ψ0和計算高度h的增大而減小，但當參考場階數取N=360時，即使積分半徑增大到ψ0=5°，7個高度面的誤差補償量均方根值仍然接近甚至超過垂向梯度自身大小的10%.這樣的結果再次說明，對于高精度要求的地球重力場逼近計算，對重力異常垂向梯度傳統積分模型進行精細改化和校正是非常必要的.

對比表4和表2計算結果可以看出，在相同的數據分辨率和精度保障條件下，利用某一高度面的重力異常觀測數據計算該高度面外部的重力異常垂向梯度，其精度都要比利用本高度面觀測數據計算本高度面的垂向梯度精度高.這個結果顯然跟重力異常垂向梯度積分計算模型誤差隨計算高度升高而衰減有關.相比較而言，因第1模型在邊界面存在較大的數值跳躍問題，故利用該模型和本高度面觀測數據計算本高度面垂向梯度的結果偏離理論“真值”的幅度最大，完全失去了其使用價值.第2至第4模型兩種方式計算得到的垂向梯度精度差異相對較小，但在條件允許情況下，仍應優先采用前一種脫離邊界面的方式進行垂向梯度計算.

2.3 改化模型向下延拓應用效果分析

為了考察垂向梯度計算模型改化誤差對重力異常向下延拓解算結果的影響，這里特別設計如下試驗流程：

步驟一：使用地球外部6個高度面上的重力異常一階徑向偏導數理論“真值”Δg′ti，依據公式（39）將對應于6個高度面上的重力異常Δgti向下延拓到零高度面，分別將各個高度面的延拓計算值與零高度面的理論“真值”Δgt0作比較，計算互差統計結果.

步驟二：將式（39）中的垂向梯度替換為與表2統計結果相對應的外部重力異常一階徑向偏導數（Δg′rp）4種改化模型的計算結果，重復步驟一的試驗.

步驟三：將式（39）中的垂向梯度替換為與表4統計結果相對應的地面重力異常一階徑向偏導數（Δg′Rp）4種改化模型的計算結果，重復步驟一的試驗.

前述三步驟計算統計結果列于表5，為節省篇幅，表中只列出其中的對比互差均方根值（RMS）.

從表5統計結果可以看出，垂向梯度計算模型誤差直接影響重力異常向下延拓的解算精度，對積

表5 不同改化模型計算一階導數用于重力異常向下延拓與“真值”比較（互差均方根值）（單位：mGal）

分計算模型的修正和改化效果已經在向下延拓的解算結果中得到充分體現.不難看出，使用球面外部第3和第4模型計算得到的垂向梯度（Δg′rp）實施重力異常向下延拓解算的效果，已經完全等同于使用垂向梯度理論“真值”（Δg′ti）獲得的解算效果，兩個模型計算值與使用“真值”計算結果的差異不超過0.1 mGal；而使用第1模型時，兩者的差異超過10 mGal；使用第2模型時，兩者的差異也超過1 mGal,這些結果再次驗證了嚴密改化模型的有效性.需要指出的是，重力異常向下延拓的解算精度除了與垂向梯度計算精度水平密切相關外，還取決于向下延拓模型自身的完備性、延拓高度大小及計算區域重力場變化的劇烈程度.就本試驗而言，由表5可以看出，將第1模型排除在外，使用只顧及到一階項的向下延拓模型即公式（39）進行重力異常歸算，要想得到優于1 mGal的解算精度，必須將向下延拓高度控制在1 km以內，否則，需要將向下延拓模型拓展到更高階次（黃謨濤等,2018）.這方面的內容已經超出本文的研究范圍，這里不再做深入討論.

3 結論

將全球積分模型改化為局域模型是實現重力異常垂向梯度精密計算的前提條件.本文分析研究了重力異常垂向梯度全球積分計算模型的技術特點和適用條件，指出了開展積分模型精密改化的必要性和可行性.針對全球積分模型向局域積分轉換中遇到的積分奇異性和不連續性問題，綜合采用積分恒等式變換和移去恢復換算技術，同時依據實測數據保障條件，分別推出了計算地球外部及地面重力異常垂向梯度全球積分模型的分步改化公式，提出了補償傳統改化模型理論缺陷的修正公式.采用超高階地球位模型EGM2008作為模型比對標準重力異常場，同時選擇在重力異常場變化比較劇烈的馬里亞納海溝區塊開展數值計算試驗，分別對本文推出的重力異常垂向梯度兩類8種分步改化模型的計算精度及向下延拓應用效果進行了檢核分析和評估.試驗結果表明，采用最終的嚴密改化模型不僅可以有效消除原計算模型固有的積分奇異性和數值跳躍問題，又可顯著提高超低空重力異常垂向梯度的計算精度和穩定性，有效提升重力異常向下延拓的解算精度水平.因此，新的嚴密改化模型具有較高的推廣應用價值，可用于地球表面及外部重力場的高精度逼近計算.