基于改進粒子群算法的飛行器協(xié)同軌跡規(guī)劃

周宏宇 王小剛 單永志 趙亞麗 崔乃剛

現代防空反導體系已具備全天域、多層次、多維度防御能力;在此背景下,傳統(tǒng)彈道彈和巡航彈已無法滿足復雜對抗態(tài)勢下的作戰(zhàn)需求.因此人們開始研究具有多空域機動能力的臨近空間高超聲速滑翔飛行器.美國于2003 年便提出了HTV-2 (Hypersonic technology vehicle 2)[1-2]計劃,并于2017年完成了高超聲速滑翔試驗[3].俄羅斯于2015 年和2017 年分別完成了高超聲速飛行器“Yu-71”和“先鋒”的飛行試驗[4].日本于2019 年起加緊研制高速滑翔飛行器[5];同年,印度也完成了高超技術驗證機首飛[6].

基于出色的突防能力,多高超聲速飛行器協(xié)同作戰(zhàn)模式[7]同樣備受關注.但同時規(guī)劃多條滑翔段軌跡具有一定難度:1)約束多,如載荷、熱等過程約束以及位置、高度等終端約束;2)耦合強,如氣動-約束-軌跡-指標;3)干擾多、速度快、航程遠.綜上,在線規(guī)劃方法必須具備很強的場景適應性,同時還要精確控制各飛行器間的相對運動關系.

許多學者針對高超聲速飛行器滑翔段軌跡規(guī)劃問題展開了研究.孫長銀等[8]探討了高超聲速飛行器領域的新方法和新問題,提出了一種通用的大包絡飛行動力學模型;Liao等[9]基于有限時間非線性觀測器實現了滑翔段軌跡的在線規(guī)劃.在協(xié)同規(guī)劃方面,王芳等[10]提出了一種時間最優(yōu)導彈編隊方法,Vincent等[11]和Chen等[12]分別用遺傳算法和粒子群優(yōu)化(Particle swarm optimization,PSO)算法實現了無人機編隊控制,Xu等[13]提出了一種用于故障條件下多巡航彈協(xié)同控制的時變容錯算法.

現有方法有效解決了滑翔段軌跡設計問題,但協(xié)同規(guī)劃方面的研究多以巡航彈/無人機為研究對象.針對上述問題,從提高在線規(guī)劃效率出發(fā),本文提出一種自動滿足終端約束的滑翔段飛行剖面.推導滑翔段解析解,實現了飛行剖面的快速重構.提出一種基于慣性權重智能選擇的改進PSO 算法,用于完成在線協(xié)同規(guī)劃.最后通過數學仿真驗證了方法的正確性和有效性.

1 飛行器協(xié)同軌跡規(guī)劃問題建模

1.1 滑翔段運動數學模型

高超聲速飛行器滑翔段運動方程為

式中,cend為終端約束,cpath為過程約束.下標“f”表示實際終端狀態(tài),下標“ter”表示期望終端狀態(tài).下標“max”表示該過程變量允許的最大值,Nm為法向過載的絕對值.

1.2 多飛行器協(xié)同軌跡規(guī)劃模型

2 滑翔段飛行剖面設計

設飛行高度為剩余航程的函數為

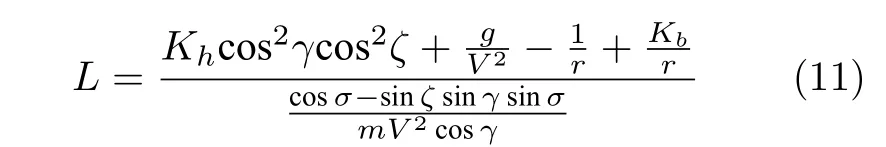
式中,Kb=2 sinγcosγsinψtan?sinζ.

設n=5,則確定F(RL)需建立6 個方程.由于初始和終端高度已知,由式(8)可得

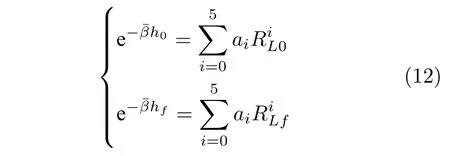
式中,下標“0”表示滑翔段初始運動狀態(tài).

自1978年改革開放以來，中國公共圖書館事業(yè)展開了新時期波瀾壯闊的歷史發(fā)展進程。在數十年中國公共圖書館事業(yè)精彩紛呈、百舸爭流的服務品牌實踐中，如何認知服務品牌的文化內涵、如何理解服務品牌所體現的時代邏輯、如何總結具有中國特色的服務品牌的創(chuàng)意與生動實踐、如何揭示服務品牌內在的規(guī)律與方法、如何直面服務品牌建設中尚存在的問題并在新時代推進服務品牌進一步轉型升級并實現與時俱進的再出發(fā)，這些都是我們應當思考并予以回答的問題。

由于初始和終端飛行路徑角已知,認為cosζ ≈1,由式(9)可得

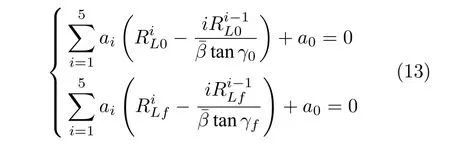
設h1,h2分別為剩余航程2/3 處(記為RL1)和1/3 處(記為RL2)的高度值,由式(8)可得:

式中,ζmax為給定正數.

3 滑翔段高精度解析解推導

滑翔段高度的解析解即式(8).考慮到滑翔段中航向偏差ζ和飛行路徑角γ較小,由式(1)和式(9)可得飛行路徑角的解析解為

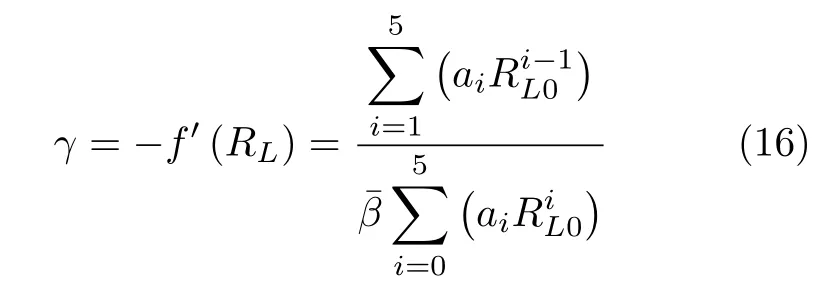
考慮到滑翔段中阻力通常遠大于引力沿速度方向的分量,根據式(1)可得

4 滑翔段軌跡協(xié)同規(guī)劃算法

4.1 基本PSO 算法

式(29)避免了對粒子速度進行初始化及更新,算法結構更簡潔,利于提高計算效率.

調整權重是控制粒子尋優(yōu)過程的常用方法.借助強化學習方法,通過快速智能選擇慣性權重實現用較少的粒子數和迭代次數找出滿足協(xié)同規(guī)劃參數

4.2 最優(yōu)權重在線生成方法

設慣性權重為進化代數的分段函數如下:

4.3 在線協(xié)同軌跡規(guī)劃方法

設從當前位置到起點的航程為Rcov,更新周期為 ΔRcov.如圖1 所示,在線協(xié)同規(guī)劃具體步驟如下:

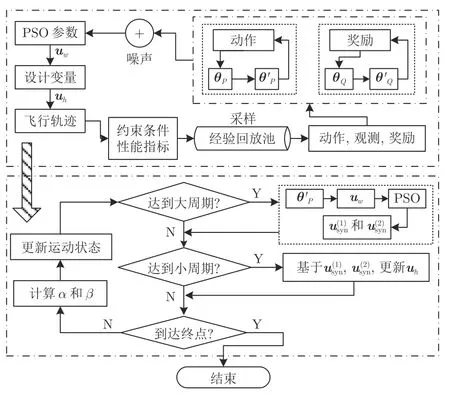
圖1 在線規(guī)劃算法流程圖Fig.1 The flowchart of the planning algorithm

步驟 1.協(xié)同飛行剖面重構

步驟 2.個體飛行剖面重構

a)計算RL1,RL2及其對應高度值h1,h2;

b)求解系數a0～a5,更新飛行剖面.

步驟 3.計算攻角和傾側角,更新運動狀態(tài).

步驟 4.計算航程Rcov; 根據Rcov,每5 個周期(5ΔRcov)執(zhí)行一次協(xié)同剖面重構,每1 個周期(ΔRcov)執(zhí)行一次個體剖面重構;未到達更新周期時,各飛行器只執(zhí)行步驟3.

循環(huán)執(zhí)行步驟 1～4,直至飛行器到達目標點上空.步驟2 用于控制終端高度和飛行路徑角,但未考慮過程約束;步驟1 既要保證時間協(xié)同,又要通過優(yōu)化求解來滿足過程約束,同時還負責修正解析解與實際值間的偏差.

5 仿真分析

參考文獻[16-17],設滑翔段過程約束為qmax=60 kPa,Nmax=3.0,αmax=25°,σmax=50°.考慮對4架總體參數不同的高超聲速飛行器進行協(xié)同規(guī)劃;參考X-33[18],設其特征面積分別為2.0 m2,1.6 m2,1.3 m2和1.0 m2,質量分別為950 kg,900 kg,850 kg 和800 kg.

設PSO 算法的最大進化代數為15,粒子數為20,約束條件用罰函數法[19]處理,當Jsyn＜ 1或?=?max時停止進化.

仿真條件見表1,初始航向角由式(5)求出,故初始航向偏差為零.取 ΔRcov=30 km,仿真結果見圖2～5.仿真結果表明,各軌跡均能滿足終端約束條件和過程約束條件,且攻角和傾側角曲線十分平滑.各飛行器到達目標的時刻分別為735 s,734 s,734 s 和734 s.

表1 初始狀態(tài)和終端約束Table 1 The initial states and the terminal constraints

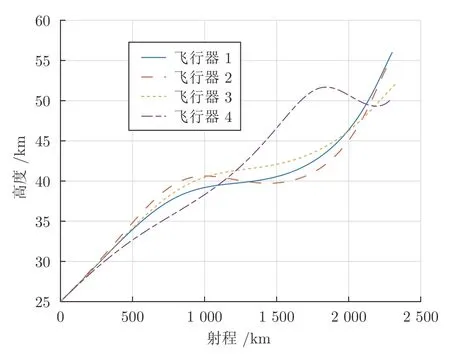
圖2 滑翔段飛行剖面Fig.2 Flight profiles of different vehicles

若不進行協(xié)同規(guī)劃,各飛行剖面設計參數均取h1=42 km,h2=38 km,則各飛行器的到達時刻為694 s,703 s,733 s 和744 s,說明協(xié)同規(guī)劃方法正確有效.

表2 基本PSO 和改進PSO 計算效率對比Table 2 Comparison of the computation efficiency

最后,為驗證協(xié)同規(guī)劃方法的抗干擾性,設置服從高斯分布的干擾因素(見表3),并進行500 次蒙特卡洛打靶仿真.500 次仿真中,最晚與最早到達時刻之差的最大值為5.37 s,平均值為1.57 s,說明算法能夠在干擾因素的影響下完成在線協(xié)同規(guī)劃.

表3 滑翔段干擾因素設置Table 3 Disturbances in the glide phase

以飛行器1 為例,給出打靶仿真結果如圖6 和圖7 所示.結果表明,各種約束條件依然能夠得到滿足.在高度和飛行路徑角的解析解推導過程中未用到近似假設條件,因此可忽略它們和真實值間的誤差.對于速度和剩余時間的解析解,相應誤差會隨著時間而減小,并且剩余時間是根據實時運動狀態(tài)估計的,因此不存在累計誤差.

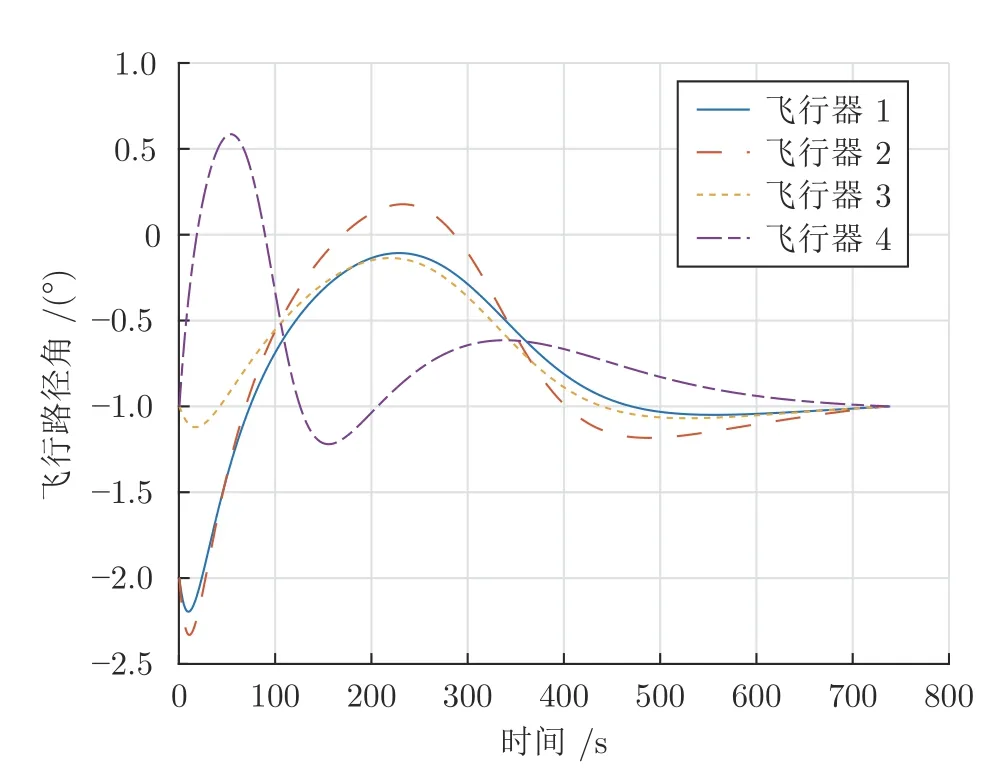
圖3 飛行路徑角隨時間變化情況Fig.3 Time histories of the flight path angle

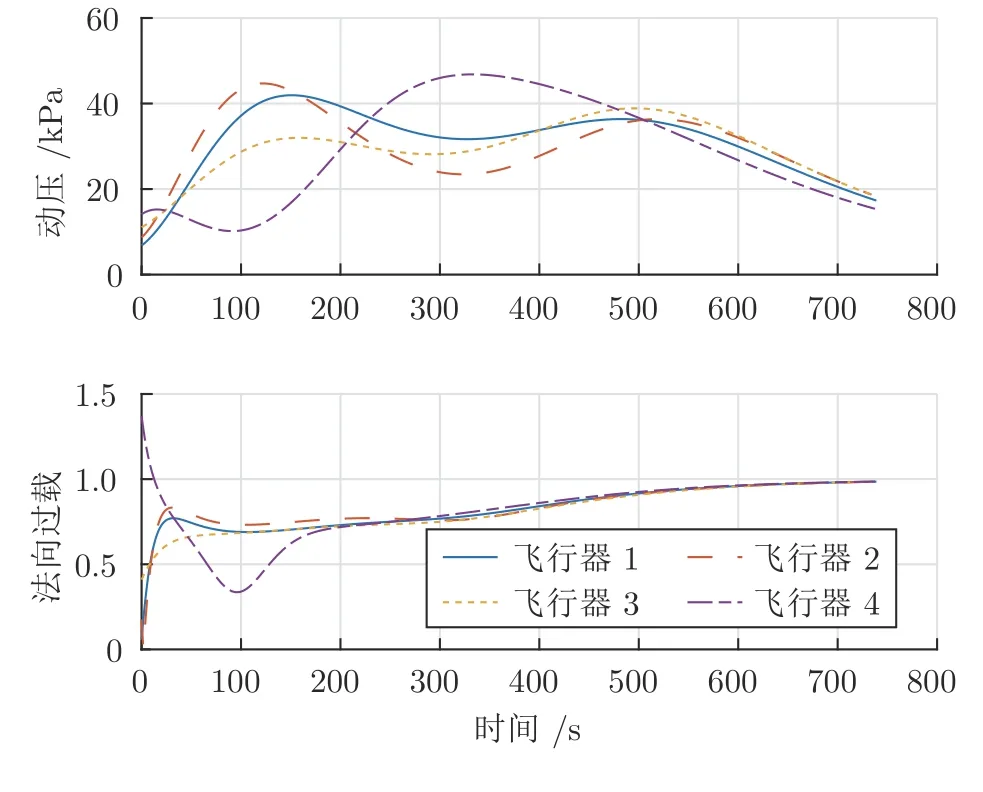
圖4 過程約束隨時間變化情況Fig.4 Time histories of the path constraints

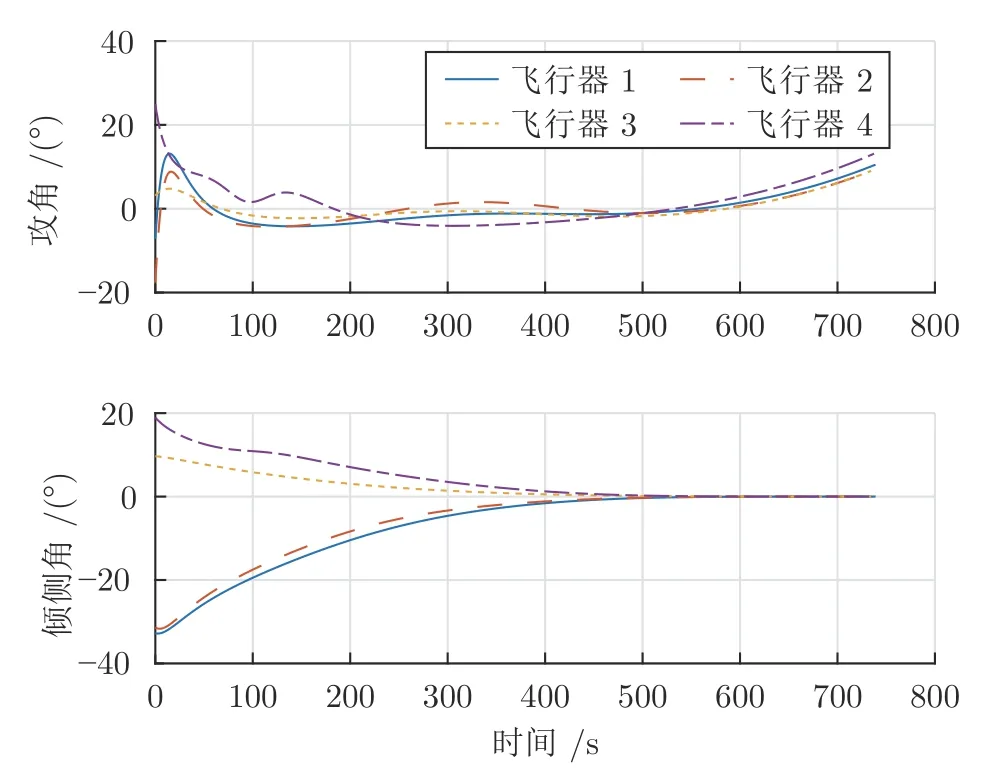
圖5 攻角和傾側角隨時間變化情況Fig.5 Histories of angle-of-attack and the bank angle

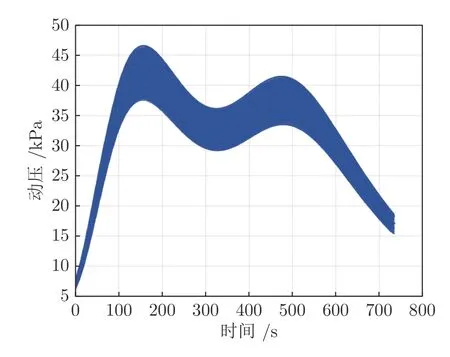
圖7 動壓隨時間變化情況(飛行器1)Fig.7 Histories of the dynamic pressure (Vehicle 1)

6 結束語

本文建立了多高超聲速滑翔飛行器協(xié)同規(guī)劃問題數學模型.提出了一種新的滑翔飛行剖面,實現了終端約束的自動滿足,并推導了滑翔段解析運動方程.提出基于強化學習方法的改進PSO 算法,提高了在線協(xié)同規(guī)劃效率.仿真結果表明,在初始狀態(tài)和總體參數各異的情況下,多彈時間協(xié)同偏差不超過2 s,并且能夠克服干擾因素的影響.