課程視域下的數學單元作業重構
——以指數函數、對數函數的圖象與性質復習課為例
韋慶賀
(江蘇省連云港市厲莊高級中學 222121)
1 引言
《學記》中說“時教必有正業,退息必有居學”,其中“居學”指課外作業,作業是達到“學以致用”和“以用促學”的重要手段.在教學過程中,為保證學生掌握知識的持久性和提升知識運用的靈活性,很多教師無力采取其他途徑,只有通過大量、重復的作業訓練,讓學生收集各種題型,以緩解學生在考試過程中面對新題型而產生的陌生感.隨著課程改革的進一步深化,如何利用作業提升教學質量和促進學生發展是一線教師亟待解決的問題.2019年國務院辦公廳印發了《關于新時代推進普通高中育人方式改革的指導意見》,提出提高作業設計質量,精心設計基礎性作業,適當增加探究性、實踐性、綜合性作業.作業設計要從學習活動整體考慮,系統、科學、合理設計不同層次的作業,引導學生自覺預習、及時整理和鞏固所學知識,養成良好的學習習慣.
2 單元作業有關概述
單元作業是為某個教學單元所設計的所有作業的總和.合理的單元作業應具有整體性、結構化和進階性的特點.單元作業可以增強同一單元不同課時作業之間的結構性和遞進性,減少一些僅僅針對低水平目標、反復操練性質的作業,進而留出時間增加發展高階思維、關鍵能力的作業比例,有助于發展學生的學科核心素養.
3 單元作業重構的教學實踐
根據課堂內容設計單元作業,本節課內容 為高三復習課:指數函數、對數函數的圖象與性質.
3.1 教學目標
(1)理解指數函數、對數函數的圖象和性質;
(2)能夠利用指數函數、對數函數的圖象和性質解決比較大小,會用研究函數性質的一般方法研究簡單的復合函數性質;
(3)解決簡單的含參復合函數、抽象函數不等式恒成立及存在性、函數零點等問題,體會從特殊到一般、數形結合、函數與方程等數學思想方法,發展學生數學運算、直觀想象、邏輯推理等數學核心素養.
3.2 教學重點和難點
本節課教學重點和教學難點主要體現于兩個層面:一是掌握指數函數、對數函數的圖象與性質,會應用函數性質解決簡單問題;二是解決不等式恒成立、存在性等問題的常用方法,會運用數形結合、函數與方程等思想方法解決問題.
3.3 教學過程
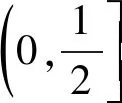
設計意圖此題入口寬,回顧指數函數、對數函數的圖象和性質,回顧解決不等式存在性問題及恒成立問題的常用方法,激活學生思維.
例題已知函數f(x)=ax+bx,其中a>0且a≠1,b>0且b≠1.
(1)請寫出一組數對(a,b),使函數f(x)為偶函數.
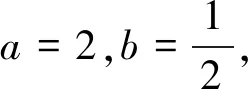
設計意圖第(1)問以兩個指數函數“疊加”形式呈現,給學生一個相對陌生的情境,并用“例題”的形式給出,是學生相對陌生的設問情境,激發其探究欲望,幫助回顧研究函數性質的基本方法.第(2)問以“結構不良”的形式設問,是新高考中的常見題型,不同的學生根據自身認知結構選擇條件嘗試解決,掌握解決復合函數方程根的問題、不等式恒成立問題、不等式存在性問題的常用方法與基本數學思想.
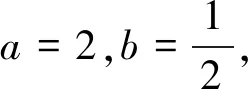
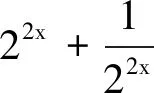
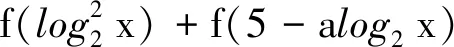
設計意圖將研究對象f(x)=ax+bx為偶函數改為研究f(x)=ax-bx為奇函數,結構形式上的相似及研究方法的相似,能較好地保持學生思維的連續性,使其思維處在高階狀態.但此變式并沒有給出具體的a,b的值(這也是此題的另一個難點),這需要學生調動研究抽象函數不等式問題的常用方法——轉化為“作用對象”大小關系問題.滲透類比思想、轉化與化歸思想,培養學生的邏輯推理、數學抽象等數學核心素養.
3.4 課堂小結
(1)指數函數、對數函數的圖象與性質;
(2)利用函數性質解決相關方程有根(或函數存在零點)、不等式有解或恒成立問題的方法與思想;
(3)解決函數問題,特別要關注數形結合、化歸與轉化、分類討論思想的應用.
4 單元作業重構中的幾個原則
4.1 合理設計基礎性作業

A.a C.c 題目來源及意圖作業1和作業2來源于人教A版《普通高中教科書高中·數學(必修第一冊)》復習參考題4,這兩道題旨在幫助學生回憶指數函數、對數函數的圖象和性質,并利用單調性進行比較大小、求值域等,體現作業的基礎性原則,對應教學目標(1). 教材是課程實施的重要載體,是教師設計作業的重要依據,明確教材中單元學習的目的和任務,并以此為標準設計整個單元的作業體系,才能確保作業設計不超綱、不走樣. 4.2 科學設計鞏固性作業 作業3:設函數f(x)=ln|2x+1|- ln|2x-1|,則f(x)( ). 2.2.4 重復性試驗 取同批浸膏粉末1 g,精密稱定,按“2.2.1”項下方法制備供試品溶液,平行試驗6份,測定峰面積,計算葛根素的含量。結果葛根素的平均含量為3.81 mg∕g,RSD值為0.40%,表明該方法重復性良好。 作業4:已知函數f(x)=2x+x,g(x)= log2x+x,h(x)=x3+x的零點分別為a,b,c,則a,b,c的大小順序是. 題目來源及意圖作業3來源于教輔精選,考查復合函數性質的一般研究方法.作業4來源于人教A版《普通高中教科書高中·數學(必修第一冊)》復習參考題4,考查函數與方程、數形結合的思想方法,這兩題體現作業的鞏固性原則,對應教學目標(2). A.f(x)為奇函數,g(x)為偶函數 D.函數f(x)與g(x)既無最小值,也無最大值 A.函數f(x)為偶函數 B.當a>1時,函數在f(x)在(0,+∞)上為減函數 題目來源及意圖作業5和作業6來源于教輔精選,考查研究復合函數性質的一般方法、數形結合思想等,與課堂例題相匹配,體現作業的鞏固性原則,對應教學目標(2)、(3). 4.3 適度設計拓展性作業 題目來源及意圖作業7為教輔改編題.本節課課堂上沒有出現“迭代函數”的相關例題及處理方法,但本題是一個利用數形結合解決問題的典型問題.設計在作業中,可以給部分優生一個自主探索發現的機會,并在此過程中進一步感悟數形結合思想,體現作業的拓展性原則,對應教學目標(3). 4.4 優化設計綜合性作業 作業8:設函數f(x)=log2(4x+a·2x-1),x∈[0,1]. (1)若a=1,求方程f(x)+x=0的根; (2)若方程f(x)+x=0在[0,1]上無實數根,求實數a的取值范圍. 題目來源及意圖作業8為教輔改編題,此題考查指對數運算、指對數函數的性質、恒成立問題、方程根的存在性問題等.問題分析和解決過程,體現了作業設計中注重方法指導、思維過程的表達與交流等功能,對應教學目標(3). 4.5 創新設計新情境作業 作業9:對于定義在[p,q]上的函數m(x),設x0=p,xn=q,用任意的xi(i=1,2,…,n-1)將[p,q]劃分成n個小區間,其中xi-1 |m(x0)-m(x1)|+|m(x1)-m(x2)|+…+ |m(xn-1)-m(xn)|≤M 恒成立,則稱函數m(x)為在[p,q]上的有界變差函數. (1)證明函數f(x)=2x+2-x是在[0,2]上的有界變差函數,并求出M的最小值; (2)寫出一個f(x)在[p,q]上是有界變差函數的充分條件,使上述結論成為其特例(不要求證明). 題目來源及意圖作業9改編自2021年上海市期末考題,是一個“新定義”情境下的問題.首先,要熟悉函數f(x)=2x+2-x的性質(這是對課堂內容的回顧),其次需要從題干信息中分析出M的求法,考查學生數學抽象、數學運算、邏輯推理等核心素養,對應教學目標(3). 在強調作業“減負增效”的背景下,教師應當轉變觀念,科學評估作業質與量的關系.數學單元作業重構應貫徹全面育人理念,關注學生核心素養的養成,關注學生個體間的差異,關注各學科各階段作業量,關注五育教育融合,助力每位學生全面發展.