基于準粒子模型的原生磁星研究*

王誼農 初鵬程 姜瑤瑤 龐曉迪 王圣博 李培新

(青島理工大學理學院,青島 266033)

研究了奇異夸克物質在零溫、有限溫度、強磁場下基于準粒子模型的熱力學性質.結果說明夸克物質的對稱能會隨著準粒子模型的耦合常數增加而增加,對稱能越大夸克物質的物態方程就越硬;結果還表明溫度場與磁場對奇異夸克物質的每核子能量、每核子自由能、各向異性壓強都有較大影響.通過對原生磁星的計算,發現原生磁星的最大質量和核心溫度不僅受到原生星演化過程中的加熱過程影響,還與磁星內部磁場強度與磁場方向的分布密切相關.隨后考慮了磁星內部徑向、橫向磁場混合的情況,發現磁星最大質量會隨著磁場方向與徑向的夾角變化.本文所做工作對于理解有限溫度、強磁場下奇異夸克物質的同位旋效應和熱力學性質以及致密星體物理中的原生磁星的性質具有一定的推進作用,為接下來尋找磁星內部的真實磁場分布提供了前期理論基礎.

1 引言

研究強相互作用物質的熱力學性質是核物理、宇宙學、粒子物理等前沿的重要基礎問題之一[1–4],其物態方程的求解對于理解核反應與核結構、致密星體物理、早期宇宙的物質形態等前沿物理領域具有重要的作用.在地球實驗室,重離子碰撞實驗是探索強相互作用物質的重要手段,如相對論重離子碰撞實驗(RHIC)、大型強子碰撞實驗(LHC)等已經能夠揭示低密、高密、高溫的強相互作用物質的性質;在自然界中,中子星的相關實驗觀測結果則為人們探索高密、低溫的強相互作用物質提供另一種途徑.在致密星體工作中,星體內部奇異夸克物質能否出現是熱點問題—如果奇異夸克物質在中子星物質中占比增加,那么人們可以進一步研究由奇異夸克物質構成的(奇異)夸克星,而夸克星的存在可能性仍為現代核物理和天體物理的未解重要課題,不能夠被排除[5–11].構成夸克星的奇異夸克物質是由退禁閉的u,d,s 三味夸克以及輕子通過β平衡組成的[12–16],一般來說奇異夸克的加入會增加自由度,進而使得物態方程變軟,所以通常很難用合理的夸克模型來描述實驗觀測得到的大質量致密星體為夸克星.然而經過嘗試,科研工作者也可以通過考慮手擺增加袋常數、同位旋相關勢能或有效質量、有效質量密度相關等方法得到較大質量夸克星[17–26].在最近的實驗探測中,大質量脈沖星結果多次出現:2013 年觀測的PSR J0348+0432 脈沖星的質量為(2.01±0.04)M⊙[27],是當時精確探測的大質量脈沖星之一;2018 年觀測的脈沖星PSR J 2215+5135的質量更大,達到了[28].在文獻[29]中,人們通過相對論引力時間延遲效應得到的脈沖星MSR J0740+6620的最大質量達到了(68.3% 置信度)、(95.4% 置信度).最新LIGO/Virgo 合作組觀測到的雙致密天體并合事件GW190814[30]的“次星”m2質量能達到 2.50M⊙?2.67M⊙(90%置信度).如此大質量的致密天體如果候選者是夸克星,會對奇異夸克物質的物態方程等熱力學性質有著更強的約束,對夸克物質的唯象模型也有了更高的要求.此外,對于大質量中子星的情況還存在著其他的解釋,比如其他的星體模型或者大質量中子星的質量可能與其伴星的質量和金屬豐度相關等[31].目前發現的大質量中子星幾乎都位于高質量 X 射線雙星雙星系統(HMXB)之中,這預示大質量中子星質量可能與雙星系統中的伴星質量、金屬豐度和對流超射系數正相關[32].

原生星通常認為發生在超新星爆發后,此時星體已經耗光了能源補給,可能會被引力壓縮而形成致密星體或者是黑洞,具體成因與坍縮的具體初始條件有關[33].對于從原生中子星到原生夸克星的相變,人們知之甚少,因為在星體燃燒過程中核子夸克相變的復雜性相對較高.之前的相關工作表明[10,34–40],奇異夸克星有可能來自中子星的并合,也可以用星體演化中的不同等熵階段去描述奇異夸克星的質量、半徑等性質.這對于解釋原生星的加熱、冷卻過程以及有限溫度下夸克星物質的熱力學性質具有非常重要的意義.

據估算,致密星體表面磁場B接近 1014G[41–43],內部可能會增加至 1018G[44]到1020G[45].如此巨大的內部磁場,會使得致密星體物質的空間旋轉對稱性破卻,壓強會各向異性[45–48].沿著磁場方向的壓強(縱向壓強)經過計算一般會小于垂直于磁場方向的壓強(橫向壓強).在描述磁星內部磁場強度分布的時候,人們通常采用密度相關磁場[49–54],所以如何去探索磁星內部磁場強度與方向分布對磁星物質的熱力學性質(尤其是物態方程)的影響是磁星研究的重點,對于核物理、天體物理具有非常重要的作用.如果考慮得更深入,在研究磁星的性質中考慮原生星的演化曲線上的不同的等熵階段,可以求解原生磁星的性質.原生磁星是一類轉動周期為毫秒量級的具有超強的磁場(B >1018G)、超高溫度(T >1010K)的原生致密星體,其與依靠磁場供能的可被觀測的“磁星候選體”(軟伽馬重復爆和反常X 射線脈沖星這兩類源可統一被稱為“磁星候選體”)有著一定的差異性,可以作為唯象的理論模型解釋快速射電暴以及伽馬射電暴的起源問題[55].較高的X-射線光度和頻繁的外爆是由磁星內部超強磁場的衰變提供能量來源及動力,由磁偶極輻射模型推導出的表面磁場可達到1013—1015G,內部磁場可能更高.時至今日,磁星模型已經發展到了相當的規模,為軟伽馬重復爆和反常X-射線脈沖星在高能段多樣性觀測現象提供了令人滿意的解釋[56–58].故磁星的性質與快速射電暴以及伽馬射電暴的研究密不可分,考慮到在不同等熵階段中溫度場會對磁星物質有非常大的影響,最終星體演化中的加熱、冷卻階段可能會影響到磁星的質量與半徑等相關性質,這是我們研究的重點內容.

本文安排如下:首先基于準粒子模型介紹零溫、有限溫度、強磁場下奇異夸克物質的熱力學量的推導,并給出奇異夸克物質需滿足的電中性、重子數守恒、β 平衡等條件;其次通過計算與畫圖,詳細討論零溫、有限溫度、強磁場下奇異夸克物質的熱力學性質;最后利用TOV 方程求解原生星與磁星的相關性質,并給出結論.

2 前期推導工作

2.1 準粒子模型理論推導

與常用的夸克物質的唯象模型(比如質量密度相關模型)不同,準粒子模型的提出不是建立在把夸克與夸克、夸克與介質之間的相互作用包含在重子數密度相關的 有效質量中[59–79],而是來自硬密環的單圈自能近似得到的色散關系的零動量極限結果,具體表達式如下[80–82]:

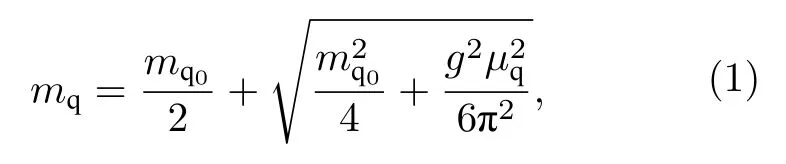
這里mq0是夸克的裸質量,設u,d,s 三味夸克的裸 質量分別為mu0=5.5 MeV,md0=5.5 MeV,ms0=95 MeV.μq代表著第i味夸克的化學勢,g是強相互作用的耦合常數,這里設為可調參數.需注意的是,g作為強相互作用耦合常數,原則上需要隨著溫度場與磁場進行跑動,這對于更清楚地理解溫度場與強磁場下的工作更有意義,由于計算上與定義上存在一定的困難,我們將在之后的工作中對強耦合常數進行更加深入的討論.

于是奇異夸克物質的總熱力學勢密度可以寫為

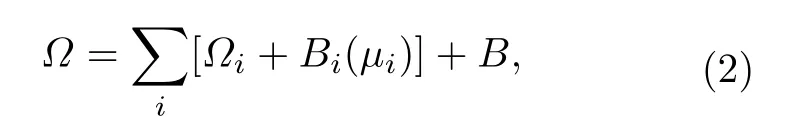
這里Bi(μi)是準粒子模型中有效質量項化學勢相關所產生的附加項,B是提供夸克禁閉的可調參數,?i則代表奇異夸克物質中的每味夸克、輕子對應的熱力學勢密度,在有限溫度與強磁場情況下其表達式可寫為

式中pz是z方向動量,Bi(μi)的積分形式可寫為

這里需要注意的是,Bi這個參數產生的原因是由于準粒子模型中夸克的有效質量與化學勢相關所自洽求解得到的附加項,正是由于此項在熱力學勢密度中的參與,才使得最終基于準粒子模型的推導滿足不依賴于參數空間的熱力學自洽.

夸克與輕子的粒子數密度的表達式為

自由能密度F可以通過熱力學關系求出,注意最后一項來自于磁場:

由于外加強磁場,磁場對能量的貢獻B2/2 需要考慮.致密星體內部也存在著強磁場,其表面的磁場B可能高達 1014G[41–43];而星體內部的磁場則可能會增加到 1018G[44].在之前的磁場工作中[45],夸克星核心的磁場甚至可能高達 1020G.如此強的磁場會破壞空間旋轉對稱性(O(3)),進而使得奇異夸克物質的壓強發生劈裂[45–48].劈裂后的各向異性壓強可以定義為平行于磁場方向的縱向壓強P∥以及垂直于磁場方向的橫向壓強P⊥,相應的表達式可以寫為[45]

這里M是系統的磁化率,具體表達式為

通過(10)式可見,縱向壓強在強磁場情況下比橫向壓強的取值低,而且縱向壓強P//可以滿足Hugenholtz-Van Hove 定理,體現了熱力學自洽性.對于能量密度εi,其表達式可以寫為

有限溫度情況下的奇異夸克物質的熵的表達式可寫為

接下來可以通過求解有限溫度、強磁場下奇異夸克物質的熱力學性質進而求解夸克星的性質.

2.2 奇異夸克物質

奇異夸克物質是由u,d,s 三味夸克以及輕子(e,μ,νl等)通過電中性條件構成.在確定了重子數密度之后,各種粒子需要滿足β 平衡條件:

對于有限溫度情況,需要考慮中微子,故β 平衡條件為

奇異夸克物質的電中性條件為

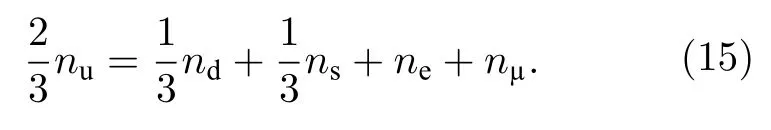
需要注意的是零溫情況下μ子的產生需要電子的化學勢達到μ子的質量才可發生,對于s 夸克,由于低密度處d 夸克的化學勢較低,可能會在重子數密度較低時組分為零.

接下來采用準粒子模型分別計算不同情況下的奇異夸克物質的熱力學性質.

3 奇異夸克物質性質計算結果

在核物理學家的普遍認知中,奇異夸克物質有可能是最穩定的物質形態,其滿足所謂的絕對穩定條件[9],也就是說零溫情況下的奇異夸克物質的每核子能量應該低于自然界最穩定核素M(56Fe)的每核子能量930 MeV;而在實驗室與自然界中,從正常核物質到只有u,d 兩味夸克構成的純u-d夸克物質的相變并沒有觀測到,故絕對穩定條件還要求純u-d 夸克物質的每核子能量最低點要高于930 MeV.考慮絕對穩定條件會進一步約束唯象夸克模型的參數空間,對唯象夸克模型提出了挑戰.由于奇異夸克的加入會使得夸克物質物態方程變軟,可能會很難描述大質量致密星體.近年來人們通常利用引入有效袋常數、增加矢量道耦合常數等方法,這些方法可以描述較大質量的夸克星,其中的考慮夸克物質的同位旋性質、通過調節夸克物質對稱能來給出較硬的物態方程的方法得到了越來越多的關注[17–26].和核物質的對稱能定義相似,夸克物質的對稱能是將夸克物質的每核子能量對不對稱度δ進行泰勒展開,二階項系數Esym即為夸克物質對稱能,相應結果如下:

其中,E0(nB,ns)=E(nB,δ=0,ns)是三味 u-d-s 夸克物質中考慮u 夸克和d 夸克組分相等的情況(通常稱之為對稱夸克物質),夸克物質的對稱能Esym(nB,ns)可以寫為

圖1 描述的是基于準粒子模型的夸克物質對稱能基于不同的參數隨重子數密度的變化.這里選取四套參數,分別是g-2(g=2,B1/4=141 MeV),g-3(g=3, B1/4=136 MeV),g-4(g=4, B1/4=131 MeV)和g-5(g=5, B1/4=120 MeV).在我們之前的工作[83–86]中,利用此四套參數 計算了不同情況下的夸克星,其中在零溫情況下分別描述了PSR J0348+0432(質量為(2.01±0.04)M⊙[27]),MSR J0740+6620(質量為),PSR J2215+5135(質量為[28]),及GW190814引力波并合事件中的可能為中子星的致密天體(質量為2.50M⊙—2.67M⊙[30])為夸克星,所以選取這四套參數研究基于準粒子模型下的零溫夸克物質對稱能.從圖1 可以看出,對于所有的參數情況,夸克物質的對稱能都會隨著重子數密度的增加而增加.取值越大的對稱能同位旋效應越強,通常可使得夸克物質的物態方程變硬,進而能夠描述更大質量的夸克星.對比[83]夸克星最大質量結果,可直接給出基于準粒子模型較高的對稱能能夠支持大質量致密星體的結論.

圖1 基于不同參數的夸克物質對稱能Fig.1.Quark matter symmetry energy with different parameter sets.

圖2 給出了零溫、有限溫度、強磁場下奇異夸克物質的每核子自由能/能量、壓強隨重子數密度的變化,這里選擇了g-2 這套參數.圖2 中對于有限溫度情況選取T=50 MeV、磁場情況選取B=2×1018G,經過計算在溫度大于50 MeV的時候溫度場效應特別明顯;磁場在高于B=2×1018G時,零溫磁場的朗道能級上限變化所引起的“振蕩”以及壓強劈裂會更清楚.從圖2 可以發現,在零溫情況,奇異夸克物質的每核子能量最低點低于 930 MeV,滿足了絕對穩定條件;其次在有限溫度情況時,奇異夸克物質的每核子自由能與每核子能量的取值不再相等(有限溫度情況下,自由能與能量表達式中的 T S0),故可以發現,考慮有限溫度時每核子自由能/能量會隨著溫度的增加而降低/升高,出現了明顯的溫度相關的劈裂.在考慮零溫有磁場的情況時,發現當磁場提升至B=2×1018G時,壓強出現了明顯的各向異性,平行于磁場方向的縱向壓強P//與垂直于磁場方向的橫向壓強P⊥之間出現了隨磁場增加的劈裂.零溫情況強磁場下,每核子能量的最低點和縱向壓強的零壓點重合,體現了熱力學自洽;在有限溫度情況強磁場下每核子自由能最低點和縱向壓強的零壓點也重合,相應的零壓點所對應的重子數密度會隨著溫度的上升而降低,隨著磁場的增加而增加.從圖2 還可以看出,在相同的重子數密度(如nB=1.5 fm?3)時,奇異夸克物質的壓強會隨著溫度的增加而增加(在零磁場下、溫度從0 提升到50 MeV時,壓強從 508.2 MeV·fm?3升高到550.3 MeV·fm?3;當B=2×1018G、溫度從0 提升到50 MeV時,橫向壓強從 607.7 MeV·fm?3升高到 650.3 MeV·fm?3).

圖2 零溫、有限溫度、強磁場下奇異夸克物質的每核子自由能/能量、壓強隨重子數密度的變化Fig.2.The energy per baryon,free energy per baryon,and the corresponding pressure as functions of baryon density with g-2 in zero temperature,finite temperature,and strong magnetic field cases.

圖3 給出了零溫、有限溫度、強磁場下奇異夸克物質的組分隨重子數密度與固定重子數密度隨磁場的變化.從左邊的兩欄可以發現,在零溫無磁場和有磁場且B=2×1018G的情況中,g-2 這套參數描述的u,d,s 三味夸克的組分會隨著重子數的增加顯著變化:在低密處,由于d 夸克的化學勢不夠大,s 夸克的粒子數密度較低,由電中性條件可知d 夸克的粒子數密度接近兩倍的u 夸克粒子數密度;隨著重子數密度增加,s 夸克化學勢增加使其粒子數密度增大,由電中性條件可令d 夸克組分降低,最終在較高密度處三味夸克的組分接近.對于溫度較高的情況(如T=100 MeV),可以發現在低密處三味夸克的粒子數密度就已經較為接近了.由于高磁場情況朗道能級的上限降低,故可以在T=0,B=2×1018G 情況中觀測到三味夸克的組分都發生了朗道能級變化而引起的“振蕩”,而此現象在高溫度情況T=100 MeV,B=2×1018G 時基本消失,這說明溫度場會減弱奇異夸克物質中強磁場的效應.為了能更好地看出強磁場與溫度場對夸克物質組分的影響,圖3 最右邊的一欄繪制了固定重子數密度nB=0.8 fm?3時三味夸克的組分在T=0與T=50 MeV 情況中隨著磁場的變化,發現零溫情況下,當磁場大于 2×1018G時,振蕩效應明顯增加;經過調試參數,考慮當溫度恰好剛剛大于50 MeV時,磁場引起的振蕩會隨著溫度的增加而基本消失,此結果更清楚地體現了溫度場對磁場效應的減弱效果.

圖3 零溫、有限溫度、強磁場下奇異夸克物質的組分隨重子數密度和磁場的變化Fig.3.The fractions of SQM as functions of baryon density and magnetic fields with g-2 in zero temperature,finite temperature,and strong magnetic field cases.

圖4 給出了不同溫度下奇異夸克物質的聲速隨重子數密度的變化,可以發現夸克物質的聲速皆小于光速,符合因果律;其次,對于T=50 MeV的情況,相同重子數密度下的聲速的平方會隨著溫度的增加而增加,這與圖2 所示的壓強隨著溫度增加而增加的結論自洽,預示著溫度升高可能會支持更大質量的致密星體.

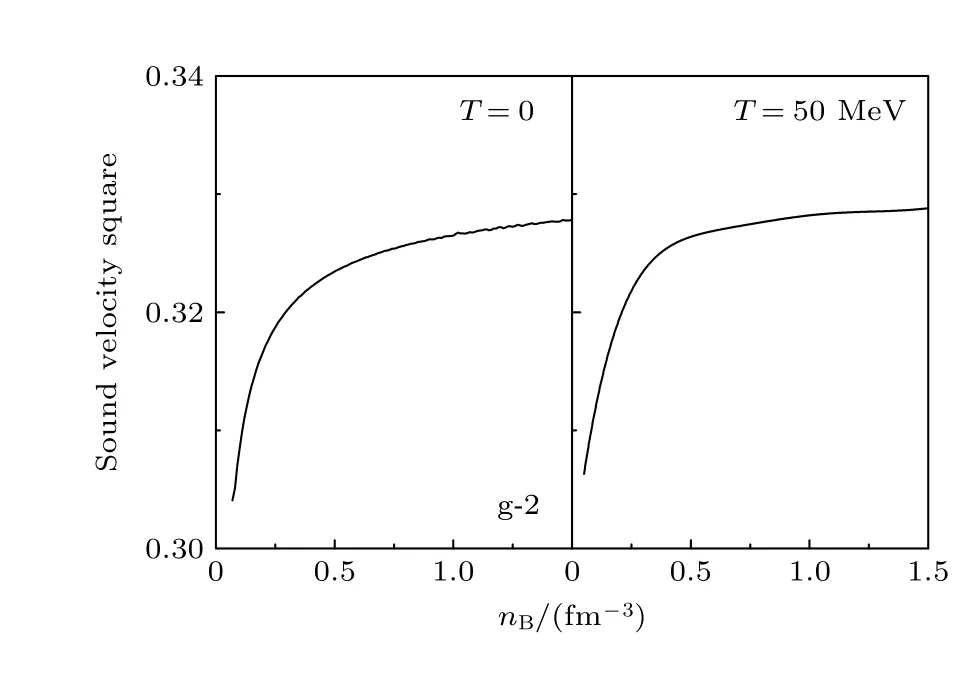
圖4 不同溫度下奇異夸克物質的聲速隨重子數密度的變化Fig.4.The sound velocity of SQM as functions of baryon density with g-2 at different temperatures.

4 夸克星計算結果

本文在星體的演化線上選取了三個等熵階段來研究強磁場、有限溫度情況下的夸克星,這類星體我們稱之為原生磁星,具體的等熵階段定義如下:

在之前的描述原生致密星體的工作[33,87–91]中,第一個等熵階段出現在超新星剛剛爆發之后,人們將每核子熵設為1,中微子和電子的比例設為0.4(Yl=Ye+Yμ+Yνe+Yνμ=0.4);在第二個階段,中微子在逃逸過程中會對原生星進行加熱,此時的每核子熵增加到2;最后一個階段,星體開始冷卻并最終形成零溫夸克星.

對于磁場下的原生星,如何定義磁星內部磁場的強度和方向分布是首要問題.對于磁星,從表面到中心的磁場強度會隨著半徑或者磁星物質重子數密度變化而變化,故人們一般通過引進密度相關磁場來描述磁星內部磁場強度的分布[49,50,53,54],可以寫作:

這里Bsurf表示磁星表面的磁場,定義其大小為1×1015G,n0是正常核物質飽和密度,B0是決定磁星內部磁場強度大小的參數值,β0和γ可以通過調節磁星內部磁場強度的重子數密度依賴性來模擬磁星內部磁場強度分布,這里采用之前工作[92]中的較快減弱的磁場強度情況參數值(fast-B profile:γ=3,β0=0.001).從文獻[92]中的圖3可以看到,我們選取了 兩種磁星內部磁場強度衰減的方案以及內部磁場隨重子數密度的變化.由于磁星內部磁場強度具體分布未知,所以定義了“快速”與“慢速”下降方式.相比于“慢速”下降的參數取值,“快速”下降模式對磁星內部重子數的依賴程度更強.為了給出比較合理且平滑的磁場隨重子數密度的下降曲線,經過調試,選擇了γ=3,β0=0.001,使得星體表面磁場較弱(慢速下降會使得表面磁場較強)且重子數依賴平滑,對整個星體質量影響較小;調節參數B0時發現,如果選取B0=4×1018G,那么對于一般磁星的最大質量中心密度處的磁場可達到較為合理的B=1×1018G,同時在夸克星的表面處壓強劈裂非常小.

由于磁星內部磁場強度與方向分布信息未知,故采用之前工作[92]的兩種磁星內部磁場方向分布:第一種假設內部磁場沿著半徑方向,我們稱之為“徑向磁場”;另一種內部磁場分布是磁場在垂直于半徑方向的平面隨機分布,我們定義為“橫向磁場”.對于第一種情況,徑向磁場會從一端傳出并從另一端返回來保證無源;磁星表面磁場由于強度太低,表面的磁場效應以及外部磁場的磁效應可以近似忽略.由此定義,可以通過這兩種非常極端的磁場方向分布情況來求解磁星的質量.

圖5 描述了零溫磁星內部磁星中心壓強以及磁星的最大質量按照兩種極端磁場方向分布情況隨B0的變化,仍選取g-2 這套參數.發現隨著B0的增加,中心壓強和磁星的最大質量都出現了一定的“劈裂”,這說明磁星內部磁場方向對磁星物質的熱力學性質以及磁星的最大質量都有影響.如果定義磁星內部壓強的不對稱度為由圖5 可知,在B0較小的時候,壓強與磁星隨著磁場方向分布的劈裂很小,隨著磁場強度的增加,橫向壓強增加、縱向壓強降低.當B0=4×1018G時,可以發現中心密度處壓強的不對稱度達到17%(對于從磁星中心到表面處的壓強不對稱度皆小于此值).圖5 中的上圖繪制了磁星最大質量對應的半徑隨磁場的變化,可以發現橫向磁場的最大質量半徑隨著磁場的增加而增大,反之,徑向磁場情況隨著磁場增加而降低.在圖5的下圖中,定義磁星最大質量不對稱度為這里M⊥和M||分別代表了橫向磁場情況與縱向磁場情況對應的磁星質量.可以發現,在磁場強度和溫度為零的 時候,g-2 這套參數能夠給出2.01 倍太陽質量夸克星,可描述PSR J0348+0432(質量為(2.01±0.04)M⊙[27]).在磁場增大的時候,橫向磁場情況M⊥增加、縱向磁場情況M//減小.當B0=4×1018G時,發現磁星質量不對稱度達到5%.由此可以得到結論:基于準粒子模型的磁星最大質量與磁星內部磁場強度和方向分布密切相關,會隨著橫向磁場的增加而增加,隨著徑向磁場的增加而減少.

圖5 零溫磁星中心壓強以及磁星最大質量與對應半徑按徑向分布與橫向分布隨 B0的變化Fig.5.Pressure f or the central density,the maximum mass of magnetar,and the radius of longitudinal orientation case and transverse orientation case as functions of B0.

圖6 給出了基于準粒子模型考慮徑向磁場P||與橫向磁場P⊥情況的原生夸克星演化中不同等熵階段的原生磁星質量半徑關系,仍沿用g-2 這套參數.在磁星強度分布里,在密度相關磁場中使用B0=4×1018G,可以看到,在圖6的左圖中,原生夸克星在T=0和B=0 情況下能夠給出2.01 倍太陽質量夸克星,可描述PSR J0348+0432(質量為2.01±0.04M⊙[27]);考慮到有限溫度的情況,當磁場為零時在等熵階段I(II)S/nB=1,Yl=0.4(S/nB=2,Yl=0)中,發現夸克星的最大質量可以提升到 2.03M⊙(2.05M⊙),這意味著在準粒子模型的框架下,零磁場原生星的最大質量隨著原生星的加熱過程而增加.在考慮磁場之后,原生星在不同等熵階段所對應的質量半徑關系會隨著徑向、橫向磁場分布的選擇而劈裂.從圖6 中圖和右圖可以看出,兩幅圖中的磁星的最大質量確實隨著徑向/橫向磁場的選擇發生了劈裂:對于S/nB=1,Yl=0.4 階段,原生磁星的最大質量降低/增加到 1.99M⊙/2.06M⊙;對于S/nB=2,Yl=0 階段,原生磁星的最大質量降低/增加到 2.02M⊙/ 2.08M⊙.這些結果表明不同等熵階段原生磁星的最大質量會隨著磁星內部磁場方向分布的徑向/橫向情況而減少/增加.計算結果表明,當選擇密度相關磁場B0=4×1018G,γ=3,β0=0.001(fast-B profile)時,磁星的中心磁場在S/nB=1,Yl=0.4 階段分別為7.8×1017G和 7.3×1017G;對于S/nB=2,Yl=0階段,磁星的中心磁場分別是9.3×1017G和8.5×1017G,說明選取的這套參數實際上磁星內部磁場強度并不算大.

圖6 原生星演化中不同階段的原生磁星質量半徑關系Fig.6.Mass-radius relations of the stages along the star evolution line of PQS with g-2 under the density-dependent magnetic field.

圖7 給出了原生磁星在不同等熵階段核心溫度隨磁星中心密度的變化,這里考慮零磁場情況和B0=4×1018G,γ=3,β0=0.001(fast-B profile)兩種情況.從圖7 可以看出,對于S/nB=1,Yl=0.4和S/nB=2,Yl=0 兩個階段,核心溫度皆隨著中心密度的增加而增加;當固定中心密度時,可以發現核心溫度會隨著磁場的增加而增加,S/nB=2,Yl=0 階段的核心溫度要高于S/nB=1,Yl=0.4的核心溫度.計算結果表明,不考慮磁場時,原生磁星在S/nB=1,Yl=0.4 階段的最大質量情況的核心溫度為12.1 MeV,在S/nB=2,Yl=0 階段為27 MeV.當考慮磁場后,磁星質量半徑關系發生劈裂,S/nB=1,Yl=0.4 階段在縱向/橫向磁場情況的的最大質量情況的核心溫度變為15 MeV/11.7 MeV;在S/nB=2,Yl=0 階段,縱向/橫向磁場情況的核心溫度變為27.5 MeV/26.9 MeV,這說明原生磁星最大質量的核心溫度不但與原生星演化中的加熱過程有關,與磁星內部磁場強度和方向的分布也有關系.

圖7 磁場與零磁場下原生星核心溫度隨中心密度的變化關系Fig.7.The core temperature for the star matter as a function of the central baryon density under zero magnetic field and B0=4×1018 G.

圖8 考慮了磁星內部磁場方向分布的綜合情況,即同時考慮縱向與橫向磁場方向分布.這里將合磁場的方向與徑向的偏移角度記為θ,在圖8 中考慮g-2 參數、密度相關磁場參數為B0=4×1018G,計算了基于不同θ角的零溫磁星質量半徑關系.磁場為零時,g-2 參數所能給出的夸克星最大質量為2.01M⊙;當同時考慮橫縱向 磁場且θ=10?或θ=15?時,磁星最大質量分別提升到2.11M⊙與2.17M⊙,反映出磁星最大質量與磁場方向和徑向方向夾角的變化規律.在磁星內部,目前還不能確定其磁場強度與方向的分布,對于更一般的磁星內部磁場方向分布方案,在今后的工作中我們會持續深入討論.

圖8 縱向、橫向磁場情況都考慮時,在g-2 參數、B0=4×1018 G 情況下基于不同 θ 角所計算的零溫磁星質量半徑關系Fig.8.Mass-radius relation for magnetars at zero temperature with g-2 and B0=4×1018 G at different θ.

5 總結

本文基于準粒子模型,研究了零溫、有限溫度、強磁場、有限溫度強磁場下的 夸克物質的對稱能、物態方程、組分等性質,發現溫度場與磁場對奇異夸克物質的的每核子能量、每核子自由能、壓強等熱力學量影響非常大.

之后著重研究了在原生星演化中不同等熵階段的原生磁星性質,采用 了密度相關磁場和兩種極端磁場方向情況給出磁星內部磁場分布.結果表明原生磁星的星體質量、半徑、核心溫度、中心密度都會很大程度上受到溫度場與磁場的影響.另外在中子星中,如果磁星內部磁場超過臨界值(如Bcr=1×1018G),超子物質就有可能變得不穩定(原因可以來自磁場對星體物質壓強的負貢獻以及星體中心磁場的取值和磁場位形的參數化關系),這種不穩定性給中子星中心磁場設定了一個自然的上限[93],在今后工作中討論核子夸克一階相變對應的混合星物質時,可以考慮此限制.

因此本文的結論是夸克星內部的溫度與磁場效應對于夸克星物質的熱力學性質非常重要,原生磁星的最大質量不僅與星體演化中的加熱過程有關,還與磁星內部磁場強度、方向分布密切相關.