尖化前緣局部稀薄氣體效應(yīng)對氣動熱影響研究

高瑩瑩，陳政偉，謝 飛，趙小程，楊凱威

（北京航天長征飛行器研究所，北京，100076）

0 引 言

隨著洲際導(dǎo)彈、返回式衛(wèi)星、載人飛船和航天飛機的研制，飛行器在稀薄氣體中飛行的時間越來越長，高度在80～100 km的空氣密度大約只有海平面的1/106～1/105，飛行器處在稀薄氣體環(huán)境之中，高空、低密度帶來的稀薄氣體效應(yīng)已經(jīng)開始顯現(xiàn)為了獲得較好的氣動性能，目前先進飛行器的前緣應(yīng)具有尖化的邊緣，局部小尺寸外形也同樣是稀薄氣體效應(yīng)產(chǎn)生的契機。

理論研究方面，王智慧等開展了多項尖化前緣稀薄氣體效應(yīng)理論研究[1～3]，黃飛等分析尖化前緣稀薄效應(yīng)對熱流的影響[4]，戎宜生等開展了過渡流區(qū)圓柱體駐點熱流的工程計算[5]，歐吉輝等進行了有局部稀薄氣體效應(yīng)的流動數(shù)值模擬[6]；試驗研究方面，陳星開展了不同球頭半徑的駐點熱流實驗測試[7]，吳松等開發(fā)了小型化的熱流傳感器[8]。但目前尚未開展前緣半徑小于2 mm的尖化前緣熱環(huán)境研究。

判斷不同氣體稀薄程度的相似參數(shù)為克努森數(shù)（下文稱Kn數(shù)），其定義為分子平均自由程λ與流動特征尺度L的比值。尖前緣飛行器在近空間大氣層飛行時，由于飛行器本身尺寸較大，所以從整體Kn數(shù)判斷，整體上還處于連續(xù)流區(qū)域，但是由于尖前緣的曲率半徑很小，且駐點附近流場梯度很大，在局部區(qū)域內(nèi)，流場的特征尺度很小，致使該區(qū)域Kn數(shù)很大，稀薄氣體效應(yīng)顯著。而這一局部區(qū)域，正是飛行器設(shè)計中氣動加熱最嚴重的駐點附近區(qū)域，因此有必要引入當?shù)豄n數(shù)或局部Kn數(shù)的概念，記為Knlocal，其定義為

式中Q可以為溫度、密度等；l為流場中兩點間的距離；Knlocal由于考慮了流場中某一點的當?shù)胤肿悠骄杂沙毯彤數(shù)亓鲌鎏荻却笮。虼烁芫_地刻畫流場的當?shù)叵”〕潭取?/p>

隨著Kn數(shù)的增加，稀薄氣體效應(yīng)越來越顯著。對于大尺寸外形，稀薄氣體效應(yīng)增加的主要因素在于飛行高度的增加帶來的分子平均自由程λ的增大，對于尖銳外形等局部小尺寸外形，由于特征尺度減小，在較低的飛行高度下也會出現(xiàn)局部稀薄氣體效應(yīng)。

本文對飛行器尖化前緣外形進行測熱試驗，獲得前緣半徑分別為0.5 mm、2 mm和5 mm 3種小尺寸前緣半徑尖化前緣中心線熱流分布規(guī)律，分析在半徑較小的情況下的局部稀薄氣體效應(yīng)。并通過高空稀薄過渡區(qū)的熱環(huán)境預(yù)測方法與試驗結(jié)果進行比較，評估稀薄氣體效應(yīng)對氣動熱環(huán)境的影響。

1 尖化前緣風(fēng)洞測熱測壓試驗

1.1 試驗?zāi)Ｐ?/h3>

由于飛行器外形頭部附近的熱流最高，因此試驗截取頭部附近長為650 mm的區(qū)域作為尖化前緣理論外形。為比較不同尖化前緣半徑的熱流分布規(guī)律，研究局部稀薄氣體效應(yīng)，在理論外形的基礎(chǔ)上修改前緣半徑，加工3組前緣半徑R分別為5 mm、2 mm、0.5 mm的尖化前緣外形作為試驗?zāi)Ｐ汀ＤＰ桶惭b在風(fēng)洞中如圖1所示。

圖1 試驗?zāi)Ｐ?Fig.1 Model at the Wind Tunnel

1.2 試驗狀態(tài)

本次試驗在中國科學(xué)院力學(xué)研究所高溫氣體動力學(xué)國家重點實驗室JF8A和JF10風(fēng)洞中進行，試驗的流場狀態(tài)參數(shù)見表1，試驗攻角均為0°。

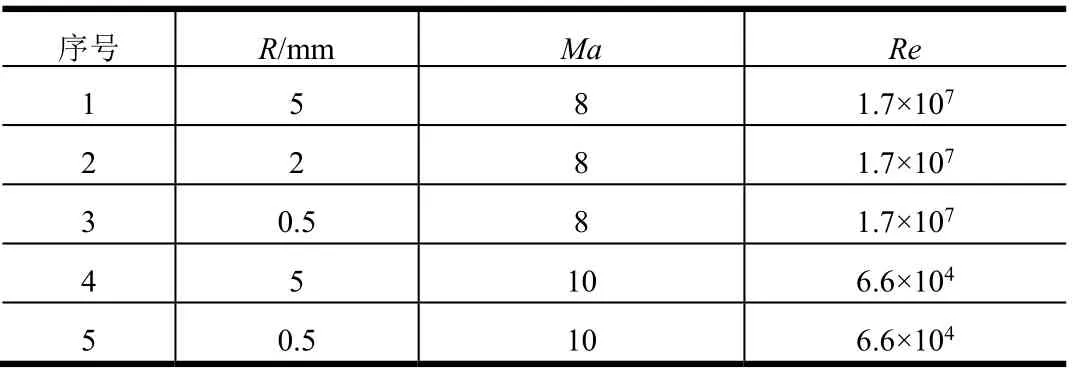
表1 試驗狀態(tài)參數(shù) Tab.1 Experiment Condition

1.3 試驗結(jié)果

分別對表1的5種試驗狀態(tài)進行了測熱測壓試驗。試驗測得的駐點熱流如表2所示。

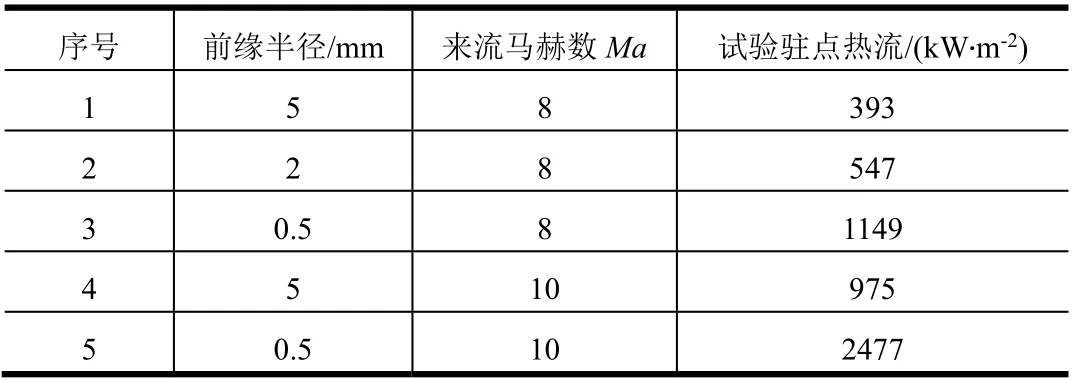
表2 駐點熱流試驗結(jié)果 Tab.2 Experiment Stagnation Heat

5種狀態(tài)的尖化前緣中心線無量綱熱流（均以駐點無量綱化）分布比較如圖2所示，可以看出分布基本一致，均在駐點至50 mm處下降到50%以下。

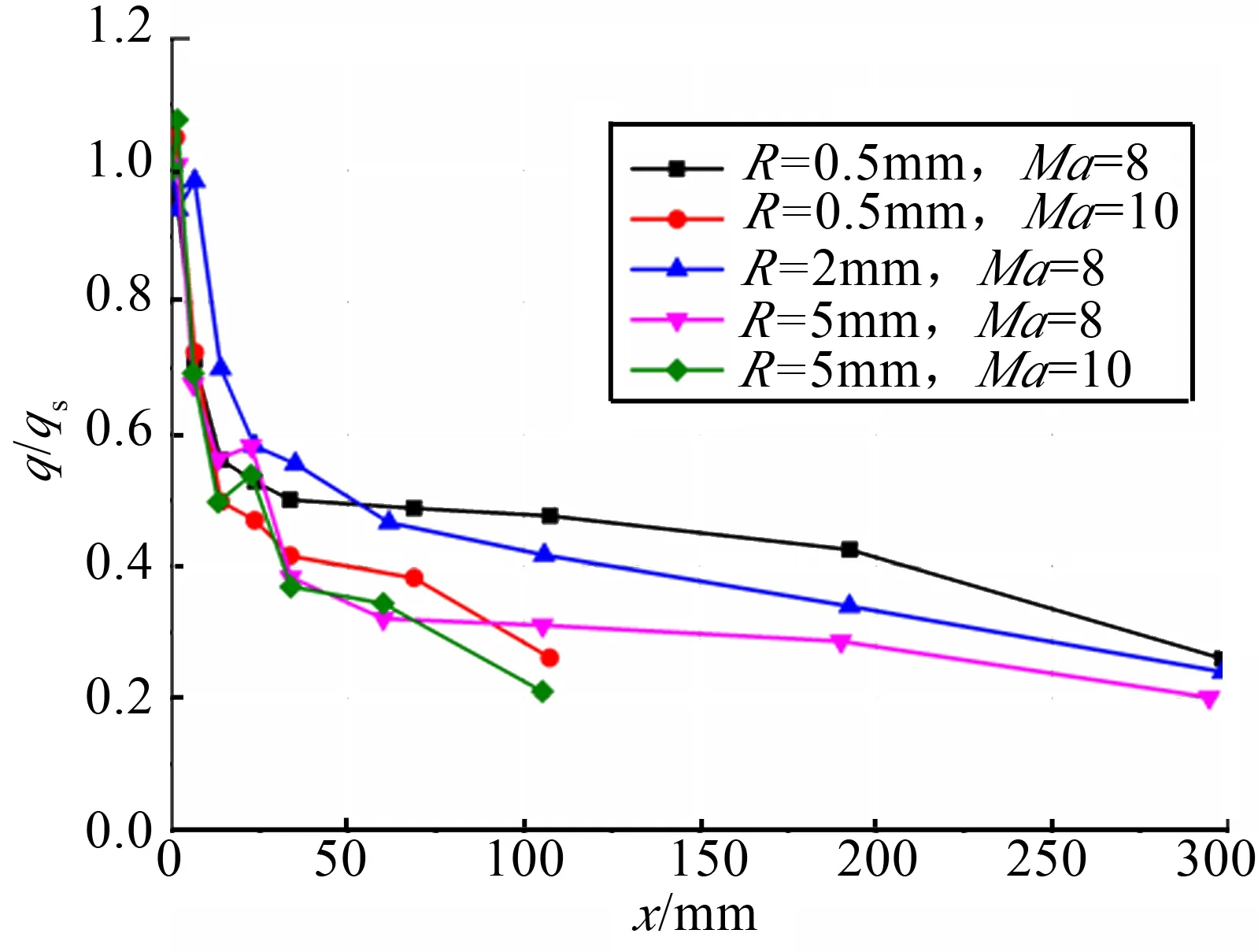
圖2 前緣中心線無量綱熱流分布 Fig.2 Leading Edge Nondimensional Heat

2 尖化前緣稀薄氣體效應(yīng)研究

2.1 駐點熱流公式適用性研究

三維球頭駐點熱流常用的Fay-Riddell公式為

式中qs為駐點熱流；Pr為普朗特數(shù)；ρsw為壁面氣體密度；μsw為壁面氣體粘度；ρs為駐點氣體密度；μs為駐點氣體粘度；ve為邊界層外緣速度；s為沿母線長度；Le為劉易斯數(shù)；hd，hs，hw分別為離解焓、駐點焓、壁面焓。

為了驗證Fay-Riddell駐點熱流計算公式在半徑非常小的情況是否能夠適用，需要通過Fay-Riddell公式和試驗測量結(jié)果進行比較。計算結(jié)果與試驗結(jié)果比較如表3所示。當半徑R=0.5～5 mm、Ma=8時，駐點熱流與Fay-Riddell公式值偏差小于10%；當半徑R=5 mm、Ma=10時駐點熱流與Fay-Riddell公式值偏差依然小于10%；但當半徑R=0.5 mm、Ma=10時駐點熱流低于Fay-Riddell公式值29.5%，說明此狀態(tài)下外形存在局部稀薄氣體效應(yīng)。隨著外形尺寸減小和稀薄程度的增加，F(xiàn)ay-Riddell公式計算結(jié)果與試驗值差別增大，在小尺寸下已不再適用，需要考慮局部稀薄氣體效應(yīng)對氣動熱的影響。

表3 駐點熱流結(jié)果比較 Tab.3 Comparison of Stagnation Heat

2.2 局部稀薄氣體效應(yīng)計算

錢學(xué)森根據(jù)Kn數(shù)范圍，將流動劃分為連續(xù)流、滑移流、過渡流、自由分子流，其中連續(xù)流和滑移流為連續(xù)流區(qū)，過渡流和自由分子流為稀薄流區(qū)，劃分標準如下[9]：

a）連續(xù)流領(lǐng)域（Kn＜0.01），符合連續(xù)介質(zhì)假設(shè)，可以用N-S方程描述；

b）滑移流領(lǐng)域（0.01≤Kn＜0.1），物面滑移邊界條件，需要求解滑移邊界條件下的N-S方程，工程上可將滑移流合并到連續(xù)流；

c）過渡流領(lǐng)域（0.1≤Kn＜10），滑移流區(qū)的上限和自由分子流的下限之間的區(qū)域，從理論上難以處理，常用DSMC方法計算[10,11]，工程上常利用連續(xù)流和自由分子流結(jié)果，采用橋函數(shù)加權(quán)平均；

d）自由分子流區(qū)（Kn≥10），采用無碰撞項的Boltzmann方程[12,13]，工程上使用簡化的熱流計算方法。

自由分子流區(qū)熱流密度計算工程計算方法如下：

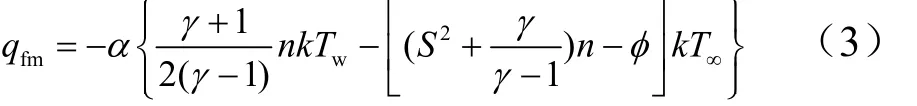
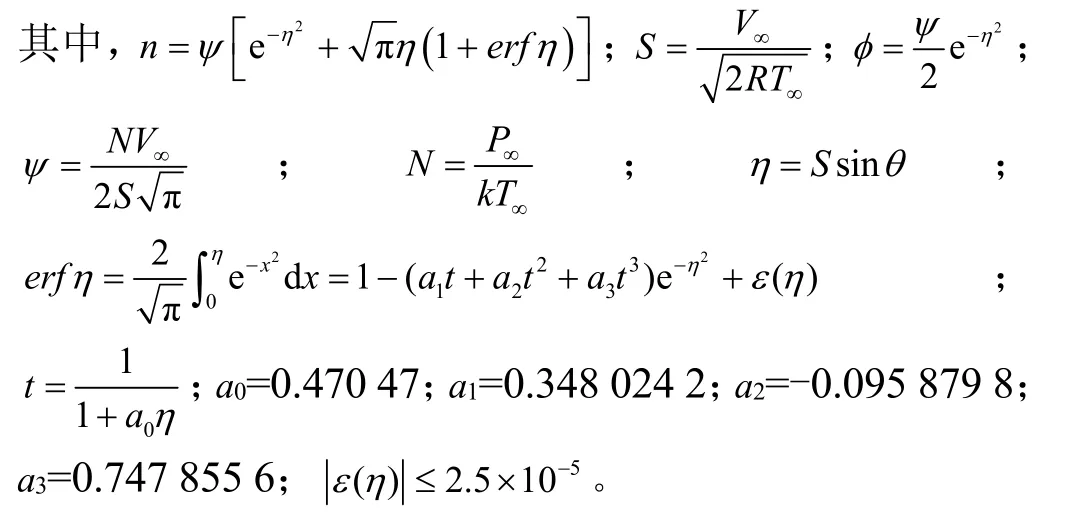
式中α為適應(yīng)系數(shù)；θ為氣流與物面夾角；k為玻爾茲曼常數(shù)；R為理想氣體常數(shù)；P∞為自由流壓力；T∞為自由流溫度；V∞為自由流速度；Tw為壁溫。

過渡區(qū)熱環(huán)境計算首先計算連續(xù)流假設(shè)下的熱流qc，再計算自由分子流假設(shè)下的熱流qfm，最后采用橋函數(shù)方法進行搭接。通常采用Matting橋函數(shù)[14]、Nomura橋函數(shù)[15]、線性橋函數(shù)方法計算過渡區(qū)熱環(huán)境。其中Matting橋函數(shù)方法如下式：

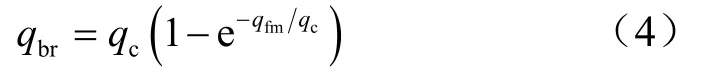
采用Matting橋函數(shù)計算前緣半徑分別為5 mm、 2 mm、0.5 mm的尖化前緣外形Kn數(shù)以及過渡區(qū)熱流與熱流測量值及Fay-Riddell公式比較如表4所示。

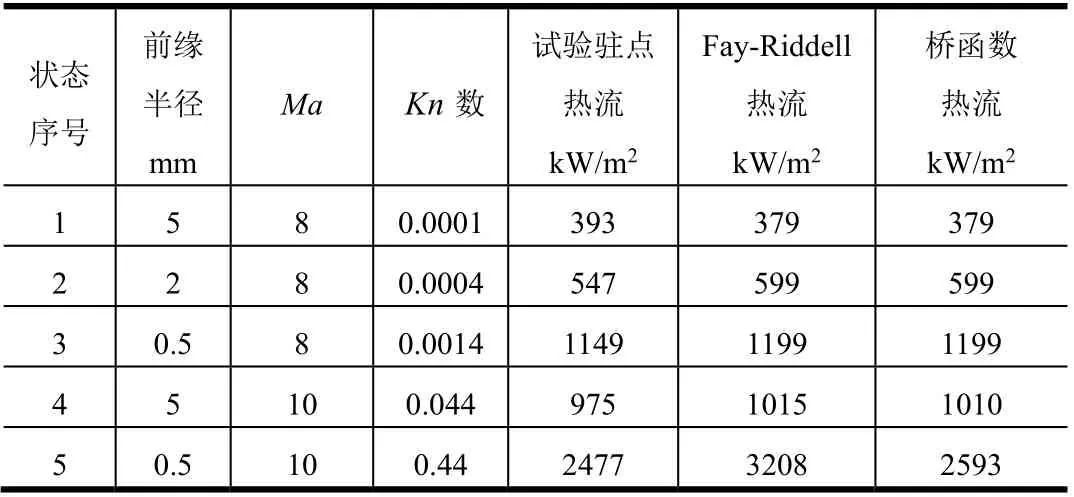
表4 熱流測量值與Fay-Riddell公式及橋函數(shù)結(jié)果的比較 Tab.4 Comparison of Stagnation Heat between Experiment、 Fay-riddell Formula and Bridge Function

由表4可以看出，隨著前緣半徑的減小，Kn數(shù)越大，流動稀薄程度越高。Ma=8條件下不同前緣半徑對應(yīng)的Kn數(shù)均小于0.01，流動仍屬于連續(xù)流，局部稀薄氣體效應(yīng)并不明顯。Ma=10、R=5 mm時，Kn數(shù)在0.01～0.1之間，流動狀態(tài)屬于滑移流；Ma=10、R=0.5 mm時，Kn數(shù)在0.1～10之間，流動狀態(tài)屬于過渡流。因此R=0.5 mm出現(xiàn)局部稀薄氣體效應(yīng)，采用橋函數(shù)搭接方法計算的熱環(huán)境與實際測量結(jié)果符合的較好。考慮稀薄氣體效應(yīng)后的實際熱流比連續(xù)流計算的偏小，這對熱防護是有利的。

3 結(jié) 論

通過研究得到如下結(jié)論：

a）對于較小尺寸的尖化前緣飛行器，在80 km以下的高度已經(jīng)出現(xiàn)了局部稀薄氣體效應(yīng)，并且局部稀薄氣體效應(yīng)隨著尖化前緣球頭半徑的降低和高度的增大變得更加顯著；

b）橋函數(shù)計算過渡區(qū)熱環(huán)境結(jié)果與試驗結(jié)果符合較好，考慮稀薄氣體效應(yīng)后的實際熱流比連續(xù)流計算的偏小。

綜上所述，對于氣動熱環(huán)境的工程評估，當出現(xiàn)高度增大或局部尺寸減小時，有必要考慮稀薄氣體效應(yīng)，需要采用橋函數(shù)進行稀薄過渡區(qū)的熱環(huán)境預(yù)測，以便更加準確地評估稀薄氣體效應(yīng)對氣動熱環(huán)境的影響。