基于遠場疊加公式的箔條陣列雷達散射特性研究

劉 鑫，王雪松，孟 剛，劉佳琪，李猛猛

（1. 國防科技大學，長沙，410073；2. 試驗物理與計算數學重點實驗室，北京，100076；3. 南京理工大學，南京，210094）

0 引 言

國內外學者針對箔條形式不斷進行優化，提出了各種新型的箔條結構。楊坤龍提出的三維正交（坐標軸型）箔條較相同質量的傳統箔條，平均雷達散射截面積（Radar Cross Section，RCS）提高了2.61 dB[7]；劉鑫提出了一種基于角反射器的箔條RCS 增強結構，使其相比單個箔條的RCS增大了30 dB以上[8]；甘琳提出了一種由傳統箔條串接而成的間斷型長箔條[9]等。

隨著箔條樣式的不斷豐富，尺度的不斷增加，對復雜構型大尺度箔條陣列的電磁特性仿真分析帶來了新的挑戰。本文針對常規仿真方法計算量大，計算耗時長等問題，提出利用遠場疊加公式與多層快速多極子算法（Multilayer Fast Multipole Algorithm，MLFMA）相結合的快速仿真分析方法，利用快速多極子法，完成箔條單體的精確建模和計算，并通過遠場疊加法，快速得到箔條大陣列的遠場分布。文中選取坐標軸型和米字型兩種異型箔條作為分析案例，研究了兩種異型箔條的散射特性，完成了算法適應性分析和精度分析。提出的米字型箔條是在坐標軸型箔條的基礎上發展的改進型箔條，分析結果顯示，通過結構優化，可進一步增強箔條回波，改善干擾效果，為箔條的優化設計提供了支撐。

1 仿真模型介紹

1.1 箔條散射單元與箔條陣列

為分析分布尺度為公里級的箔條雷達散射特性，本文首先采用MLMFA對單個箔條散射單元進行精確建模仿真，并通過遠場疊加公式，求得大尺度箔條陣列的雷達散射截面（Radar Cross section，RCS）。

箔條散射單元結構示意如圖1所示，首先對兩種不同形式的箔條散射單元進行建模分析，圖1a為坐標軸型箔條散射單元結構，由3根長度為75mm，直徑為2 mm的偶極子兩兩相互垂直組成；圖1b為米字型箔條散射單元結構，是在坐標軸型箔條散射單元水平面上的十字型偶極子增加兩根偶極子，形成米字型散射單元。分別用以上2種不同形式的箔條組成箔條陣列，箔條陣列排布如圖2所示，散射單元中心間隔75mm，沿x軸均勻排布。

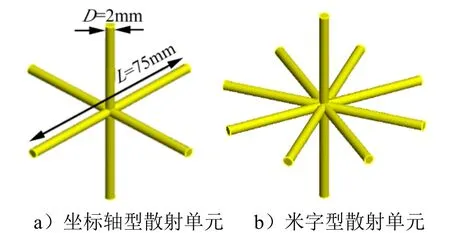
圖1 兩種箔條散射單元結構示意 Fig.1 The Structure of Three Kinds of Chaff Scattering Units

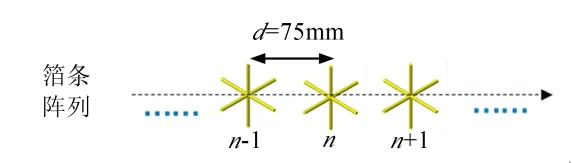
圖2 箔條陣列示意 Fig.2 Schematic Diagram of Chaff Array

1.2 遠場疊加公式

設有一個N×N單元的矩形柵格矩形平面陣列，放置在xy平面內，行間距為dx，列間距為dy，如圖3所示。

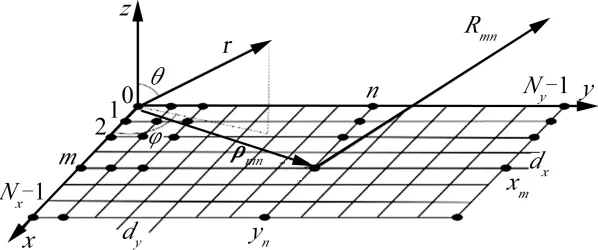
圖3 遠場疊加方法示意圖 Fig.3 Schematic Diagram of The Far-field Superposition Method

第mn個單元的坐標位置為

(2)硅化：是金礦化的主要蝕變類型。大致可分為三期，早期以深灰色細糖粒狀、微晶集合體狀及脈狀出現；成礦期呈白色不規則狀、細脈狀出現在蝕變巖的裂隙中，伴有多金屬硫化物出現，是金礦化的主要階段；晚期硅化呈灰白色、乳白色在蝕變帶內出現，形成一些石英細脈。

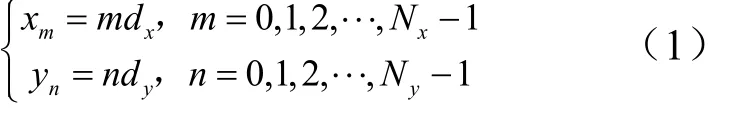
位置矢量為

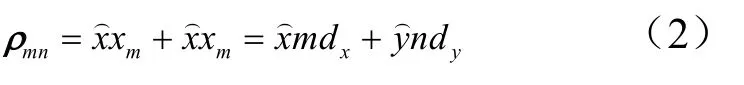
坐標原點到遠區某點的單位矢量：

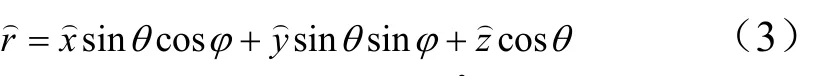
設第mn個單元的激勵電流為，則其遠區輻射場可表示為

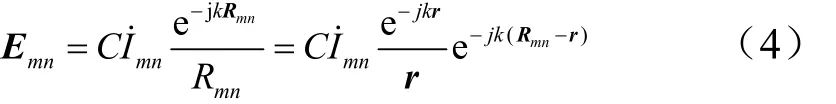
式中C為與mn無關的單元因子，并且令波程差為

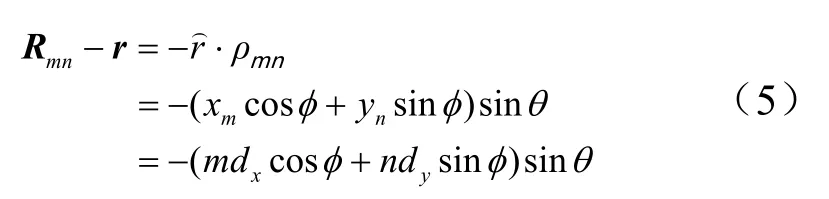
則第mn個單元的遠區輻射場為

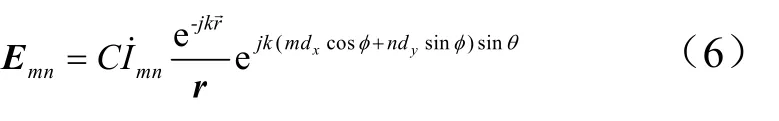
整個平面陣列的遠區輻射場為

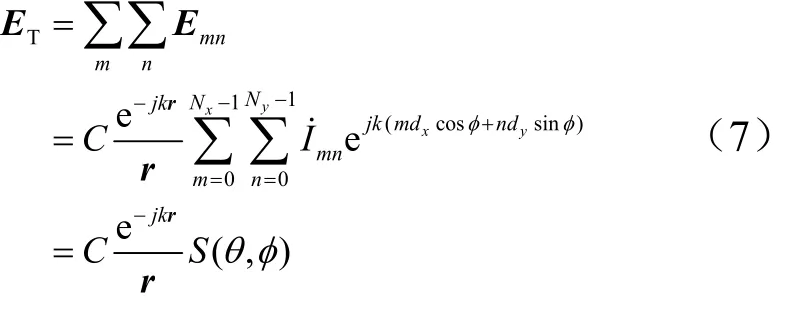
式中陣因子為

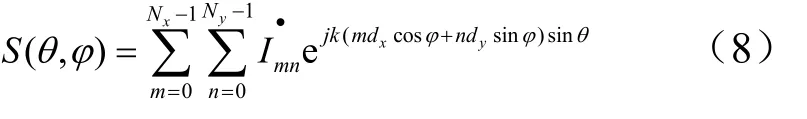
此為陣因子的常規形式，基于陣因子即可實現遠場疊加方法。

遠場疊加方法的實質為計算單個散射單元位于坐標原點處的散射場，通過不同散射單元之間的距離差計算波程差，從而計算不同位置處的散射單元的散射場，再把不同單元的散射場進行疊加求和，得到單元陣列的總散射場。

1.3 仿真數據內插

設(xi,y i),i= 0,1,…,m+n是與y=f(x)有關的m+n+1個值點，其中xi,(i= 0,1,…,m+n)互異，y i=f(xi)。有理函數插值問題即尋求有理分式函數：

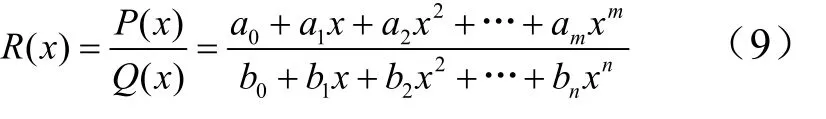
使之滿足如下條件：

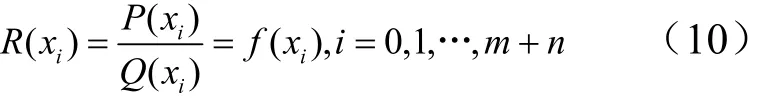
求解有很多種構造方法，本節所使用的是倒差商表構造連分式的方法，有理函數的表達式為

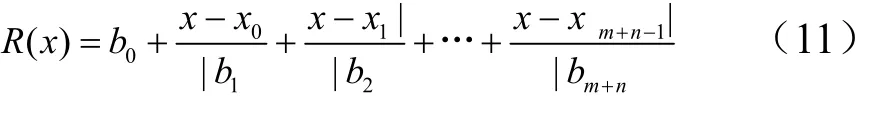
1.4 誤差計算公式

每一頻率下的RCS單位取dBm2，絕對誤差和相對誤差計算公式為

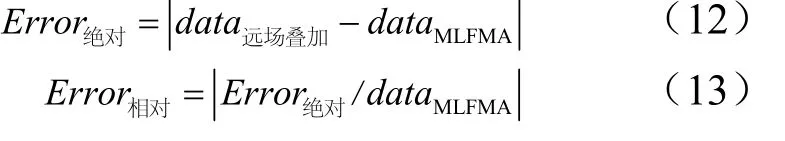
2 算例結果與分析

2.1 坐標軸型箔條散射單元

坐標軸型散射單元仿真場景如圖4所示，使用同一入射波垂直照射箔條陣列，計算不同俯仰角的雷達回波，雷達基本參數如表1所示。

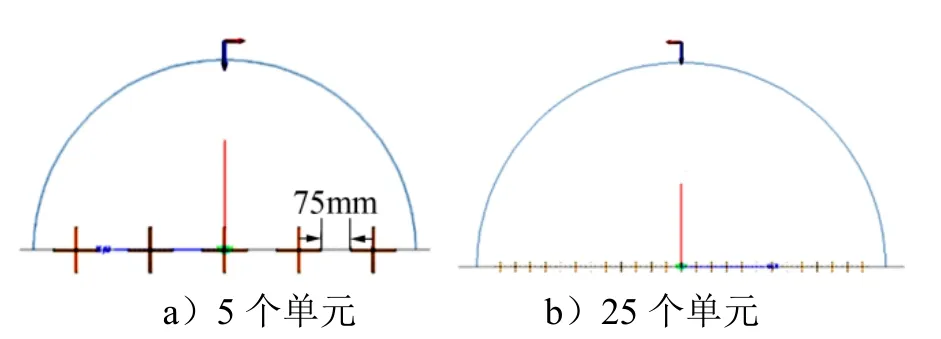
圖4 坐標軸型散射單元仿真場景 Fig.4 Simulation Scene of Three-coordinate Scattering Units

表1 雷達基本參數 Tab.1 Radar Basic Parameters

采用快速多極子法，計算出單個箔條單元的散射特性，再通過遠場疊加公式，分別得到5個、25個箔條散射單元陣列的遠場分布，與直接采用MLMFA計算的結果進行對比。不同頻率下，兩種方法計算得的散射單元陣列RCS，如圖5所示。

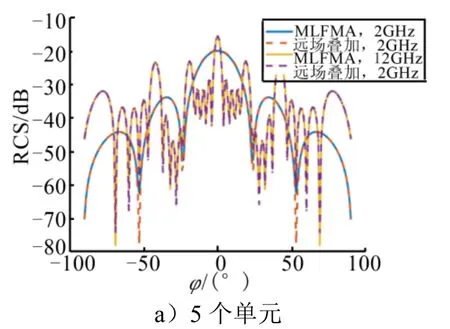
圖5 坐標軸型散射單元RCS對比 Fig.5 RCS Comparison of Three-Coordinate Scattering Units

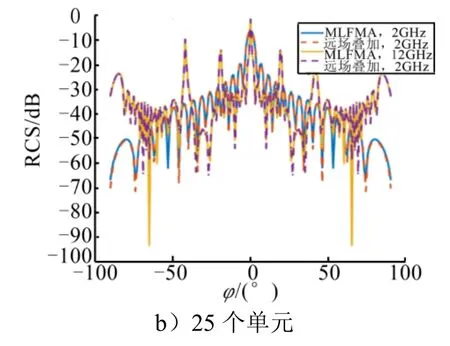
續圖5

由于該散射單元為極化對稱結構，故只分析了VV極化下的情況，且僅計算陣列排布方向與雷達入射方向所在平面的遠場分布，同時為了保持一致性，后面的計算結果也采用相同的雷達參數。由圖5可以看出，通過遠場疊加公式獲得的箔條陣列遠場RCS和MLFMA仿真數據的誤差絕大多數都在5%以內。因此，該方法精度較好，可用于快速計算大尺度箔條陣列。

2.2 散射特性對比

將坐標軸型箔條散射單元的結構改進，增加兩根偶極子形成米字型散射單元，研究其RCS增強特性。對比米字型散射單元與坐標軸型散射單元在不同頻率下，相同排布時的RCS變化，如圖6所示。

圖6 1000m坐標軸型散射單元和米字型散射單元陣列RCS對比 Fig.6 RCS Comparison of 1000m Array of Three-coordinate and Star-shaped Scattering Units

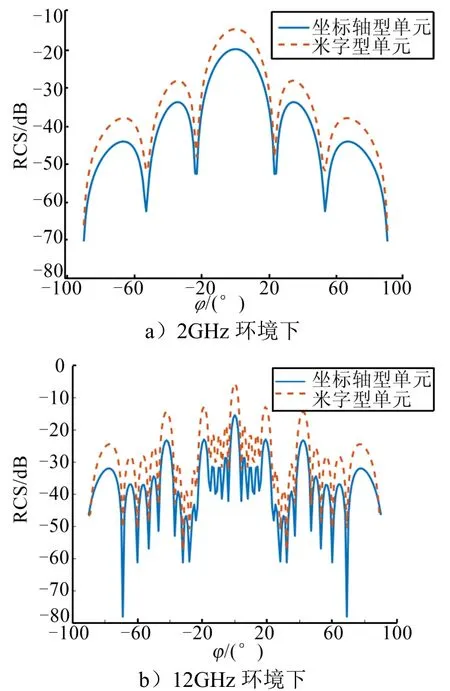
圖6 25個坐標軸型散射單元和米字型散射單元RCS對比 Fig.6 RCS Comparison of Twenty-five Three-coordinate and Star-shaped Scattering Units

分別對比了5個單元和25個單元的坐標軸型型和米字型箔條的仿真結果，米字型箔條從結構上僅比坐標軸型箔條增加了兩根箔條絲，但從仿真結果可以看出，米字型箔條相對于坐標軸型箔條，在相同排布下RCS明顯增強，增加了約8～10 dB。說明對箔條結構進行優化，是提升箔條回波強度的有效手段。

2.3 公里級箔條陣列

利用遠場疊加公式，基于25個散射單元陣列的遠場分布，計算了1000m長的箔條陣列的RCS，計算結果見圖7。從圖7可以看出，米字型箔條相對于坐標軸型箔條，在相同排布下RCS明顯增強，在主反射方向RCS增強效果最大，最高增強13 dB。

3 結 論

本文針對大尺度箔條陣列的仿真問題，提出了基于遠場疊加公式，由數個散射單元構成的小陣列快速求得公里級陣列的遠場分布；對比遠場疊加公式與MLFMA仿真獲得的陣列遠場分布結果，整體誤差較小，誤差基本在5%以內；該方法為分析大尺度的箔條陣列提供了一種新的途徑。

對比分析了坐標軸型箔條和米字型箔條的散射特性，在相同排布下，米字型RCS明顯增強，在主反射方向RCS最高增強13 dB。證明優化箔條結構，可以進一步提高箔條的干擾效率。本文的研究成果能夠為箔條干擾的優化設計提供支撐。