獨柱墩橋梁抗傾覆設計與加固方法研究
任永斌
(中交第二公路勘察設計研究院有限公司,湖北 武漢 430000)
0 引言
獨柱墩橋梁往往具備多種路線形態,能夠極大地優化局部公路交通通行環境,被廣泛應用在公路匝道橋梁、城市立交中。車輛通行規模的增大促使人們對橋梁結構承載強度及穩定性要求愈發嚴格,考慮到曲線獨柱墩橋梁只有單個支點支撐其橫橋向穩定性,在外部行車荷載作用下極容易造成獨柱墩橫向傾覆。獨柱墩曲線橋梁在偏心荷載作用下產生較大的扭矩,此時橋梁支座容易產生脫空情況,繼而產生整體傾覆,對公路交通的穩定運行造成了極大威脅。為此,開展獨柱墩曲線橋梁行車荷載下的力學加固分析具有重要社會經濟效益。
1 獨柱墩曲線箱梁受力
直線橋梁在行車荷載不偏心情況下不會產生較大扭矩,然而在曲線獨柱墩箱梁結構中,即便存在對稱行車荷載,也會對上部結構產生明顯扭矩。在橋梁曲率半徑較小時,獨柱墩曲線箱梁極容易出現內梁卸載、外梁超載情況,針對獨柱墩箱梁設計優化不僅需要考慮行車偏載情況下造成的結構內力不均勻現象,而且還要重點分析支點反力分布,避免出現傾覆危害。
1.1 荷載
相對于直線型橋梁,獨柱墩曲線箱型橋梁在行車荷載作用下,會產生扭轉、橫縱向彎曲、畸變等多種變形狀況,且隨著箱橋梁曲率半徑的變化,力學響應差異性極大。獨柱墩曲線箱橋梁在外荷載作用下產生明顯的彎扭耦合效應,產生的變形也要大于同樣尺度的直線橋梁,且曲線橋梁彎扭耦合下的外邊緣變形明顯大于內邊緣變形[1]。
1.2 支座反力
獨柱墩曲線箱橋梁支座反力在外界荷載作用下呈不均勻分布,曲線橋的外支座反力明顯要大于內支座反力,這主要歸因于橋梁重心線處于截面形心線外側。曲線橋梁支座反力比直線橋更為復雜,在內側支座處極容易出現負支座反力,繼而導致支座脫空而傾覆。為此,前期曲線橋梁設計階段需要加強支座控制,可以在外側支座位置設置防超載裝置,也可以在內側采用受拉型支座。
1.3 剛度
獨柱墩曲線箱橋梁上部結構具備較大的橫梁剛度,這能夠充分保證整體結構的剛度穩定性。施工中采用薄腹箱梁截面時,則需要適當增加橫梁數量提升剛度,以便弱化彎扭耦合造成的截面畸變。除此之外,曲線箱梁預應力效應也會對支座反力進行重分配,進行結構抗傾覆設計中支座反力分析時需要對預應力效應加以考慮[2]。
2 工程概況
湖北省某鋼筋混凝土曲線箱梁設計全長90 m,三跨結構(25 m+25 m+25 m),上跨運輸鐵路,設計荷載為公路Ⅱ級,設計車速60 km/h。橋型布置示意圖如圖1所示。曲線箱橋梁面設計寬度11 m[0.5 m(防撞護欄)+10 m(行車道)+0.5 m(防撞護欄)],橋面設計橫坡1.5%,曲率半徑700 m。箱梁結構頂板高度1.8 m,底板寬度為1 m,寬度為11 m;下部結構設計則采取獨柱墩橋墩+擴大基礎構造,U型橋臺。其中,箱梁現澆混凝土C30,橋墩、支座墊石、橋臺結構混凝土C30,搭板、護欄、橋墩擴大基礎則采取C25混凝土。支座布置方案如下:橋橋梁臺處布設3個對稱分布的板式橡膠支座(400×450×80 mm),內外側支座距離橋梁設計中線為3.2 m,中間1、2號橋墩處則分別布置單個圓板式橡膠支座(1 310×140 mm)。考慮到該區域車輛通行量較多,且重車占比較大,設計單位擬對該獨柱墩曲線箱橋梁進行公路Ⅰ級荷載的抗傾覆驗算,繼而進行結構優化加固,以便改善橋梁結構耐久性,提升區域交通規模[3]。
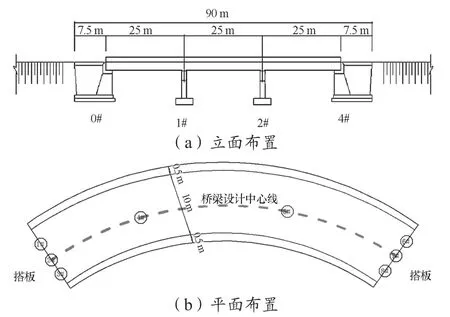
圖1 橋型布置示意圖
3 有限元模型分析
3.1 尺寸及荷載
該獨柱墩曲線箱梁為非預應力混凝土箱梁設計,設計單位主要采取MIDAS/Civil有限元軟件對該橋梁進行梁格法模型構建和力學響應分析,箱梁為單箱雙室截面設計,具體尺寸如圖2所示。
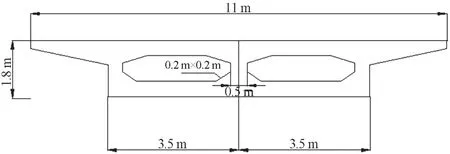
圖2 箱梁截面示意圖
模型施加荷載如下:永久荷載包括混凝土自重25 kN/m3、兩側護欄線荷載14.3 kN/m、橋面鋼筋混凝土鋪裝及瀝青混凝土路面;汽車荷載則以公路Ⅰ級設計標準進行抗傾覆驗算,橋面為雙向二車道設計,其中,公路Ⅰ級車道荷載均布荷載標準值qk=10.5 kN/m,集中荷載標準值pk按照以下標準進行選取:計算跨徑≤5 m,則選取pk=180 kN;計算跨徑≥50 m時,則選取pk=360 kN;計算跨徑分布在5~50 m之間時,則通過線性插入法選取pk。該橋梁為雙向行車,行車寬度10 m,則需要綜合分析二車道荷載效應,此時均布荷載qk=21 kN/m,集中荷載pk選取為520 kN;支座沉降以0.025 m(L/3 000)進行計算。
3.2 模型構建
項目主要采取MIDAS/Civil軟件進行梁格法模型構建,模型示意圖如圖3所示。模型計算中對于最不利荷載施加位置的確定遵循以下原則:行車均布荷載滿布于橋梁結構最不利情況影響線上,集中荷載則作用于影響線最大峰值位置。通過軟件測試可以獲取1#、3#、6#、8#支座最不利行車荷載施加位置,1#支座反力計算需要在3#支座內側加載,此時均布荷載滿布橋跨,5#支座外邊緣施加集中荷載;3#支座反力計算則需要在內側進行加載,此時橋跨滿布均布荷載,4#支座外邊緣施加集中荷載;8#支座反力計算則需要均布荷載滿布橋跨,5#支座外邊緣施加集中荷載[4]。

圖3 模型構建示意圖
3.3 抗傾覆分析
3.3.1 最不利支座反力
項目進行獨柱式曲線箱橋梁抗傾覆驗算中,需要考慮以下荷載組合:支座沉降、箱橋梁自重、護欄及橋面鋪裝、外側施加行車荷載。項目為對稱結構,依據實踐經驗,只對1#、3#支座不利情況進行分析。1#支座最不利內側加載反力、3#支座最不利外側加載造成的反力統計如表1所示。表1結果表明,1#支座最不利內側施加行車荷載下,支座反力不存在負值,所有支座并不會脫空;3#支座最不利外側施加行車荷載情況下,3#支座的反力為負值,此時3#支座存在脫空。該橋梁結構左右兩側對稱,1#支座和6#支座具備同樣力學響應,3#支座和8#支座也具備同樣力學響應。3#支座在不利荷載施加情況下出現反力負值主要是由曲線梁自身構造特性所決定,箱梁內側弧長要小于外側弧長,曲線箱梁的截面形心和結構重心并不一致,結構重心要往曲線梁外側發展,此時重心軸、行車荷載兩者產生相互扭轉,造成3#支座的脫空現象,引發橋梁翻轉等嚴重安全事故[5]。

表1 1#、3#支座不利情況下支座反力統計
3.3.2 抗傾覆驗算
依據相關規范,該文確定該曲線箱梁的最小抗傾覆系數為2.5,這樣才能夠確保箱梁結構的強度耐久性符合要求。該獨柱墩曲線箱梁抗傾覆安全系數計算如式(1):

式中,RGi——各支座反力;e——行車加載車道到結構傾覆中線距離最大值;Ω——橫線加載車道和傾覆中線圍合面積;u——沖擊系數;xi——支座至傾覆線之間的距離,如表2所示。

表2 傾覆線至支座的垂直距離統計
項目箱梁均布荷載21 kN/m,集中荷載520 kN,Ω=191 m2,沖擊系數u為0.24,加載車道至傾覆線距離e為2.8 m,則通過計算可獲取項目的抗傾覆系數為1.3<2.5,則該曲線箱型橋梁在Ⅰ級公路荷載下不能夠達到穩定性要求。
4 橋梁加固優化設計
4.1 加固方案
新建曲線橋梁可以通過支座的合理偏心化設置有效提升結構的抗傾覆能力。既有箱梁結構則難以進行支座偏心處理,設計單位擬采取增加支座數量方法進行抗傾覆優化。加固方案中需要在箱梁已有獨柱墩上部施工鋼結構支撐,支撐上需要附聯2個支座,對行車荷載及彎扭耦合效應進行充分分擔,消除過大的橫向扭矩。加固布置示意圖如圖4所示,1、2號橋墩位置在橋梁設計中心線兩側距3.2 m處分別布置1個同類型支座,該布置形式能夠弱化行車荷載偏心施加時產生的彎扭變形[6]。
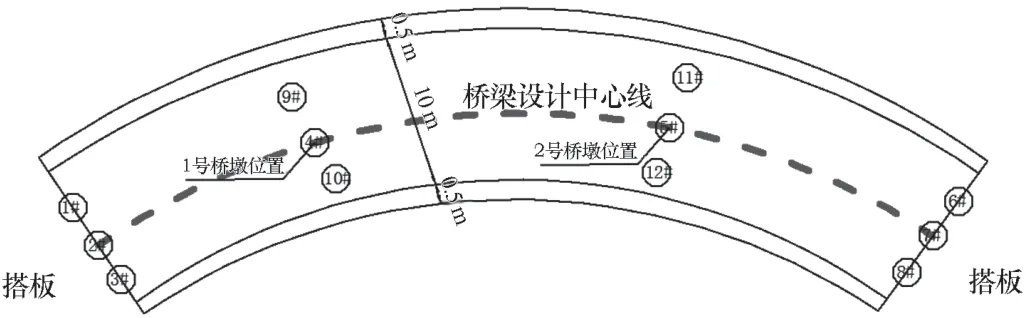
圖4 加固方案支座布置示意圖
4.2 加固效果
針對加固后工況開展原有最不利荷載作用下的有限元分析,3#支座加固前后各支座反力及抗傾覆安全系數對比如表3所示,結果表明,公路Ⅰ級行車荷載作用下,加固后曲線橋梁都不會出現支座脫空情況,3#支座反力此時為420 kN。

表3 不利情況支座反力及抗傾覆安全系數對比
5 總結
該文針對湖北省某三跨獨柱墩曲線箱梁進行抗傾覆驗算,并且針對最不利支座進行加固分析。研究結果表明,公路Ⅰ級荷載作用下原有橋梁存在3#支座脫空情況,極容易出現傾覆危害;采取增加中墩支座的加固方案能夠充分提升橋梁通行能力及整體結構的穩定性。該文所作研究能夠為類似工程設計提供理論參考。

