離散事件動態系統的輸出調節

楊弘博，呂 鵬，殷 翔*，李少遠

(1.上海交通大學電子信息與電氣工程學院，上海201100；2.上海交通大學自動化研究所，上海200030)

離散事件動態系統(discrete-event dynamic system,DEDS)被廣泛應用在邏輯任務和離散對象的建模上[1-3].為了約束DEDS，使其適應復雜任務的要求，Ramadge等[4]提出了監控理論(supervisory control theory,SCT).SCT是一種可證明的DEDS控制器綜合形式化方法，本質上通過邏輯反饋使得受控DEDS的邏輯正確.此后SCT得到了廣泛發展，如Lin等[5]和Rudie等[6]研究了DEDS的可觀測性，Ushio等[7]和Yin等[8]研究了具有非確定輸出函數的米利自動機監控問題.隨著研究的不斷深入，SCT在工業[9]、交通運輸[10]和醫療行業[11]等眾多領域得到了廣泛的應用.

對DEDS的表征進行控制有著重要的現實意義.其中“表征”定義在系統事件上，是事件的函數.它既可以是真實的輸出，也可以是虛擬的屬性，稱之為系統的“輸出”.比如在故障檢測問題中，輸出可以建模表達相關儀表的讀數.然而DEDS的事件主要用于刻畫系統的內部行為，且現有SCT主要也研究系統內部行為本身是否符合某些事件序列組成的規約，無法按照由事件的函數組成的規約實現控制.所以，為了研究離散事件動態系統表征的行為，同時對經典監控理論做出進一步的抽象，需要在系統的輸出層面上定義一種新的問題，即對系統輸出進行控制，而非對系統內部的原始行為進行控制，稱這種控制問題為DEDS的輸出調節(output regulation,OR).

目前OR在現代控制理論中已經被廣泛研究[12-14]，但關于DEDS的文獻中尚沒有涉及這類問題.在已有的SCT文章中，控制目標都是基于系統內部行為設計的，而非基于輸出行為.例如文獻[7]中，盡管引入了輸出，但考慮的是將事件和輸出組合成擴展的系統行為.因此文獻[7]中的輸出仍和事件停留在同一層次，同樣值得注意的是, 在SCT中人們研究了DEDS的可觀測性[5-6]，并提出了部分可觀的監督控制(partial observed supervisory control,POSC).但POSC和這里提出的OR有所不同.對于前者而言，由于受到傳感器感知精度等因素的制約，監控器獲得的信息不完全，但規約的定義仍是基于系統的原始行為；相較之下，后者則是希望受控系統在信息層面滿足某種特性，其規約定義在系統事件的輸出上，對于監控器沒有特別的限制.

本文將研究系統的OR問題并著重討論輸出的安全性問題，從系統行為和表征的同步關系入手，給出OR監控器的設計方法.接著證明上述方法構造的監控器可以完成OR的控制任務且是最小約束的.最后本文將舉例說明OR問題在實際場景中的建模以及監控器構造算法的有效性.

1 問題定義

1.1 離散事件動態系統建模

考慮以五元組定義的離散事件動態系統

G=(X,Σ,f,Γ,x0),

(1)

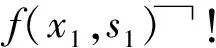
1.2 監督控制

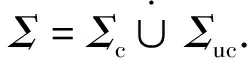
P(ε)=ε,

(2)

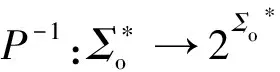
ε∈L(S/G),

[sσ∈L(S/G)]?[sσ∈L(G)]∧[s∈

L(S/G)]∧[σ∈S(P(s))].

(3)

監督控制問題通常都會考慮兩個問題，即存在性問題(existence problem)和綜合問題(synthesis problem).給定一個語言集合K,前者要求找到L(S/G)=K嚴格成立的條件；而后者要求構造出一個監控器，使得受控系統的行為滿足L(S/G)?K.在實際應用中，由于受到各種場景約束，要使L(S/G)=K嚴格成立往往并不容易甚至不可實現，因此研究可以解決綜合問題的監控器構造算法更有實際意義.標準監控問題(standard supervisory control problem，SSCP)的數學定義如下：

問題1(SSCP) 令G為系統自動機，Σc和Σo分別代表可控事件和可觀事件集合.令規約K?L(G)是系統語言的非空子集，設計監控器S:P(L(G))→Γ,使得

1)S是“安全”的，即L(S/G)?K；

2)S是“最小約束”的，即對于任何S′使得L(S′/G)?K,有L(S/G)?L(S′/G).

1.3 OR

本文用原子命題表示事件的輸出，為了描述OR問題，定義事件的輸出函數如下：M:Σ→Δ∪{ε},其中Δ表示原子命題的集合，ε代表空命題.為了定義事件序列的輸出函數, 對上式進行拓展如下：M:Σ*→(Δ∪{ε})*,定義如式(4)所示，其中δ為一個輸出符號.

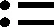
(4)

接著對于給定的語言L,記M(L)為語言輸出的集合：

M(L)={M(s):?s∈L}.

(5)

式(4)形式上類似于自然映射函數的擴展.事實上，輸出函數和自然映射函數可以理解為對系統事件的兩個觀察角度.前者可以認為是從系統使用者角度觀察，涉及到OR問題的控制目標；而后者則是來自系統內部的觀測，監控器看到的就是這部分信息.通過將規約定義在系統輸出上，DEDS的OR問題的數學定義如下：

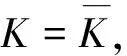
1)S是“輸出安全”的，即M(L(S/G))?K；

2)S是“最小約束”的，即對于任何S′使得M(L(S′/G))?K,有L(S/G)?L(S′/G).

2 輸出調節監控器的設計

經過多年的研究，標準監控問題已經有了成熟的解法[15]，特別是提出了在部分可觀情形下對于多種性質的通用解決方式[16].因此，考慮將OR問題轉化為SSCP，進而構造解決OR問題的監控器.下面介紹的監控器構造方法將會在第3節中給出證明.

考慮輸出規約K和動態系統G=(XG,ΣG,fG,ΓG,x0,G),如果原系統G不滿足M(L(G))?K,就需要構造一個監控器S,使得受控系統S/G在規約K下是輸出安全的，即M(L(S/G))?K.將規約K用自動機的形式表達，記為規約自動機H=(XH,Δ∪{ε},fH,ΓH,x0,H),s.t.L(H)=K.算法1將基于自動機G,H構造一個在其狀態中嵌入了“輸出安全”性質的自動機Gs,進而得到作用于系統事件本身的新規約K′.

為了捕捉自動機中符合輸出安全性質的事件序列，算法需要使用新的組合運算.與傳統的并行組合(parallel composition)運算類似，這種新運算也是基于自動機的同步關系，但研究的對象變成了同一系統的行為及其輸出.相較于并行組合，新運算有兩個特點：一是兩個自動機的事件集不同，確切地說，第二個自動機H的事件集是第一個自動機G的輸出集合；二是運算只完全遍歷第一個自動機G,另一個自動機H跟隨它運行.即在遍歷G時若發生事件e,那么H將轉移至發生M(e)之后的狀態.結合這些特點，稱這種運算為“基于映射的并行組合(mapping-based parallel composition,MBPC)”.

定義1(MBPC)定義關于自動機的二元運算，記作‖M.考慮將離散動態系統建模成自動機G=(XG,ΣG,fG,ΓG,x0,G)；將規約K用自動機的形式表達，記為規約自動機H=(XH,Δ∪{ε},fH,ΓH,x0,H),s.t.L(H)=K.它們的MBPC定義為

G‖MH=(XMP,ΣMP,fMP,ΓMP,x0,MP)，

(6)

其中XMP?XG×XH為自動機G‖MH的狀態集合；組合系統G‖MH的事件集合ΣMP=ΣG,與G的事件集合保持一致；組合系統的轉移函數fMP定義為

fMP((x1,x2),e)=

(7)

因此當組合系統處于狀態xMP=(x1,x2)時，可能發生的事件集合為ΓMP(xMP)=ΓG(x1)；組合系統的初始狀態x0,MP=(x0,G,x0,H)∈XM.

在傳統的并行組合中，兩個系統除了在公共的狀態下運行外，還能在各自獨有的狀態集合中運行.考慮自動機G的運行情況，定義1將[e?ΓG(x1)]∧[M(e)∈ΓH(x2)]涉及的情形列入了“其他”情況.定義1通過系統的行為和表征之間的同步關系，利用規約對系統事件本身進行了標記.基于MBPC運算和規約的轉化，下面提出一種OR監控器的設計算法.

算法1：規約轉化

輸入：

輸出函數M:Σ→Δ∪{ε}

系統自動機G=(XG,ΣG,fG,ΓG,x0,G)

規約自動機H=(XH,Δ∪{ε},fH,ΓH,x0,H)

s.t.L(H)=K?M(L(G))

輸出：

新規約自動機Hs及規約K′ s.t.K′=L(Hs)

步驟1 構造一個標記不安全輸出序列的自動機Ha=(Xa,Δ∪{ε},fa,Γa,x0,a).在規約自動機H的狀態集XH中加入狀態BAD,即Xa=XH∪{BAD},x0,a=x0,H.轉移函數fa定義為

(8)

步驟2 基于MBPC運算，構造Gs=G‖MHa；

步驟3 在Gs中刪除所有含有BAD分量的狀態(形如(xs,BAD))，并刪除所有指向這些狀態的轉移邊.記自動機Gs的剩余部分為Hs,代表組合系統中滿足輸出安全要求的事件序列；

步驟4 返回轉化后的規約K′=L(Hs).

根據算法1的構造過程，可以得到轉化后規約K′的數學描述如下：

K′={s∈L(G):M(s)∈K},

(9)

算法1通過指數復雜度的構造，借助MBPC運算將OR問題轉化為關于系統G和規約K′的SSCP.對事件序列的長度應用數學歸納法容易證明算法1中的兩個自動機Gs和Hs滿足以下性質：

1)L(Gs)=L(G)；

2)L(Hs)?L(G).

基于算法1給出的規約轉化方法，解決OR問題的完整流程如算法2所示：

算法2：輸出調節

輸入：

輸出函數M:Σ→Δ∪{ε}

系統自動機G=(XG,ΣG,fG,ΓG,x0,G)

規約自動機H=(XH,Δ∪{ε},fH,ΓH,x0,H)

s.t.L(H)=K?M(L(G))

輸出：

最小約束輸出安全監控器S*

步驟1 利用算法1推導規約自動機Hs和規約K′；

步驟2 針對規約自動機Hs和系統自動機G應用部分可觀監控器的生成方法[16]得到最小約束輸出安全監控器S*.

3 監控器設計的正確性

上述算法給出了構造OR監控器的方法，完成了從OR問題到SSCP的轉化.本節將會證明監控器構造方法的正確性.

引理1給定系統自動機G,以及轉化前后的規約K和K′,有

M(L(S/G))?K?L(S/G)?K′.

(10)

證明：(?)假設M(L(S/G))?K.根據輸出函數M的定義(式(5))，?s∈L(S/G),

M(s)∈M(L(S/G))?K,

因此s滿足

s∈L(G),M(s)∈K.

根據轉化后規約K′=s∈L(G):M(s)∈K(式(9))有s∈K′,進而有

M(L(S/G))?K?L(S/G)?K′.

(11)

(?)假設L(S/G)?K′.?s∈L(S/G)?K′,由式(9)可知M(s)∈K,進而有

M(L(S/G))?K?L(S/G)?K′.

(12)

綜合式(11)和(12)，M(L(S/G))?K?L(S/G)?K′.證畢.

定理1對于系統G和監控器S*:Σ*→2Σc.S*是使G滿足安全性質L(S*/G)?K′的最小約束的監控器?S*是使G滿足輸出安全性質M(L(S*/G))?K的最小約束監控器.

證明首先證明安全性：根據引理1，L(S*/G)?K′是M(L(S*/G))?K的充要條件.已知S*是使G滿足安全性質L(S*/G)?K′的監控器，那么S*也是能使G滿足輸出安全性質M(L(S*/G))?K的監控器，反之亦然.

接著證明最小約束特性：考慮能夠使L(S*/G)?K′和M(L(S*/G))?K都成立的監控器S*,在輸出安全的規約K下，S*對于系統G是最小約束的，當且僅當在安全性規約K′下，S*對于系統G是最小約束的.

(?)由反證法，假設在安全性規約K′下，S*對于系統G不是最小約束的，即存在一個不同的S′滿足L(S′/G)?K′,且

L(S*/G)?L(S′/G).

(13)

顯然式(13)與“在輸出安全的規約K下，S*對于系統G是最小約束的”相矛盾；

(?)由反證法，假設在輸出安全的規約K下，S*對于系統G不是最小約束的，即存在一個不同的S′滿足M(L(S′/G))?K′,且同樣可以得到式(13)，與“在安全性規約K′下，S*對于系統G是最小約束的”相矛盾.證畢.

4 實例研究

考慮一個檢查機器運行狀態的檢查系統，本節將通過該實例來闡述本文算法的具體應用過程和應用場景.假設需要不定時使用一臺機器，在使用前為了知道機器的狀態是否正常，希望設計一個系統執行以下檢查任務：打開機器時，系統提示機器已開機，然后給出簡短的狀態報告(如“狀態正常”或“需要檢修”)，隨后提示“狀態檢查完成”并結束檢查過程.

設這樣的一個檢查系統G的狀態集為X={x0,x1,x2,x3,x4,x5},事件集為Σ={a1,a2,b},為了敘述方便，不妨假設所有事件都是可控可觀的.當檢查系統管理下的機器啟動時，它處于“開機狀態”，同時檢查系統處于初始狀態x0.當檢查系統處于x0時，期望系統通過事件b聲明機器已開機，并轉移到狀態x1,表明機器處于開機狀態.隨后依據機器的檢查情況，輸出相應的結果信息.如果系統輸出“狀態正常”，則通過事件a1轉移到狀態x2；如果系統輸出“需要檢修”，則通過事件a2轉移到狀態x3.最后系統提示“狀態檢查完成”，通過事件b轉移到狀態x4并結束檢查.值得注意的是，系統在執行檢查任務時，只有上面描述的事件序列可以認為是正常的，由狀態x4接收.各狀態發生的其余事件都會轉移到狀態x5,表示檢查系統出錯了.根據以上描述，系統可以建模為如圖1所示的有限狀態自動機.

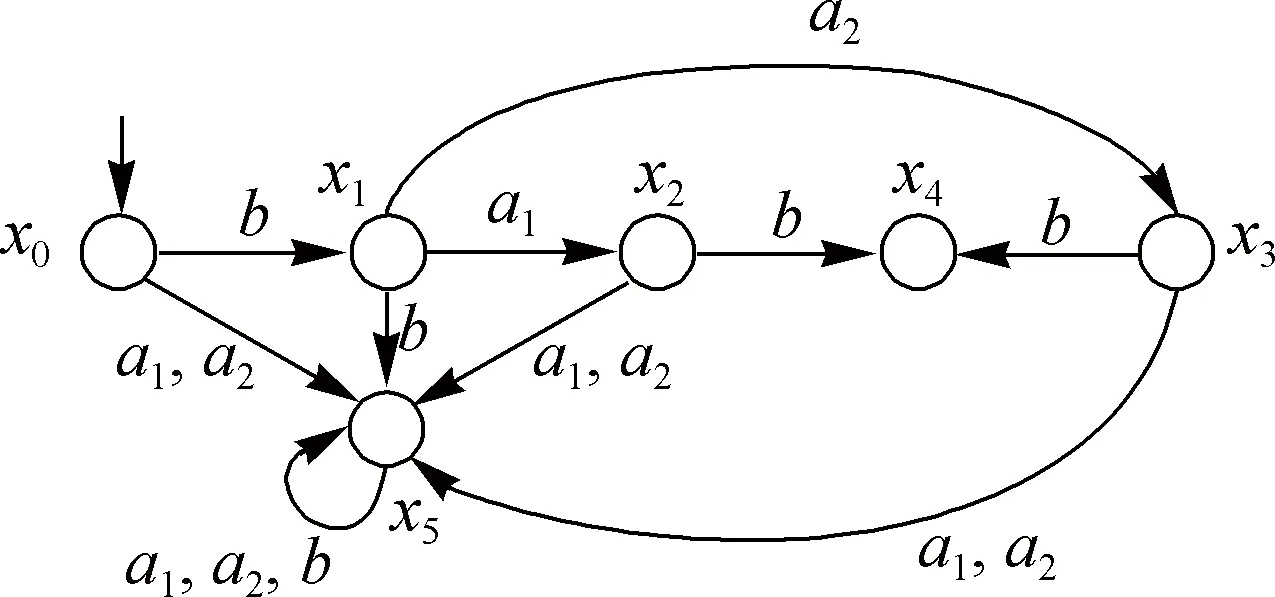
圖1 機器運行狀態檢查系統Fig.1An machine status checking system

前述的檢查系統需要確保在機器開機后依次輸出“初始狀態”、相應的狀態報告和“狀態報告完成”.該任務可以用系統輸出的序列來描述.首先在事件集Σ={a1,a2,b}上定義輸出函數M,M(a1)=a′,M(a2)=a′,M(b)=b′.其中輸出符號b′表示檢查系統輸出指示流程進度的信息，如“初始狀態”或“狀態報告完成”；輸出符號a′表示檢查系統輸出了相應的狀態信息，如“狀態正常”或“需要檢修”.對于檢查任務的描述可以表示為對系統輸出的規約：K={ε,b′,b′a′,b′a′b′}.

因此，針對規約K,本研究希望為系統G設計一個滿足輸出安全性質的最小約束監控器S,即針對規約K和系統G定義OR問題.根據本文算法，給出該問題的求解過程.

如圖2(a)所示，首先將規約K描述為一個自動機H,使得K=L(H).根據算法1，對標記不安全輸出序列的自動機Ha(圖2 (b))和系統自動機G(圖1)應用MBPC組合運算，得到自動機Gs(圖3(a)).最后，刪除所有被標記的狀態以及指向這些狀態的轉移，得到自動機Hs(圖3 (b))，其對應的語言集合K′包含了所有滿足輸出安全性質的事件序列.

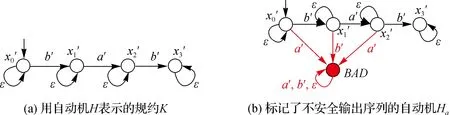
圖2 算法1中步驟1涉及的自動機Fig.2The involved automatons by applying step 1 of algorithm 1

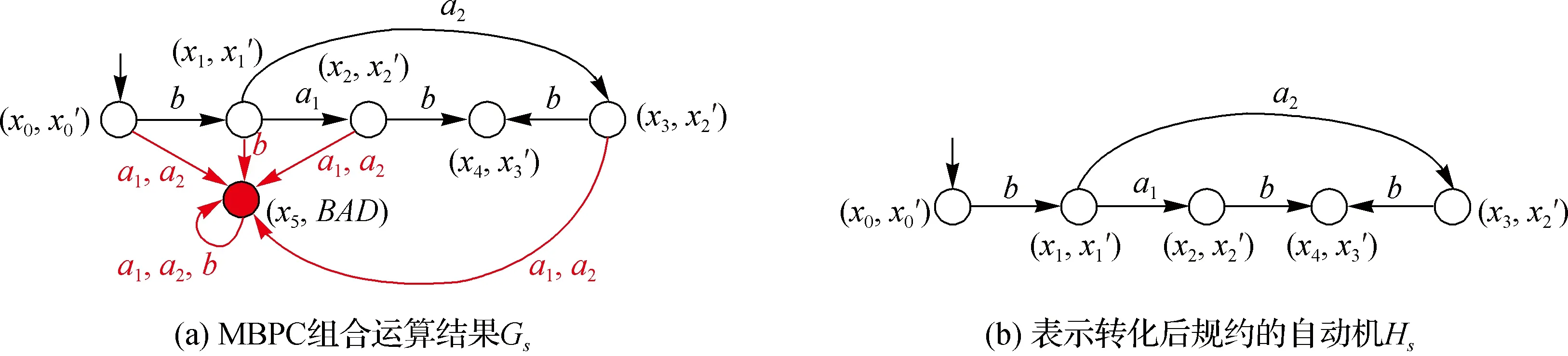
圖3 隱含了控制前后系統行為信息的自動機Gs和HsFig.3The automatons that embed system behaviors before and after supervisory

由于K′={ε,b,ba1,ba2,ba1b,ba2b},包含了系統G中所有滿足規約K的事件序列，從而驗證了算法1的正確性.接著應用算法2中的監控器生成算法，即可得到滿足OR所需的監控器S*.在本例中，S*與如圖3 (b)所示的自動機Hs具有相同的結構.

5 結 論

為了方便實際應用中對離散動態系統表征的研究，本文在DEDS的理論框架下提出了OR問題的概念并給出了嚴格的數學描述.基于系統行為和輸出規約的同步關系，定義了一種新的組合運算以求解OR問題，并在此基礎上實現了由OR問題向SSCP的轉化，通過求解SSCP實現了原OR問題的求解.最后，本文證明了OR監控器設計算法的正確性，并通過機器狀態檢查系統的實例闡述了本文算法的具體應用過程.