奈奎斯特判據在時滯對象自抗擾控制中的應用

金輝宇，倪 剛，蘭維瑤，李智斌

(1.廈門大學航空航天學院，福建廈門361102；2.新華三技術有限公司，浙江杭州310051；3.山東科技大學電氣與自動化工程學院，山東青島266510)

2022年是廈門大學控制科學與工程學科成立50周年，也是奈奎斯特發表文獻[1]90周年.該文提出了基于頻率響應分析反饋系統穩定性的圖形化判據，該判據為控制系統的分析和設計提供了新方法，標志著頻域方法的成熟和古典控制時期的到來.此后，這一判據被稱作奈奎斯特判據，成為古典控制的核心內容，在自動控制的理論研究、工程實踐和教學中發揮著重要作用.而文獻[1]也入選控制理論歷史上最重要的25篇文獻，并因為發表時間而位居第一[2].

然而，20世紀60年代現代控制理論興起后，整個古典控制不再時髦，甚至被誤解為簡單、過時.奈奎斯特判據也就隨之被冷落，在教學和科研中的地位不斷降低.目前，國內通常僅在本科階段學習奈奎斯特判據，研究生階段不再系統講述，轉而強調狀態空間方法.這就導致作為科研主力的研究生們總體上不熟悉奈奎斯特判據，難以用它解決面對的科研問題.而這又進一步加劇了“簡單、過時”的誤解，甚至還要加上“無用”.奈奎斯特判據陷入了“被誤解—不被重視—難以應用—誤解加深”的正反饋，其研究日漸衰微.

與狀態空間方法相比，奈奎斯特判據有其獨特的優勢.它巧妙地平衡了數學嚴謹和工程直觀.它以復變函數理論為基石，充分嚴謹，常常能得到穩定性的充要條件；它以圖形為主要分析手段，足夠直觀，便于工程技術人員接受.它一般不需要繁雜的數學運算，過程簡潔明了，特別適合研究低階單輸入單輸出對象.

為體現奈奎斯特判據的優勢，本文用它研究時滯對象的自抗擾控制(active disturbance rejection control,ADRC).ADRC是韓京清研究員[3-5]提出的一種通用控制技術.它汲取了PID控制的思想精華，具有結構簡單、調參方便、魯棒性好、適用面廣等優點.它以“內擾”來描述對象的不確定性，并將內擾和外擾歸結為總擾動,再構造擴張狀態觀測器(extended state observer,ESO)實時估計總擾動,最后用反饋予以補償,從而實現“自抗擾”.由于統一處理內、外擾，ADRC不依賴對象的數學模型，在克服對象不確定性和抑制外擾方面具有獨特的優勢.21世紀以來，ADRC蓬勃發展，在工業過程、伺服系統、汽車工業和航空航天等領域不斷取得成功應用[6-7].受應用研究的激勵，ADRC的理論研究也日趨活躍，成為當時一個熱點[8-10].

在工業過程領域，由于存在傳輸時滯、容積時滯、測量時滯等因素，被控對象常常是時滯對象.ADRC高度重視時滯對象，發展出無視時滯法、階次提高法、時滯預估法等若干種控制時滯對象的方法，在工程實際中取得了良好的效果[11-12].但時滯對象ADRC的理論研究相對滯后，直到近年才找到若干穩定性條件[13-14].目前，時滯對象ADRC穩定性研究的主要工具是時滯常微分方程穩定性理論，這一時域方法可以得到嚴格、精巧的理論結果，但存在理論艱深、學習困難的缺點.

本文用奈奎斯特判據重新研究了一階時滯對象在ADRC下的穩定性.所研究問題的特點是，對象不穩定或臨界穩定，ADRC中采用降階ESO.這兩點增加了問題的難度，一度被認為難以用傳遞函數方法研究[14].本文先進行框圖化簡，將原問題分母中的超越函數項分離出來，成為時滯對象反饋控制的標準形式.再分情況繪制奈奎斯特圖分析穩定性，得到了與文獻[14]一致的充要條件.這表明，奈奎斯特判據是研究ADRC的有力工具.

1 奈奎斯特判據簡介

考慮圖1(a)所示的反饋控制系統，其中r與y分別參考信號與輸出，G(s)與F(s)分別是前向通道和反饋通道的傳遞函數.該系統的穩定性取決于特征方程

1+G(s)F(s)=0

(1)

根的位置.當且僅當所有的根都在開左半平面(left-half-plane,LHP)時，系統是穩定的.

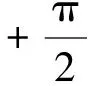
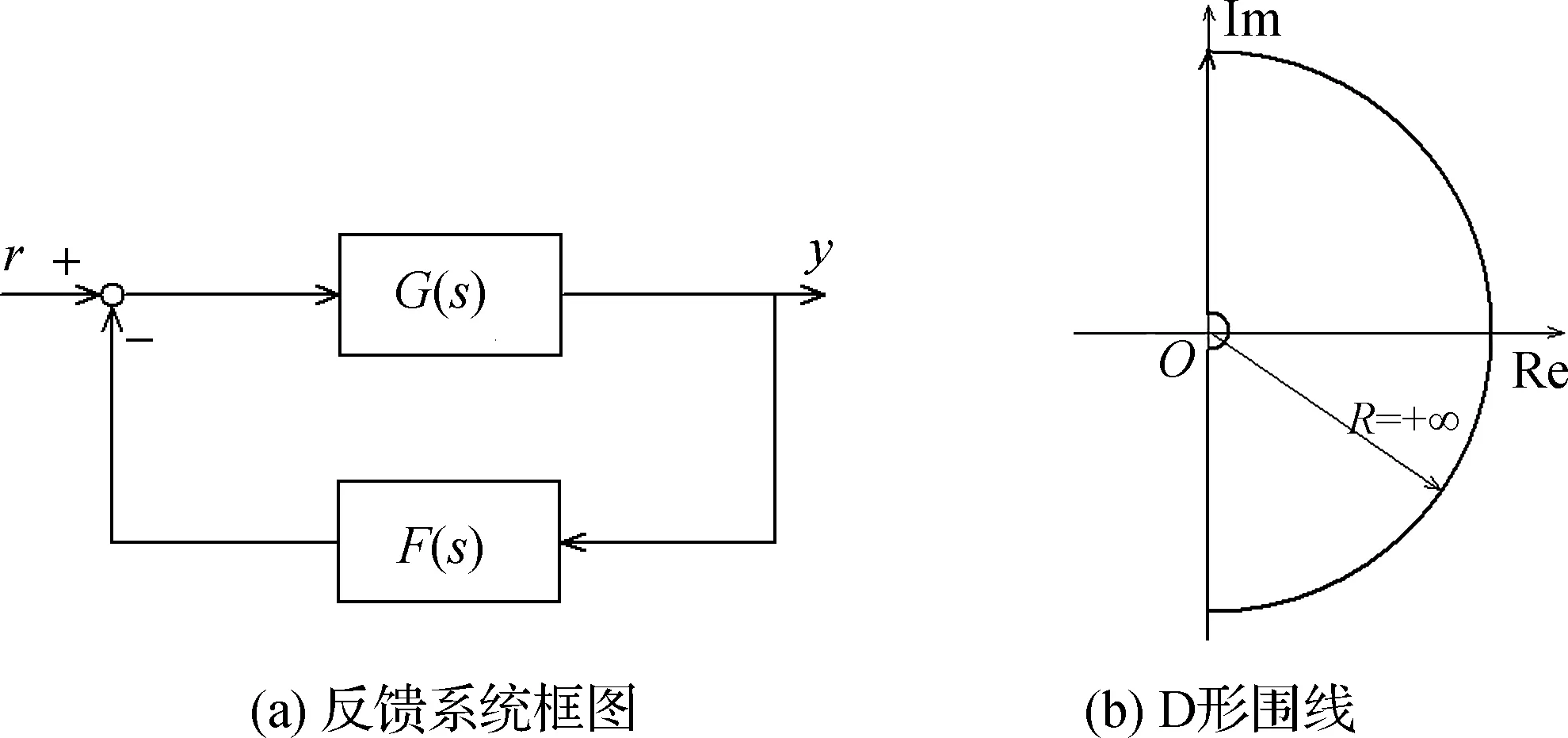
圖1 反饋系統和D形圍線Fig.1Feedback system and D contour

假定奈奎斯特曲線順時針N次包圍點-1+i0，而G(s)F(s)在右半平面有P個極點.奈奎斯特判據斷言，方程(1)的全部根中，不在LHP的根有Z=N+P個.顯然，當且僅當Z=0時，反饋系統穩定.

奈奎斯特判據適用于時滯對象[15].其詳細介紹和繪圖細節可見文獻[16-17].

2 理論結果

2.1 問題描述

設有一階時滯對象

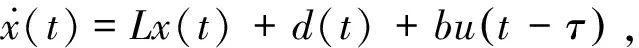
(2)

其中，u和x分別是對象的輸入與輸出，d是外部擾動，常數L，b，τ的數值已知，且滿足L≥0，b,τ>0.控制器設計的目標是跟蹤參考信號r.典型的r是一個階躍信號.

為實現這一目標，文獻[14]設計了降階ESO

(3)

和控制器

(4)

問題是分析由式(2)～(4)組成的一階LADRC系統的穩定性.

注1式(3)被稱作降階ESO的原因是它的微分方程只有一階，而一般針對式(2)設計的ESO為兩階.

2.2 框圖及其簡化

線性自抗擾控制(LADRC)系統(2)～(4)有框圖如圖2[14]所示，其中

(5)

(6)

(7)

由于控制器C(s)的分母是超越函數，其穩定性分析被認為是一個難題.

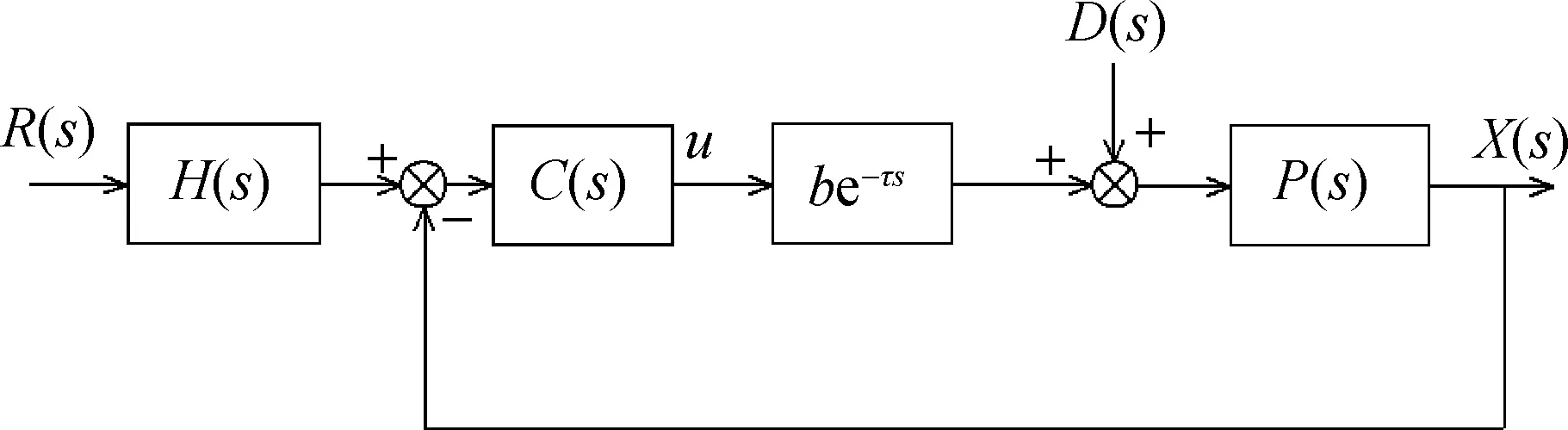
圖2 LADRC系統(2)～(4)的框圖[14]Fig.2Block diagram of LADRC system (2)～(4)[14]

現在化簡圖2.由于外擾不影響線性時不變(linear time-invariant,LTI)系統的穩定性，將D(s)刪去.考慮到圖3所示模塊有傳遞函數

(8)

則圖2可以化簡為圖4(e)，中間過程見圖4(a)～(d).

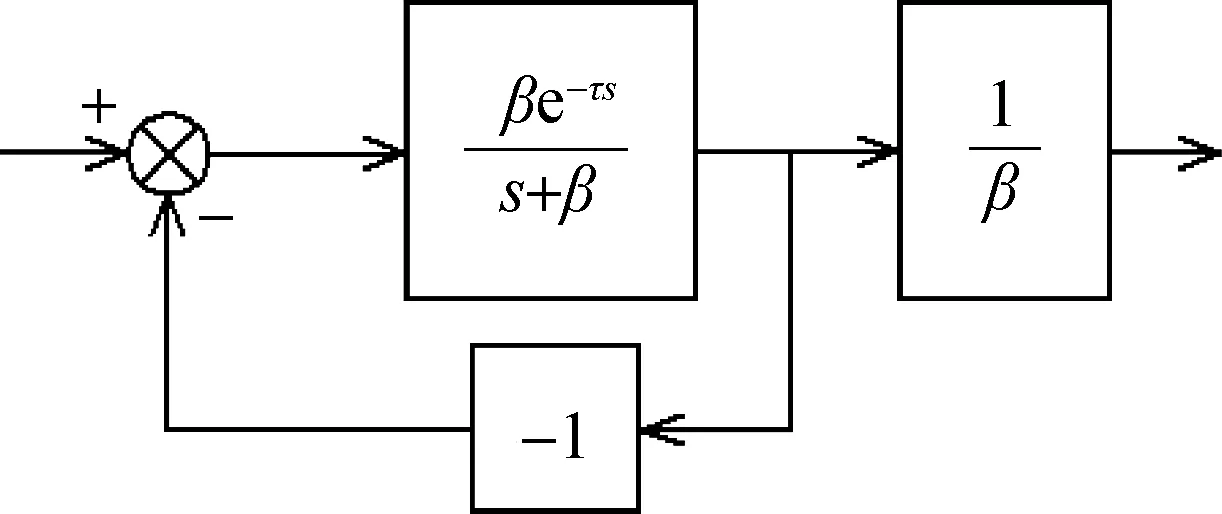
圖3 一個具有傳遞函數(8)的模塊Fig.3A block with transfer function (8)

圖4 化簡圖2結果Fig.4Simplification of Figure 2

2.3 增益穿越頻率

圖4(e)中的反饋回路有傳遞函數

(9)

其特征方程為

(s+β)(s-L)+(ks+kβ+βL)e-τs=0.

(10)

注意到式(10)也是圖2的特征方程，這再次表明圖2和圖4(e)的穩定性相同.

引理1假設k,β>0，考慮式(9)和方程

|W(iω)|=1.

(11)

方程(11)有4個根，其中有且僅有一個正實根

ωc=

(12)

證明方程(11)可以改寫為

兩邊平方后得

ω4+(β2+L2-k2)ω2-(k2β2+2kβ2L)=0.

它有兩個實根ω1,2=±ωc和兩個虛根，其中有且僅有ωc是正實根.

引理1表明，當s從原點出發運動到+i∞的過程中，僅在ωc處穿越單位圓一次.在古典控制中，ωc被稱作增益穿越頻率，它是用奈奎斯特圖分析穩定性時的一個關鍵參數.

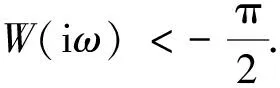
證明由式(9)，有

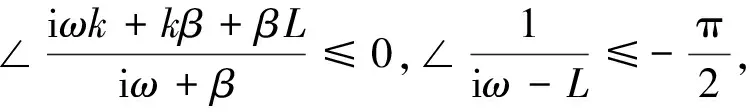
2.4 穩定性條件

現在建立穩定性條件.

定理1考慮由式(2)～(4)組成的一階LADRC系統，假定k+β>L.記時滯上界

τ*=

(13)

該LADRC系統穩定的充要條件是時滯τ<τ*.

證明分別考慮L=0和L>0兩種情況.L=0時，式(9)簡化為

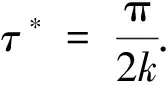
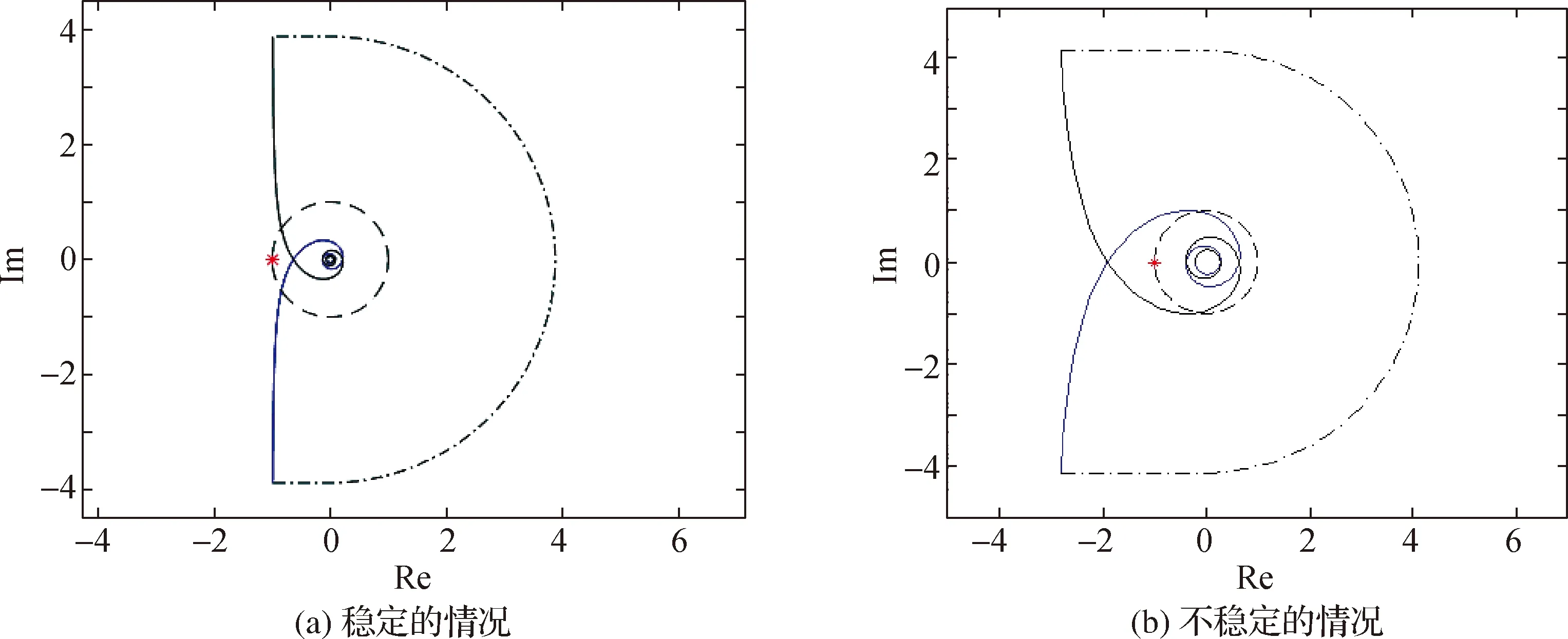
圖5 L=0時W(s)的奈奎斯特圖Fig.5Nyquist diagram of W(s) when L=0

下面證明不包圍點-1的充要條件就是τ<τ*.分析W(s)的奈奎斯特曲線，當ω=0+時，W(iω)在-i∞附近；隨著ω的增加，在ω=ωc處穿越單位圓；此后保持在單位圓內.當且僅當τ<τ*時，有

(14)

由引理2，W(s)的奈奎斯特曲線在第二象限穿入單位圓.此時整個奈奎斯特圖不包圍-1點，如圖5(a)所示，其中藍色實線是s從i0+出發運動到+i∞的曲線，黑色實線是s從-i∞沿負虛軸運動到i0-的曲線，而點劃線大半圓是圖1(b)中D形圍道繞開原點的那一段小半圓生成的.

而當τ≥τ*時，式(14)不成立，系統不是穩定的.圖5(b)是一個不穩定的例子，W(s)的奈奎斯特曲線順時針包圍點-1一次.

當L>0時，W(s)在原點無極點，D形圍道不需要繞開原點.同時W(s)在右半平面有一個極點，由奈奎斯特判據，系統穩定當且僅當奈奎斯特曲線逆時針包圍點-1一次.

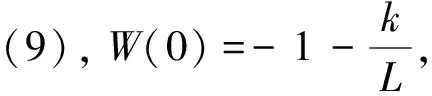
W(iωc)>-π

(15)

時，奈奎斯特曲線在第二象限穿入單位圓，逆時針包圍-1點一次，如圖6(a)所示.其中藍線是從外向內穿入單位圓，而黑線是從內向外穿出單位圓.如果不等式(15)不成立，ADRC系統不是穩定的.圖6(b)是一個不穩定的例子，奈奎斯特曲線順時針包圍點-1一次.

而不等式(15)成立的充要條件就是τ<τ*.因為

-∠(iωc-L)=-π+∠(iωc+L)，

而

∠W(iωc)=∠(ikωc+kβ+βL)-∠(iωc+β)-

∠(iωc-L)-τωc，

于是不等式(15)等價于

τωc<∠(ikωc+kβ+βL)-∠(iωc+β)+

∠(iωc+L).

而由于

∠(ikωc+kβ+βL)-∠(iωc+β)+∠(iωc+L)=

∠(ikωc+kβ+βL)(iωc+L)(-iωc+β)=

ωcτ*，

當且僅當τ<τ*時，不等式(15)成立.

綜合L=0和L>0兩種情況，定理1得證.

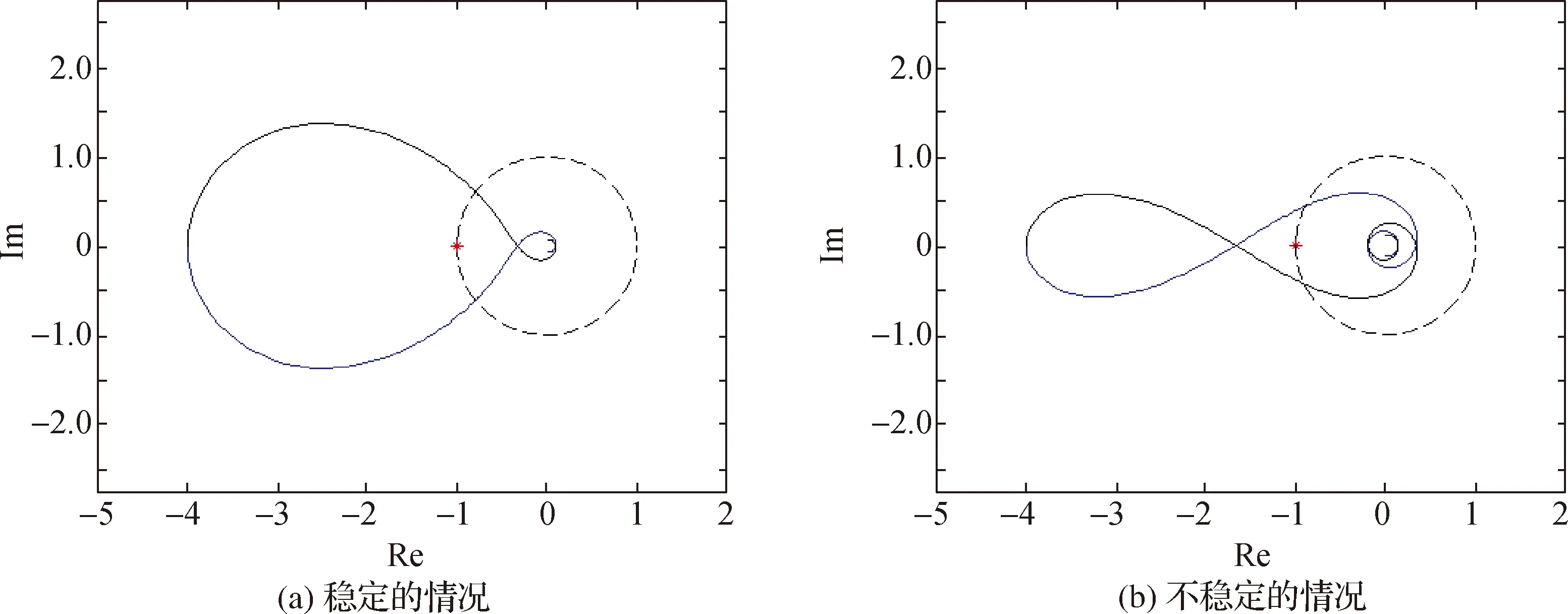
圖6 L>0時W(s)的奈奎斯特圖Fig.6Nyquist diagram of W(s) when L>0

3 討論與算例

3.1 與文獻[14]的比較

定理1得到的時滯上界和文獻[14]一致，這表明了奈奎斯特判據的有效性.但定理1和文獻[14]存在若干差別，在此進行比較.

從方法看，本文的主要方法是奈奎斯特判據，文獻[14]的主要方法是時滯微分方程的穩定性理論.兩種方法都能得到正確的結果，但奈奎斯特判據為自動化背景的研究人員所熟悉，數學專業的未必熟悉；時滯微分方程理論則相反，為數學背景的研究人員所熟悉，但自動化專業的常不熟悉.

從證明過程看，本文需要分別討論L=0和L>0兩種情況，不如文獻[14]數學上簡潔.但從工程的角度，L=0意味著對象臨界穩定且包含一個積分器，而L>0意味著對象不穩定且不包含積分器，兩者的差別明顯而重要.因此，分情況討論在工程上是合理的.

從結果來看，本文沒有對外擾d作假設，而文獻[14]假設d的極限存在且為一個有界常數.這一假設對于穩定性無必要，因為對象和ADRC都是LTI的，整個LADRC系統也是LTI的，而LTI系統的穩定性與外擾無關.這個假設是為了保證d能被完全兌消.

3.2 算例

本節通過兩個算例說明定理1.

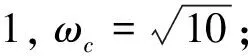
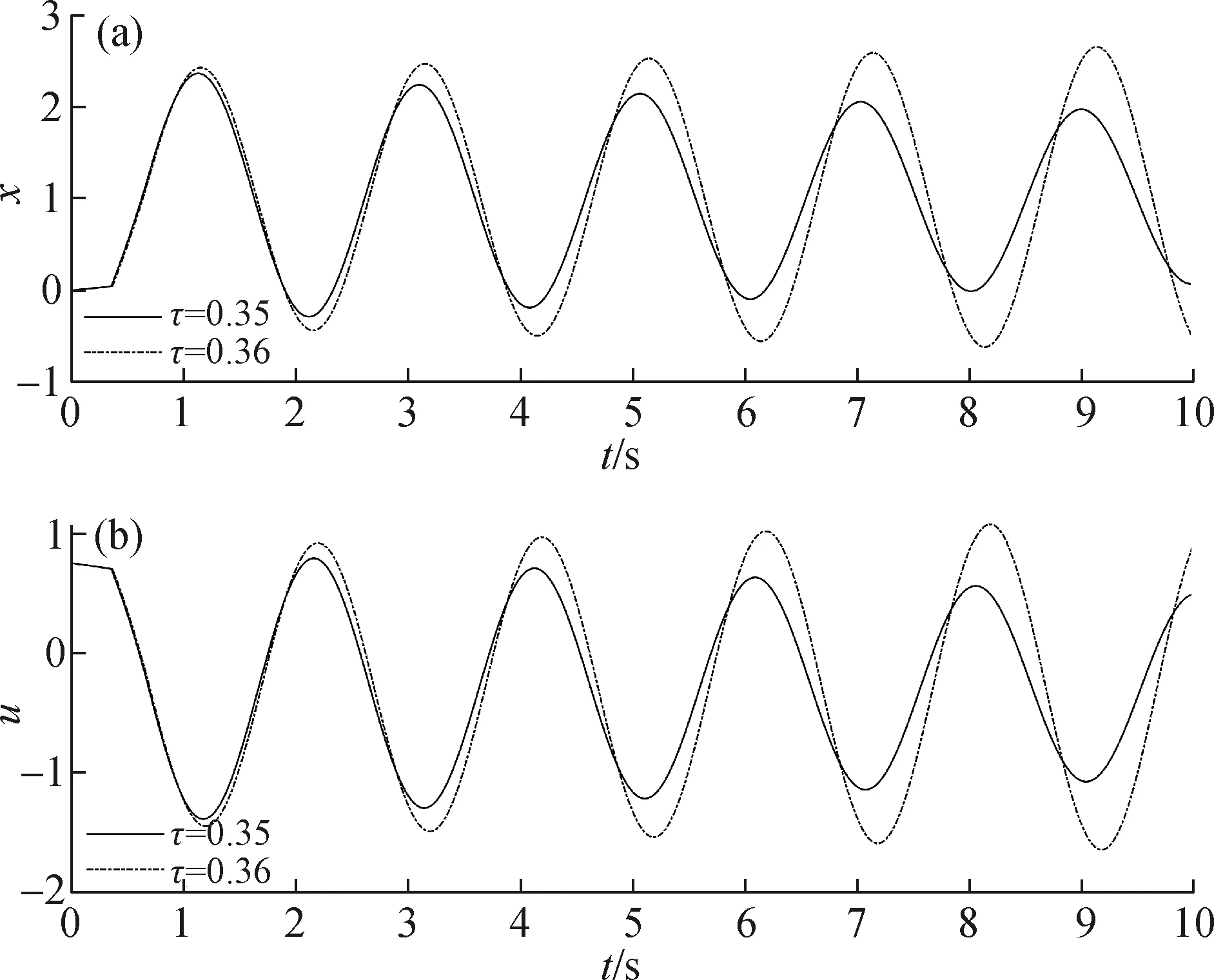
圖7 例1的輸出x(a)和控制u(b)Fig.7The output x(a) and control u(b) of example 1

例2仍取L=1，b=4，β=2，k=3.令τ=0.15，外擾取d1(t)=0.1·1(t)和d2(t)=0.1sin(2t)·1(t).用MATLAB數值求解方程(2)～(4)，結果如圖8.從圖8中可以看到，兩種情況系統都是穩定的，差別在于，d1(t)完全被兌消，而d2(t)沒有被完全兌消，導致x和u在暫態結束以后仍存在振蕩分量.

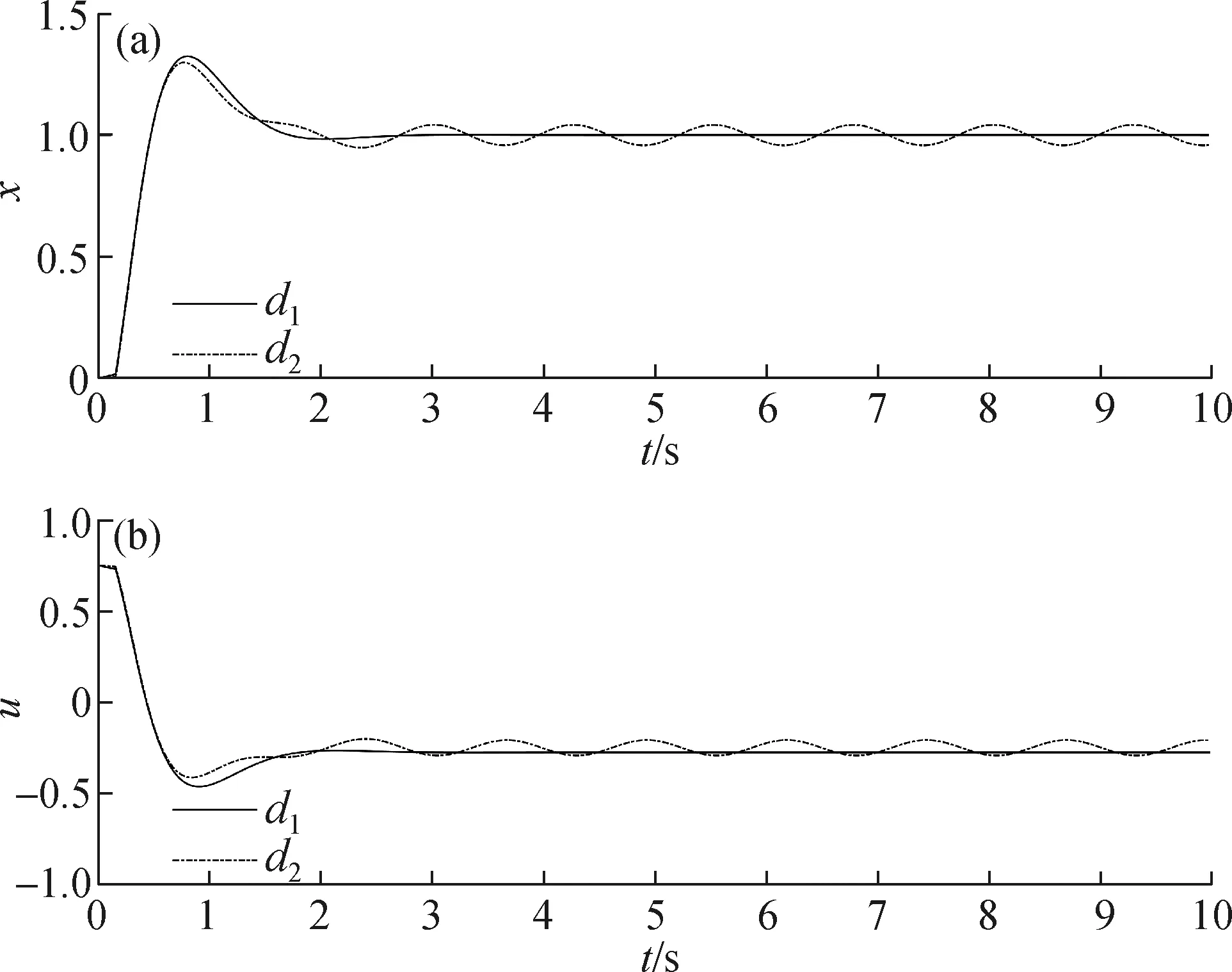
圖8 例2的輸出x(a)和控制u(b)Fig.8The output x(a) and control u(b) of example 2

4 結 論

本文以奈奎斯特判據研究時滯對象自抗擾控制的穩定性，得到了和文獻[14]定理1一致的充要條件，并且放松了對外擾的要求.這表明，奈奎斯特判據并未過時，仍可以在控制理論的前沿研究發揮作用.為更好地發揮其作用，有必要加強奈奎斯特判據和整個古典控制理論的教學，尤其是研究生階段的教學.