地震動輸入界面的選取對地鐵車站地震反應的影響

何 荊，殷 琳，蔡海兵，舒 恩

(1.安徽理工大學 土木建筑學院，安徽 淮南 232001；2.寧波工程學院 建筑與交通工程學院，浙江 寧波 315000)

近年來，關于結構抗震性能的研究取得了廣泛關注[1-2]。研究地鐵車站結構地震反應規(guī)律時，常采用基于有限元建模的時程分析法。建模時，需在半無限空間中截取有限范圍土體，其中底部邊界的選取問題也應關注[3]。關于地下結構有限元分析模型的底部邊界問題，國家相關規(guī)范[4]給出建議：底部邊界應從距地下結構距離3倍結構單邊最大尺寸處至基巖面，該建議給出底邊界取值的范圍較寬，可操作性不強。為此，上海市規(guī)范[5]在此基礎上建議底部邊界取至地表向下70m處。上海地區(qū)軟土層厚度普遍在200m以上，按上海市規(guī)范建議，計算模型土層厚度約取為實際土層總厚度的1/3，如此將導致計算模型的動力特性與實際情況有較大差別，因此可能會導致一定的計算誤差，關于誤差變化情況目前少有研究。基于此，本文以上海典型深厚軟弱場地地鐵車站作為算例，分析底部邊界選取不同對地鐵車站地震響應影響。

1 基本運動方程及求解

對地下結構-土層系統(tǒng)建立運動方程時，可采用粘滯阻尼或復數(shù)阻尼。當采用粘滯阻尼時，土層-地下結構進行地震反應計算的運動方程如式(1)所示。

(1)

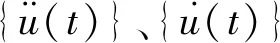
對式(1)的求解，可選用模態(tài)疊加法或逐步積分法。當計算系統(tǒng)為土層-地下結構這種基頻低、模態(tài)密集、自由度規(guī)模大的系統(tǒng)時，不適合用模態(tài)疊加法，因為這類計算系統(tǒng)需要較多的模態(tài)參與才能得到精度滿意的計算結果，不方便計算。若選用逐步積分，又會因阻尼矩陣的構造帶來計算誤差[6]。

采用復數(shù)阻尼可以避免粘滯阻尼帶來的問題。采用復數(shù)阻尼時，土層-地下結構進行地震反應計算的運動方程如式(2)所示。

(2)

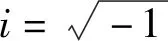
(-ω2[M]+2iη[K]+[K]){u(ω)}={peff(ω)}

(3)

在復數(shù)域內求出{u(ω)}，如式(4)所示。

(4)

若計算系統(tǒng)由多種不同阻尼比的材料組成，還可以將式(4)變形為式(5)。

(5)

其中，ηj為第j種材料滯后阻尼系數(shù)，[Kj]為第j種材料的剛度矩陣。

將式(4)作Fourier逆變換可得時域內位移的解{u(t)}。由式(4)可知，相比于采用粘滯阻尼，采用復數(shù)阻尼的優(yōu)點如下：①僅需求解復代數(shù)方程，對計算機硬件要求不高；②阻尼比不隨激振頻率的變化而變化，不會因阻尼矩陣的構造帶來誤差；③對不同的材料可以設置不同的阻尼比，不需要對系統(tǒng)的阻尼比進行等效。復數(shù)阻尼的不足之處在于對非線性問題，只能進行等效線性計算，不方便進行真非線性分析。

2 算例

本文選取2個不同場地條件下的地鐵車站為算例。研究不同地震動輸入對地鐵車站地震反應的影響。算例1為上海市人民廣場場地中的典型地鐵車站結構，不考慮土體的非線性性質。算例2為上海市軌道交通13號線某站點場地條件下的地鐵車站結構，土體非線性采用等效線性化計算。

算例1：上海市人民廣場場地土層深約230m，共有18層土，各層土物理性質如表1所示。地鐵車站埋深2m，為雙層雙柱島式鋼筋混凝土結構。車站斷面總寬為20m，高11.54m，中跨寬6m，側跨寬6.3m，上層高3.5m，下層高6.4m，中柱間距7.8m。頂板、底板、側墻彈性模量為3.0×1010pa，密度為2.5×103kg/m3。因中柱具有不連續(xù)性，采用二維平面應變模型時，應將中柱材料參數(shù)進行等效[7-9]。等效后中柱彈性模量為3.08×109pa，密度為3.2×102kg/m3。建立阻尼模型時，整個計算模型的阻尼比近似取為0.05[10]。地鐵車站橫截面形式如圖1所示。

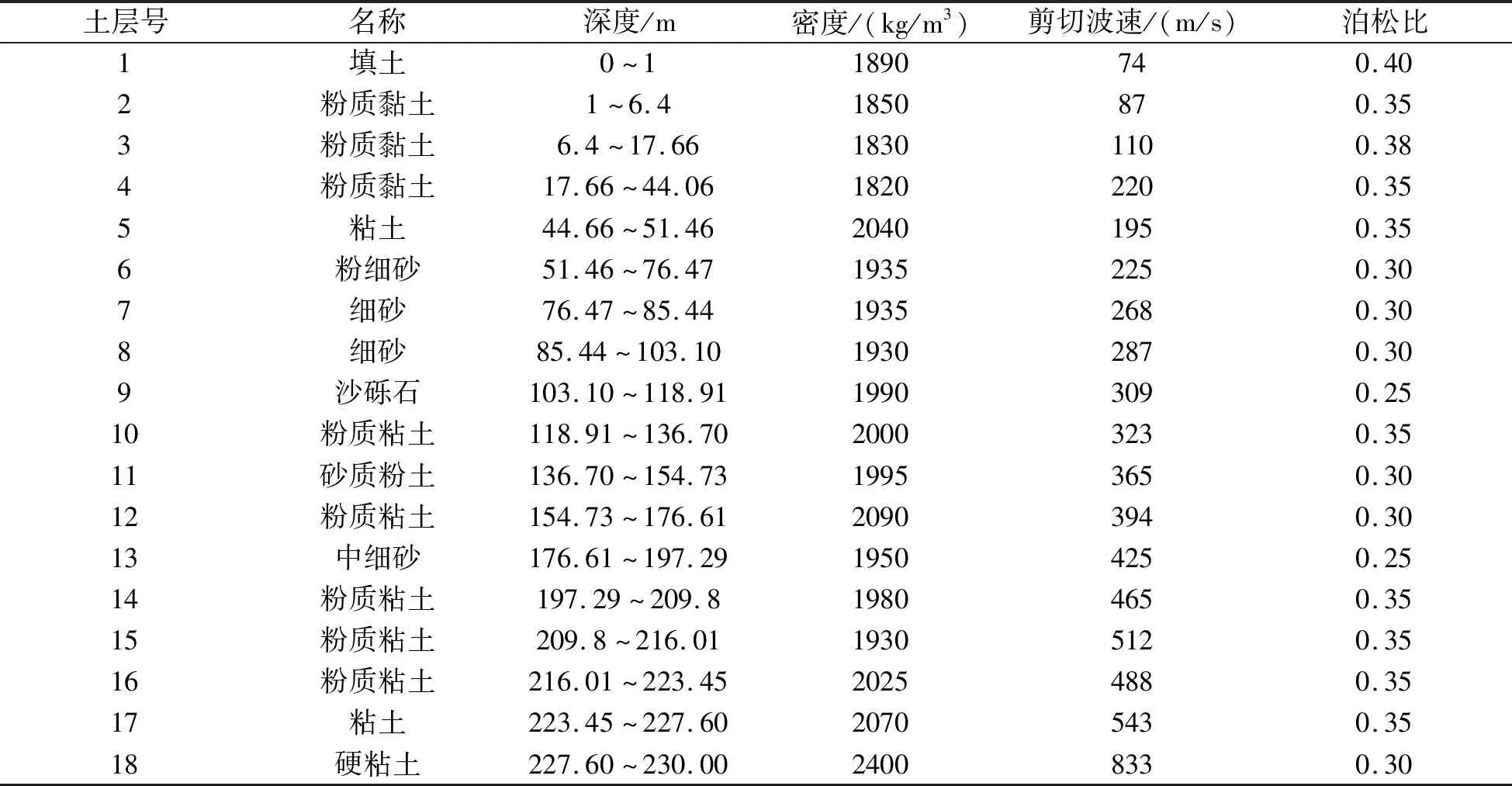
表1 算例1場地土性質物理參數(shù)

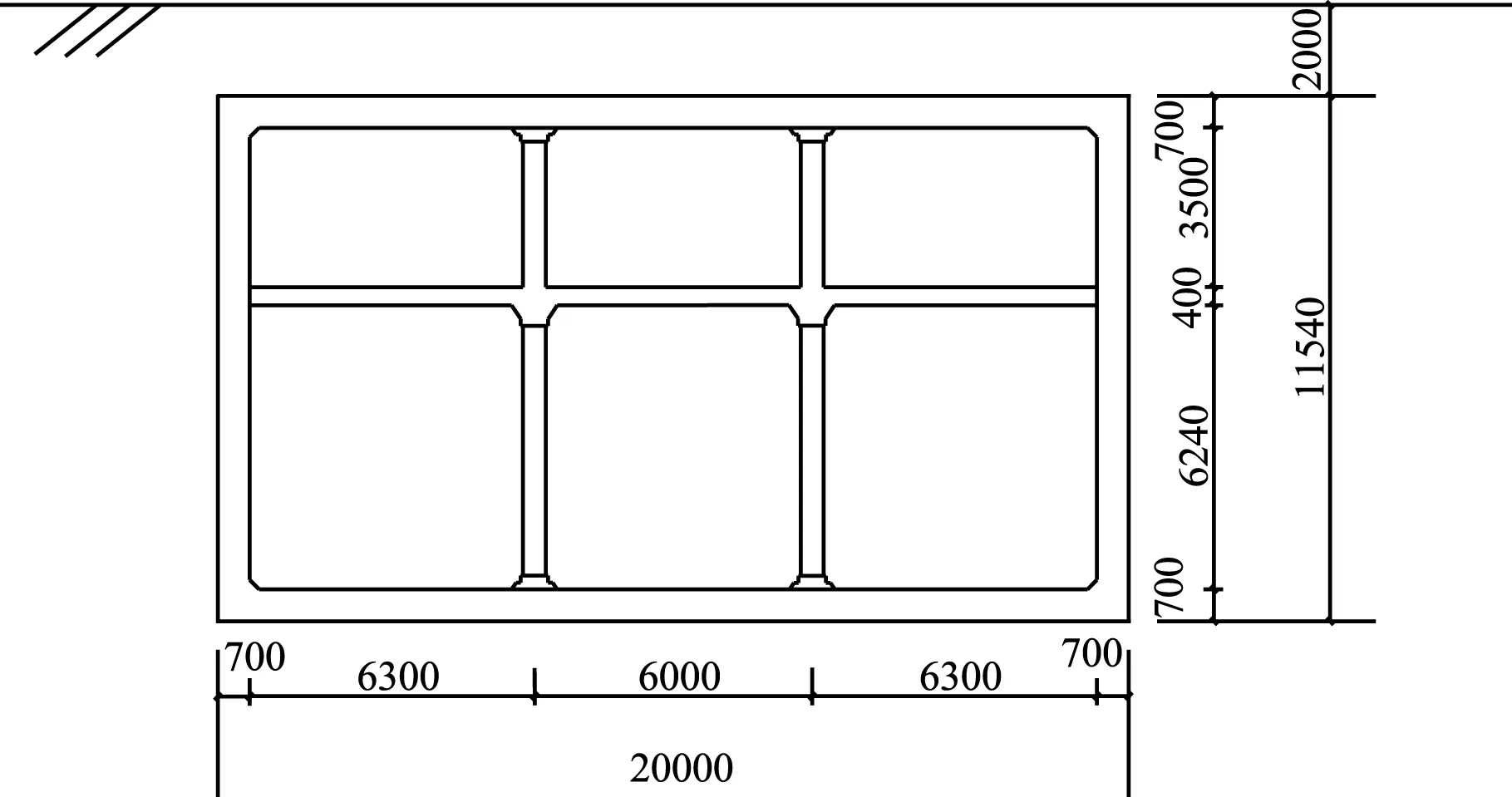
圖1 地鐵車站截面圖

采用二維平面應變模型時，為減少側向邊界帶來的計算誤差，根據樓夢麟等人[11]研究計算模型的水平向寬度取1150m。土體部分用四邊形等參元進行離散，單元豎向網格尺寸控制依據為25Hz正弦波所對應波長的1/16～1/8，橫向網格尺寸取為豎向的2～3倍。約束土體側邊豎向自由度，放松水平向自由度，使之成為側移邊界。約束模型底部結點所有自由度，使其成為固定邊界。地下結構用梁單元離散，不考慮土體與地下結構間的脫離與滑移。

采用三種地震波作為激勵地震動，即汶川波、Kobe波、人工波1。其加速度時程及其FFT譜如圖2所示。

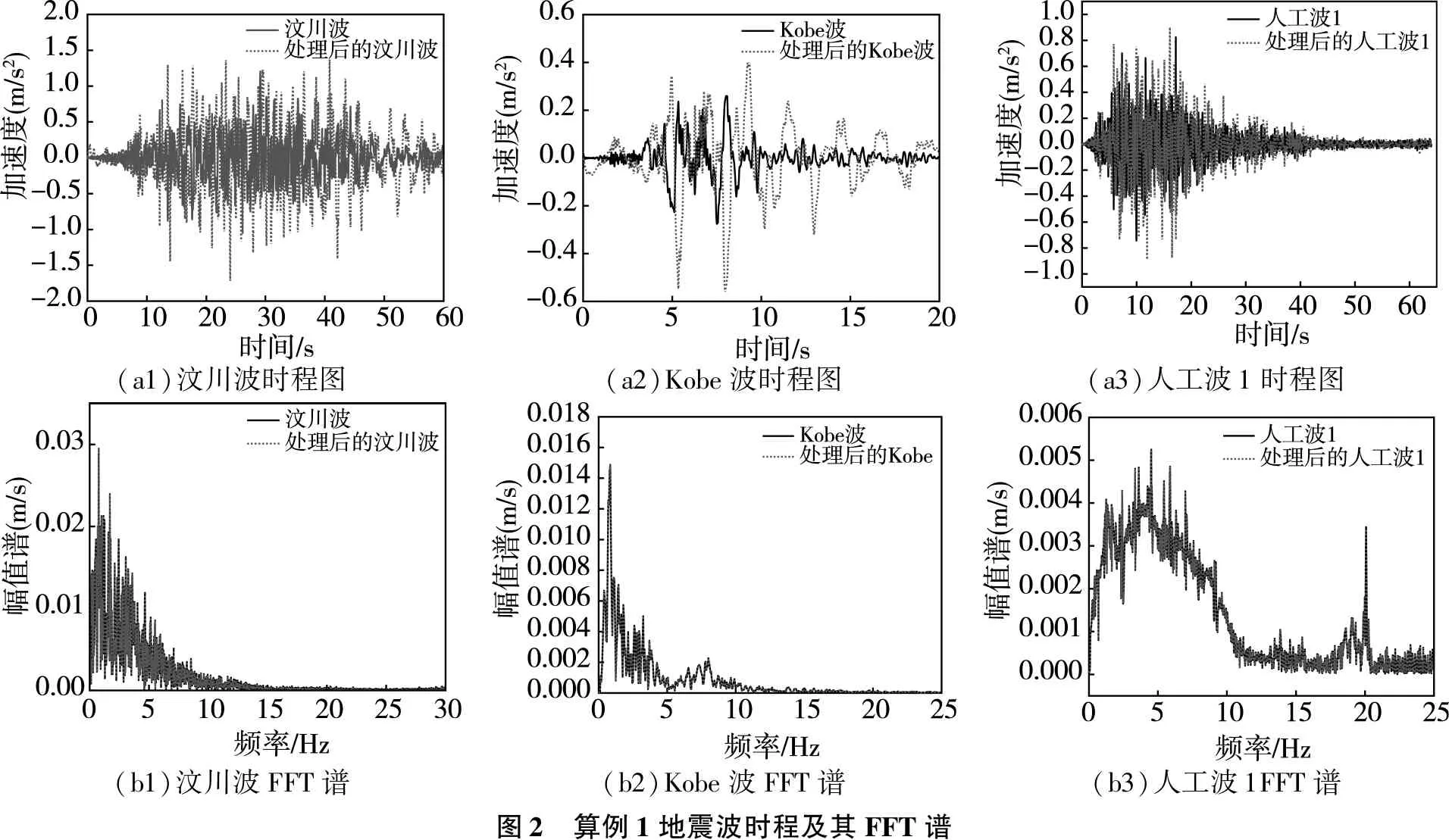
(a1)汶川波時程圖(a2)Kobe波時程圖(a3)人工波1時程圖(b1)汶川波FFT譜(b2)Kobe波FFT譜(b3)人工波1FFT譜圖2 算例1地震波時程及其FFT譜

為評價不同地震動輸入面對地鐵車站結構地震反應的影響，建立兩個計算模型。模型1的地震動輸入面取至基巖面處，稱之為界面1，以汶川波、kobe波、人工波1作為激勵地震動，相應工況為1a；模型2地震動輸入面為離地表70m處的假設基巖面，本文稱之為界面2，以處理后的汶川波、kobe波、人工波1作為激勵地震動，工況稱之為1b。模型1和模型2的計算簡圖如圖3所示。

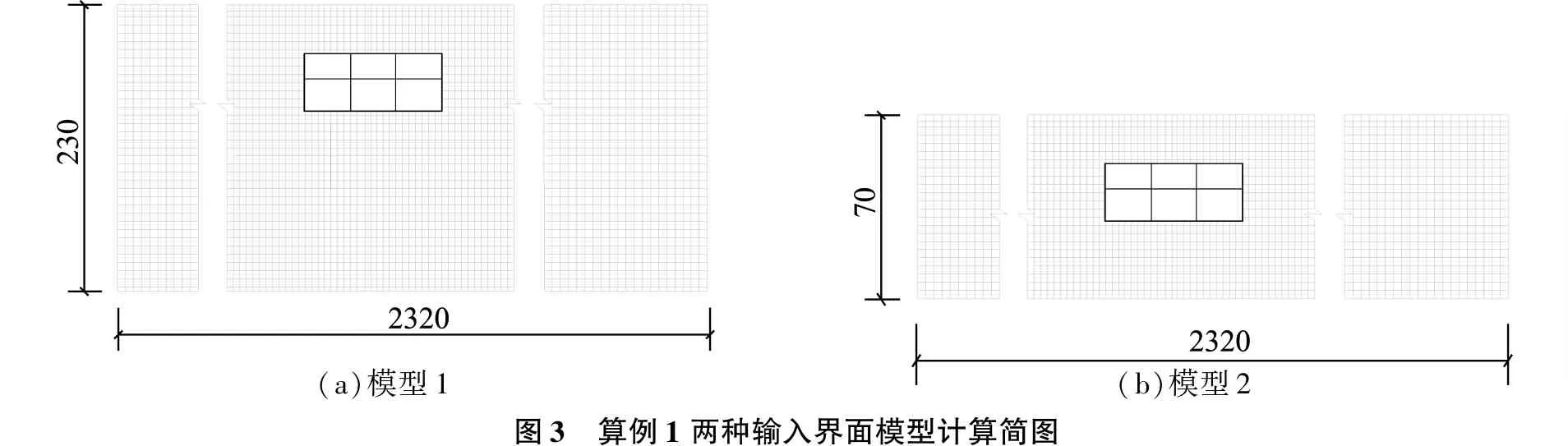
(a)模型1(b)模型2圖3 算例1兩種輸入界面模型計算簡圖

大量震害結果表明[12-13]地下結構中柱頂、中柱底、側壁頂、側壁底是薄弱環(huán)節(jié)，故提取這四個部位在最不利情況下的內力進行分析，其內力峰值情況如表2所示。

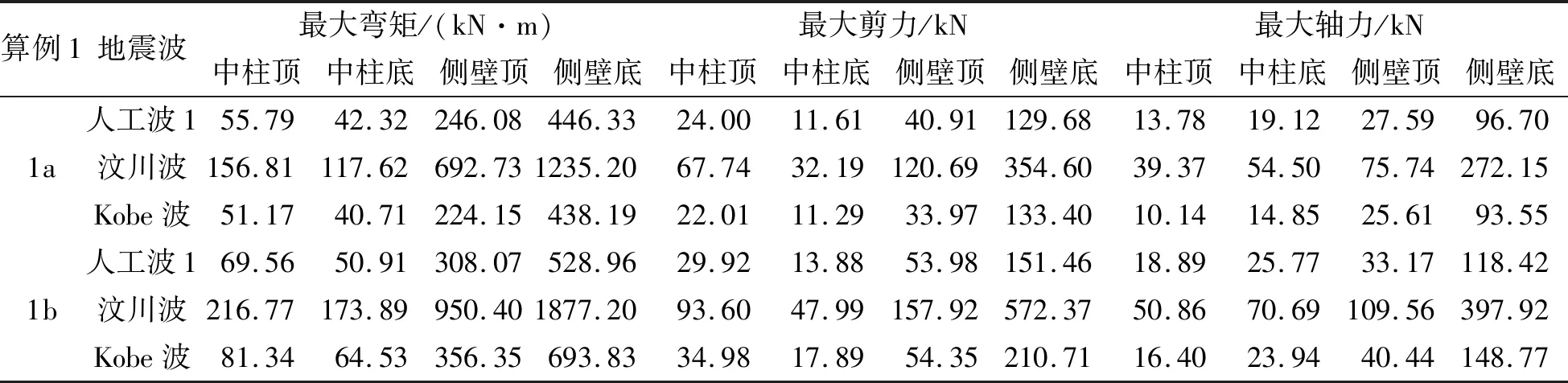
表2 算例1地下結構地震反應峰值

由表2可知，算例1a、1b在三種不同地震波激勵下，側壁的剪力、彎矩、軸力值均大于中柱，算例1a四個部位相應內力均小于算例1b。其中，汶川波激勵下，地鐵車站四個部位的內力明顯大于其他兩個地震波，側壁底的最大彎矩值更是達到了1235.20kN·m。為充分分析模擬時基巖面選取不同對計算結果的影響，利用誤差計算公式(6)。

η=100%×(Rb-Ra)/Ra

(6)

分別計算算例1中工況1a和工況1b的誤差值，對相應誤差值進行分析。式(6)中Ra為1a對應內力值，Rb為1b內力值，誤差情況如圖4所示。

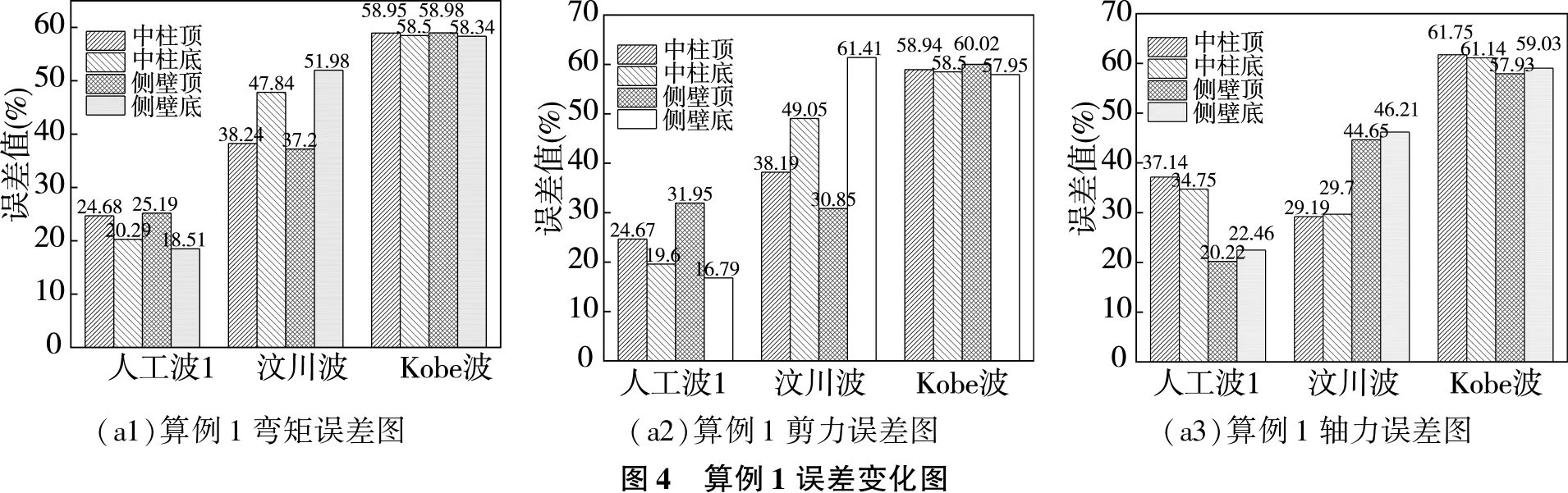
(a1)算例1彎矩誤差圖(a2)算例1剪力誤差圖(a3)算例1軸力誤差圖圖4 算例1誤差變化圖

由圖4可知，在人工波1和Kobe波激勵下，四個部位誤差變化情況類似。除側壁頂軸力誤差略小于側壁底外，其余頂部內力誤差均大于底部。與人工波1相比，Kobe波四個部位的彎矩、剪力誤差值比較接近，都在58%左右。汶川波激勵下，誤差變化情況與Kobe波和人工波1不同。汶川波激勵下，頂部彎矩、剪力、軸力誤差均小于底部，其中側壁底剪力誤差高達61.41%，相較側壁頂增長近31%。綜合來看，算例1在不同波的激勵下，誤差值均值為正，內力誤差范圍在16.79%～61.75%。

算例2：上海軌道交通13號線某車站場地土層厚327.6m，分18層土，各層土的厚度和物理性質如表3所示，各層土的非線性性質如表4所示。該車站結構尺寸和材料物理性質與算例1一致。本算例的模型計算范圍、有限單元的選擇、網格尺寸的確定，邊界條件的設置均與算例1相一致。

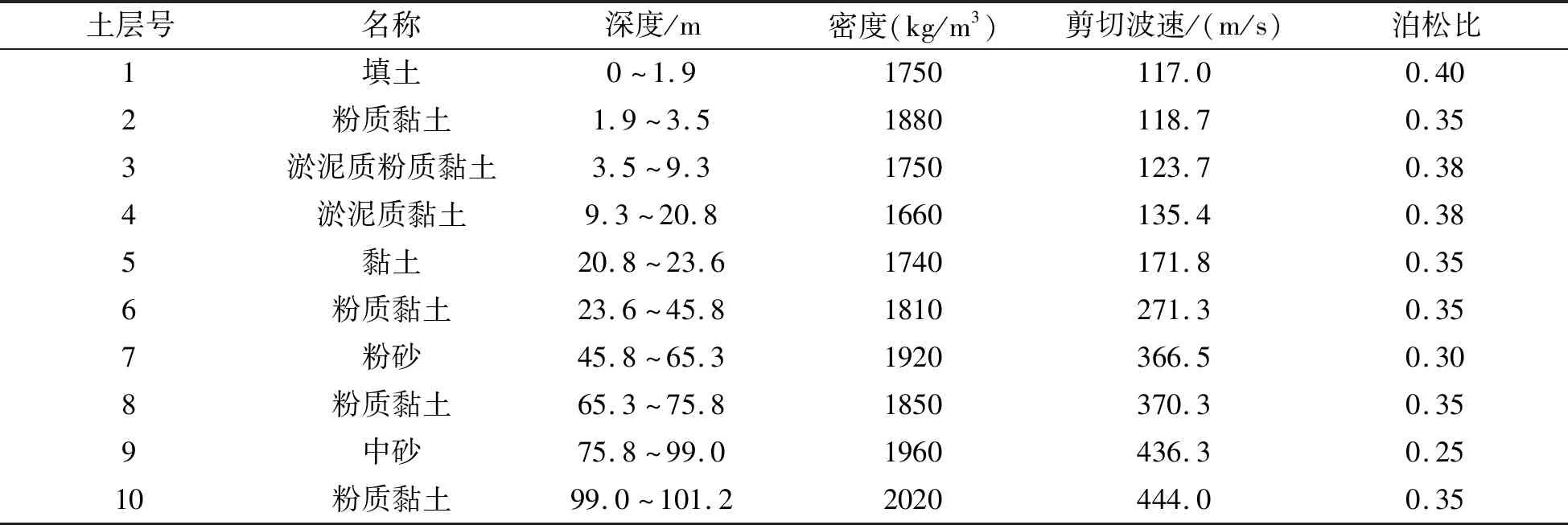
表3 算例2場地土性質物理參數(shù)

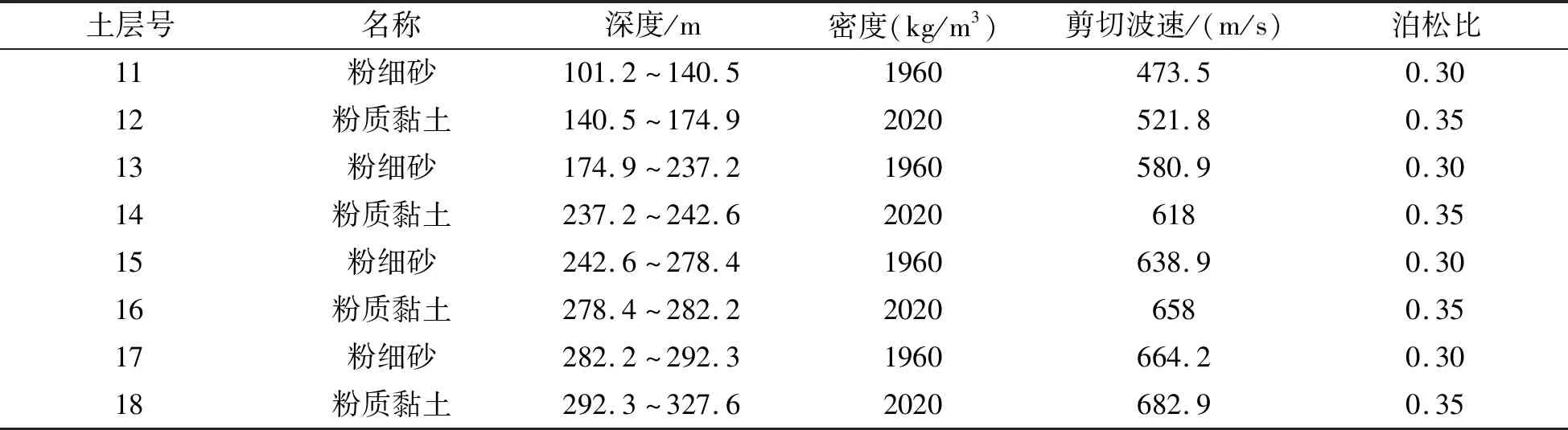
續(xù)表3

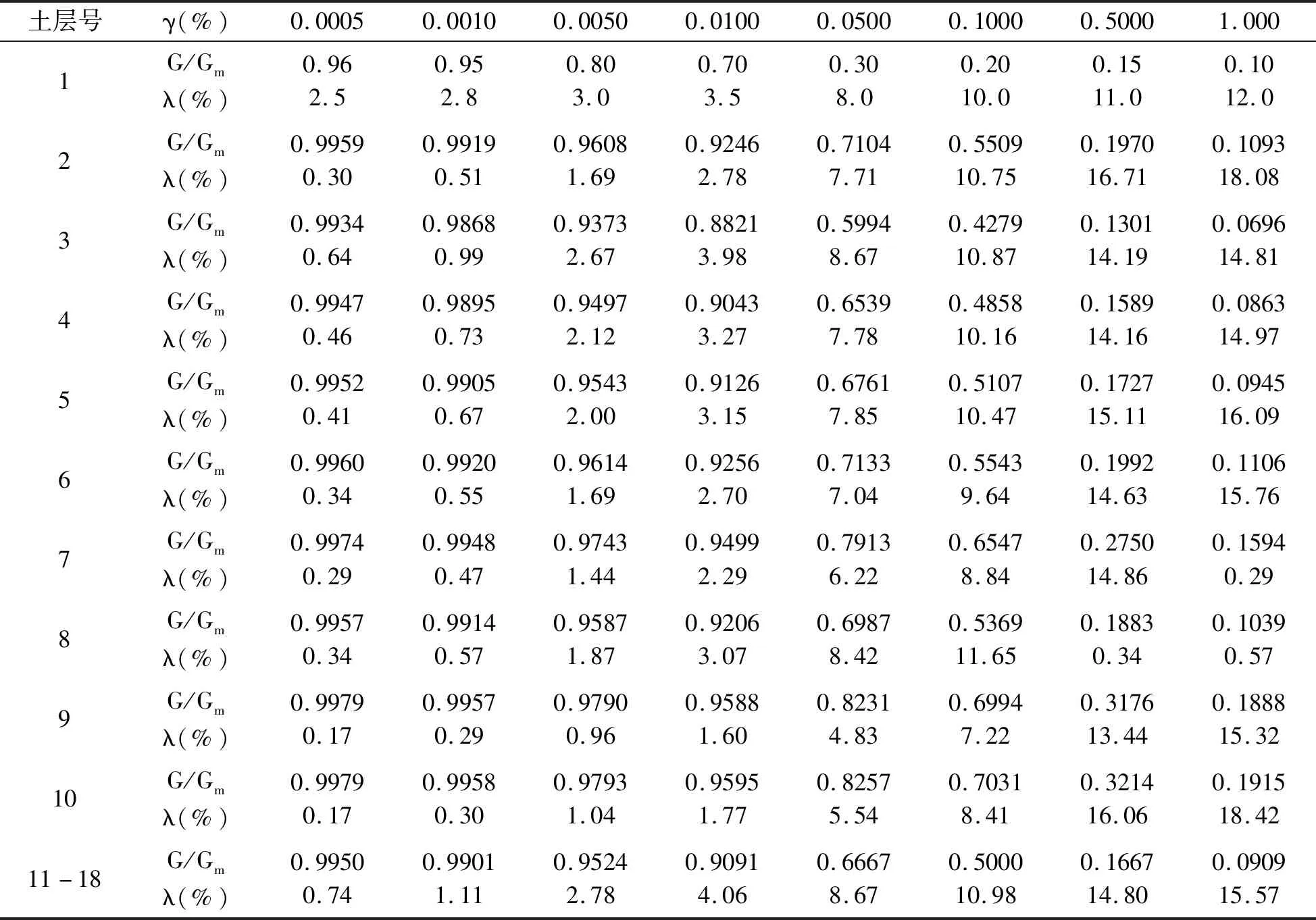
表4 土體動剪切模量和阻尼比值

算例2采用安評資料生成的人工波2作為激勵地震動，其加速度時程及其FFT譜如圖5所示。

(a)人工波2時程圖

建立2個計算模型，模型1的地震動輸入面為離地表327.6m的真實基巖面處，以人工波2作為激勵地震動，相應的工況稱之為2a；模型2的地震動輸入面取為離地表70m處的假設基巖面，以處理后的人工波2作為激勵地震動，相應的工況稱之為工況2b。模型1和模型2的計算簡圖如圖6所示。

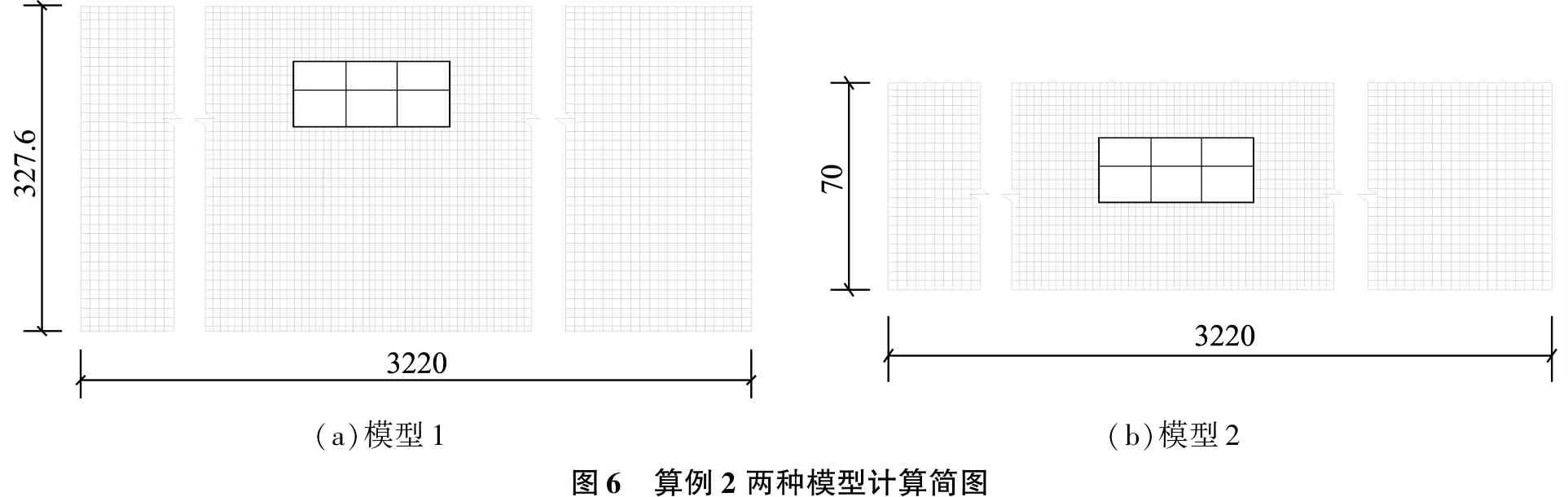
(a)模型1(b)模型2圖6 算例2兩種模型計算簡圖

中柱頂、中柱底、側壁頂、側壁底內力峰值情況如表5所示。利用誤差計算公式(6)，計算算例2誤差值，對其誤差值進行分析。其中，Ra為2a對應內力值Rb為2b內力值，誤差情況如表5所示。

表5 算例2地下結構地震反應峰值和誤差

由表5可得，在人工波2的激勵下，中柱頂彎矩、剪力均大于中柱底，軸力略小于中柱底。側壁頂各個內力均小于側壁底。算例2b四個部位的內力值都大于算例2a。彎矩、剪力、軸力誤差變化情況與算例1中汶川波激勵時相似，頂部誤差小于底部誤差，誤差值在29.19%～61.41%之間。

3 結論

(1)地鐵車站基巖邊界取至地表往下70m處，各重要部位內力均大于取至實際基巖面深度，會產生較大誤差。故有限元模擬時應選用真實基巖面作為地震動輸入面。

(2)不同地震波激勵下，基巖邊界取至地表往下70m左右處與取至實際基巖面處相比，產生誤差大小不同。其中Kobe波激勵下產生誤差最大，各重要部位誤差大小也較為集中，均在58%～62%之間。

(3)在汶川波和人工波2激勵下，中柱頂、側壁頂?shù)膹澗亍⒓袅Α⑤S力分別小于中柱底、側壁底。在人工波1和Kobe波激勵下，除側壁頂軸力小于側壁底外，中柱頂和側壁頂?shù)膹澗亍⒓袅笥谥兄缀蛡缺诘住?/p>