基于LSTM(長(zhǎng)短期記憶)網(wǎng)絡(luò)的城市軌道交通列車(chē)停站精度預(yù)測(cè)*

謝嘉琦 鄒喜華 汪小勇 畢文峰 華志辰

(1.西南交通大學(xué)信息科學(xué)與技術(shù)學(xué)院， 610031， 成都； 2.卡斯柯信號(hào)有限公司， 200072， 上海∥第一作者， 碩士研究生)

0 引言

許多城市軌道交通線路采用了全自動(dòng)運(yùn)行系統(tǒng)。全自動(dòng)運(yùn)行系統(tǒng)不僅可以保障列車(chē)的運(yùn)行安全，有效提升線路的折返效率，還可以減輕運(yùn)維作業(yè)的工作量[1]。與傳統(tǒng)有人駕駛城市軌道交通線路相比，列車(chē)進(jìn)站自動(dòng)停車(chē)功能是全自動(dòng)運(yùn)行線路的優(yōu)勢(shì)之一。在列車(chē)進(jìn)站自動(dòng)停車(chē)的過(guò)程中，停車(chē)精度是衡量列車(chē)是否停準(zhǔn)的一個(gè)重要指標(biāo)。

影響列車(chē)停車(chē)精度的因素主要有以下幾點(diǎn)：首先是列車(chē)自身因素，ATO(列車(chē)自動(dòng)運(yùn)行)系統(tǒng)會(huì)給空氣制動(dòng)系統(tǒng)設(shè)定一個(gè)預(yù)壓力，以提高空氣制動(dòng)的響應(yīng)速度，從而導(dǎo)致列車(chē)實(shí)際的制動(dòng)力偏高[2]；其次，考慮到故障-安全原則，ATO會(huì)對(duì)制動(dòng)系統(tǒng)設(shè)定一個(gè)空氣制動(dòng)余量，這個(gè)余量會(huì)導(dǎo)致列車(chē)實(shí)際制動(dòng)力略大于所需值；再次，在線路方面，某些車(chē)站的線路曲線半徑過(guò)小，以及露天線路天氣的影響、各站點(diǎn)應(yīng)答器的安裝差異、站臺(tái)門(mén)的對(duì)位差異等因素，都會(huì)在一定程度上影響列車(chē)的停車(chē)精度[3]。

國(guó)內(nèi)外關(guān)于ATO模式下列車(chē)停車(chē)控制的研究主要集中在兩大方面：優(yōu)化控制算法和機(jī)器學(xué)習(xí)方法。由于城市軌道交通線路投入運(yùn)營(yíng)后基本不會(huì)更改列車(chē)運(yùn)行的控制算法，且停車(chē)過(guò)程的建模較為困難，因此，優(yōu)化控制算法在城市軌道交通中的適用性不強(qiáng)。在機(jī)器學(xué)習(xí)方法的相關(guān)研究中，文獻(xiàn)[4]對(duì)停車(chē)過(guò)程中列車(chē)的速度、位置等信息進(jìn)行建模，對(duì)比了CNN(卷積神經(jīng)網(wǎng)絡(luò))和DNN(全連接神經(jīng)網(wǎng)絡(luò))兩種算法的優(yōu)劣。文獻(xiàn)[5]利用多種數(shù)據(jù)挖掘算法(如Ridge回歸、RBF(徑向基函數(shù))神經(jīng)網(wǎng)絡(luò)等)構(gòu)建了列車(chē)停車(chē)精度的預(yù)測(cè)程序。文獻(xiàn)[6]采用了機(jī)器學(xué)習(xí)中的Boosting回歸算法對(duì)列車(chē)停車(chē)精度進(jìn)行了回歸預(yù)測(cè)。

城市軌道交通的運(yùn)維人員通過(guò)收集長(zhǎng)期的列車(chē)停車(chē)精度數(shù)據(jù)，根據(jù)數(shù)據(jù)每日的變化趨勢(shì)，手動(dòng)對(duì)列車(chē)停車(chē)的追蹤目標(biāo)點(diǎn)進(jìn)行調(diào)整。這種做法工作量大、效率低下，嚴(yán)重影響了生產(chǎn)效率。因此，迫切需要找到一種有效的方法，通過(guò)對(duì)歷史大數(shù)據(jù)進(jìn)行分析，找出隱藏其中的數(shù)據(jù)規(guī)律，為列車(chē)進(jìn)站自動(dòng)停車(chē)精度提供輔助預(yù)測(cè)，用以指導(dǎo)車(chē)輛運(yùn)維人員進(jìn)行參數(shù)配置。

本文提出一種列車(chē)進(jìn)站自動(dòng)停車(chē)精度的預(yù)測(cè)方法。該方法采用Weibull分布參數(shù)擬合每期的停車(chē)精度分布，得到分布擬合結(jié)果后，構(gòu)建LSTM(長(zhǎng)短期記憶)網(wǎng)絡(luò)算法模型。在此基礎(chǔ)上，采用成都某地鐵線路列車(chē)的歷史數(shù)據(jù)對(duì)模型進(jìn)行訓(xùn)練和驗(yàn)證，對(duì)預(yù)測(cè)模型的分布參數(shù)進(jìn)行回歸預(yù)測(cè)。在工程應(yīng)用上，城市軌道交通車(chē)輛運(yùn)維人員將列車(chē)實(shí)時(shí)的停車(chē)精度數(shù)據(jù)序列輸入到模型后，模型將自動(dòng)預(yù)測(cè)列車(chē)在下一個(gè)車(chē)站的停車(chē)精度，運(yùn)維人員從而可以通過(guò)手動(dòng)移動(dòng)列車(chē)的追蹤目標(biāo)點(diǎn)來(lái)確保列車(chē)精確停車(chē)。

1 列車(chē)進(jìn)站自動(dòng)停車(chē)精度預(yù)測(cè)分析與擬合

1.1 列車(chē)進(jìn)站自動(dòng)停車(chē)精度預(yù)測(cè)分析的算法框架

圖1為列車(chē)進(jìn)站自動(dòng)停車(chē)精度預(yù)測(cè)分析的主要流程。該流程主要包括以下5個(gè)步驟。

步驟1：數(shù)據(jù)清洗。運(yùn)維人員獲得現(xiàn)場(chǎng)停車(chē)日志后，提取出列車(chē)停車(chē)精度的記錄信息，并對(duì)其中無(wú)效的數(shù)據(jù)予以去除。

步驟2：對(duì)列車(chē)停車(chē)精度數(shù)據(jù)進(jìn)行預(yù)處理。根據(jù)城市軌道交通一線員工的工作經(jīng)驗(yàn)，將列車(chē)停車(chē)精度的歷史數(shù)據(jù)以1 d為1個(gè)統(tǒng)計(jì)周期進(jìn)行預(yù)處理(如數(shù)據(jù)清洗、數(shù)據(jù)轉(zhuǎn)換等)。

步驟3：采用Weibull最小極值分布法和Weibull最大極值分布法對(duì)每個(gè)統(tǒng)計(jì)周期的數(shù)據(jù)進(jìn)行擬合，得到對(duì)應(yīng)的分布參數(shù)；對(duì)比分析這兩種分布的擬合度，得到對(duì)應(yīng)參數(shù)的時(shí)間序列。

步驟4：構(gòu)建LSTM預(yù)測(cè)模型。在已獲得的時(shí)間序列基礎(chǔ)上，采用LSTM網(wǎng)絡(luò)算法構(gòu)建列車(chē)進(jìn)站自動(dòng)停車(chē)精度的LSTM預(yù)測(cè)模型；對(duì)模型進(jìn)行驗(yàn)證評(píng)估，并對(duì)下一個(gè)統(tǒng)計(jì)周期的分布參數(shù)進(jìn)行預(yù)測(cè)。

步驟5：預(yù)測(cè)模型的應(yīng)用。通過(guò)預(yù)測(cè)獲得的下一個(gè)統(tǒng)計(jì)周期的分布參數(shù)，綜合評(píng)估下一個(gè)統(tǒng)計(jì)周期列車(chē)停車(chē)精度調(diào)整的偏差值。

圖1 列車(chē)進(jìn)站自動(dòng)停車(chē)精度預(yù)測(cè)分析算法框架

1.2 列車(chē)停車(chē)精度分布擬合

目前，主要采用兩種方法對(duì)Weibull分布進(jìn)行參數(shù)擬合：最大似然估計(jì)法和矩估計(jì)法。本文經(jīng)過(guò)大量的實(shí)踐驗(yàn)證后，采用簡(jiǎn)單有效的最大似然估計(jì)法對(duì)Weibull分布進(jìn)行參數(shù)估計(jì)。Weibull分布的最大似然函數(shù)為：

L(x1,x2,x3,…,xi,α,β)=

(1)

式中：

由于車(chē)次數(shù)一般少于車(chē)組數(shù)，因此，首先需將車(chē)組號(hào)對(duì)應(yīng)的最佳匹配車(chē)次進(jìn)行補(bǔ)全，依次加1，作為車(chē)組號(hào)最佳匹配車(chē)次參考。車(chē)組Ti與車(chē)次Fj的匹配度Cij的計(jì)算公式如下：

L——Weibull分布的最大似然函數(shù)；

x1,x2,x3,…,xi——各維度的數(shù)據(jù)值，i為停車(chē)精度的維度；

α、β——Weibull分布擬合參數(shù)；

n——自然數(shù)序列。

式(1)兩邊取對(duì)數(shù)，可得：

lnL(x1,x1,x1,…,x1;α,β)=

(2)

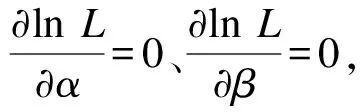
(3)

求解上式(3)，即求得α和β。

2 LSTM預(yù)測(cè)模型的實(shí)例驗(yàn)證與結(jié)果分析

2.1 數(shù)據(jù)的處理及擬合

從圖2 a)可以看出，這些數(shù)據(jù)在整體分布上具有正態(tài)分布的特點(diǎn)。采用Alpha分布、Weibull分布(包括Weibull最大極值分布、Weibull最小極值分布)及Laplace分布對(duì)數(shù)據(jù)進(jìn)行擬合，得到的擬合結(jié)果如圖2 b)所示。其中，Weibull分布擬合效果最好。因此，本文采用Weibull分布對(duì)該線列車(chē)后續(xù)每一個(gè)統(tǒng)計(jì)周期的數(shù)據(jù)進(jìn)行擬合并分析。

a) 整體停車(chē)精度分布

b) 分布擬合

根據(jù)列車(chē)運(yùn)行計(jì)劃，該列車(chē)在1 d內(nèi)停靠站臺(tái)的次數(shù)為534次。該列車(chē)的歷史數(shù)據(jù)統(tǒng)計(jì)了256 d，以1 d為1個(gè)統(tǒng)計(jì)周期，則將歷史數(shù)據(jù)劃分為256期，即有256個(gè)數(shù)據(jù)樣本。對(duì)每1期數(shù)據(jù)采用Weibull分布進(jìn)行擬合，可得到Weibull分布擬合尺度參數(shù)和形狀參數(shù)的時(shí)間序列。由于數(shù)據(jù)過(guò)多，為便于展示，本文僅列出第1期、第50期、第100期、第150期、第200期及第250期的數(shù)據(jù)樣本，以及這些樣本對(duì)應(yīng)的分布參數(shù)，如表1所示。

2.2 構(gòu)建LSTM預(yù)測(cè)模型

利用多層網(wǎng)絡(luò)搜索法，尋找LSTM網(wǎng)絡(luò)最佳擬合參數(shù)的三維圖，3個(gè)維度分別是窗口長(zhǎng)度l、學(xué)習(xí)率η、狀態(tài)大小Sstate。對(duì)這3個(gè)維度進(jìn)行量綱一化處理，可以得到最佳的擬合參數(shù)分別為：l=3，η=0.012 84，Sstate=4.573 5。

表1 列車(chē)停車(chē)精度的Weibull分布參數(shù)

圖3是測(cè)試集上對(duì)Weibull最小極值分布和Weibull最大極值分布的形狀參數(shù)和尺度參數(shù)的預(yù)測(cè)結(jié)果。這兩個(gè)參數(shù)均具有周期化波動(dòng)的趨勢(shì)，傳統(tǒng)的機(jī)器學(xué)習(xí)方法不適用于處理這類(lèi)預(yù)測(cè)問(wèn)題。并且，本文所研究的數(shù)據(jù)是一維的時(shí)間序列，而在時(shí)間序列的預(yù)測(cè)方面，基于RNN(循環(huán)神經(jīng)網(wǎng)絡(luò))的LSTM網(wǎng)絡(luò)有較好的效果，因此，構(gòu)建基于RNN的LSTM預(yù)測(cè)模型。由圖3可看出，量綱一化后得到的列車(chē)停車(chē)精度分布預(yù)測(cè)效果與各統(tǒng)計(jì)周期下的現(xiàn)場(chǎng)原始數(shù)據(jù)分布基本吻合。由此可以得出結(jié)論：LSTM預(yù)測(cè)模型能夠較好地捕捉尺度參數(shù)和形狀參數(shù)的變化趨勢(shì)，并可準(zhǔn)確地預(yù)測(cè)后續(xù)統(tǒng)計(jì)周期的參數(shù)值。

a) 最小極值尺度參數(shù)預(yù)測(cè)

b) 最小極值形狀參數(shù)預(yù)測(cè)

c) 最大極值尺度參數(shù)預(yù)測(cè)

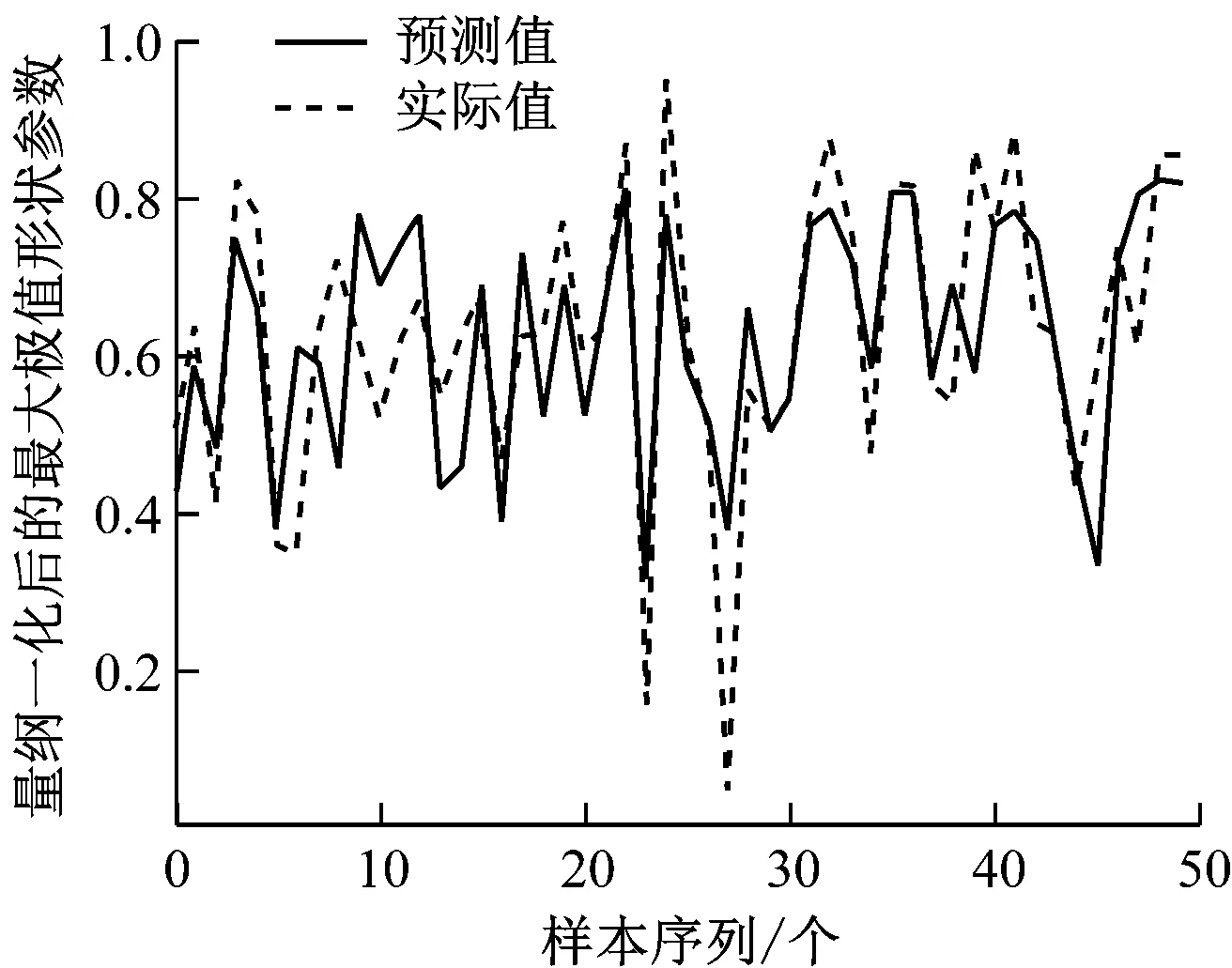
d) 最大極值形狀參數(shù)預(yù)測(cè)

圖4為L(zhǎng)STM預(yù)測(cè)模型最小極值尺度參數(shù)的均方誤差值ERMS，以及預(yù)測(cè)值分布和實(shí)際值分布的相似度MS的計(jì)算結(jié)果。由圖4可知，隨著訓(xùn)練輪數(shù)的增加，ERMS大為降低，在100輪左右ERMS下降到0.043 7并趨于穩(wěn)定。這說(shuō)明模型訓(xùn)練比較充分，可滿(mǎn)足統(tǒng)計(jì)學(xué)角度對(duì)ERMS的要求。形狀參數(shù)和尺度參數(shù)時(shí)間序列的預(yù)測(cè)效果較好，從而驗(yàn)證了LSTM預(yù)測(cè)模型的有效性。

從分布相似性的角度看，預(yù)測(cè)值分布和實(shí)際值分布的相似性均值EAR為0.942 6，且每一個(gè)統(tǒng)計(jì)周期的MS均大于0.9。這說(shuō)明LSTM預(yù)測(cè)模型具有較好的普遍適用性和有效性。

a) ERMS隨訓(xùn)練次數(shù)的變化情況

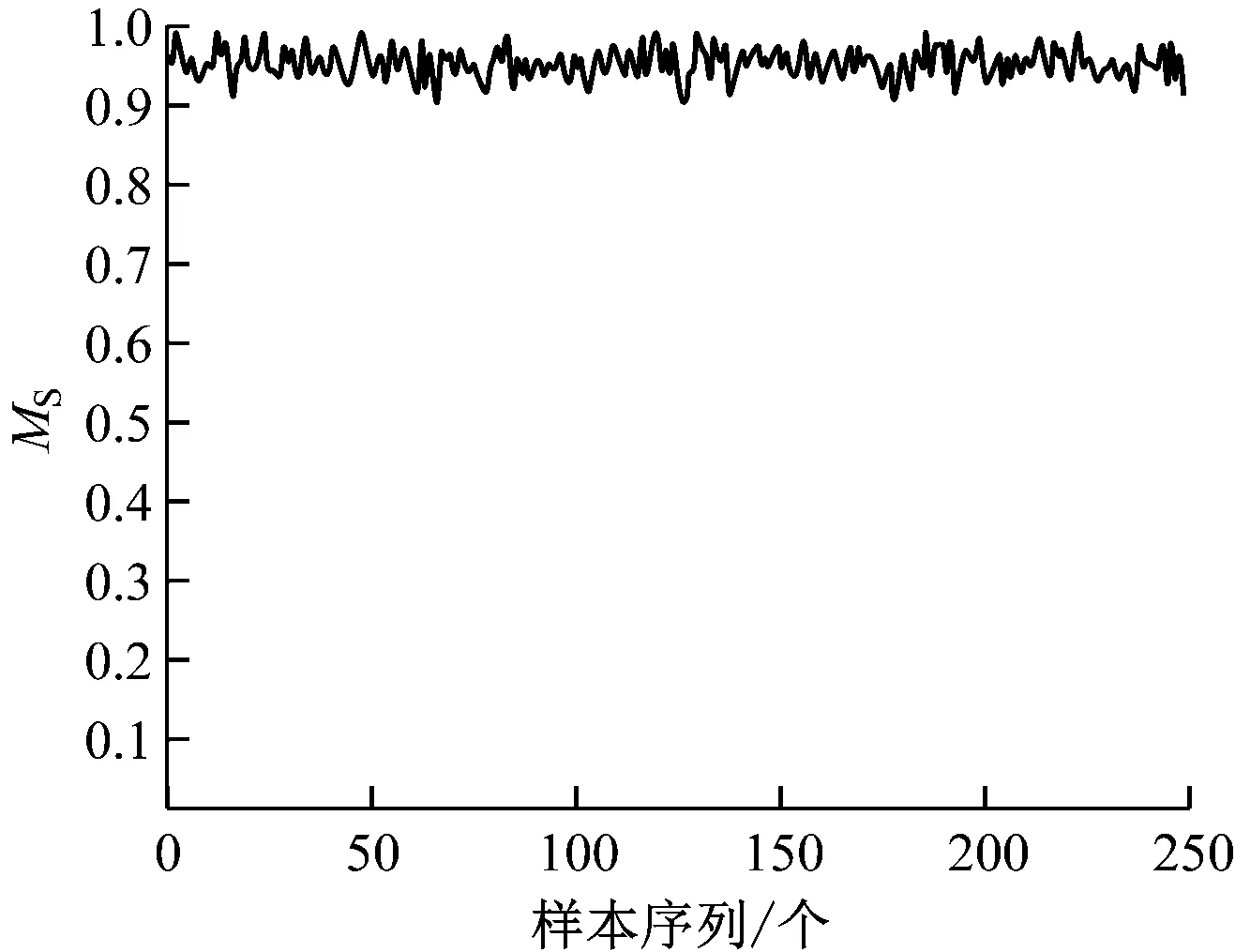
b) 預(yù)測(cè)值分布與真實(shí)值分布的MS

3 結(jié)語(yǔ)

本文通過(guò)對(duì)成都某地鐵線列車(chē)停車(chē)精度的歷史數(shù)據(jù)進(jìn)行數(shù)據(jù)分割和數(shù)據(jù)預(yù)處理，對(duì)獲得的256個(gè)樣本序列采用Weibull分布的方式對(duì)樣本數(shù)據(jù)進(jìn)行擬合，獲得了Weibull最大極值分布的尺度參數(shù)和形狀參數(shù)，以及Weibull最小極值分布的尺度參數(shù)和形狀參數(shù)。采用對(duì)時(shí)間序列預(yù)測(cè)表現(xiàn)良好的LSTM算法對(duì)這4個(gè)參數(shù)值的時(shí)間序列進(jìn)行訓(xùn)練，在100輪訓(xùn)練后用測(cè)試集對(duì)參數(shù)值進(jìn)行驗(yàn)證，其均方誤差ERMS滿(mǎn)足統(tǒng)計(jì)學(xué)的要求。因此，本文研究得到的LSTM預(yù)測(cè)模型對(duì)列車(chē)停車(chē)精度的預(yù)測(cè)有效且準(zhǔn)確。