動壓軸承的莫頓效應建模和參數(shù)分析

仝曉萌，蔡茂林，石巖，許未晴，胡永

(1.北京航空航天大學 自動化科學與電氣工程學院，北京 100191；2.沈陽鼓風機集團股份有限公司，沈陽 110869)

1 概述

動壓油膜軸承因轉(zhuǎn)速高、承載能力強等優(yōu)點被廣泛應用于航空航天、船舶重工、醫(yī)藥衛(wèi)生、食品加工等領(lǐng)域。轉(zhuǎn)子高速旋轉(zhuǎn)時，油膜中產(chǎn)生的動壓力將轉(zhuǎn)子懸浮于軸承中，使得轉(zhuǎn)子和軸承脫離接觸，而潤滑油的黏度剪切會導致油膜的溫度升高，并間接對軸承和轉(zhuǎn)子有加熱效應，通常油膜越薄，加熱效應越明顯。在同步振動下，轉(zhuǎn)子周向某處在旋轉(zhuǎn)一周過程中的平均油膜厚度低于另外一側(cè)，導致油膜對轉(zhuǎn)子加熱效應不均勻，使得轉(zhuǎn)子周向產(chǎn)生溫差。該溫差和轉(zhuǎn)子自身的熱傳導同時發(fā)生，并不相悖，且轉(zhuǎn)子的熱傳導時間常數(shù)遠大于轉(zhuǎn)子的旋轉(zhuǎn)周期，因此同步振動時轉(zhuǎn)子的周向溫度梯度無法因轉(zhuǎn)子的熱傳導而消失。非均勻加熱效應會造成轉(zhuǎn)子出現(xiàn)周向溫差和轉(zhuǎn)子的熱彎曲，進一步加劇了轉(zhuǎn)子的振動，這種現(xiàn)象被稱為莫頓效應，如圖1所示。莫頓效應是一種由多物理場耦合引起的非線性轉(zhuǎn)子失穩(wěn)現(xiàn)象，傳統(tǒng)的轉(zhuǎn)子動力學理論無法準確預測其是否存在，文獻[1]將其定義為一種未被充分理解的失穩(wěn)現(xiàn)象。莫頓效應普遍存在于油膜軸承支承的懸臂轉(zhuǎn)子系統(tǒng)中。隨著設備轉(zhuǎn)速和結(jié)構(gòu)復雜度的提高，莫頓效應已日趨普遍，其引起的過量振動具有在時域上幅值不斷增加，相位不斷變化的特點，傳統(tǒng)的機械平衡手段無法發(fā)揮作用，極易造成轉(zhuǎn)子和軸承的意外損壞[2]。建立精準的軸承和轉(zhuǎn)子模型，實現(xiàn)對莫頓效應的準確預測，對抑制或避免莫頓效應并提高設備的安全可靠性意義重大。

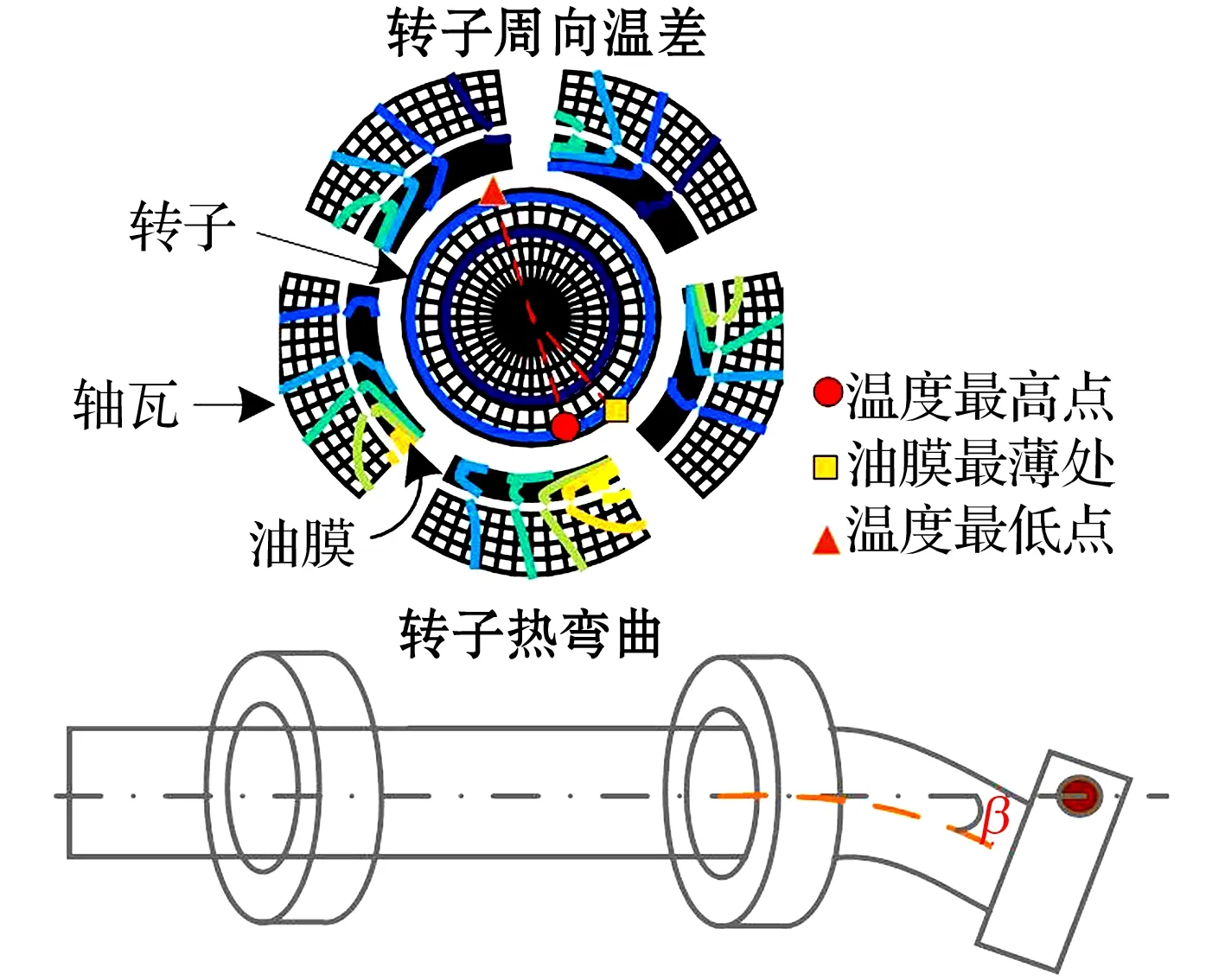
圖1 莫頓效應示意圖

當前國際上對莫頓效應的預測方法包括線性反饋法和非線性時域預測法。文獻[3]首次提出了線性反饋法，建立了軸的熱彎曲和初始彎曲間的傳遞函數(shù)，若開環(huán)傳遞函數(shù)的實部大于1，則認為轉(zhuǎn)子的熱彎曲不斷增大，最終導致系統(tǒng)不穩(wěn)定。文獻[4-5]假設轉(zhuǎn)子的振幅、周向溫差和熱彎曲導致的不平衡量均存在線性關(guān)系，若線性系數(shù)乘積的實部小于1，則認為系統(tǒng)穩(wěn)定。線性反饋法采用短軸承理論或簡化的能量方程求解油膜溫度，無法對油膜、軸承、轉(zhuǎn)子、環(huán)境間的不同熱邊界條件進行精確建模，也無法準確預測軸承和轉(zhuǎn)子的溫度場和熱變形，容易導致莫頓效應的漏報和錯報；同時，線性反饋法假設莫頓效應僅和旋轉(zhuǎn)設備的穩(wěn)定轉(zhuǎn)速相關(guān)，無法預測軸承-轉(zhuǎn)子溫度場、形變場及其導致的莫頓效應隨時間的變化，如文獻[5]在研究一臺離心式壓縮機的莫頓效應時發(fā)現(xiàn)，在穩(wěn)定轉(zhuǎn)速為11.2×103r/min時設備出現(xiàn)振動失穩(wěn)，但若將轉(zhuǎn)速從10.5×103r/min迅速升高至13.6×103r/min，設備又恢復至穩(wěn)定狀態(tài)，未出現(xiàn)莫頓效應引起的振幅過大現(xiàn)象。文獻[6-9]建立了非線性時域預測法，通過三維有限元模型求解流體(油膜、氣體)軸承的熱彈流模型，并通過建立精準的溫度場和熱變形的邊界條件，求解莫頓效應引起的轉(zhuǎn)子的周向溫差、熱彎曲和振動隨時間的變化。文獻[10]通過試驗測量了可傾瓦軸承的莫頓效應，并將轉(zhuǎn)子周向溫差與預測算法比較，驗證了預測的準確性。

莫頓效應對設備的運行參數(shù)非常敏感，工業(yè)界常通過改變軸承或轉(zhuǎn)子的結(jié)構(gòu)以達到抑制莫頓效應的目的：文獻[5]通過更換聯(lián)軸器減輕了約5 kg質(zhì)量；文獻[11]通過更換軸承將其長徑比從0.39縮減至0.33；文獻[12]將軸承間隙增加了33%，并將軸承長徑比從0.476降至0.250；文獻[13]通過研究不同轉(zhuǎn)子懸臂質(zhì)量對莫頓效應的影響，發(fā)現(xiàn)將懸臂質(zhì)量降低40%可將莫頓效應的失穩(wěn)轉(zhuǎn)速從8.0×103r/min提升至13.6×103r/min。然而，受制于安裝空間、成本、時間等因素，復雜的機械結(jié)構(gòu)變動在很多場合下無法實施。

考慮到莫頓效應本質(zhì)上是轉(zhuǎn)子在軸承內(nèi)受熱不均導致的振動失穩(wěn)現(xiàn)象，通過調(diào)整軸承的支點位置、間隙和供油溫度等來抑制莫頓效應，可避免對轉(zhuǎn)子或軸承的機械結(jié)構(gòu)大幅調(diào)整，具有更大的工程參考價值。文中首先對莫頓效應進行精準建模，然后借助實際案例驗證模型的有效性，最后對軸承支點位置、間隙和供油溫度進行參數(shù)分析，探究不同參數(shù)對莫頓效應的影響機理。

2 莫頓效應建模

2.1 油膜壓力場

通過有限元算法求解雷諾方程可以得到油膜的壓力分布P，考慮到油膜黏度μ隨溫度變化，需聯(lián)合能量方程求解溫度場分布。油膜壓力場的邊界條件如圖2所示，模型中軸承兩端的壓力設置為0，存在部分潤滑油從兩端泄漏。

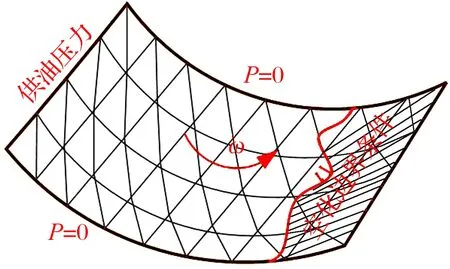
圖2 油膜壓力場邊界條件

本模型采用簡化的油液混合模型，因此供給流量和泄漏流量并不完全相等。雷諾方程為

?·(D1?P)+?D2·V+?h/?t=0，

(1)

V=[ωR,0]，

式中：h為油膜厚度；V為轉(zhuǎn)子表面線速度；ω,R分別為轉(zhuǎn)子的轉(zhuǎn)速和半徑。

2.2 油膜溫度場

通過有限元算法求解能量方程可以得到油膜的三維溫度場T，即

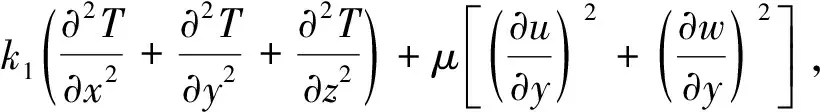
(2)

式中：ρ1,c1,k1分別為潤滑油的密度、比熱容和熱傳導率；u,w分別為油膜沿轉(zhuǎn)子周向和軸向的速度場分布。

然后更新油膜黏度為

μ=μrefexp[α(Tref-T)]，

(3)

式中：μref，Tref分別為油膜的參考黏度和溫度；α為黏溫系數(shù)。

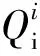
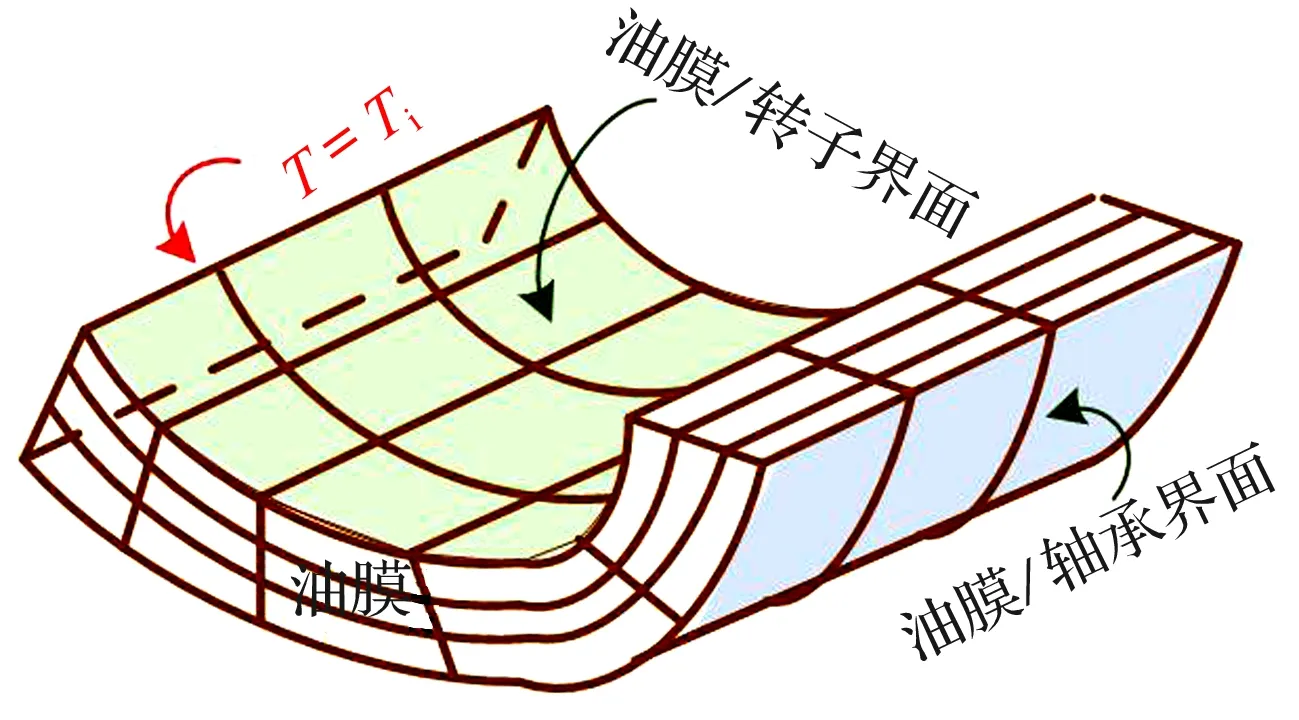
圖3 油膜溫度場的邊界條件

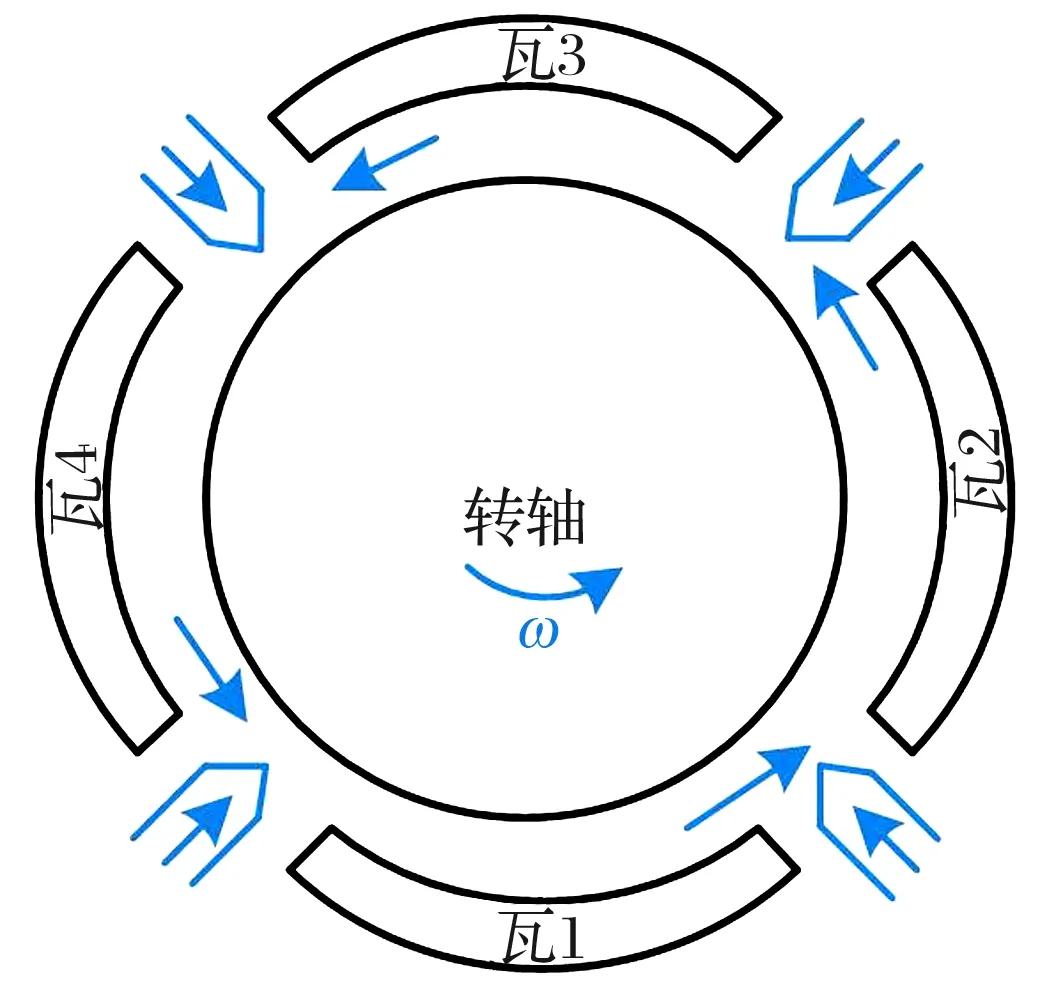
圖4 油液混合示意圖

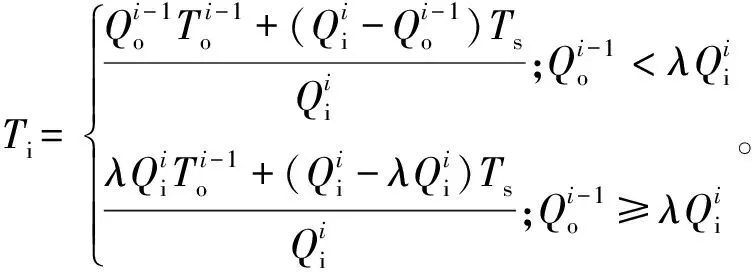
(4)

2.3 軸承和轉(zhuǎn)子溫度場

軸承和轉(zhuǎn)子暴露于空氣中的表面設置為熱對流邊界條件。通過有限元算法求解三維熱傳導方程可以得到軸承和轉(zhuǎn)子的瞬態(tài)溫度場T，即

(5)

式中：ρ,c,k分別為軸承或轉(zhuǎn)子的密度、比熱容和熱傳導率。

2.4 軸承和轉(zhuǎn)子熱變形

將軸承和轉(zhuǎn)子的溫度場作為輸入，通過有限元算法可以求解軸承和轉(zhuǎn)子的三維熱變形。若將轉(zhuǎn)軸全部劃分為三維(3D)體單元，運算量過大，不適用于轉(zhuǎn)子的瞬態(tài)分析。考慮到遠離軸承的轉(zhuǎn)子段溫升和形變不明顯，因此僅在靠近軸承的轉(zhuǎn)子段使用3D體單元，遠離軸承的轉(zhuǎn)子段使用二維(2D)梁單元以提高運算效率，并增加若干虛擬梁單元用于連接轉(zhuǎn)子3D溫度段和2D梁單元段以傳遞彎矩，轉(zhuǎn)子熱變形模型如圖5所示。通過該步驟得到的軸承和轉(zhuǎn)子熱變形會影響軸承油膜的厚度，且莫頓效應造成的轉(zhuǎn)子熱彎曲會影響轉(zhuǎn)子的動力學狀態(tài)。

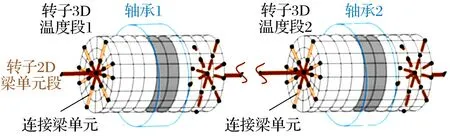
圖5 轉(zhuǎn)子熱變形模型

2.5 油膜軸承動力學模型

軸承的動力學模型如圖6所示，軸瓦在油膜壓力的作用下可繞支點轉(zhuǎn)動δ和平動yG，忽略軸瓦在壓力作用下的彈性形變，但允許軸瓦在溫升下的熱膨脹。

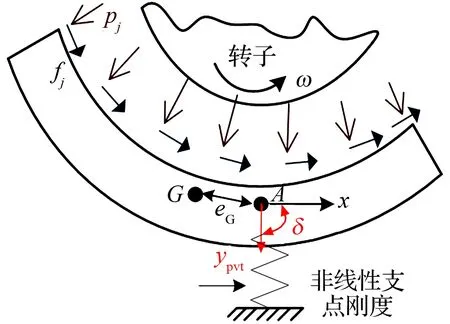
圖6 軸承動力學模型

軸承的運動方程為

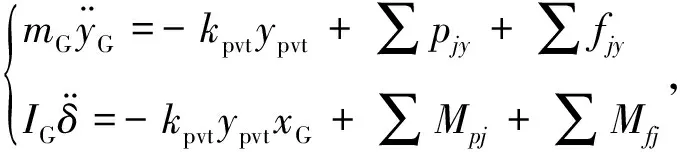
(6)

式中：mG,IG分別為軸瓦的質(zhì)量和轉(zhuǎn)動慣量；kpvt為支點剛度；ypvt為支點變形；xG,yG分別為質(zhì)心G在x，y方向上的平動位移；pjy,fjy分別為油膜在軸瓦表面網(wǎng)格節(jié)點j處沿y方向的壓力、摩擦力；Mpj,Mfj分別為pjy,fjy產(chǎn)生的壓力矩、摩擦力矩；eG為支點A到質(zhì)心G的距離。

轉(zhuǎn)子的動力學方程為

[F]=[Fm+Fg+Fb+Fe]，

(7)

式中：Mr,Cr,Kr分別為轉(zhuǎn)子的質(zhì)量、阻尼和剛度矩陣；U為有限元節(jié)點處的位移；Ubow為莫頓效應造成的熱彎曲；Fm,Fg,Fb,Fe分別為機械不平衡力、陀螺力、軸承力和其他外力。

2.6 莫頓效應預測算法

莫頓效應的預測算法如圖7所示。在程序運行的起點需設置轉(zhuǎn)子、軸承和油膜的初始溫度，轉(zhuǎn)子和軸承的初始位置；然后利用有限元方法求解軸承和轉(zhuǎn)子的瞬態(tài)位置，即通過雷諾方程求解油膜壓力場和速度場，通過能量方程求解油膜溫度場和黏度，考慮到油液的黏度和溫度是相互耦合的，因此需在時域上交替求解雷諾方程和能量方程并及時更新油膜溫度場和黏度；若軸承和轉(zhuǎn)子的運動狀態(tài)收斂，則程序繼續(xù)求解軸承和轉(zhuǎn)子的三維溫度場分布，否則程序返回至動力學求解器；隨后程序根據(jù)軸承和轉(zhuǎn)子的三維溫度場分布計算軸承和轉(zhuǎn)子的熱變形，并更新油膜的厚度和轉(zhuǎn)子軸向的熱彎曲，作為下個循環(huán)的動力學求解器的輸入。

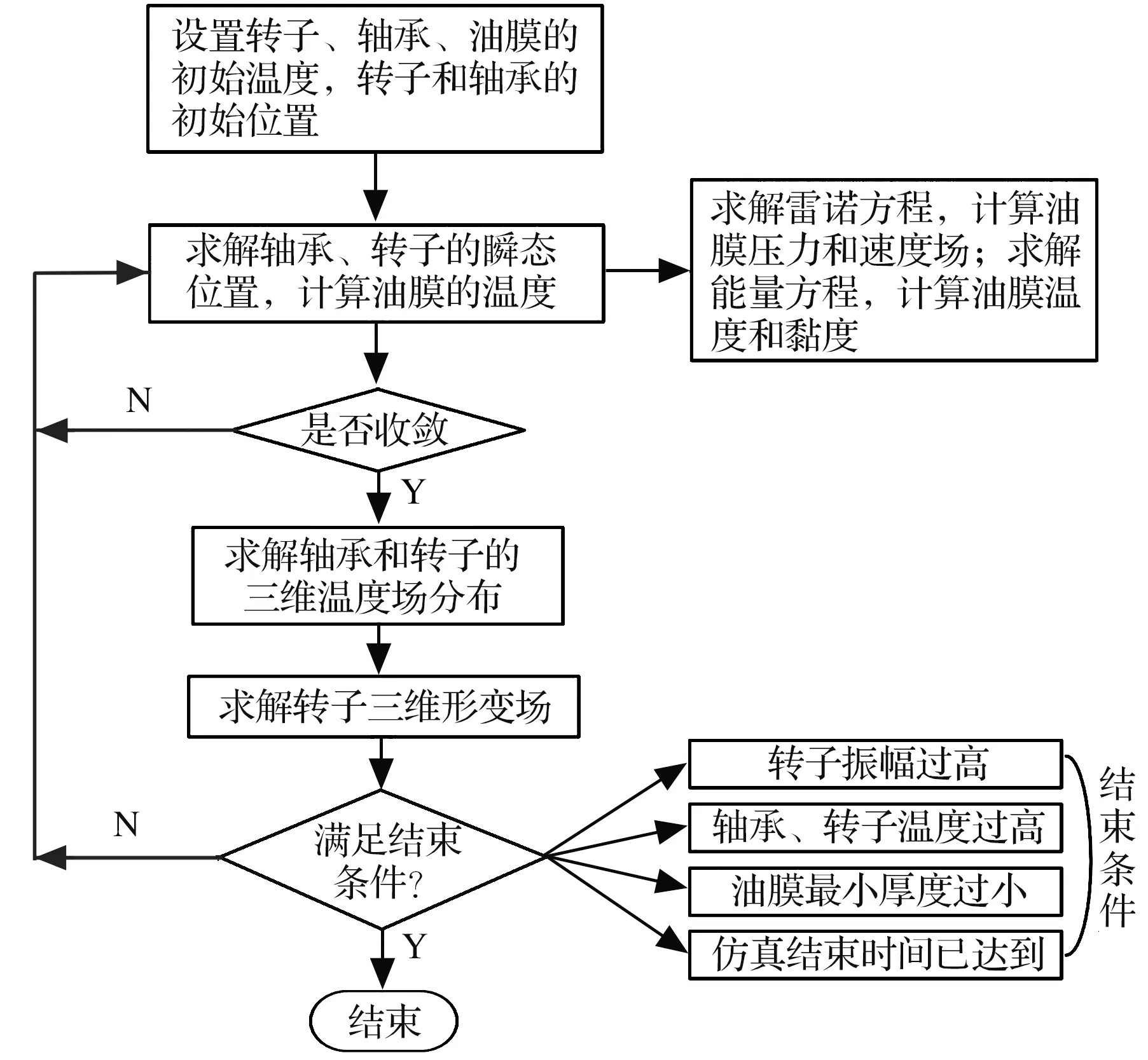
圖7 莫頓效應預測算法

3 實例驗證

文獻[5]在測試圖8所示的壓縮機時發(fā)現(xiàn)，當轉(zhuǎn)速接近8 000 r/min時，莫頓效應造成轉(zhuǎn)子振動失穩(wěn)，在數(shù)分鐘內(nèi)，轉(zhuǎn)子的振動幅度過大導致系統(tǒng)自動停機保護，該轉(zhuǎn)子通過雙軸承支承，懸臂端的可傾瓦軸承造成了莫頓效應。以圖8所示壓縮機轉(zhuǎn)子-軸承模型為例，驗證本文建立的莫頓效應模型的有效性，為簡化轉(zhuǎn)子動力學模型，遠離懸臂端的軸承的剛度和阻尼被固定為常數(shù)，其溫度效應被忽略，系統(tǒng)的主要參數(shù)見表1。

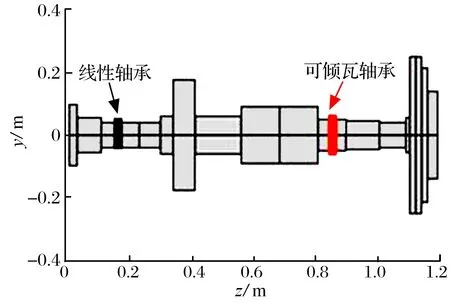
圖8 壓縮機轉(zhuǎn)子-軸承模型

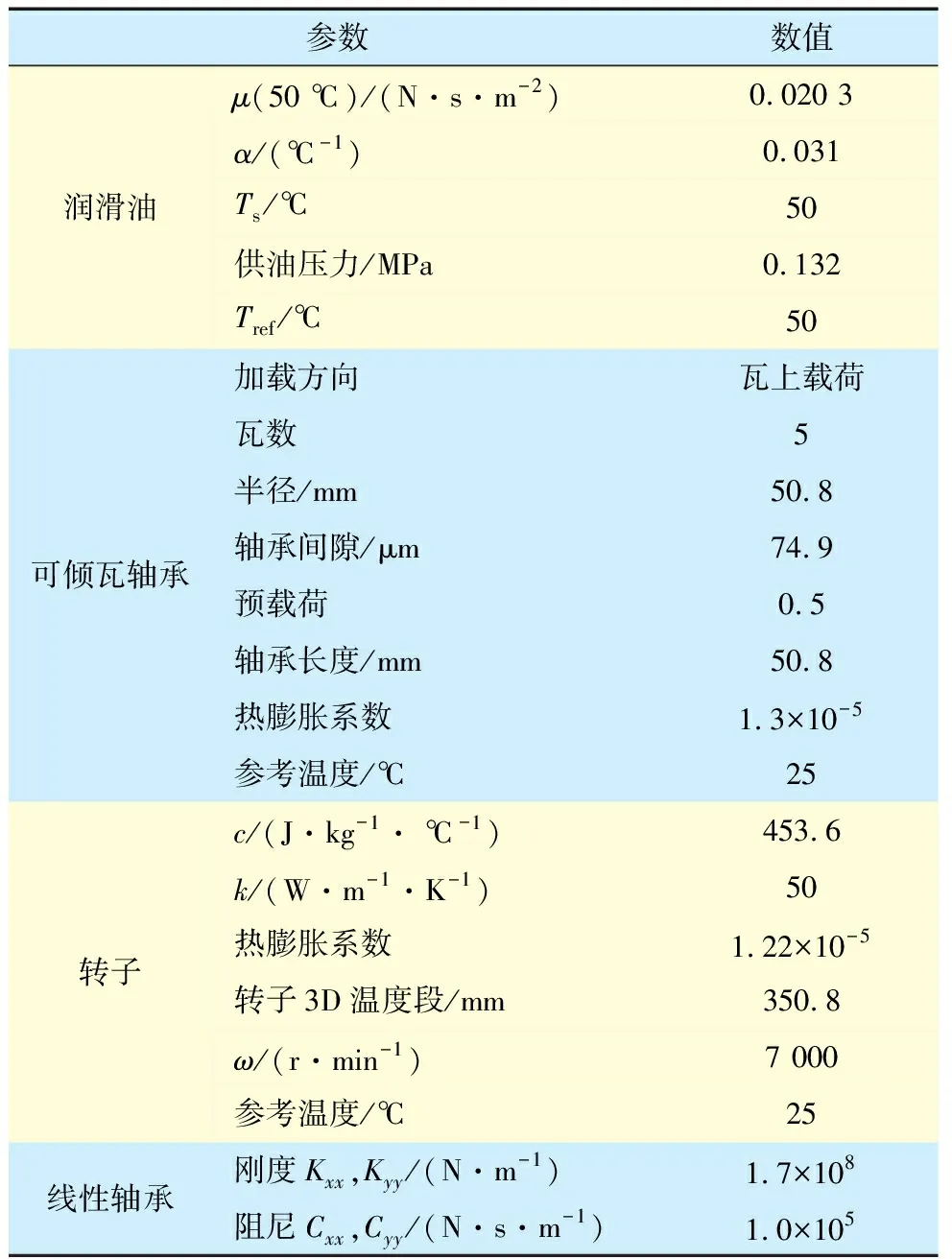
表1 壓縮機轉(zhuǎn)子-軸承模型的主要參數(shù)

軸瓦、油膜和轉(zhuǎn)子在第139 s的等溫線如圖9所示，可以清晰看到轉(zhuǎn)子的周向存在溫度梯度，高溫點和低溫點相距約180°相位。轉(zhuǎn)子在軸承處的振動如圖10所示，可以看到轉(zhuǎn)子的振幅和相位隨時間不斷變化呈螺旋狀，因此莫頓效應無法通過傳統(tǒng)手段進行機械配平。由圖9和圖10可知，此時系統(tǒng)振幅過大，表明7 000 r/min已接近系統(tǒng)的失穩(wěn)轉(zhuǎn)速，這和文獻[5]觀察的現(xiàn)象接近。

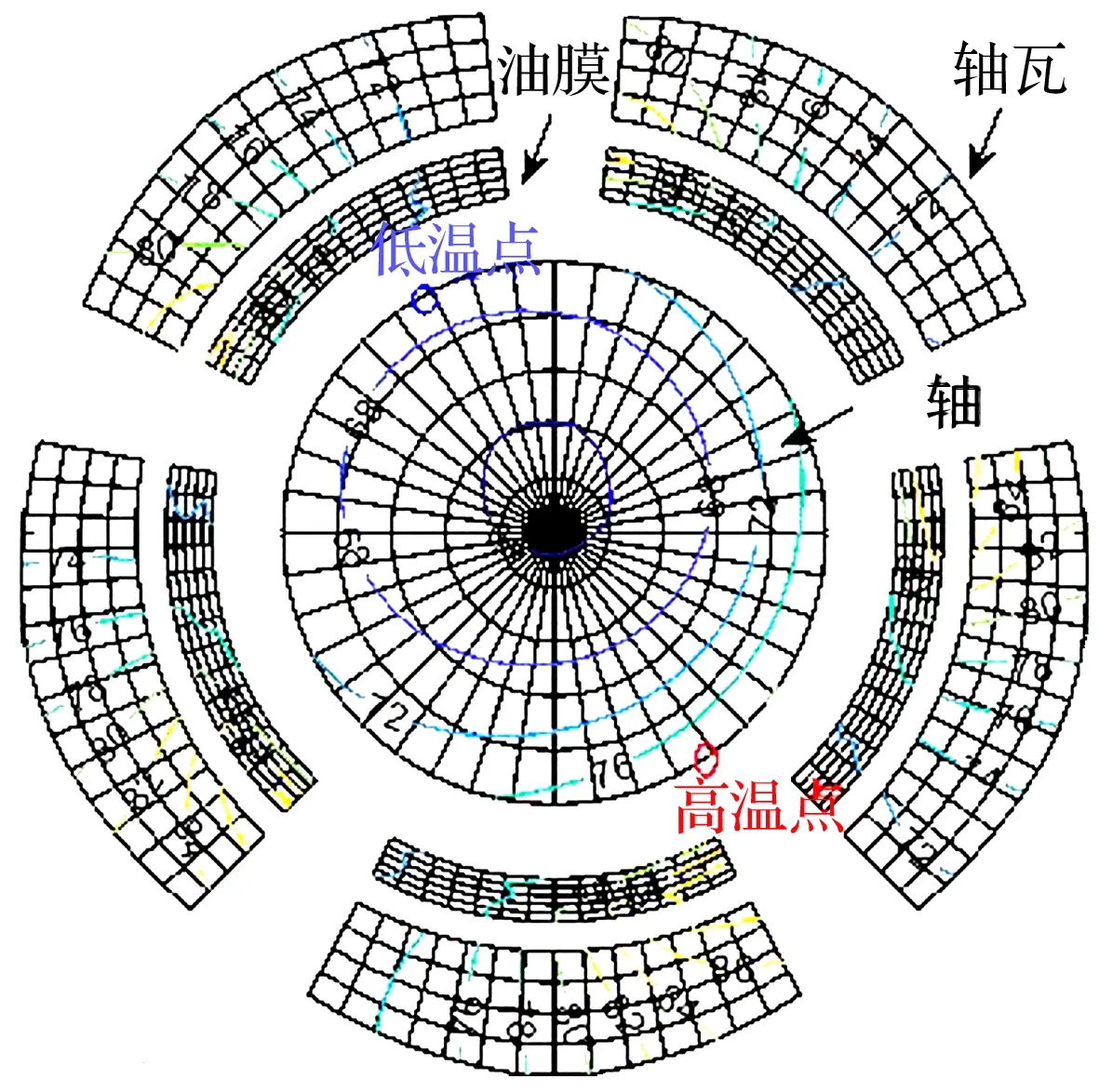
圖9 第139 s時軸承中軸截面的等溫線

圖10 供油溫度為50 ℃時轉(zhuǎn)子在軸承處的振動曲線

4 參數(shù)分析

4.1 軸承的支點偏移系數(shù)

可傾瓦軸承的支點偏移系數(shù)為0.5，即該軸瓦為對稱結(jié)構(gòu)，轉(zhuǎn)子可沿正向或逆向旋轉(zhuǎn)，如圖9所示；當支點偏移系數(shù)超過0.6時，軸承的支點向軸瓦末端偏移，轉(zhuǎn)子只允許單向旋轉(zhuǎn)，如圖6所示。為探究不同支點偏移系數(shù)對莫頓效應的影響，選取最廣泛的支點偏移系數(shù)0.5和0.6進行對比分析。2種偏移系數(shù)下轉(zhuǎn)子在軸承處的振幅如圖11所示，可以發(fā)現(xiàn)當偏移系數(shù)為0.6時，轉(zhuǎn)子的振幅降低了約80%；不同偏移系數(shù)下轉(zhuǎn)子的均溫和周向溫差如圖12所示，可以發(fā)現(xiàn)當偏移系數(shù)為0.6時，轉(zhuǎn)子的均溫和周向溫差均降低：表明將軸承的支點偏移系數(shù)從0.5增加到0.6，不僅可以有效降低轉(zhuǎn)子溫度，還可成功抑制莫頓效應。分析原因：1)在多數(shù)情況下，增加支點偏移系數(shù)可提高軸承的承載能力和剛度，導致系統(tǒng)的臨界轉(zhuǎn)速升高，考慮到莫頓效應和臨界轉(zhuǎn)速對應的模態(tài)振型(尤其是懸臂處振幅較大的振型)緊密相關(guān)，提高相應的臨界轉(zhuǎn)速，也提高了莫頓效應的失穩(wěn)轉(zhuǎn)速[8]，使該失穩(wěn)轉(zhuǎn)速遠離當前運行轉(zhuǎn)速；2)增加支點偏移系數(shù)增加了軸承承載區(qū)油膜的平均厚度，有利于減少油膜對軸承的加熱效應，因此轉(zhuǎn)子的均溫和周向溫差均下降。

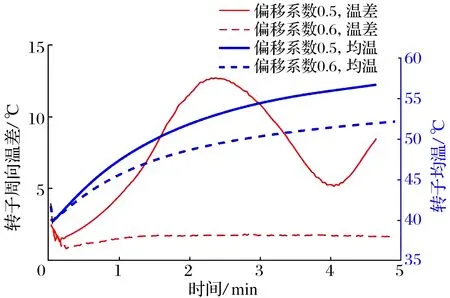
圖12 不同支點偏移系數(shù)下的轉(zhuǎn)子周向溫差和均溫

4.2 軸承間隙

為研究軸承間隙對莫頓效應的影響，現(xiàn)將表1中的軸承間隙增加20%，其余參數(shù)保持不變。考慮到莫頓效應是由轉(zhuǎn)子周向溫差導致的振動失穩(wěn)現(xiàn)象，且轉(zhuǎn)子溫差造成的熱彎曲和轉(zhuǎn)子振動在時域上相互耦合，造成轉(zhuǎn)子振動相位不斷變化，振幅隨時間波動，相應的油膜厚度也隨時間改變。不同軸承間隙下轉(zhuǎn)子在軸承處的振幅和最小油膜厚度如圖13所示，增加軸承間隙20%可有效降低轉(zhuǎn)子振幅約85%，且最小油膜厚度從不足0.2Cb增加到0.4Cb(Cb=74.9 μm，為軸承設計間隙，見表1)。不同軸承間隙下轉(zhuǎn)子周向溫差和均溫如圖14所示，增加軸承間隙20%既可降低轉(zhuǎn)子的均溫又可以減少轉(zhuǎn)子的周向溫差。由上述結(jié)果可知，增加軸承間隙，可降低潤滑油對轉(zhuǎn)子的加熱效應，有利于抑制莫頓效應，但過度增加軸承間隙，將顯著改變軸承剛度和阻尼，并影響軸承-轉(zhuǎn)子系統(tǒng)的臨界轉(zhuǎn)速、振動等特性，需謹慎實施。

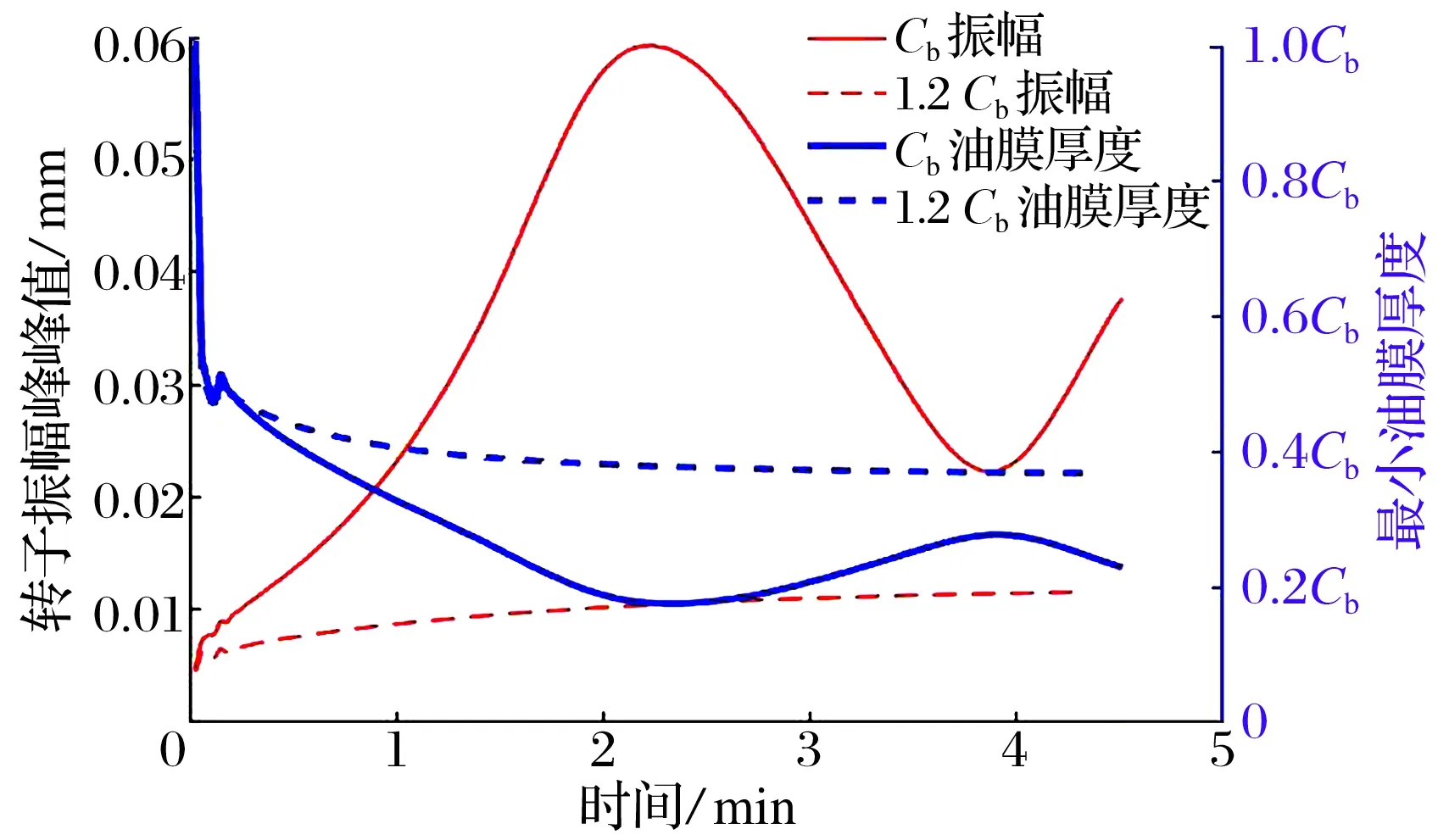
圖13 不同軸承間隙下的轉(zhuǎn)子振幅和油膜厚度

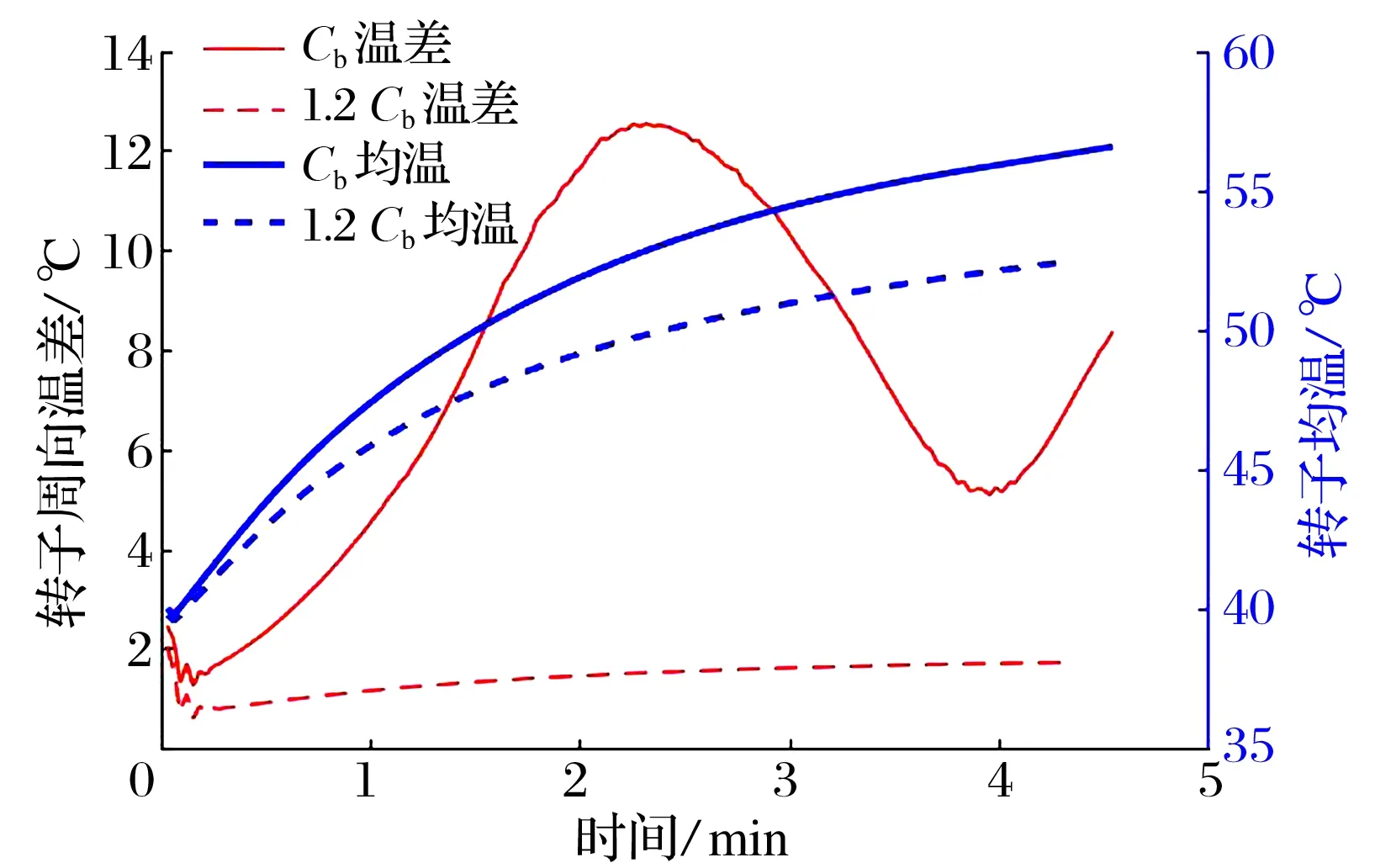
圖14 不同軸承間隙下的轉(zhuǎn)子周向溫差和均溫

4.3 供油溫度

為探究軸承的供油溫度對莫頓效應的影響，現(xiàn)將表1中的供油溫度從50 ℃降低至30 ℃，轉(zhuǎn)子在軸承處的振動曲線如圖15所示，莫頓效應造成轉(zhuǎn)子的振動呈螺旋式增長，表現(xiàn)為振幅不斷增加，相位持續(xù)變化；對比圖10可知，轉(zhuǎn)子的最大振幅隨供油溫度降低而增大。不同供油溫度下的轉(zhuǎn)子周向溫差和均溫如圖16所示，不難發(fā)現(xiàn)，降低供油溫度時，轉(zhuǎn)子的平均溫度降低，周向溫差反而增大。不同供油溫度下的最小油膜厚度和平均油膜厚度如圖17所示，將供油溫度從50 ℃降至30 ℃，油膜的平均厚度增加了約0.1Cb，而最小油膜厚度未出現(xiàn)明顯變化。圖17中平均油膜厚度在仿真初始階段迅速降低，這是由于轉(zhuǎn)子和軸承的初始溫度被設置在40 ℃，高于常溫時，轉(zhuǎn)子和軸承的熱膨脹將減小軸承的實際工作間隙。

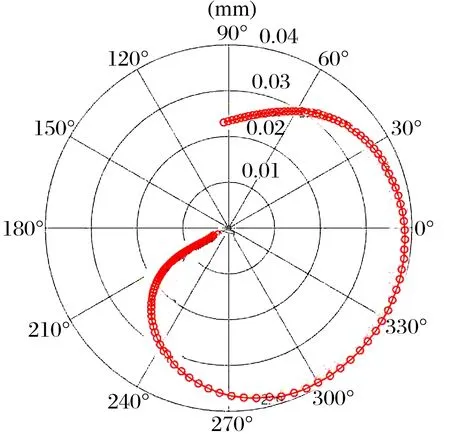
圖15 供油溫度30 ℃時轉(zhuǎn)子在軸承處的振動曲線

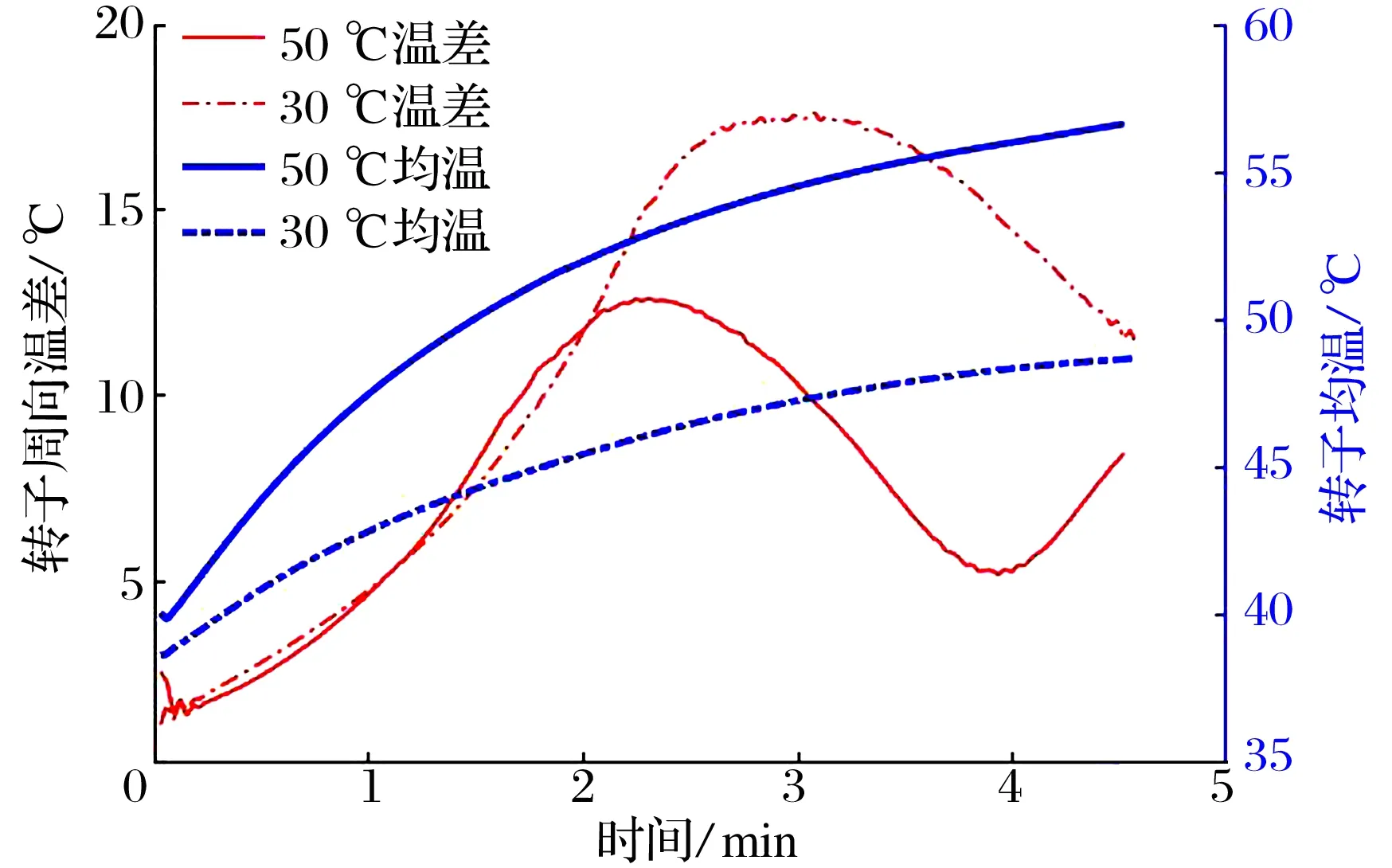
圖16 不同供油溫度下的轉(zhuǎn)子溫差和均溫

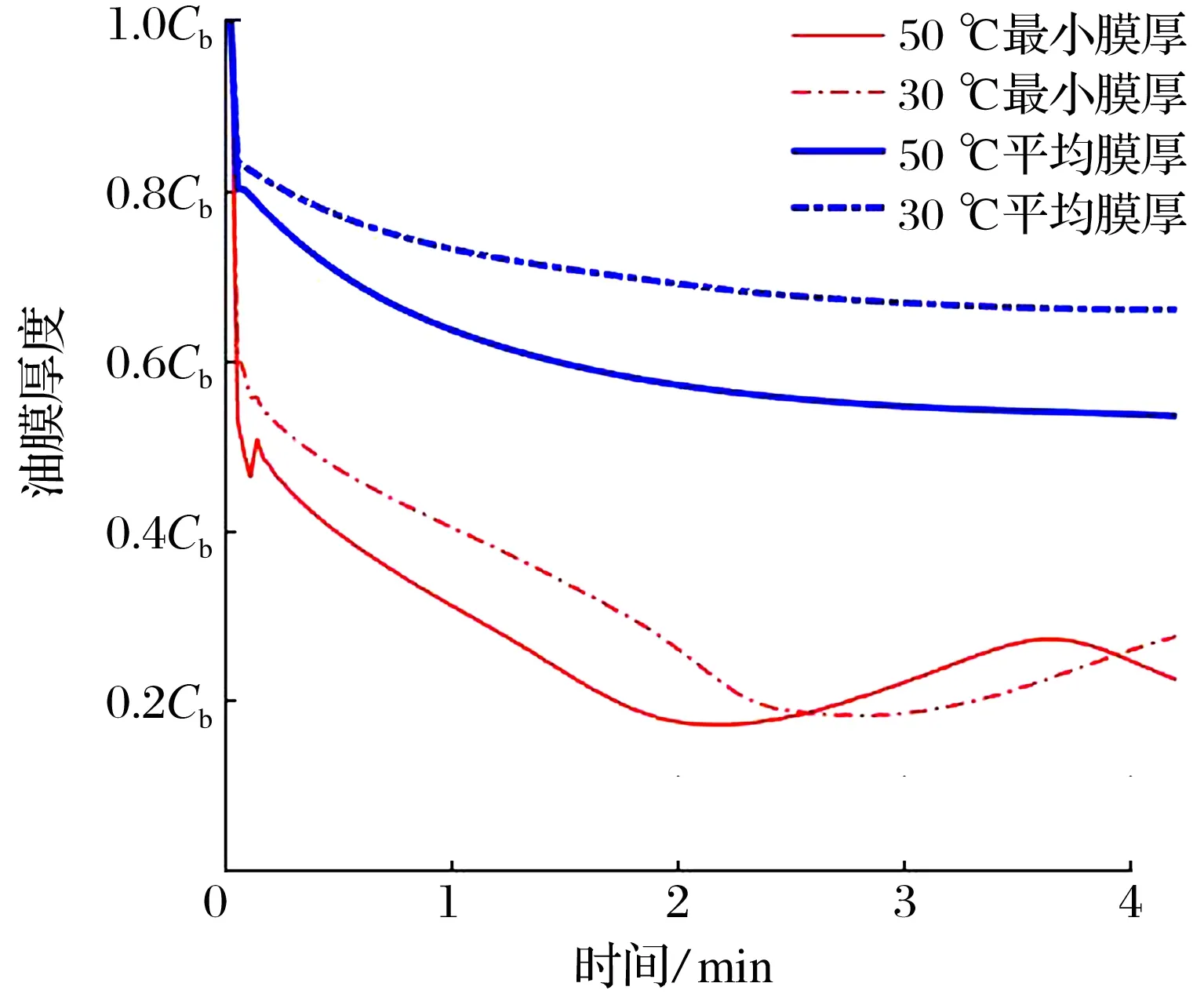
圖17 不同供油溫度下的平均和最小油膜厚度

以上結(jié)果表明，降低供油溫度可以降低軸承和轉(zhuǎn)子的運行溫度，提高軸承的實際工作間隙；但由于降低油溫會顯著增加油液黏度(在該例中約86%)，反而加劇油膜對軸承的非對稱加熱效應，導致轉(zhuǎn)子的周向溫差不降反升，轉(zhuǎn)子熱彎曲也更強烈：因此降低軸承的供油溫度在該實例中無法有效抑制莫頓效應。

5 結(jié)論

本文對可傾瓦動壓油膜軸承進行了精準的熱彈流建模，通過編寫三維有限元軟件求解轉(zhuǎn)子-軸承系統(tǒng)的動力學、溫度和熱變形，并在時域上預測莫頓效應，通過分析軸承的支點偏移系數(shù)、軸承間隙和供油溫度對莫頓效應的影響，得到如下結(jié)論：

1)建立的基于三維有限元模型的莫頓效應預測算法可準確預測轉(zhuǎn)子熱彎曲造成的振動失穩(wěn)。

2)將可傾瓦軸承的支點偏移系數(shù)從0.5增加至0.6，可有效降低轉(zhuǎn)子的平均溫度和周向溫差，進而抑制莫頓效應和振動失穩(wěn)現(xiàn)象。

3)適當增加軸承間隙，可降低油膜對軸承的加熱效應，有利于抑制莫頓效應，考慮到該間隙和軸承的剛度阻尼特性息息相關(guān)，需謹慎調(diào)整軸承間隙，以防止對系統(tǒng)的臨界轉(zhuǎn)速和振動特性產(chǎn)生不利影響。

4)降低軸承的供油溫度，導致潤滑油的黏度升高，加劇了油膜對轉(zhuǎn)子的非對稱性加熱效應，使得轉(zhuǎn)子的周向溫差升高，加劇了莫頓效應。