安裝誤差對弧線齒面齒輪接觸特性影響分析

趙玉龍，馮占榮，郭正華，熊光勁，高凌鋒

（南昌航空大學 航空制造工程學院，南昌 330063）

0 引言

面齒輪[1～3]傳動是一種新型的齒輪傳動，具有重合度大、傳動平穩、振動小等優點[4]，主要應用于直升機主減速器的動力分流機構，適應于高速、重載的工作環境。面齒輪的嚙合分析在面齒輪設計與制造中有著重要的影響，其中接觸應力與接觸區域是影響齒輪副傳動的承載能力、傳動效率以及噪聲等綜合技術指標，因此要著重研究該方面。目前，國外在面齒輪傳動接觸應力方面研究，主要為F.L.Litvin等[5～7]利用TCA（tooth contact analysis）理論，結合有限元方法對面齒輪嚙合點處接觸應力和嚙合位置做了大量研究，得到了不同嚙合位置對其的影響規律。國內，趙寧[8,9]分別對直齒與斜齒面齒輪齒面仿真以及接觸應力進行了研究；陳書涵[10]對含安裝誤差對直齒面齒輪傳動接觸軌跡與接觸應力進行了研究，得出了直齒面齒輪安裝誤差與接觸軌跡與應力的變化規律；在弧線齒面齒輪方面，沈云波[11]對弧線齒面齒輪傳動承載接觸進行了分析,利用有限元的方法得到面齒輪在一定外加扭矩的情況下齒面載荷分布均勻。蘇進展[12]對弧線齒面齒輪齒面接觸進行了分析，分析了產形齒輪齒數、刀傾角和刀尖半徑對齒面接觸印痕的影響。以上關于直齒面齒輪的齒面設計及齒面接觸研究成果較為詳實，對于弧線齒面齒輪相關研究還較少。

本文主要對弧線齒面齒輪的幾何展成方法以及輪齒接觸進行了分析，提出包含安裝誤差的弧線齒面齒輪展成方法以及嚙合點主曲率與最大接觸應力的算法，研究了安裝誤差對接觸軌跡與最大接觸應力的影響規律。

1 弧線齒面齒輪副的齒面方程推導

1.1 弧線齒圓柱齒輪齒面方程的推導

采用刀具漸開線弧線齒圓柱齒輪展成的方法來加工弧線齒面齒輪，利用假想刀具齒輪與被加工圓柱齒輪的嚙合運動，展成加工出被加工圓柱齒輪。建立圖1刀具漸開線弧線齒圓柱齒輪齒輪坐標系Os和Oh，其中圖2與圖3分別為弧線齒圓柱齒輪齒線截面圖與圓柱齒輪截面圖。

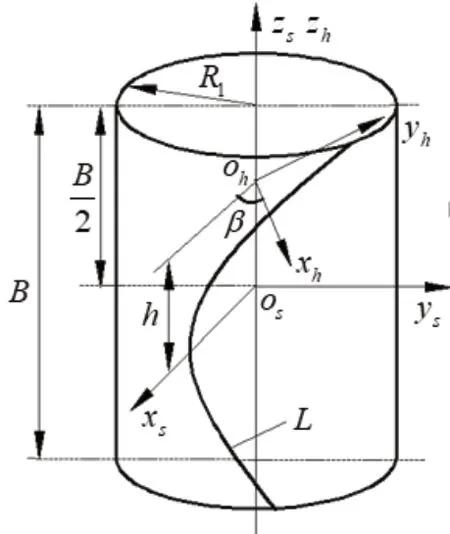
圖1 弧線齒圓柱齒輪坐標系

圖2 圓柱齒輪齒線截面圖

圖3 圓柱齒輪截面圖

可以得到在坐標系Os下漸開線圓柱齒輪齒面方程為：

坐標系Oh到Os坐標變換矩陣為：

經坐標變換可得到刀具漸開線弧線齒圓柱齒輪齒面方程為：

式(5)中B為漸開線弧線齒圓柱齒輪齒寬，R1分度圓半徑，Rb為基圓半徑，其中L在分度圓柱面上的展開圖上的標準圓弧，圓弧半徑為RT，θS是漸開線上一點的角度參數，θS0是漸開線起始點的角度參數，方程中±號代表兩側齒面，β為位置角，h為齒寬參數。

1.2 弧線齒面齒輪齒面方程的推導

圖4所示為刀具齒輪展成加工出弧線齒面齒輪的坐標系，O0、O2分別為刀具齒輪和弧線齒面齒輪固定坐標系，O1、O3分別為刀具齒輪和弧線齒面齒輪的旋轉坐標系。刀具展成加工弧線齒面齒輪時，就像是模擬兩個齒輪的嚙合過程，其中φ1和φ3分別為刀具齒輪和面齒輪展成時所轉過的角度。

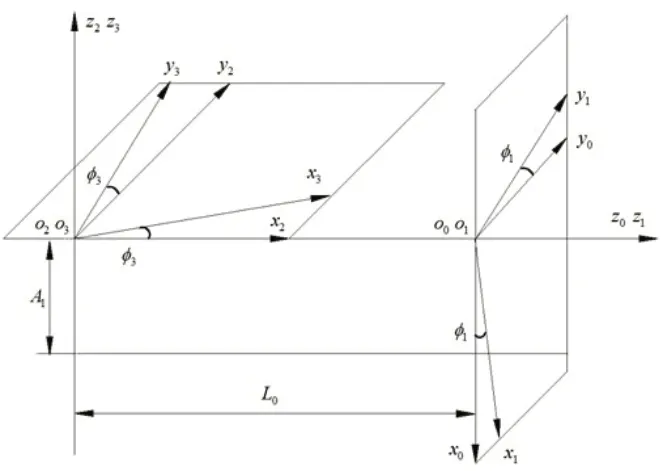
圖4 正交弧線齒面齒輪坐標系

其中得到從弧線齒圓柱齒輪動坐標系轉換到面齒輪動坐標系的變換矩陣為：

經坐標變換可得弧線齒面齒輪齒面方程為：

其中弧線齒面齒輪齒面單位法向量為：

其中，L31為坐標轉換矩陣M31的前三行和前三列元素組成的子矩陣。

由齒輪嚙合原理可知，圓柱齒輪與面齒輪嚙合條件式為：

其中v(1,3)為刀具齒輪與被加工面齒輪的齒面接觸處的相對速度。可根據嚙合條件式(9)得到φ1與θS和h的關系，將這兩個值離散化取值代入到弧線齒面齒輪齒面方程式(7)聯立求解，即可以到面齒輪工作曲面方程。

2 齒面接觸分析

弧線齒圓柱齒輪和面齒輪的傳動中，若采用與面齒輪加工刀具參數完全一致的弧線齒圓柱齒輪，則嚙合傳動形式為線接觸，這種理想傳動形式很難實現，相反還可能因邊緣接觸而發生偏載，破壞正常傳動。在這里我們采用實際參與嚙合的弧線齒圓柱齒輪比刀具齒輪齒數少1～3，形成點接觸的傳動形式，其余參數均與刀具齒輪相同，因此只需將刀具齒輪的下標“S”改為“1”即可。

∑S與∑1為分別為刀具齒面與嚙合傳動的弧線齒圓柱齒輪齒面，圖5為假想的內嚙合情形，其中rbs、rb1分別為刀具齒輪和弧線齒圓柱齒輪基圓半徑，rs、r1分別為刀具齒輪和弧線齒圓柱齒輪分度圓半徑，其中b為兩齒輪轉軸之間的最短距離由式(10)決定：

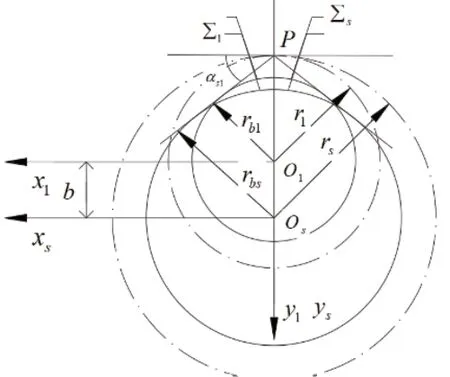
圖5 刀具齒輪與被加工齒輪假想內嚙合圖

齒輪接觸分析（TCA）就是通過計算機仿真進行嚙合與接觸的過程，建立如圖6弧線齒面齒輪接觸分析坐標系，在固定坐標系O1c下，弧線齒圓柱齒輪與面齒輪齒面∑1與∑2進行嚙合接觸，可知嚙合點的位置矢量和單位法向量相等。建立如圖7和圖8包含安裝誤差的弧線齒面齒輪嚙合傳動坐標系，將其代入弧線齒面齒輪接觸分析坐標系中。

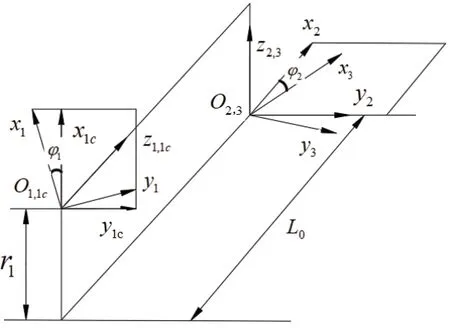
圖6 弧線齒面齒輪接觸分析坐標系

圖7 含安裝誤差的弧線齒面齒輪副嚙合坐標系

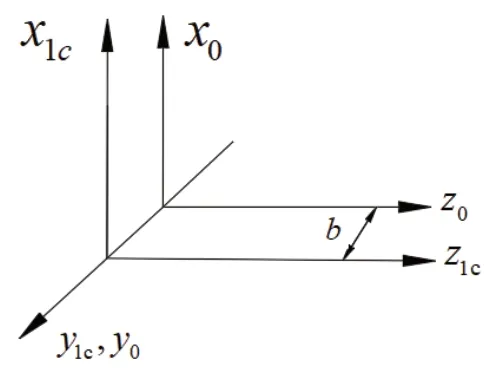
圖8 刀具與弧線齒圓柱齒輪坐標關系

其中O1c為弧線齒圓柱齒輪的固定坐標系，Oh和Oq為輔助坐標系，模擬齒輪間的裝配誤差。ΔE為軸偏置安裝誤差，Δq為軸向位移安裝誤差，Δγ為軸夾角安裝誤差。在弧線齒圓柱齒輪固定坐標系O1c下，弧線齒圓柱齒輪與面齒輪的位置矢量與法向量分別為：

式中，φ1與φ2分別為弧線齒圓柱齒輪與弧線齒面齒輪嚙合時的轉角。M1c,1為弧線齒圓柱齒輪動坐標系到靜坐標系的齊次變換矩陣，L1c,1為齊次變換矩陣M1c,1的旋轉矩陣。M1c,3為弧線齒面齒輪轉動坐標系到弧線齒圓柱齒輪固定坐標系的齊次變換矩陣，L1c,3為齊次變換矩陣M1c,3的旋轉矩陣。弧線齒面齒輪傳動嚙合接觸的基本方程為：

將上式方程(16)向x,y,z軸投影，可得6個標量方程，其中=1，得到5個獨立的方程，聯合嚙合方程(9)，即有6個方程，7個未知數，給一定步長φ1的值，可求出其他6個未知量，將求得的值代回弧線齒面齒輪方程，可以得到完整的面齒輪齒面的嚙合線。

3 弧線齒面齒輪接觸點主曲率與接觸應力計算

根據微分幾何理論，曲面的曲率可以由兩類基本量來確定，用E,F,G,L,M,N來表示。弧線齒面齒輪曲面的參數方程可以用r=r(u,v)表示，其中u、v表示齒面參數。假設曲面上的一點P(u,v)，則該曲面的單位法向矢量為：

其中E=ruru，F=rurv，G=rvrv，L=-nuru，M=-nu rv，N=rvvn。

則P(u,v)點沿方向du/dv的法曲率kn為：

化簡公式(18)則得到主曲率的計算公式為：

該方程存在兩個不同的實數解，就是弧線齒面齒輪上一點處兩個不同的主曲率，而且主方向相互垂直。其中K11與K12為弧線齒圓柱齒輪兩個主曲率；K21與K22為面齒輪兩個主曲率，將兩個齒面方程按上述步驟計算即可求得。

基于赫茲接觸理論，如圖9可知在假設弧線齒面齒輪與漸開線齒面在O點接觸，負載的轉矩T已知，弧線齒面齒輪與弧線齒圓柱齒輪嚙合方式為點接觸，在嚙合點O的法向接觸力Fn的作用線與其法線共線，可知其法向接觸力與基圓相切，得齒面接觸點法向接觸力為：

圖9 弧線齒面齒輪嚙合點法向力

式(20)中，T為弧線齒圓柱齒輪施加的轉矩，Rb1為圓柱齒輪基圓半徑。

其中接觸點處最大接觸應力σmax為：

式(21)中，a接觸橢圓長半軸、b短半軸，可以由式(22)求出：

其中，α、β、γ為計算系數，其值由cosθ=B/A確定，可查表并線性插值得到。E1、E2，μ1、μ2分別為弧線齒圓柱齒輪和弧線齒面齒輪材料的彈性模量和泊松比。其中A,B關于兩個齒面接觸主曲率的方程，可由式(23)得出：

4 算例

4.1 安裝誤差對面齒輪接觸軌跡影響

表1為弧線齒面齒輪傳動副的基本參數。圖10為弧線齒面齒輪傳動副裝配圖。根據前文提到的公式(16)編寫MATLAB文件，分別對三種安裝誤差進行軌跡接觸分析所得結果如圖11～圖13所示。其中，T為弧線齒圓柱齒輪施加的轉矩為T=24N·m；泊松比μ1=μ2=0.3，彈性模量為E1=E2=2.07×105MPa。

表1 弧線齒面齒輪副基本參數

圖10 弧線齒面齒輪副

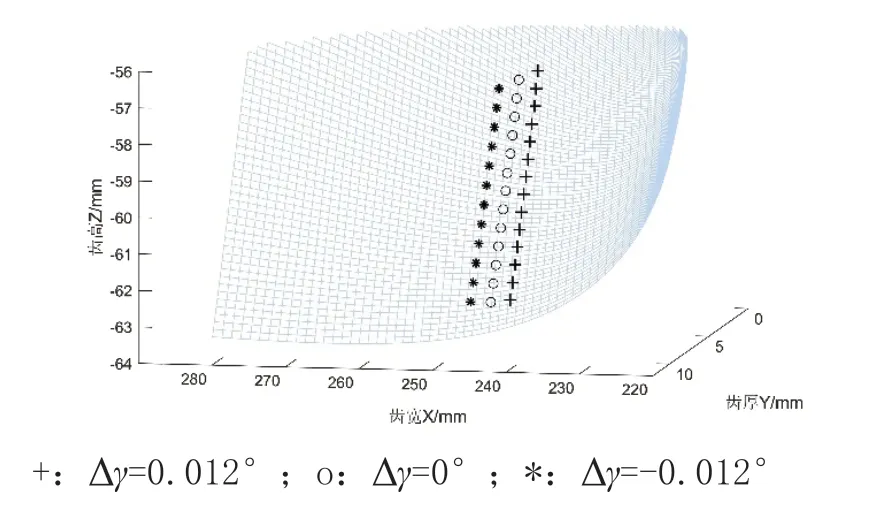
圖11 軸交角誤差對接觸軌跡的影響

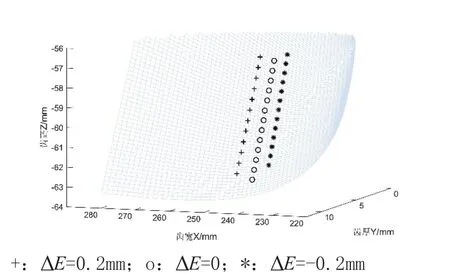
圖12 軸交錯誤差對接觸軌跡的影響

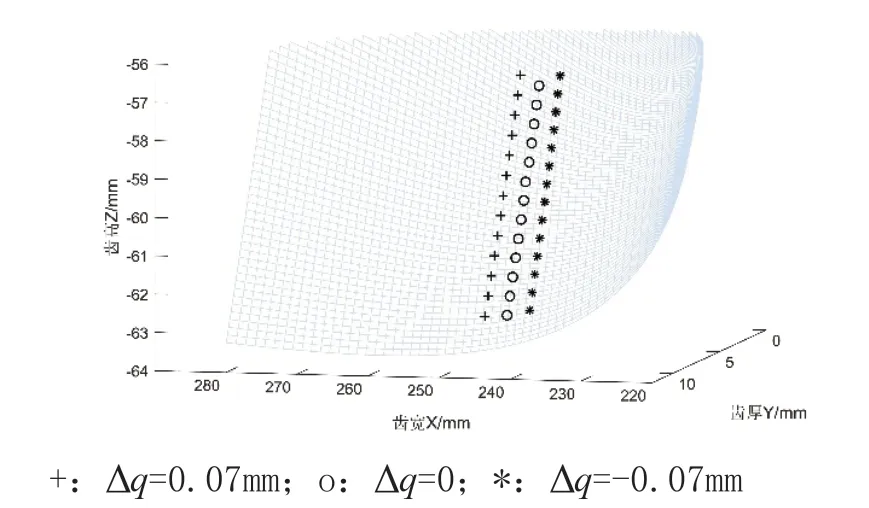
圖13 軸偏移誤差對接觸軌跡影響

對圖11～13分析可知，三幅圖的接觸軌跡類似在一條從齒頂到齒根的直線上，軸交角誤差為正，可知嚙合點軌跡是向面齒輪內端移動，軸交角誤差為負，嚙合點軌跡向面齒輪外端移動。軸交錯誤差為正，嚙合點軌跡向面齒輪外端移動，軸交錯誤差為負時，嚙合點軌跡向面齒輪齒面內端移動。軸偏移誤差為正時，嚙合點軌跡向面齒輪齒面外端移動，當軸偏移誤差取負時，嚙合點軌跡向面齒輪內端移動。

相比較三種誤差對嚙合點軌跡的影響，軸交錯誤差取值偏大，接觸軌跡移動與其他兩種誤差偏移相近，可以得出軸交錯誤差對接觸軌跡影響相對較小。但軸交角誤差取值很小，接觸軌跡已發生較大移動，所以在安裝面齒輪副時，要嚴格控制軸交角誤差。

4.2 裝配誤差對單齒最大接觸應力影響

根據表1中面齒輪副的基本設計參數，結合式(20)～式(23)對面齒輪嚙合點的長短半軸以及單齒最大接觸應力進行相關計算，所得仿真結果如圖14～圖16所示。

分析圖14～圖16我們可以得出結論：

通過計算，當弧線齒面齒輪齒面上的嚙合點從齒頂位置向齒根位置移動時，嚙合點的橢圓長軸在減小，短軸在增大，因而從圖14～圖16可以看出最大接觸應力是先減小，后減小緩慢；在有安裝誤差的情況下，最大接觸應力先減小后有增大的趨勢。

由圖14可知，當軸交角誤差為正時，嚙合點的最大接觸應力大于無誤差的最大接觸應力，當軸交角誤差為負時，嚙合點的最大接觸應力小于正常的最大接觸應力。

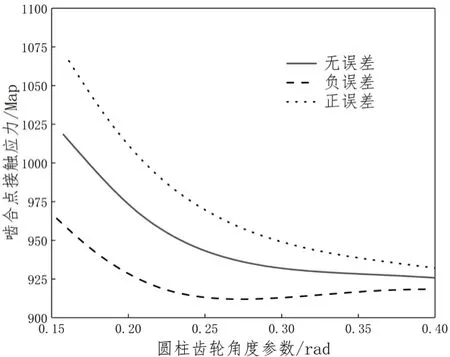
圖14 軸交角誤差對最大接觸應力的影響

由圖15～圖16可知，當軸交錯誤差與軸向偏移誤差為正時，最大接觸應力小于正常接觸應力；當軸交錯誤差與軸向偏移誤差為負時，最大接觸應力大于正常接觸應力。

圖15 軸向偏移誤差對最大接觸應力的影響

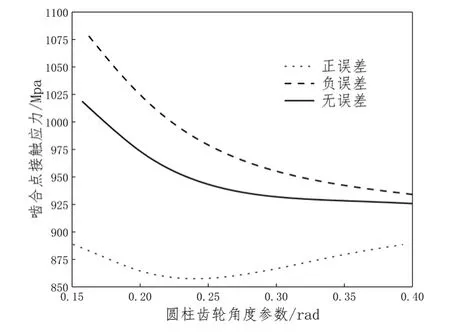
圖16 軸交錯誤差對最大接觸應力的影響

5 結語

建立了弧線齒面齒輪嚙合坐標系，分別推導了弧線齒圓柱齒輪齒面方程與弧線齒面齒輪齒面方程，得到了齒面可視化，并且通過建立正交弧線齒面齒輪副的模型，驗證了齒面推導的正確性。

建立了含三種安裝誤差的弧線齒面齒輪嚙合接觸坐標系，對接觸軌跡與接觸應力進行了分析，得到三種安裝誤差均會影響接觸軌跡位置與接觸應力大小，其中軸交角誤差影響最為顯著，應避免軸交角誤差；適當的選取軸交錯誤差與軸向偏移誤差可增加弧線齒面齒輪副的承載能力。