一種基于數據融合的目標跟蹤方法

顧保國，陳 陽

(1.中國人民解放軍63726部隊，銀川 750004；2.華東電子工程研究所，合肥 230088)

航天測控技術發展日新月異，目標跟蹤作為航天測控核心功能之一，也相應地越來越復雜。在目標跟蹤應用中，單個傳感器(單套設備)跟蹤目標有一定的局限性[1]，為了獲取更好的跟蹤效果，常常會利用多個傳感器(多套設備)輸出的測量數據[2]，以實現目標跟蹤精度和收斂性的進一步優化[3]。在測控任務中，利用雷達、光學設備等多種外部設備的測量數據來引導相控陣波束進行目標跟蹤，以期達到更好的跟蹤效果，相關文獻研究表明，組網雷達系統的檢測與跟蹤性能比單部雷達顯著提升[4-6]。

通常，測控設備接收到的引導數據受到網絡或環境影響，經常出現數據跳大數或時延抖動，同時在過頂跟蹤時受到引導信息動態滯后等因素影響，因此有必要將多設備源發送的引導數據結合自跟蹤獲得的測量信息，進行數據融合處理。數據融合可以利用多個或多種體制的傳感器所提供的冗余信息和互補信息[7]，從而提高融合后目標信息的質量[8]，減少測量信息的模糊性和不確定性，避免因自身自跟蹤或外部引導數據出現的各種異常造成對目標預測影響，提高目標的跟蹤能力[9]。但傳統的數據融合方式是根據經驗對各種測量數據賦予固定的權值，不能準確反映外部引導數據質量的變化，雖然在一定程度上提高了目標跟蹤能力，但仍然存在比較大的跟蹤誤差。為了提高相控陣雷達波束的跟蹤性能，筆者提出一種基于多源數據融合的目標跟蹤方法，將各數據源輸入的引導數據通過外推時延修正、檢擇處理、野值剔除、坐標變換、平滑濾波后，實時根據測量方差進行權值的自適應動態分配，預測目標下一周期的俯仰角和方位角，并引導跟蹤波束進行波束切換，從而完成相控陣波束的目標跟蹤，仿真實驗結果表明，所提算法相對于傳統的跟蹤算法，顯著提高了波束的跟蹤預測性能，增強了系統的可觀測性和可靠性。

1 數據預處理

1.1 處理流程

圖1描述了多源數據融合的數據處理流程圖。整個處理流程采取“分布式預測+集中式融合”架構，計算系統通過網絡或串口接收各數據源的數據，然后開啟多個線程對各數據源的引導數據進行外推時延修正、數據檢擇、坐標變換(將各自坐標系轉換到地心地固坐標系)、平滑濾波。將濾波后的估計結果加上自身設備的自跟蹤預測值傳送到數據融合模塊，完成數據融合，并輸出最終的融合結果來引導波束進行跟蹤。

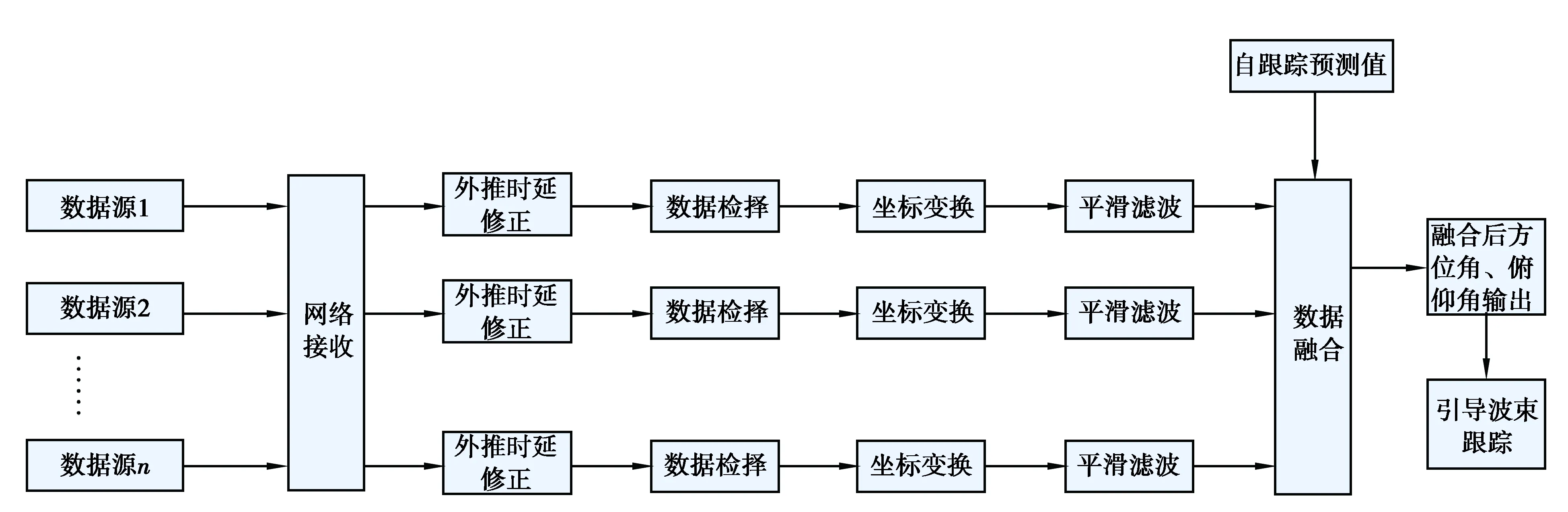
圖1 多源數據融合處理流程圖Fig. 1 Flow chart of multi-source data fusion processing

1.2 外推時延修正

由于各數據源的測量值是在各自的時間基準下進行的，再加上網絡或者串口的傳輸時延，匯聚到計算平臺的各數據源的測量數據和計算平臺本地時間必然存在一定的時間差，并且由于UDP傳輸過程偶爾會造成網絡丟包，造成測量數據丟失或中斷，因此各種引導數據的測量時序是異步的。為了使得各數據源數據在融合之前具備統一的時間基準，需要對各數據源所測量的異步數據同步到同一處理時間節點上。數據外推時延修正是進行數據融合處理的前提，其處理精度關系到后續目標的捕獲跟蹤連續性[10]。由于不同的外部所發送引導數據頻率不統一，有的設備頻率較高，有的設備頻率較低，通常情況下，通過線性插值(或線性外推)將一方配準到另一方的觀測時刻，時間配準原則是將數據率較低的一方配準到數據率較高的一方。令Tr為待處理的時間節點，Ar為待處理時間節點觀測異步數據的數據項。Ti，Ti+1為待處理時間節點最鄰近的2個時間節點，Ai，Ai+1為待處理時間節點最鄰近的2個時間節點所對應的數據項，按式(1)對其進行內插或外推時間配準處理，保證待融合的數據時間間隔相等。

(1)

1.3 數據檢擇

各數據源的引導數據會存在一定的野值數據，需要對引導數據的相關測量數據進行數據檢擇處理，保證后續處理精度。利用最小二乘法對測量數據進行預報，通過與相應的測量值進行對比，將測量數據殘差與預先確定的野值檢測門限做對比并進行檢測。大于所設置檢測門限的測量值判定為野值。

數據檢擇模型采用四階差分檢驗法進行檢驗[11]，步驟如下

1)用四階差分檢驗法式(2)對初始的五幀數據進行初始檢驗，找出一組合理點

Δ4yj=yj-4-4yj-3+6yj-2-4yj-1+yj(j≥5)，

(2)

取門限值M1(經驗值為17σ，σ為測量數據的精度)，判斷|Δ4yj|≤M1是否成立，若是，則認為這5幀數據無異常點；否則，令j=j+1繼續進行四階差分檢驗。

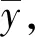
(3)

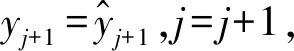
圖2以外部引導數據的俯仰角度為例，展現了數據檢擇的效果。可以看出數據檢擇能將測量過程中的幾個跳點很好地剔除，和原始數據相比也保證了檢擇處理后數據基本在真實數據附近，避免了異常值引入帶來的風險。

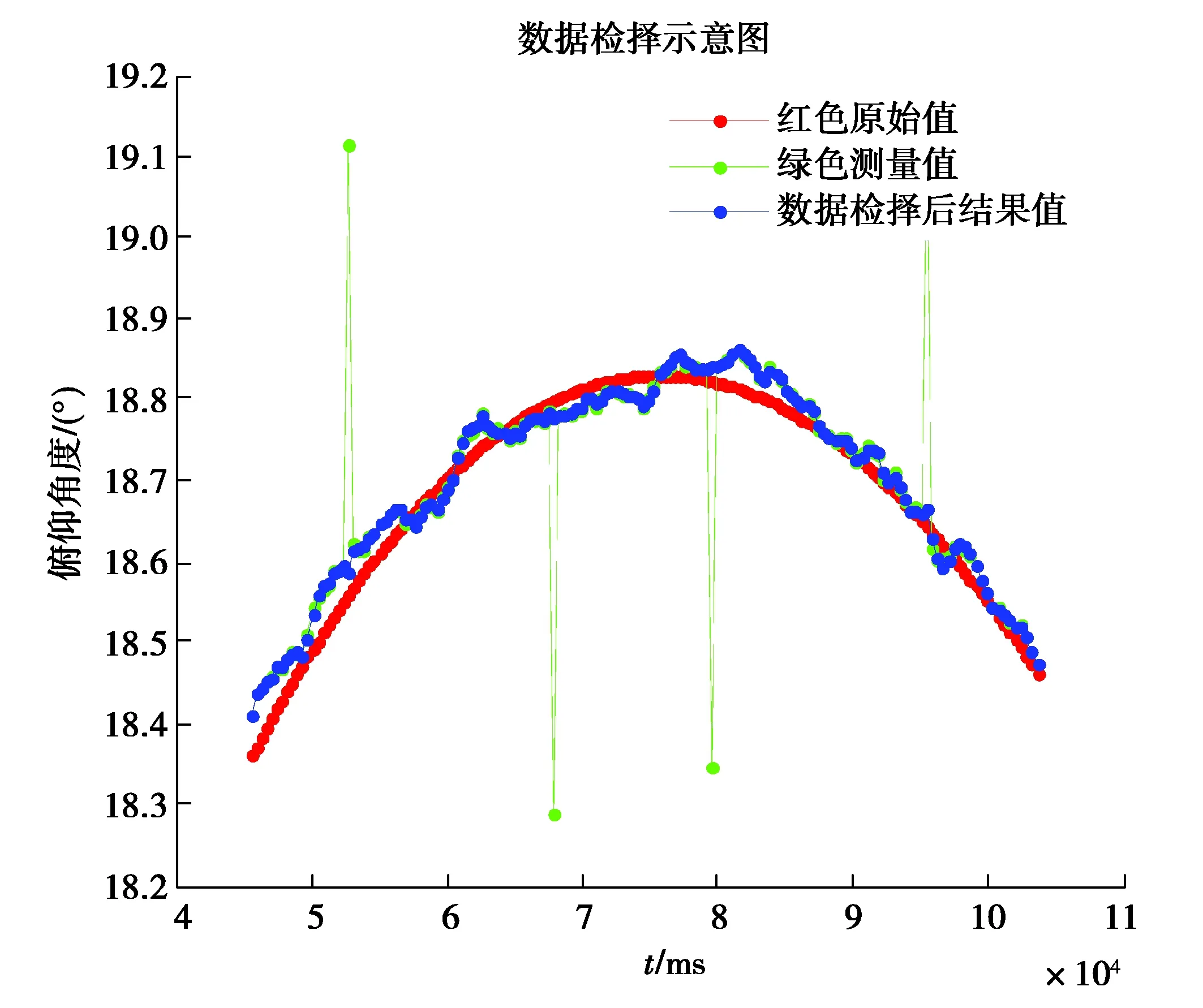
圖2 數據檢擇效果圖Fig. 2 Effect chart of data selection

1.4 坐標變換

由于外測設備傳送的數據是在地心坐標系下的位置或者是經度、緯度和高程，比較特殊額的是同站設備，它的引導數據是測站系下的位置，而自跟蹤數據是陣面坐標系下的測量值。同一波束指向通常是相對于陣面坐標系的，為了描述同一個目標的位置屬性，保證融合坐標系的統一，需將目標觀測數據轉換到同一坐標系、同一量測單位[12]，即陣面坐標系。坐標轉換如圖3所示。如果是運動平臺，則要將平臺的位置姿態信息(經度、緯度和高程)先轉換地心地固坐標系，再轉化到東北天坐標系獲得姿態角。地心地固坐標系下的目標位置結合姿態角轉換到平臺坐標系下的位置，再轉化到陣面坐標系下的位置和極坐標下的角度。如果引導數據是經度、緯度和高程信息，則要先轉化地心地固坐標系。

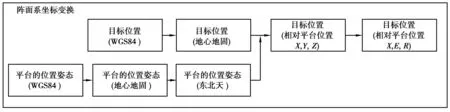
圖3 坐標轉化圖Fig. 3 Coordinate transformation diagram

1.5 平滑濾波

經過上述坐標轉化后獲得目標在陣面坐標系下的方位角和俯仰角測量值的離散點序列yi。為了保證測量值的平滑性，采用七點3次平滑法[13]的 式(4)對采集到的測量數據進行離散值平滑。

(4)

如果數據源事先知道其軌跡位置，則可以根據式(4)平滑7個時刻點的方位角和俯仰角，然后將其送入數據融合模塊和自跟蹤數據進行融合處理；如果數據源為實時發送的數據，則剛開始的7點利用原始值進行融合，后面的數據則利用式(5)根據平滑后的值進行外推。

(5)

其中η1+η2+η3+η4+η5+η6=1。通常離最新引導數據最近的點對于預測貢獻值較大，所以取η1>η2>η3>η4>η5>η6。

2 數據融合

通過數據融合，有效利用不同數據中的信息，可提高目標跟蹤精度[14]。由于目標的真實運動軌跡未知，將各數據源的引導數據、自跟蹤數據的測量信息的中心點看作目標真實運動軌跡的參考點，各測量信息與參考點的偏差看作是目標運動軌跡的偏差。利用統計理論計算出各測量信息與參考點偏差的標準差,這里之所以不用平均偏差而用標準差，是因為平均偏差給出的平均值比實際平均偏差大[15]。以標準差作為數據融合精度近似,并以該近似值分別計算出數據融合加權平均合成時各測量信息的權值。

假設在數據融合時刻Ti，經數據預處理得到的引導數據或自跟蹤數據中的方位角/俯仰角信息為Ai,m，m為數據源的數量。則數據融合時刻Ti的測量方程為[16]

Ai,m=Xi,m+Vi,m，

(6)

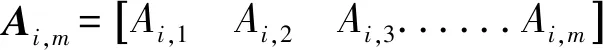
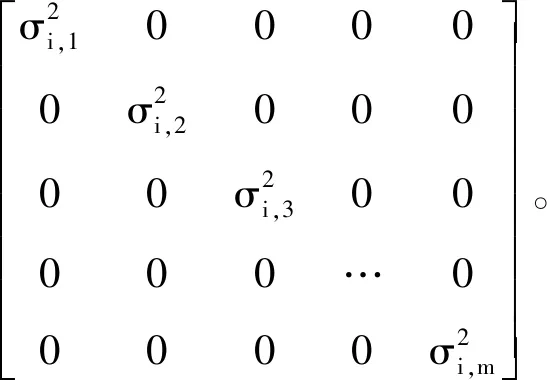
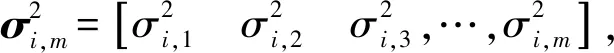
建立加權估計誤差方差表達式[17]

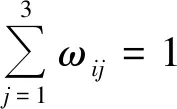
依次對加權因子求取偏導，聯立求解可得

在Ti時刻，確認是對同一目標的測量數據，可利用加權最小二乘估計進行合成[18]。輸出Ti數據聯合處理后的目標測量數據。

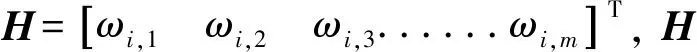
3 仿真分析與實驗

3.1 精度對比

利用仿真實驗驗證了目標跟蹤方法的正確性。以3種數據源作為輸入，包括引導數據1(測站坐標系下測量數據)、引導數據2(地心大地坐標系下測量數據)和自跟預測值，數據采樣周期1次/s。經過融合后的目標俯仰角跟蹤結果如圖4所示。從結果可以看出，融合后的俯仰角和真實的角度幾乎重合，而自跟預測值和真實值之間誤差大于融合后的誤差，融合跟蹤與真實值的偏差較自跟預測值與真實值的偏差降低了80%以上。這說明單一利用引導數據源1或數據源2，或自跟蹤預測值，對目標的跟蹤精度顯著低于融合后的跟蹤精度。圖5為提出的方法與文獻[10]所提出方法的比較也驗證了所提出的融合方法的有效性。

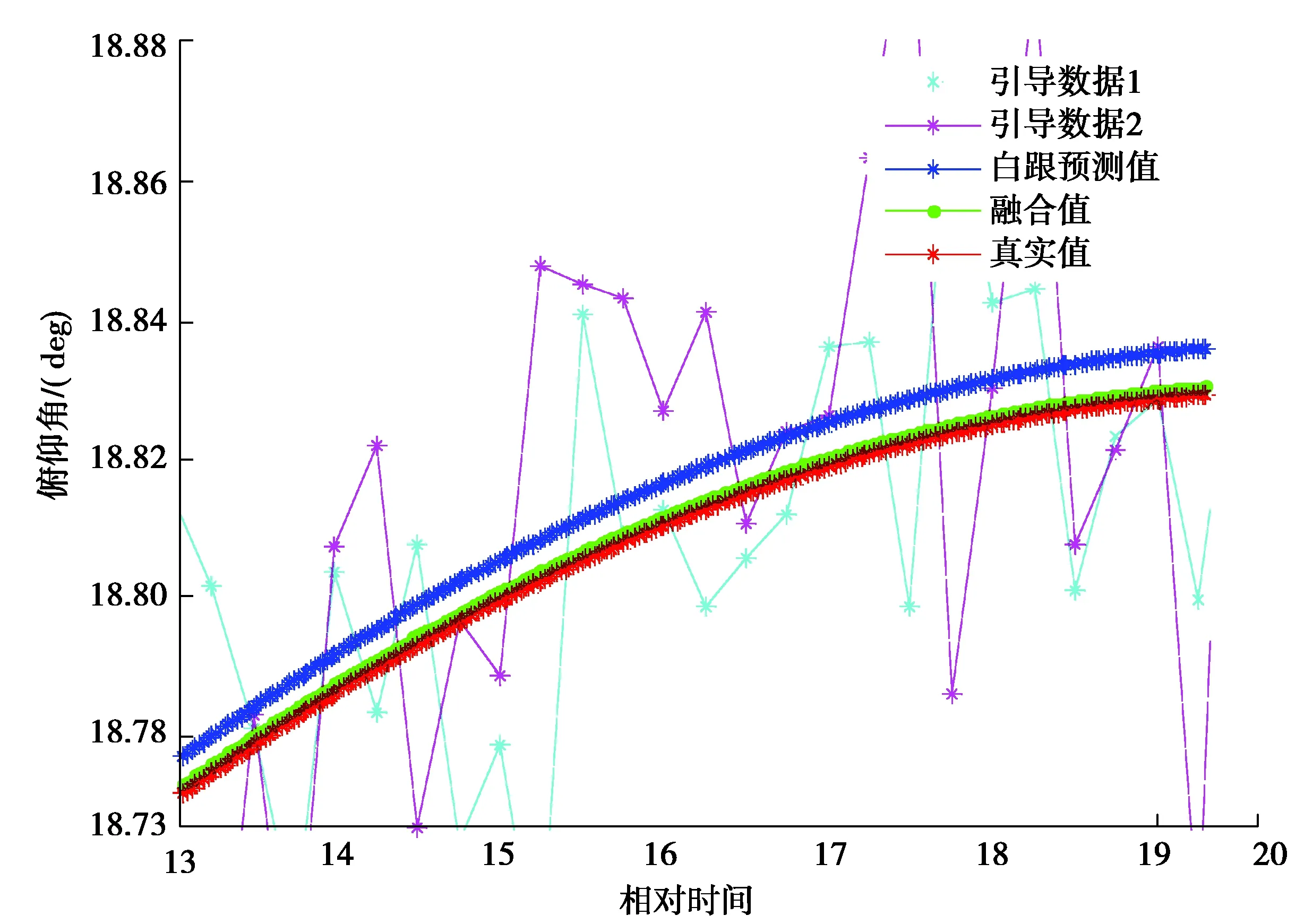
圖4 研究方法的跟蹤結果圖Fig. 4 Tracking results of the method in this paper

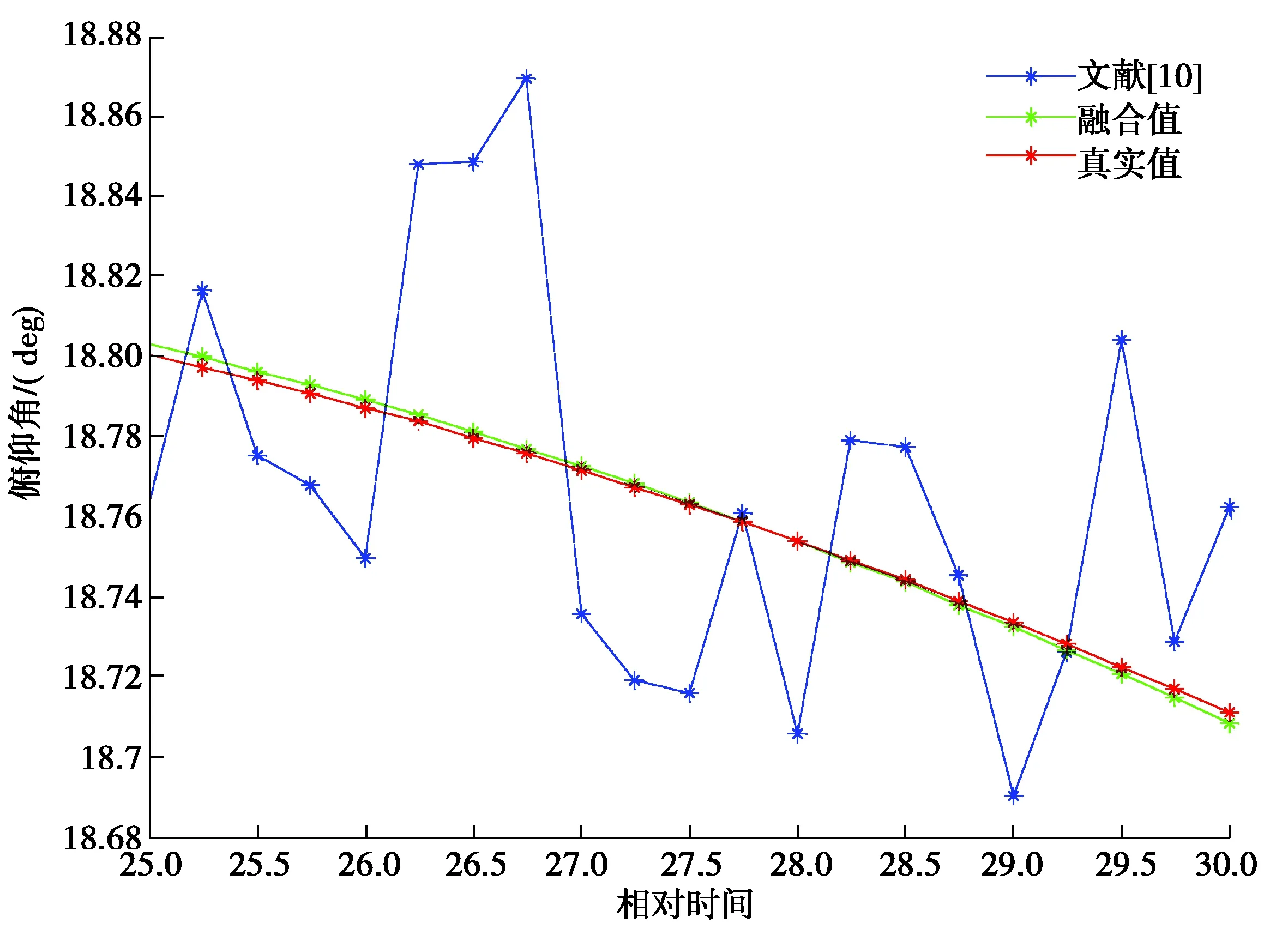
圖5 與文獻[10]的方法比較Fig. 5 Comparison with the method in reference [10]

3.2 時間代價對比

將所提出的算法與文獻[10]中的方法以及未采用融合跟蹤處理的算法進行對比，選取同樣一組數據(100幀)作為輸入數據，在同樣軟硬件環境下進行仿真運算，3種算法的運算耗時分別為1.125 ms、0.013 ms和0.002 ms，雖然算法耗時遠高于另外2種(分別是另外2種算法的86倍和562倍)，但仍然遠小于跟蹤與伺服控制計算機的主線程周期(主線程周期一般12.5 ms，即80 Hz)，不會對天線的跟蹤控制造成任何不利影響，完全可以接受。

4 結 論

為了解決目標在相控陣波束下的有效跟蹤的問題，利用多設備源采集的引導數據、自跟蹤數據的測量信息，進行數據融合處理，提出了一種基于動態權值分配的數據融合跟蹤方法。與傳統的僅利用自跟蹤數據進行目標波束跟蹤相比，所提方法在付出時間代價可接受的情況下有效提高了僅依賴單一設備源的數據的跟蹤精度，值得注意的是，討論數據融合的目標跟蹤方法是基于多設備源均能獲取相應的測量信息，在實際的目標波束有效跟蹤工程實現時，將該方法作為目標波束有效跟蹤輸出的一種策略。實際策略自適應切換所應滿足的條件，將是下一步重點研究的內容。