NO 分子形狀共振阿秒動力學精密測量*

徐一丹 姜雯昱 童繼紅 韓露露 左子潭 許理明 宮曉春? 吳健?

1) (華東師范大學,精密光譜科學與技術國家重點實驗室,上海 201100)

2) (華東師范大學化學與分子工程學院,上海 201100)

形狀共振是分子電離散射過程中的一種重要現象,其阿秒量級的光電離延時的精密測量,是深入認識形狀共振過程及成因的重要基礎.本文使用基于近紅外飛秒激光與極紫外阿秒脈沖串的阿秒符合干涉儀,利用雙光子干涉的阿秒拍頻重構的探測方法,對一氧化氮(NO)分子4σ 電子的形狀共振過程進行研究,實驗測量了分子內有效電離延時對光子能量的依賴關系,通過對比雙光子躍遷延時與單光子躍遷延時,發現單光子過程的Wigner 延時是雙光子躍遷延時隨能量變化的主要原因.基于單中心展開的量子散射理論計算表明,在分子形狀共振位置的電子電離延時,主要由連續態中高角動量離心勢囚禁的電子決定.

1 引言

在光與物質的相互作用中,當處于基態的中性原子或分子吸收的光子能量大于其電離能時,中性原子或分子體系會失去電子,產生正離子碎片及連續態光電子,為探索微觀物質結構及動力學提供重要探測途徑.與飛秒時間尺度原子核波包轉動[1]、分子化學鍵斷裂[2]、分子內電子-原子核關聯[3]動力學過程相比,電子的運動發生在極小的空間尺度與極短的時間尺度(10—18s)上,需要阿秒時間分辨的精密測量手段.近年來,聚焦于電子超快動力學的阿秒精密測量技術,已經被應用于探測原子分子電離延時[4-7]、化學鍵斷裂[8]、電荷轉移[9]等過程.

分子形狀共振于1935 年由Fermi 等[10]首先在人工放射性慢中子捕獲實驗中發現,此后,一直是物理、化學、生物領域研究的熱點問題,例如放射性核衰變[11]、超冷碰撞[12]、低能電子散射[13,14]、DNA 輻射損傷[15]等.在光致分子電離的過程中,電子的動力學過程如圖1 所示,具有一定動能的自由電子被離心勢壘短暫捕獲,等效于實驗觀測到的電子隧穿通過原子核勢壘導致的百阿秒量級的電離時間延時.同時,在共振能量附近,分子光電離散射截面出現顯著共振增強峰,上述共振壽命與能量取決于束縛電子的勢壘形狀,因此得名“形狀共振”,進一步的研究表明在共振能量點,出射光電子的角分布不對稱參數有明顯的下降[16,17].

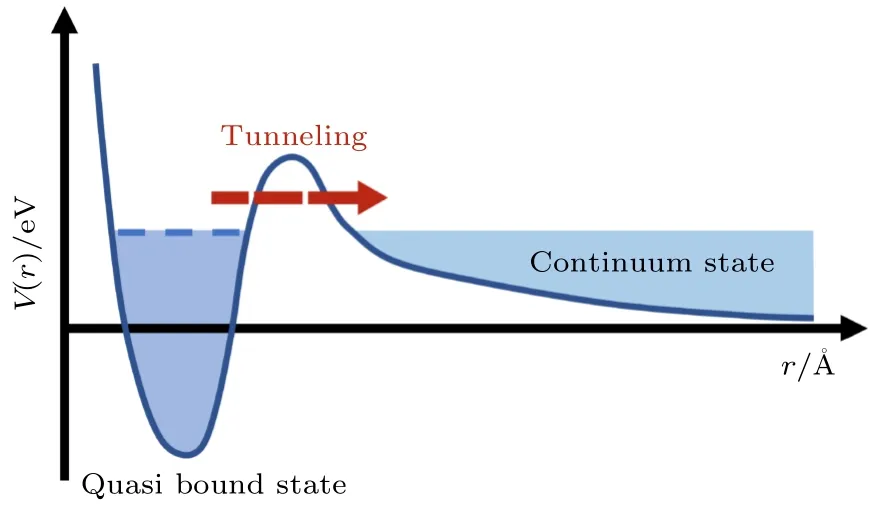
圖1 形狀共振中電子隧穿過程示意圖.藍色曲線為電子感受到的隨電子到原子核距離r 變化的離心勢場.電子發生形狀共振時,可被離心勢壘短暫束縛,之后隧穿進入連續態Fig.1.Schematic illustration of the electron tunneling process in shape resonance.The blue curve indicates the centrifugal potential of the electron as a function of the distance to the nuclei.During the shape resonance process,the electron is temporally trapped by the centrifugal potential barrier,and then tunnels into the continuum state.

近幾年,極紫外阿秒光脈沖產生技術的發展,極大地推進了阿秒尺度電子極端超快動力學精密測量的實驗研究,例如基于極紫外阿秒脈沖和近紅外飛秒脈沖的雙光子干涉的阿秒拍頻重構 (reconstruction of attosecond beating by interference of two-photon transitions,RABBIT)[18]方法可以被用于測量形狀共振中電子電離的延時動力學.2016年Huppert 等[5]利用RABBIT 方法研究了N2O 分子的形狀共振過程,測得態與態之間存在160 as 的光電離延時,在21.7—37.2 eV 光子能量范圍內存在σ對稱與 π 對稱的形狀共振,其中σ對稱的形狀共振對分子光電離延時有顯著影響,與相關的σ共振能量為28.8 eV,共振壽命為114 as,而與態相關的σ共振能量在25.5 eV,共振壽命為97 as[5].2020 年,Nandi 等[4]利用RABBIT 方法研究了N2分子的形狀共振過程,發現分子振動影響核運動,使勢壘發生微小變化,造成光電子出射延時改變達200 as,證明Franck-Condon 圖像在光電離動力學中的局限性,即電子躍遷不能當作相對于原子核的瞬時運動.2021 年Heck 等[19]研究了CF4分子HOMO 和HOMO-1 軌道的不對稱電離延時,將這種不對稱性的原因追溯到共振時主要有2—3 個分波占主要貢獻.2022 年Ahmadi 等[20]同樣研究了CF4分子,發現出射光電子所受的分子勢取決于發射方向,不同高度的勢壘導致了各向異性的時間延時;CO[17],NO[21,22]等分子利用阿秒技術的探測工作也陸續開展,實現了電子隧穿延時的精密測量.

NO 分子中存在多個電子態相關的形狀共振過程,對理解分子形狀共振具有重要意義.1981 年,Wallace 等[23]通過理論預測了NO 分子σ 光電離通道中的形狀共振現象,并討論了原子核運動對光電離截面與光電子角分布等觀測值的影響.近幾年,Suzuki 等[24]利用time-energy mapping 表征了NO 分子的空間電離動力學,利用?分波軌道雜化方法解釋了電離動力學中的相位與量子缺陷之間的差異;高次諧波光譜和強場電離也用于研究NO 耦合的電子波包,發現在光子能量14 eV 附近處,NO 分子的自電離與形狀共振的存在極大改變了偶極矩的角度分布[25].Veyrinas 等[26]利用同步輻射光源,研究了光子能量在23—33 eV 范圍內NO+C3Π 電子態的形狀共振光電子動力學,發現對稱性為Π 和Σ 的NO+電子態動力學行為有明顯區別.

電子波包在分子形狀共振附近的電離延時,即形狀共振的壽命相關的測量工作陸續開展.然而,這些電離延時測量都是在分子軸方向上取角度平均值[4,5]、對比平行躍遷和垂直躍遷情況[27],或探測定態的光電子角分布[17,21].分子形狀共振的角分辨延時測量,特別是RABBIT 實驗方法中的雙光子電離延時與單光子吸收電離的Wigner 電離延時之間的相對關系,仍然是一個有待探討的問題.

本文結合阿秒極紫外光源和電子-離子符合探測系統,對NO 分子 4σ→σ*形狀共振過程進行研究,通過基于RABBIT 實驗采集的Ar 原子、He 原子、NO 分子的光電子譜進行相位提取,得到出射光電子的有效延時對入射光子能量的依賴關系,進一步探究了雙光子過程光電離延時與單光子延時、連續態傳播躍遷延時之間的關系.理論計算得到形狀共振過程初、末態電子波函數軌道,討論了其分子形狀共振雙光子電離延時與單光子電離延時之間的聯系與區別,并且發現f分波對該形狀共振起主導作用.

2 阿秒符合干涉儀

2.1 阿秒電子離子三維動量符合測量

如圖2 所示,實驗中使用Ti:sapphire 激光器產生近紅外飛秒脈沖(near-infrared femtosecond pulse,NIR),中心波長為790 nm,激光脈寬28 fs,脈沖功率為1.6 mJ,重復頻率為10 kHz.飛秒脈沖通過分束鏡后,其中一束光通過內部充滿惰性氣體氬氣的光纖波導裝置[28],基于氣體高次諧波原理[29,30]產生極紫外(extreme ultraviolet,XUV)阿秒脈沖串,產生的高次諧波主要覆蓋15 級到23 級,對應的光子能量為23.85—36.57 eV.產生極紫外脈沖串后采用厚度為100 nm 的鋁箔將XUV 中的NIR 部分濾掉,并通過鍍金環面鏡進行聚焦(f=50 cm).極紫外阿秒脈沖與近紅外飛秒脈沖兩路光構成馬赫-曾德爾干涉儀,泵浦探測光路的相對光程,由時間精度在阿秒級壓電陶瓷電機主動伺服反饋控制系統實時調節,精確操控泵浦探測光之間的相對延時.

圖2 泵浦探測實驗光路示意圖,泵浦光為高次諧波產生的極紫外阿秒脈沖串(XUV-APT),探測光為NIR,兩路光分別聚焦后作用在COLTRIMS 中的超聲分子束上產生正離子碎片與電子Fig.2.Schematic diagram of the pump-probe experiment.The pump light is extreme ultraviolet attosecond pulse train (XUV-APT) generated by high-order harmonics generation process,and the probe light is NIR.Positive ion fragments and electrons are generated on an ultrasonic molecular beam in COLTRIMS.Two beams are focused respectively and reach on the ultrasonic jet in COLTRIMS to generate positive ion fragments and electrons.

此外,實驗系統還包括冷靶反沖動量譜儀(cold target recoil ion momentum spectroscopy,COLTRIMS)[31].該系統具有三維動量測量、4π 空間立體角碎片收集、電子-離子多體符合測量的功能.XUV 與NIR 分別聚焦共同作用在COLTRIMS中的超聲分子束上,產生的離子碎片與電子在譜儀內部的勻強電場和磁場作用下分別到達位于真空腔體兩端的離子探測器和電子探測器,帶電粒子打在探測器上的位置可以通過MCP 與延時線裝置被精確確定,再根據帶電粒子在譜儀中的飛行時間,就可以重構出探測到的每個粒子的三維動量,獲得反應體系內每個粒子的動量、能量信息.

2.2 RABBIT 原理

RABBIT 方法是探測阿秒尺度電子超快電離動力學的主要方法之一.利用XUV-APT 作為泵浦(pump)光,NIR 為探測(probe)光,電子首先吸收單個XUV-APT 光子從初態躍遷至連續態,同時吸收或放出一個NIR 光子,產生含有主級次峰 (main peak) 與邊帶 (sideband) 的光電子能譜,其中邊帶電子來自具有相同能量的兩種電離路徑之間的干涉,即吸收第q— 1 級XUV-APT 光子后再吸收一個NIR 光子電離的電子波包,與吸收第q+1 級XUV-APT 光子后釋放一個NIR 光子電離產生的電子波包之間的干涉(圖3).邊帶信號隨泵浦探測延時的改變發生周期性強度變化,邊帶光電子譜強度的變化頻率為NIR 光載波頻率的2 倍.而邊帶電子信號的振蕩相位,攜帶包含了阿秒脈沖啁啾、光電子出射時短程庫侖相互作用產生的延時和電子傳播過程中長程庫侖與激光場耦合相互作用產生的延時等信息[32-35].

圖3 RABBIT 原理示意圖.左圖為實驗采集的氬原子阿秒光電子能譜,右側為抽運探測時間積分后的光電子能譜,包含主級次電子和邊帶電子.邊帶電子通過從第q— 1 級和第q+1 級主級次電子分別吸收和釋放一個NIR 光子產生的兩條量子躍遷路徑干涉產生Fig.3.Schematic diagram of RABBIT method.The left figure shows the experimentally measured attosecond photoelectron spectrum of argon atoms.The pump-probe time delay integrated photoelectron kinetic energy distribution is shown in the right panel including the main peaks and sidebands. The qth sideband electron is generated via the quantum interference between the pathways populated via the single NIR photon absorption and emission from the main peaks of the (q— 1)th and (q+1)th order.

2.3 光電子輻射電離延時

由于量子力學中并沒有表示時間的厄米算符,要描述光電離過程中電子波包的時間延時,首先需要引入由Eisenbud,Wigner 和Smith[32,33]建立和推導出的散射相移,這種相移可以看作是散射電子波包與未受擾動電子波包之間的群速度延時,Eisenbud-Wigner-Smith (EWS)延時τEWS可表示為粒子傳播時被散射勢賦予的相移的能量導數,對角動量量子數為l的單個分波,其延時可表示為

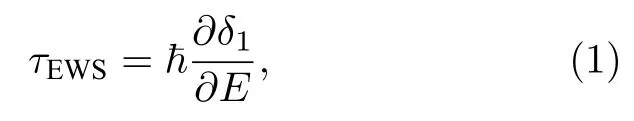
其中δ1為散射勢,E為電子波包的能量,? 為約化普朗克常數.而光電離可以描述為從勢中心開始的半散射過程:

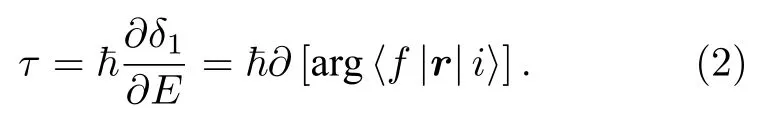
采用RABBIT 實驗方法探測分子光電離過程,當XUV 場與IR 場均為線偏振且偏振方向相同時,采集的光電子邊帶強度存在關系:

其中M(2q±1)代表 2q±1 級邊帶電子的雙光子躍遷矩陣元,正(負)號表示吸收(釋放)一個NIR 光子.邊帶相位延時對應的延時可以表示為

通常情況下,分子雙光子電離延時可以寫成兩項之和:

其中τcc項不包含分子內部信息,可以用連續態傳播躍遷延時解釋,由近紅外光場頻率、靶離子庫侖勢場與光電子釋放動能決定.τmol(2q)項為與分子勢能信息相關的時間延時,但與單光子電離延時τ1hν并不相等,因此分子體系中測得的雙光子躍遷時間延時不能像原子體系一樣,簡單拆分成單光子躍遷延時τ1hν與連續態傳播躍遷延時τcc(2q)之和.

2.4 單中心展開量子散射計算

為了進一步從分波的角度,理解分子形狀共振的性質和由此產生的電離延時,利用NO 分子質心處散射分波進行了單中心展開的量子散射計算[36,37].分子的電子結構采用Hartree-Fock 近似處理,初態和末態電子波函數通過分子質心處的單中心分波展開:

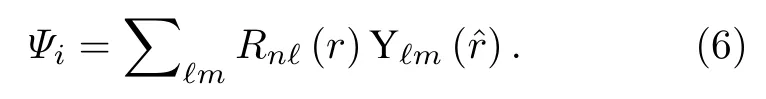
該展開由n=N/2 個占據軌道的反對稱乘積構成,使用ePolyScat 實現[36,37],采用的最大角動量分波?max=60.在長度規范下,線偏振光作用下的光電離偶極矩陣元可以表達為

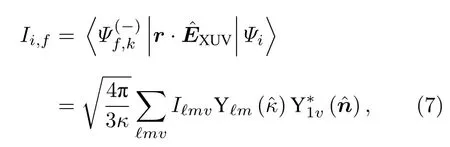
由于在實驗室坐標系下,分子取向隨機排列,無法提取相對于分子軸的各個發射方向上的電子電離延時,所以探測到延時分布是分子取向、發射方向平均的結果,而分子坐標系下的光電子角分布則有更豐富的結構,并且可以獲取散射光電子分波分辨的振幅和相位值,進而獲得相對于分子軸方向的角度分辨的光電子電離延時.在分子取向固定時,分子坐標系內光電子延時隨發射角的關系可表示為:

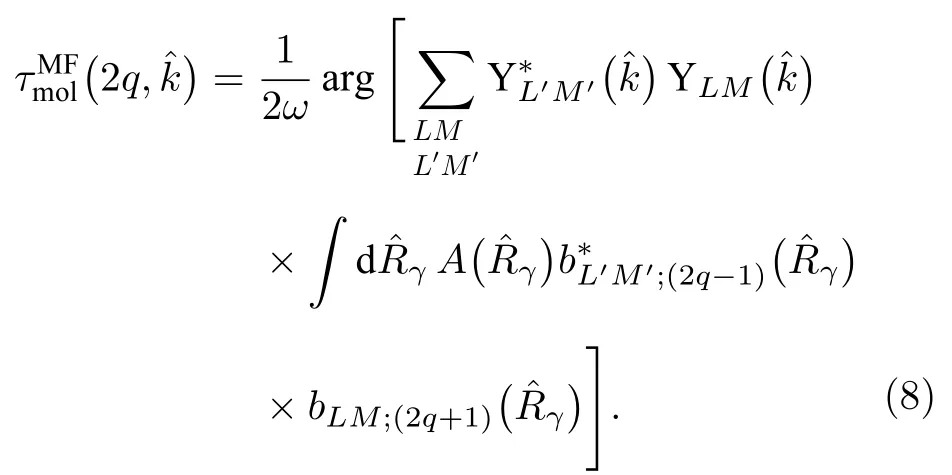
在實驗室坐標系下測量到的無角度分辨的雙光子電離延時,是所有分子取向和光電子發射角平均后的結果,可以表示為

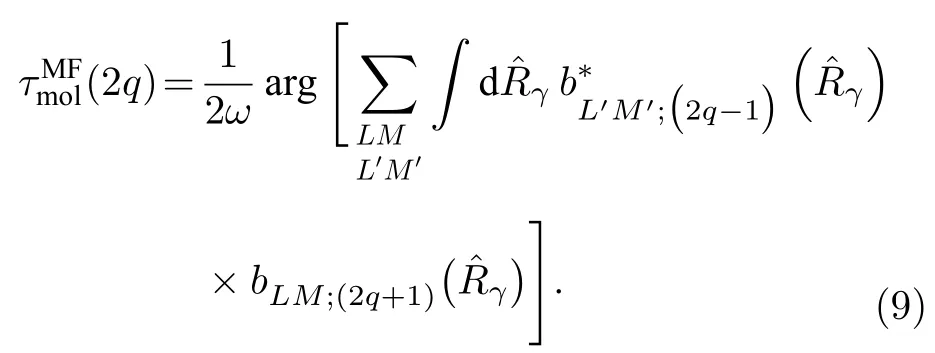
光電離截面是光電離動力學研究中的一個特征參數[38],光電離截面在某一能量區域內快速增大是共振在實驗上的顯著特征,因此在形狀共振中被廣泛研究,由(8)式得出散射截面與光電子能量E的關系可以表示為

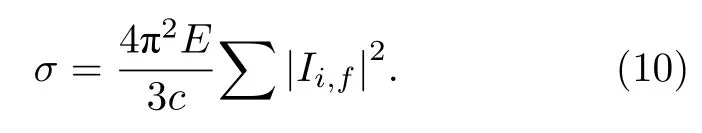
對于分子體系,當線偏振光與物質相互作用時,單光子電離的光電子角分布的一般表示[39]為

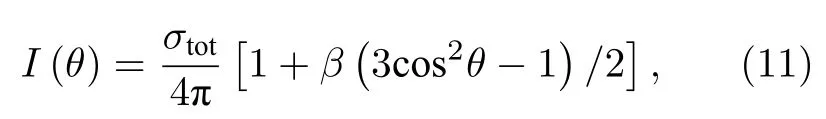
其中,θ為光電子發射方向與線偏光偏振矢量之間的夾角,β稱為不對稱參數[40],取值為—1—2.不對稱參數β可由Cooper-Zare 方程計算得:

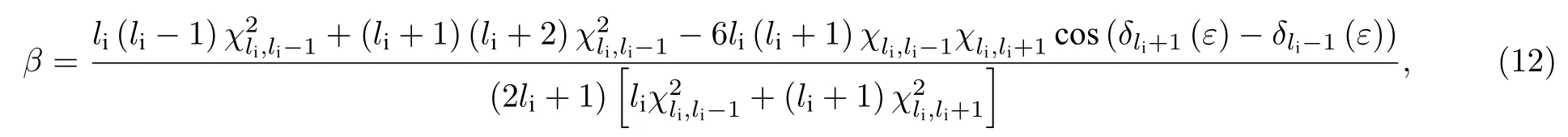
其中,li是初態軌道角動量量子數,為偶極躍遷允許的自由電子分波的徑向矩陣元,l=li±1,是相互作用引起的相移.由(12)式可得,不對稱參數β對能量的依賴關系主要由余弦項決定,其變化主要取決于相移隨能量的變化.同時,β也取決于躍遷矩陣元的相對比例.

3 結果與討論

本文研究的NO 分子 4σ→σ*形狀共振過程,發生在4σ內殼層電子受到光激發后產生 c3Π NO+態,產生NO+離子態的電離勢為Ip=21.73 e,之后解離產生N+和O 離子碎片,由于電子電離路徑在相似電子動能處存在多個離子態,通過電子離子符合測量可以精確篩選出 c3Π 離子態對應的離子動能范圍[26],從而在實驗上篩選出來自4σ軌道上的光電子.從4σ軌道上電離的光電子對應的N+離子動能約為0.45 eV,實驗上選出動能 0.4 eV＜＜0.5 eV 的N+離子信號,對應的電離解離路徑為

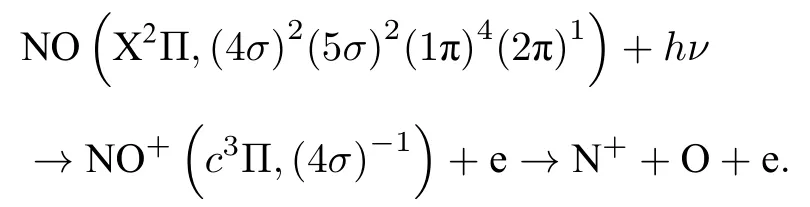
使用ePolyScat 進行基于迭代Schwinger 變分原理的量子散射計算,得到 4σ→σ*形狀共振過程的基態電子波函數分布,及共振態電子波函數分布,分別如圖4(a),(b)所示,其中N 原子核位于z≈0.60 ?,O 原子核位于z≈—0.55 ?.光電離振幅、延時等分布的不對稱性與初態、末態電子波函數分布的不對稱性緊密相關,且不同分子的形狀共振過程中,不對稱延時的來源并不相同,例如CF4分子形狀共振中的不對稱延時的來源是末態[19],而CO 分子的不對稱延時則由初態決定[27].如圖4 所示,在NO 分子中初態軌道具有更明顯的不對稱性,這種不對稱性與N,O 原子核具有不同勢分布相關,而對于計算得到的共振能量E=7.9 eV、共振寬度Γ=4.2 eV 的共振態,該共振態處于局域電勢中,比初態軌道有更高的不對稱性.

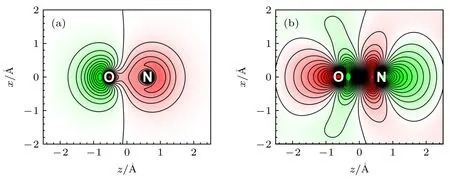
圖4 (a) NO 4σ 基態電子波函數,N 原子核位于z≈0.60 ?,O 原子核位于z≈—0.55 ?,波函數相位符號分別用綠色、紅色標記;(b) NO σ*共振態電子波函數,該共振態處于局域電勢中Fig.4.(a) Electron wavefunction distribution of NO 4σ ground state.The N and O nuclei is located at z≈0.60 ? and z≈—0.55 ?.The sign of electron wave function is marked in green and red;(b) electronic wave function distribution of the σ* resonance state,which is trapped in a centrifugal potential in the classical presentation.

圖5 呈現實驗獲得的線偏振光作用下Ar 原子、He 原子與NO 分子的阿秒光電子能譜,其中極紫外阿秒脈沖串產生光子能量主要集中在23.85—36.57 eV 的諧波,使氬原子3p 電子(電離勢Ip=15.76 eV)、氦原子1s 電子(電離勢Ip=24.58 eV)發生電離,同時,NO 分子4σ電子(電離勢Ip=21.73 eV)電離,形成15—23 級主級次峰及其間的邊帶.

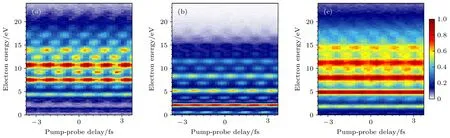
圖5 阿秒光電子能譜 (a) Ar 原子3p 電離通道(Ip=15.76 eV);(b) He 原子1s 電離通道(Ip=24.58 eV);(c) NO 分子 4σ 電離解離通道(Ip=21.73 eV)Fig.5.Attosecond photoelectron spectra of the electron released from (a) Ar atom 3p state (Ip=24.58 eV);(b) He atom 1s state(Ip=24.58 eV);(c) NO molecular 4σ orbital (Ip=21.73 eV).

為了準確提取光電子譜中邊帶信號的相位及延時信息,采用一系列高斯函數對主級次峰與邊帶延時積分后的強度分布進行擬合,之后沿延時軸進行快速傅里葉變換,通過復值擬合提取每一條邊帶的相位及振蕩強度.邊帶相位對應的電離延時包含阿秒脈沖啁啾、光電子出射時短程庫侖相互作用產生的延時、和電子傳播過程中長程庫侖相互作用產生的延時等成分.

對Ar,He 和NO 通道的RABBIT 譜進行全角度積分,擬合得到有效延時(effective delay),Ar,He 和NO 不同邊帶對應的延時變化趨勢一致,吸收光子數越多,邊帶級次越高時,延時逐漸增大,這與阿秒脈沖正啁啾理論上對延時的影響是一致的.對NO 與兩種原子測得的相同邊帶的有效延時做差,可以消除NO 的延時中阿秒脈沖啁啾的影響,將NO 分子的相對延時定義為

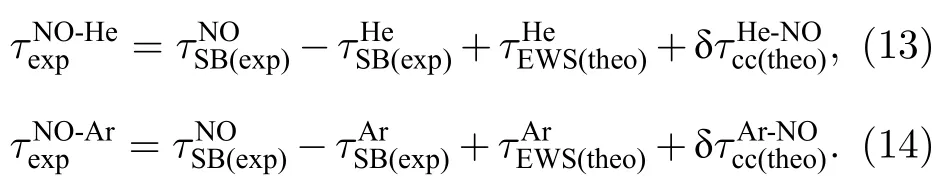
結果如圖6 中藍、綠色線所示,圖6 中的橙色線代表相同能量下計算得到的單光子延時,又稱Wigner 延時,以及計算得到的連續態傳播躍遷延時τcc.如前面所述,RABBIT 實驗提取的光電離延時對應于雙光子躍遷過程,在分子體系中并不等于單光子延時與連續態傳播躍遷延時之和.在圖中可以看出,對于NO 分子16-24 級邊帶信號,實驗上測得的單光子過程對應的相對延時,與理論計算單光子延時變化的趨勢基本相同.NO 分子與不同原子的相對延時差,來源于Ar 和He 原子本身在相同能量處有效延時的差值.連續態傳播躍遷延時τcc隨能量的增大而增大,而且受光場強度的影響,τNO-Ar,τNO-He與τ1hν能量依賴關系的差異,可能與IR 光的光強以及形狀共振電子與τcc之間的相互影響有關.

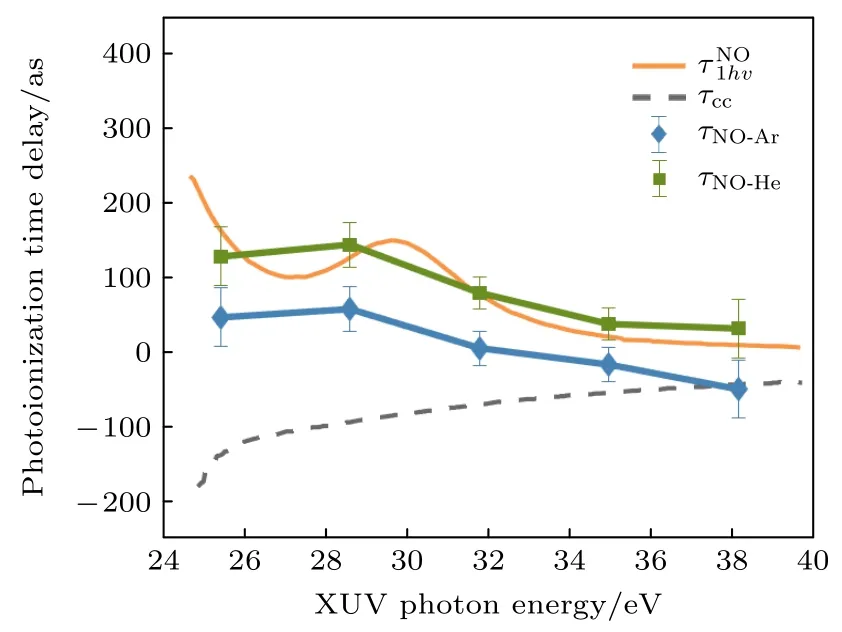
圖6 實驗測量的NO 分子有效相對光電子電離延時 τNO-Ar,τNO-He,以及理論計算單光子延時 、連續態傳播躍遷延時 τccFig.6.Experimentally measured effective photoemission time delay difference of τNO-Ar,τNO-He and theoretically calculated one-photon delay and continuum-continuum transition time delay τcc.

從時域波包演化角度看,形狀共振過程中,由于離心勢壘捕獲囚禁連續態光電子,相比于無束縛連續態電子,形狀共振電子的束縛囚禁過程表現為共振電離延時.從分波的角度理解,只有軌道角動量l＞2 的分波才能形成.利用單中心量子散射,對m=0,具有不同角動量量子數l的分波進行理論計算,得到圖7(a)所示的離心勢壘分布.對于l較小的分波通道,當l=2 時才逐漸形成微小的勢壘,但勢阱很淺,無法束縛光電子;對于l更高的分波通道,如l=4,5,勢壘高度高于45 eV 且勢阱底部接近20 eV,XUV 光子能量不足以將初始準束縛態布局到這些高角動量連續態;只有l=3對應的f分波具備對形狀共振有貢獻的勢壘形狀.

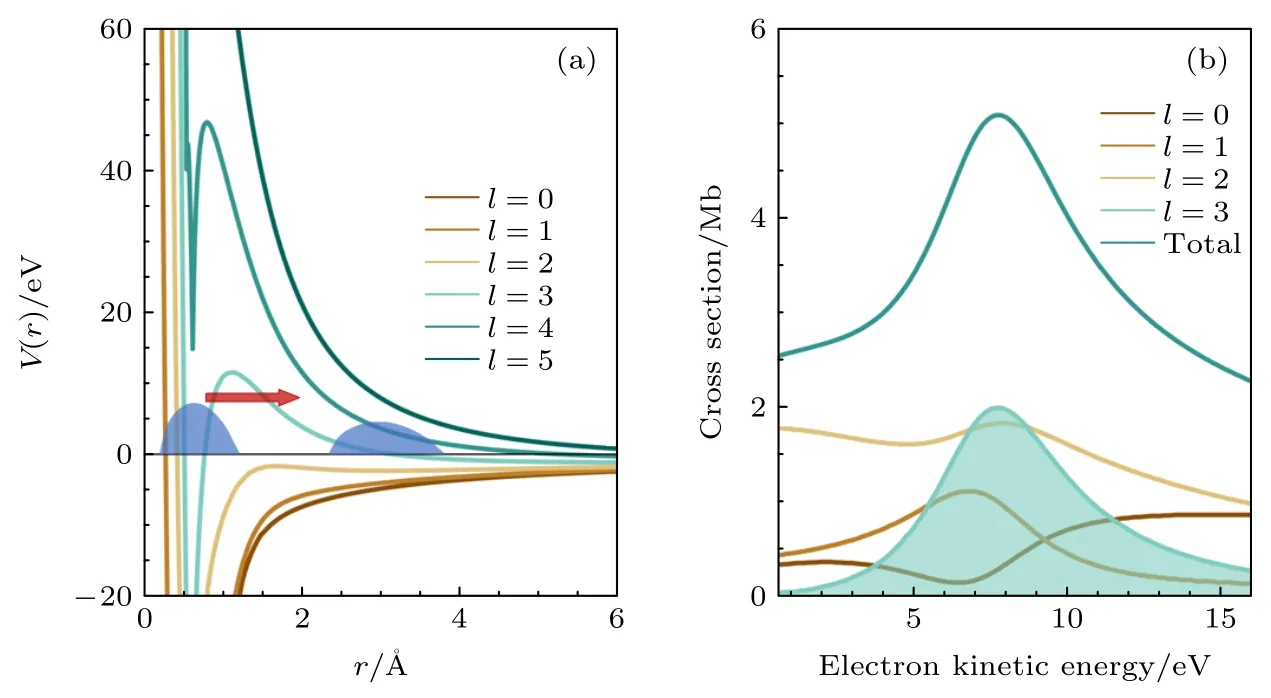
圖7 基于ePolyScat 單中心量子散射模型的單分波通道理論計算結果 (a) l=0 到l=5 的單分波離心勢壘分布,深藍色包絡為電子波包示意;(b) 不同分波通道的單光子電離散射截面隨光電子動能的變化,4σ 形狀共振共振能量在光電子動能8 eV 附近Fig.7.Partial wave resolved theoretical result based on ePolyScat calculation: (a) Centrifugal potential distribution of each partial wave channel from l=0 to l=5.The dark blue envelope represents the electron wave packet;(b) one-photon ionization scattering cross section for different partial wave channels.The 4σ shape resonance energy is centered at the photoelectron kinetic energy of 8 eV.

此外,光電離散射截面的增強效應是共振過程的顯著特征,對單個分波進行散射截面的計算,可以直觀反映不同分波通道對形狀共振的貢獻.利用單中心量子散射方法,對4σ電子的XUV 單光子電離過程進行理論計算,計算得到m=0,不同角動量量子數l分波電離通道的散射截面,如圖7(b)所示.對于所有分波通道,散射截面σ在光電子動能為8 eV 附近出現了顯著增大,符合形狀共振在共振能量處的特征.對于單個分波的通道,l=3(f)分波在形狀共振能量處有顯著的散射截面增強效應,且與所有分波的散射截面隨能量的變化趨勢相似、增幅相當,而其他分波通道在共振能量附近只出現了輕微的調制,均沒有出現明顯散射截面的增強效應.因此,可推斷f分波通道對形狀共振過程起最顯著的作用.

4 結論

本文在實驗上利用了基于高次諧波阿秒脈沖串及反沖動量譜儀構建的阿秒符合干涉儀,對NO 分子的 4σ形狀共振過程進行了電子離子三維動量符合測量,利用RABBIT 方法獲得NO 分子的光電子譜進行擬合與相位提取,得到形狀共振過程中有效光電離延時隨光子能量的變化關系,發現實驗探測到的雙光子電離延時與單光子電離延時的變化密切相關,同時該形狀共振過程中電離延時整體特征主要由單光子電離延時決定.本文測量了關于NO 分子形狀共振中光電離延時的能量依賴關系,以及單光子電離延時與雙光子電離延時對比,對于探究分子阿秒時間尺度電子超快動力學行為以及連續態電子共振具有重要意義.