分數階憶阻耦合異質神經元的多穩態及硬件實現

丁大為 盧小齊 胡永兵 楊宗立 王威 張紅偉

(安徽大學電子信息工程學院,合肥 230601)

不同的神經元之間具有異質性,神經元活動具有很大的差異,因此研究異質神經元之間的耦合越來越受到關注.本文將Hindmarsh-Rose 神經元模型和Hopfield 神經元模型經過憶阻電磁感應耦合,構成一個新的神經元模型.利用相圖、分岔圖、李雅普諾夫指數圖和吸引盆,證明對于耦合強度和其他參數,新的神經元模型表現出不同吸引子共存現象.在保持相關參數不變時,通過改變初始狀態,可以觀察到系統的多穩態現象,包括不同周期的共存,周期與混沌現象的共存等.最后基于高級RISC 機 (advanced RISC machine,ARM)的微控制單元 (micro control unit,MCU)實現了該神經元模型,實驗結果表明理論分析的有效性.

1 引言

憶阻器是一種電阻或電導隨時間變化的電路元件,其描述了電荷和磁通量之間的關系,此外,磁控憶阻和荷控憶阻是憶阻器的主要表現形式[1].憶阻器由于可塑性和非易失記憶的特性,成為除了電阻、電感、電容以外的第4 個基本電路元件[2].當憶阻器涉及神經元回路時,各種憶阻器可用來模擬生物神經突觸[3],作為耦合突觸表征兩個神經元膜電位之間的電位差產生的感應電流[4].

神經元是組成神經系統的基本單位[5],神經元的放電活動在信息處理和用驚人算法開發人工智能[6,7]中起著重要作用.到目前為止,已經構建了從Hodgkin-Huxley(HH)模型[8]導出的各種簡化神經元模型,如Morris-Lecar(ML)[9]、Hopfield 神經網絡(HNN)[10]、二維和三維Hindmarsh-Rose.如今,單個神經元模型自耦合或多個相同神經元之間的耦合已經有很多報道,Bao 等[11]在報道了2D HR 神經元模型的基礎上,提出的憶阻器耦合HR 神經元模型表現出豐富的動力學現象.

事實上,不同的神經元由于具有異質性,神經元活動也有很大差別[12,13].Wang 等[14]討論了耦合異質神經元中的隨機共振現象,發現在適當的異質神經元耦合情況下,系統中會發生多個隨機共振.Han 等[15]研究了改進的Hodgkin-Huxley 神經元與伴有突觸延遲的異質神經元在各種條件下的同步.此外,Cheng 等[16]發現,在耦合的異質混沌Rulkov 神經元中,改變第2 個神經元參數會影響第1 個神經元的放電模式.因此,研究異質神經元之間的耦合情況對于更準確地模擬人類神經元具有重要意義[17].不幸的是,在許多關于憶阻耦合神經元的研究中,研究者都考慮了相鄰兩個相同神經元的研究,而忽略了異質神經元的研究[18,19].

近年來,共存行為[20,21]已經成為一個非常重要的研究課題并受到廣泛關注.共存行為是一種復雜的動力學現象,包括不同周期之間的共存、周期與混沌的共存、混沌與混沌的共存,其中周期現象反應生物神經元疾病,不同的周期對應不同的神經元疾病,混沌現象反應生物正常的神經元活動,不同周期的共存、周期與混沌現象的共存等現象可能是因為神經元受到神經調節劑的調節,表現出不同的神經元活動.在同一非線性系統中,不同初始狀態下包含不同種類的穩定動力學行為[22].特別在不同初始條件下,包含3 個或更多不同狀態的吸引子共存,被稱為多穩態[23].多穩態意味著非線性系統中存在著豐富多樣的穩定狀態,這反映了大腦本身的特征,大量的電生理學實驗表明,在生物神經元的電活動中存在多穩態的放電模式[24,25],這種多穩態行為可能是神經元受到神經調節劑的調節,這對研究神經元的動態記憶和信息處理有很多潛在的影響.從動力學角度揭示不同類型的多穩態有助于深入理解多穩態在大腦信息處理和認知功能中的作用.

在上述工作的基礎上,本文提出了一種新的分數階憶阻耦合異質神經元模型.選擇一個Hindmarsh-Rose 神經元模型和一個Hopfield 神經元模型,兩個神經元模型有很大差異.將所提出的分數階正弦憶阻器和分數階雙曲型憶阻器模擬神經突觸引入到兩個異質神經元模型中,不僅考慮兩個神經元之間的耦合情況,也考慮到單個神經元的自耦合情況,建立了五維分數階憶阻耦合異質神經元模型,新的神經元模型可以表現出豐富的動力學現象.利用相圖、分岔圖、李雅普諾夫指數圖和吸引盆,證明了對于耦合強度和其他參數,該神經元模型表現出不同吸引子共存現象.另一方面,在保持相關參數不變時,通過改變初始狀態,可以觀察到系統的多穩態現象,包括不同周期的共存,周期與混沌現象的共存等.最后通過 STM32 F750 實現了該電路,結果說明了理論分析的有效性.

2 分數階憶阻耦合異質神經元模型

2.1 分數階定義

卡普托導數是求解分數階微分方程[26]的常用方法之一,其D定義為

2.2 分數階憶阻器

隨著憶阻器的發展,憶阻器的模型表達式越來越豐富,根據卡普托定義,具有正弦憶導函數的分數階憶阻器的數學形式為

其中v和i是憶阻器的輸入、輸出端口,ψ為內部變量,k1和k2為電磁感應強度,分數階q滿足 0＜q＜1.憶導函數Wq(ψ)表示為

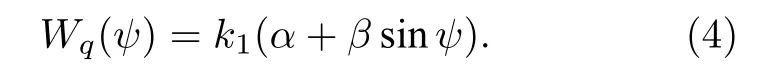
當分數階q=0.95 時,在保持參數α=1,β=1.25 的條件下,研究了在不同信號頻率和信號幅度下,憶阻器的動力學行為.當選擇幅度為A、頻率為F的正弦電壓信V=Asin(2πFt)作為驅動源時,在頻率F=1 和初始狀態x(0)=1,用振幅A的不同值;以及振幅A=4 和初始狀態x(0)=1 用頻率F的不同值固定時,憶阻器相關的收縮磁滯回線分別如圖1(a),(b)所示.當具有不同幅度和頻率的正弦信號驅動時,6 個收縮磁滯回線穿過電壓-電流平面中的原點.在圖1(b)中,隨著激勵頻率從0.4 kHz 增大到3 kHz,滯后波瓣面積逐漸減小.很明顯,當頻率增大到無窮大時,收縮磁滯回線將趨向于單值函數.顯然,所提出的數學模型表現出憶阻器的特性.

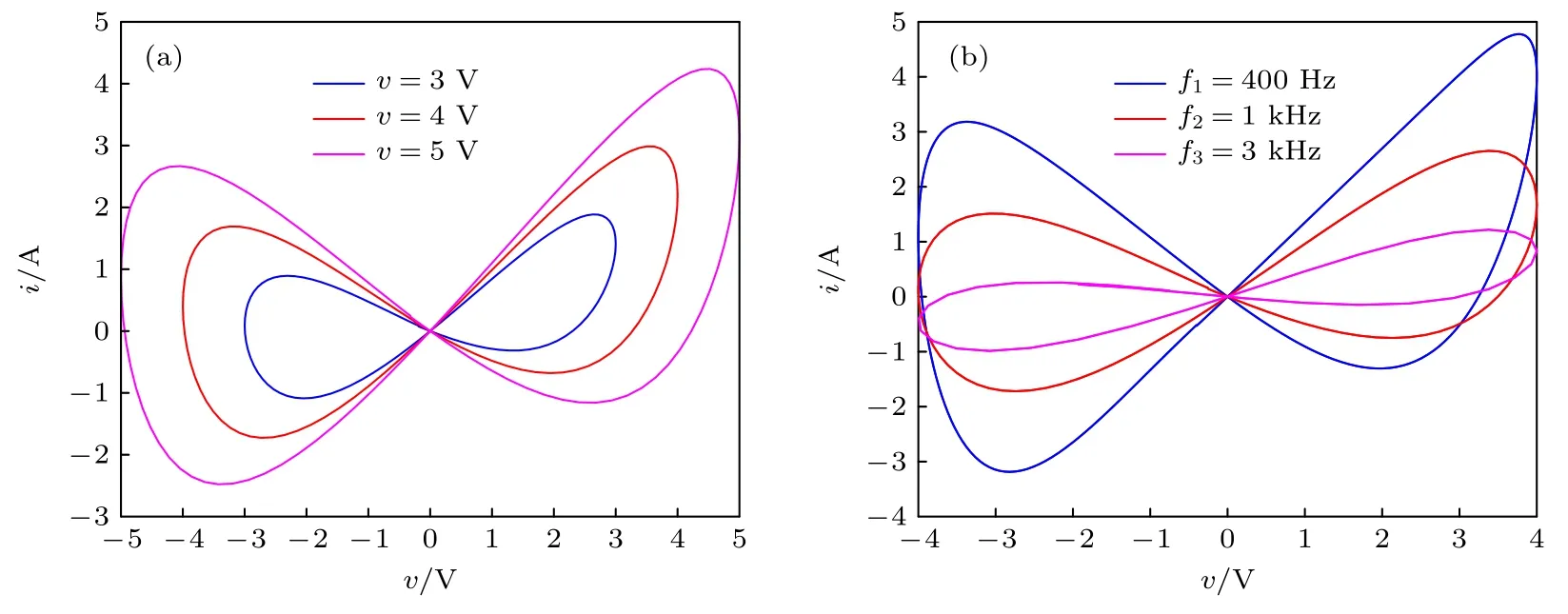
圖1 分數階憶阻器的磁滯回線 (a)F=1,不同的振幅;(b)A=4,不同頻率Fig.1.Hysteresis loop of fractional-order memristor: (a) Different amplitudes for F=1;(b) different frequencies for A=4.

2.3 分數階憶阻耦合異質神經元模型

由于不同神經元之間的異質性,異質神經元耦合的動力學現象更是豐富多彩.如今,對異質神經元之間的耦合研究的內容還很少,為此將兩個不同的分數階神經元模型經過憶阻電磁感應耦合構成一個新的神經元模型,拓撲結構如圖2 所示,新的耦合神經元模型如下:

圖2 耦合神經元的拓撲結構Fig.2.Topology of coupled neurons.

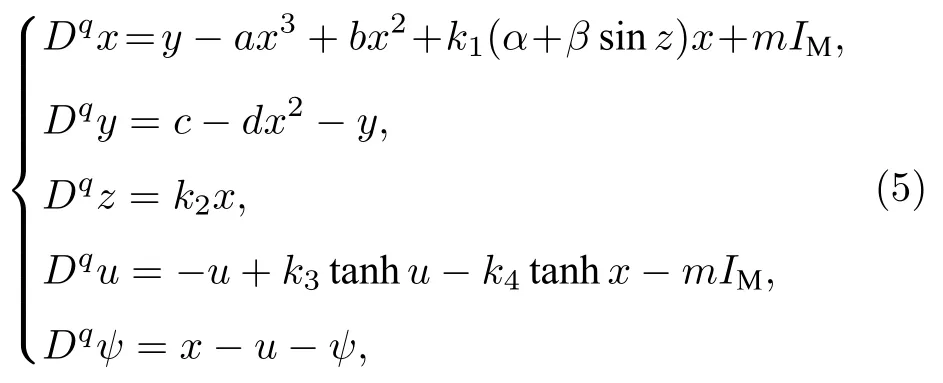
其中x表示Hindmarsh-Rosesh 神經元膜電位,y表示Hindmarsh-Rosesh 神經元的恢復變量,u表示Hopfield 神經元的狀態向量.z和ψ表示憶阻器內部狀態函數.a,b,c,d,k3,k4為系統參數,α,β,k2為憶阻參數,設定系統參數和憶阻參數為a=1,b=3,c=1,d=5,α=0.1,β=1.25,k2=0.35,k3=3.8,k4=1.9,k1為Hindmarsh-Rose神經元的自耦合系數,m為異質神經元之間的憶阻電磁感應耦合系數,電磁感應電流IM由兩個相鄰神經元之間的膜電位差感應的,可以通過非理想磁通控制憶阻器來表征,分數階閾值憶阻器產生的感應電流IM表示為

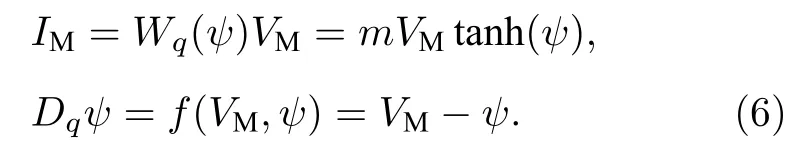
2.4 分數階憶阻耦合異質神經元平衡點分析

模型(5)的平衡點可以由下式得到:

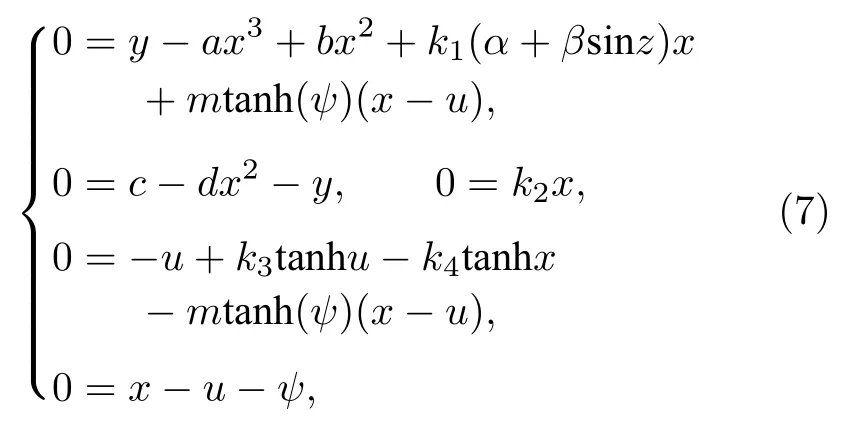
該耦合神經元的平衡點E為

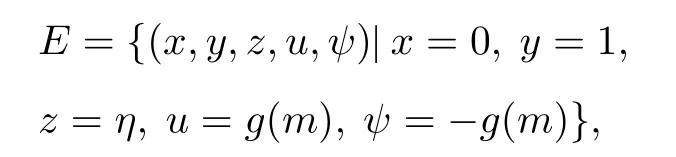
式中η為任意常數,g(m)為確切的常數,由于線平衡點的關系,該耦合神經元模型有無數個平衡點.該耦合神經元模型在平衡點E的雅可比矩陣J為

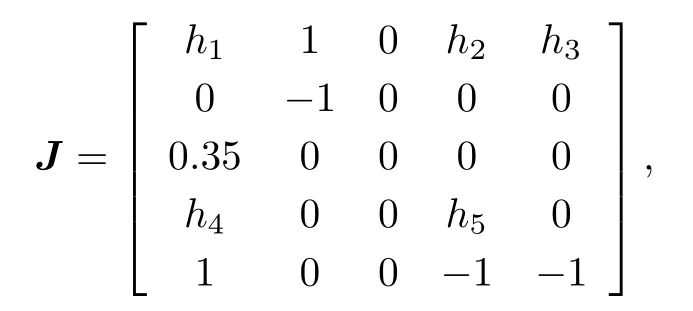
其中,h1=k1(0.1+1.25 sinη)+mtanh(-g(m)),h2=-mtanh(-g(m)),h3=-mg(m)[1-tanh2(-g(m)],h4=-1.9-mtanh(-g(m)),h5=-1+3.8[1-tanh2(g(m))]+mtanh(-g(m)).因此,系統平衡點的特征值是下列方程的解:

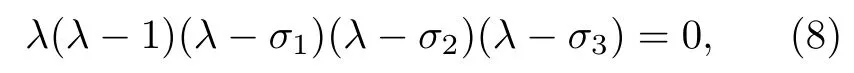
式中,σ1,σ2,σ3是關于參數m的函數,且都為實數.該耦合神經元模型的五個特征值如下:

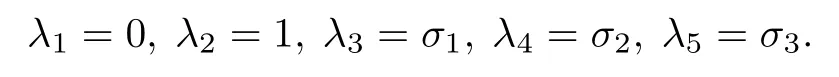
當σ1,σ2與σ3取不同的值時,系統平衡點E的特征值情況如表1 所列.

根據Routh-Hurwrite 定理,在平衡點處的雅可比矩陣具有正實根,因此,該系統的平衡點全為不穩定平衡點,該耦合神經元模型是不穩定系統.

3 初始狀態不同的共存分岔現象

分數階憶阻耦合異質神經元模型表現出顯著的多穩態現象.當系統參數固定時,在不同初始條件下,該分數階憶阻耦合異質神經元模型包含3 種不同狀態的吸引子共存,通過分叉圖,以及對應的相圖可以清晰地觀察到多穩態現象的存在.

3.1 分數階憶阻耦合神經元模型隨耦合系數 m 變化的共存分岔

當參數k1=1.25 時,選擇初始值(0 0 0 0–3),(0 0 3 1–3)和(0 0 3 0–3),分數階憶阻電磁感應耦合異質神經元模型m的共存分岔和前兩個Lyapunov 指數如圖3 所示.圖3(a)中,紅色軌跡為初始值(0 0 0 0–3)的分叉圖,藍色軌跡為初始值(0 0 3 1–3)的分叉圖,洋紅色軌跡為初始值(0 0 3 0–3)的分叉圖.每個初始值對應的前兩個 Lyapunov指數位于圖3(b).

圖3(a)中不同初始值的分叉圖表明神經元模型的共存現象,當初始條件為(0 0 0 0–3)時,系統(5)式從混沌現象開始過渡周期4,在經過兩次反向倍分岔行為過渡到周期二和周期一放電,初始條件為(0 0 3 1–3)時,系統(5)式從周期一過渡到混沌區域然后進入周期四放電,同樣在經過兩次反向倍分岔行為到周期二和周期一放電,而當初始條件為(0 0 3 0–3)時發現系統大部分區域內處于周期一放電,只有在特定的區域內發生跳躍,變為周期二放電.與之對應得前兩個 L yapunov 指數經過對比發現與分叉圖吻合.

圖3 關于耦合系數m 的共存現象 (a)關于m 的分岔圖;(b)對應前兩個 L yapunov 指數圖Fig.3.Coexistence of coupling coefficients: (a) Bifurcation diagram of the relationship;(b) corresponding to the first two exponential diagrams.

給定一些確定值m,在x-y平面上系統(5)的吸引子多穩態現象如圖4 所示,其中藍色、紅色和洋紅色軌道的初始值分別表示(0 0 3 1–3),(0 0 0 0–3)和(0 0 3 0–3).同時,在圖4 中可以發現,不同周期吸引子和混沌吸引子的共存以及不同周期吸引子的共存.特別地,不同拓撲結構的周期性吸引子和不同拓撲結構的混沌吸引子都出現在分數階憶阻器耦合的異質神經元中.

圖4 確定值 m,x-y 平面上的相圖 (a)m=0.015 ;(b)m=0.05;(c)m=0.215;(d) m=0.26Fig.4.Determination of values,phase diagrams on the x-y plane: (a)m=0.015;(b) m=0.05;(c) m=0.215;(d) m=0.2.

3.2 局部吸引子盆地

對于不同吸引子狀態共存現象,圖5 給出了分數階憶阻耦合異質神經元的吸引子共存的吸引子盆地.當耦合強度m=0.22 時,給定不同k1的值,在 (x(0)y(0)ψ(0))=(10-5)時,給出了z(0)-u(0)初始平面的局部吸引盆如圖5(a),(b)所示.當k1=1.5 時,可以清晰觀察到黃色和青色兩種顏色的共存見圖5(a),其中黃色代表周期二,青色代表周期一.當k1=1.8 時,可觀察到綠色、黃色、青色3 種顏色的共存見圖5(b),其中綠色代表混沌狀態,黃色代表周期四,青色代表周期一.通過比較圖5(a),(b),當k1取不同值時,會改變分數階憶阻耦合異質神經元的吸引子共存現象.

圖5 k1 取不同值時 z(0)-u(0)初始平面的局部吸引盆 (a)k1=1.5;(b) k1=1.8Fig.5.Local attraction basin of the z(0)-u(0) initial plane with different values: (a) k1=1.5;(b) k1=1.8.

當k1取不同值時,分數階憶阻耦合異質神經元的吸引子共存現象有較大差異,當初值不同時可以由y-u平面的相圖觀察到不同狀態的吸引子共存現象如圖6 所示.當k1=1.5 時,選取初值(1 0 1.5 0–5)以及(1 0 0 0–5)繪制y-u平面相圖,可以觀察到周期一的吸引子與周期二吸引子共存.當k1=1.8 時,選取初值(1 0 1 0.6–5),(1 0 1.5 0–5)及(1 0–1 0–5)繪制y-u平面相圖,可以觀察到周期一吸引子、周期四吸引子以及混沌吸引子共存.

圖6 k1 取不同值時,y-u 平面的吸引子共存現象 (a)k1=1.5;(b) k1=1.8Fig.6.Coexistence of y-u plane attractors with different values: (a) k1=1.5;(b) k1=1.8.

4 憶阻耦合異質神經元模型的硬件實現

混沌系統的硬件實現是驗證該混沌系統可行性的重要方法之一.由于單片機使用廣泛且價格實惠,因此,本文使用STM32 F750 系列開發板對該混沌系統進行硬件實現.該實驗平臺使用一個雙蹤模擬示波器(GW INSTEK GOS-6021)捕獲單片機(STM32 H750/F750)所產生的模擬序列,最終在模擬示波器上顯示該序列.

圖7(a)顯示了程序流程圖.STM32 系統初始化后,設置系統的各種參數及初始值,然后開始迭代計算.將結果推入堆棧中,以便于下一次計算以調用結果.數據處理后的結果通過數據輸出.在實驗中,我們設置了與文章中所出現的參數以及初始值,STM32 實現硬件連接圖如圖7(b)所示,調試完成后,得到了系統的實驗相圖如圖8.比較圖8中MATLAB 數值仿真相圖與單片機實驗結果,可以得出結論,已經成功地完成了該混沌系統的單片機硬件實現.

圖7 (a) STM32 實現的編程流程;(b) STM32 實現的實驗平臺Fig.7.(a) STM32 realized programming flow;(b) STM32 realized experimental platform.

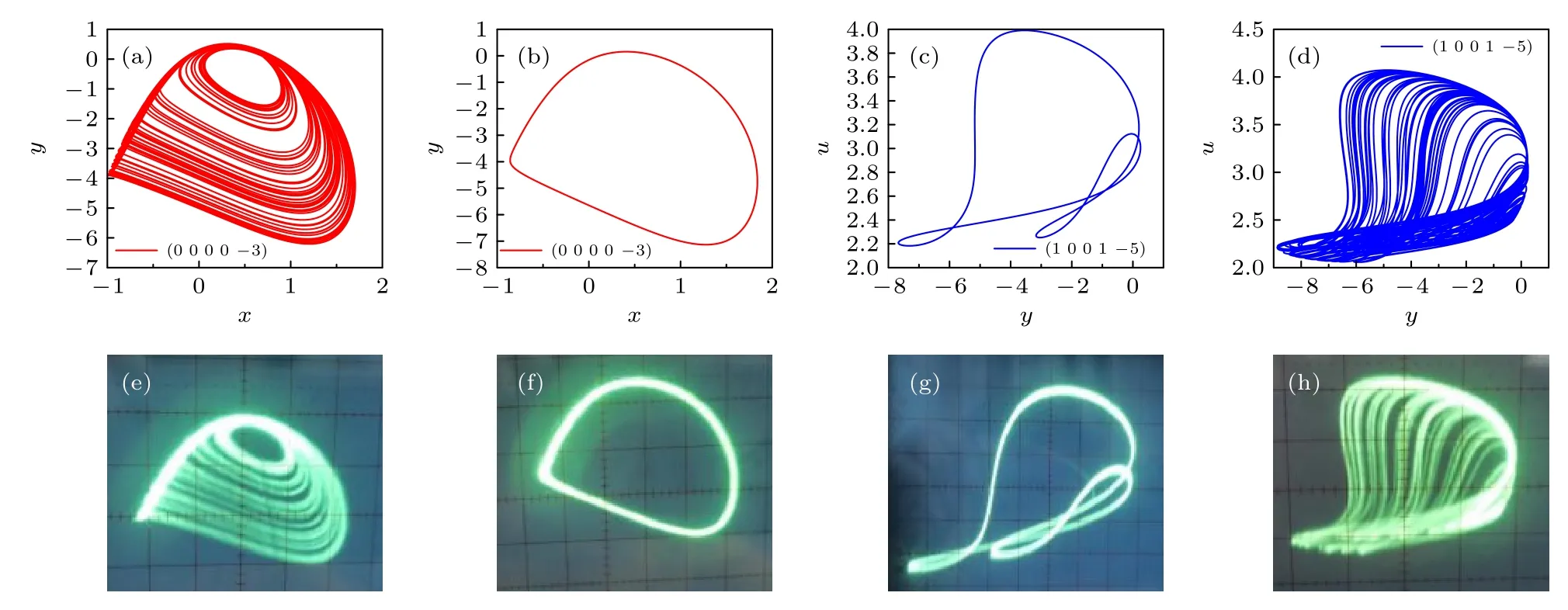
圖8 部分參數的 MATLAB 仿真圖和單片機實驗結果 (a)—(d) MATLAB 仿真圖;(e)—(h)單片機實驗結果Fig.8.Simulation diagram of some parameters and experimental results of MCU microcomputer: (a)–(d) Simulation diagram;(e)–(h) experimental results of single-chip microcomputer.

5 結論

本文研究了分數階電磁感應耦合異質神經元的多穩態現象,將一個Hindmarsh-Rose 神經元模型和一個Hopfield 神經元模型經過憶阻感應耦合建立一個新的神經元模型.在給定不同的初始條件時,憶阻電磁感應耦合神經元模型可以觀察到多穩態現象.利用相圖、分岔圖、李雅普諾夫指數圖和吸引盆,證明了對于耦合強度和其他參數,新的神經元模型表現出多穩態現象,經過MATLAB 數值模擬驗證了結果.最后,通過單片機實驗平臺對本文部分相圖進行實現,得到的實驗結果與數值模擬結果一致.