利用雙慢變量的快慢變量分離分析新腦皮層神經元Wilson 模型的復雜電活動*

梁艷美 陸博? 古華光

1) (河南科技學院數學科學學院,新鄉 453003)

2) (同濟大學航空航天與力學學院,上海 200092)

具有重要、廣譜的生理功能的大腦新皮層神經元表現出規則和快速峰放電、內源性和連續型簇放電,受到兩個慢變量 (T 型鈣和鈣激活的鉀離子通道) 的調控 (Wilson 模型).若只選取更慢的慢變量進行單慢變量的快慢變量分離,不能獲得Wilson 模型的簇放電的動力學機制,因為此時的快子系統還含有另一個慢變量.因此,本文采用雙慢變量的快慢變量分離方法進行分析.首先獲得快子系統在參數平面上的分岔及分岔曲線與簇放電相軌線的交點;基于兩個慢變量都不足夠慢導致的只有部分交點對應的分岔與簇放電相關,本文進一步獲得三維空間中分岔曲線與相軌跡的位置關系,識別出與簇放電相關的分岔,并排除無關的分岔.結果發現,內源性簇放電與不變環上的鞍結分岔有關、與鞍結分岔無關,連續型簇放電與不變環上的鞍結分岔和超臨界霍普夫分岔有關、與鞍結分岔無關.本研究全面深入認識了新腦皮層神經元簇放電的動力學機制,為調控放電模式奠定了基礎.

1 引言

神經元是神經系統的基本結構單位,通過電活動實現各種生理功能.神經元電活動主要包括峰放電 (spiking) 模式、簇放電 (bursting) 模式及靜息(resting state) 等[1],在感覺、認知、運動控制和疾病等方面發揮著重要作用[2?5].峰放電模式表現出連續快速放電,而簇放電模式表現為簇 (burst,連續快速的放電峰(spike)) 與休止期的交替.揭示放電模式隨參數變化的轉遷規律或分岔序列有助于認識神經系統的功能.例如,溫度和鈣離子誘發神經元電活動從簇放電到峰放電的轉遷規律,分別與溫度和痛覺相關[6,7];鉀離子濃度調控峰放電到簇放電 (擴散性抑制) 的轉遷與偏頭疼相關[8].除了放電模式隨參數的轉遷規律,放電模式產生的內在動力學及在外界調控下的復雜動力學也是神經動力學的重要環節.

簇放電模式的產生與慢變量調控有關,快慢變量分離結合分岔已經被廣泛用于揭示簇放電的內在機制[9?12].神經元系統可以分解為快子系統和慢變量,如Hindmarsh-Rose 模型和Chay 模型,是由二維快子系統和一個慢變量構成的.這些模型的簇放電的動力學機制已經獲得較為全面和深入的理論認識.快子系統會表現出峰放電、靜息以及峰放電與靜息之間的分岔;慢變量調控下簇放電行為會在快子系統的峰放電和靜息之間轉遷,簇的起始和結束對應于快子系統的分岔[9].因此,不同的簇放電模式就是由簇的起始和結束的分岔不同所決定的.快慢變量分離已經廣泛用于揭示不同調控下的簇放電的復雜動力學機制,如pre-B?tzinger 復合體 (pre-B?tzinger complex) 的簇放電[12?14].此外,具有時滯的突觸流與噪聲可以作用到快子系統的分岔點附近通過改變運行軌跡來引起新的節律[15?20],而不具有時滯的多類調控可以通過改變快子系統分岔引起復雜的節律[21,22].這些復雜的放電節律還對興奮性作用引起放電增強或抑制性作用引起放電降低的傳統觀念提出了挑戰,豐富了非線性動力學的內涵[23?26].

雖然快慢變量分離能成功用于揭示只有單個慢變量的簇放電的動力學,但是,當慢變量不足夠慢時,簇的起始和結束相位與快子系統分岔點的位置關系會有些偏差[27].更為重要的是,在實際的神經系統中,往往會受到兩個及兩個以上的慢變量的調控.例如,胰腺β細胞受到兩個慢速鉀電流的調控[28],偏頭疼出現時的海馬錐體神經元受到鉀和鈉離子濃度兩個慢變量的調控[29],損傷神經纖維受到細胞內和內質網的鈣離子濃度兩個慢變量的調控[30].此外,還有描述新腦皮層神經元電活動的理論模型 (本文稱為Wilson 模型[31]),受到低閾值T 型鈣流和鈣激活的鉀離子超極化電流的調控等.如何對多個慢變量調控的簇放電進行快慢變量分離獲得其內在動力學機制仍是有待解決的重要問題.最近,已有研究關注了兩種雙慢變量調控的簇放電動力學.一種是以胰腺β細胞[28]的簇放電為代表,兩個慢變量中的一個比另一個慢很多,此時,將更慢的慢變量看作常數來簡化模型,再進行單慢變量的快慢變量分離.另一種是以海馬錐體神經元中的簇放電為代表,兩個慢變量 (鉀和鈉離子濃度) 都特別慢.若只選擇其中一個慢變量進行快慢變量分離,快子系統的分岔不能與簇的起始和結束相匹配,說明單慢變量的快慢變量分離對于分析具有雙慢變量的簇放電已經失效[29].因此,文獻[29]將兩個慢變量同時看作分岔參數,對快子系統進行雙參數分岔分析,獲得了多類余維–1 分岔曲線,簇放電的相軌跡與余維–1 分岔曲線的交點對應著簇的起始和結束.實際上,受兩個慢變量調控的簇放電還有很多不同的情形,例如,描述新腦皮層神經元放電的理論模型—Wilson 模型的兩個慢變量都不足夠慢,與上述兩種都不同,可能需要提出新的雙慢變量的快慢變量分離的流程.

哺乳動物新腦皮層在神經系統高級功能的實現中起著廣泛和重要的作用.在新腦皮層神經元觀察到4 類基本的放電形式[32?35]: 規則峰放電 (regular spiking,RS)、快速峰放電 (fast spiking,FS)、連續型簇放電 (continuous bursting,CB) 和內源性簇放電 (intrinsic bursting,IB),涉及多類離子電流[36],例如鈉流、鉀流、T 型鈣流 (IT) 和鈣激活的鉀離子超極化電流(IAHP).RS 神經元主要是第4 層的棘星細胞 (spiny stellate cells) 和第2,3,5 和6 層的錐體神經元,起興奮性調控作用.FS 神經元是非錐體細胞,例如,γ氨基丁酸能中間神經元 (GABAergic interneurons)[37],與感覺及皮層節律有關.FS 表現出后超極化 (after-hyperpolarization,AHP) 和高頻特性,是因為鉀流在復極化和AHP 中起重要作用[38].CB 神經元主要是棘星細胞和第2,3,4 層的錐體神經元,產生具有高頻峰的簇放電,簇內峰的幅值明顯降低,簇通過后去極化 (after-depolarization,ADP) 結束[39].視覺誘發的GAMMA 振蕩與CB 神經元的同步活動相關[40].IB 神經元在強直流作用下生成簇放電,然后在電流的作用下表現為伴隨ADP 的低頻峰放電.IB 神經元對應興奮性錐體神經元,特別是在第5 層最為豐富.例如,IB 簇放電與癲癇[41]或慢波睡眠[42]有關.因此,了解皮層神經元的不同電活動對于了解大腦皮層的正常功能和病理生理過程至關重要.

理論上,基于主要的離子流INa,IK,IT和IAHP的新皮層神經元模型 (wilson model)[31]被提出,可以模擬FS,RS,IB 和CB 四種放電形式.已有諸多關于該模型的網絡動力學和單神經元放電的動力學的研究.例如,利用RS 或IB 神經元網絡研究動作電位波形依賴于慢電導刺激[43]、多巴胺影響GAMMA 同步振蕩與注意力的關系[44],以及小世界耦合的RS 和IB 神經元網絡的同步振蕩機制[45].在單神經元中,研究了不同調控下的Wilson 模型的動力學行為.例如,只調控直流激勵或同時調控IT和IAHP,誘發FS,RS,Bursting 和混沌等不同放電模式之間的躍遷,表明混沌可以通過加周期或倍周期分岔產生[46].但是,由于該模型為四維模型,含有兩個快變量和兩個慢變量,比一般的三維 (兩個快變量和一個慢變量) 的描述簇放電的動力學模型復雜.因此,到目前還沒有對四維Wilson 模型的4 類放電特別是簇放電的內在動力學的認識.該模型的復雜特性對于放電動力學分析,特別是簇放電的分析帶來了困難,因此有許多研究對Wilson模型進行簡化,簡化為兩維或三維模型,并用于研究皮層神經元的電活動[47?52].但是,二維Wilson模型需要其他調控才能產生簇放電.到目前為止,對于Wilson 模型的復雜放電特別是簇放電的內在動力學 (與快子系統的分岔的關系) 還沒有全面和深入研究,對于外界調控下的放電模式的諸多研究也未與內在動力學建立聯系,這是亟待解決的問題.

本文提出了適合于分析Wilson 模型簇放電的雙慢變量的快慢變量分離流程,利用單和雙慢變量的快慢變量分離來研究四維Wilson 模型峰放電和簇放電產生的動力學機制.首先,仿真了4 類放電及放電模式隨參數的變化規律.其次,利用單參數的快慢變量分離揭示了兩類峰放電的動力學機制.再次,發現單慢變量的快慢變量分離不能有效分析兩類簇放電,簇的開始或結束相位與快速子系統的分岔點不匹配,簇內峰的幅值與極限環的幅值也不匹配.這是因為快子系統含有另一個慢變量不能作為快子系統而導致.為了克服這個問題,提出了新的雙慢變量的快慢變量分離的操作流程.將慢變量T和H都作為快子系統的分岔參數,在 (H,T)空間得到余維–2 分岔點 (Bogdanov-Takens (BT)分岔和Cusp 分岔) 和多個余維–1 分岔曲線,包括不變環上的鞍結分岔 (saddle-node on invariant circle bifurcation,SNIC)、亞臨界霍普夫分岔 (subcritical Andronov-Hopf bifurcation,SubHopf)、超臨界霍普夫分岔 (supercritical Andronov-Hopf bifurcation,SupHopf) 和鞍-同宿軌分岔 (saddle-Homoclinic orbit bifurcation,SHC).然后,在獲得簇放電的相軌跡與余維–1 分岔曲線在 (H,T) 平面上的交點的基礎上,進一步得到它們在 (H,T,V) 三維空間中的位置關系,識別了交點中與簇的起始和結束的局部動力學相關的分岔,并排除了無關的分岔,獲得了簇內峰的幅值與穩定極限環幅值的關系.本研究與兩個慢變量都很慢的錐體神經元的結果[29]有兩處不同,一是簇放電的軌線與分岔點的位置有些許偏差,這由慢變量不夠慢導致;二是要在 (H,T,V) 三維空間中進一步識別簇放電相軌跡和分岔的位置關系,識別出與簇放電相關的分岔并排除無關的分岔,給出了一類適用于分析兩個慢變量不是很慢的簇放電的方法.本研究具有兩個方面的意義,一是給出一類新的雙慢變量的快慢變量分離的操作流程,適用于兩個慢變量都不是很慢的情形;二是深入認識新腦皮層神經元的兩類峰放電和兩類簇放電的復雜內在動力學.該研究可以為揭示不同調控下的放電模式的復雜動力學奠定基礎.

2 模型與方法

2.1 Wilson 模型

Wilson 模型是常用來描述新皮層神經元峰放電和簇放電的理論模型[31],其方程如下:

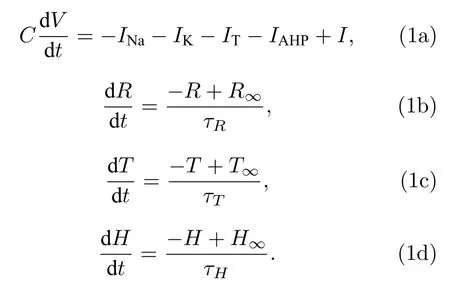
該模型有4 個變量,分別為電壓變量V,鉀通道恢復變量R,與鈣離子電流有關的電導變量T,與鈣激活的鉀離子電流有關的電導變量H.C代表神經元的電容.τR,τT和τH分別代表IK,IT和IAHP流的時間常數.I表示去極化電流.其中INa,IK,IT和IAHP分別代表鈉流、鉀流、低閾值T 型鈣流和鈣激活的鉀離子超極化電流,對應的方程分別為:INa=m∞(V-ENa),IK=gRR(V-EK),IT=gT T×(V-ECa)和IAHP=gHH(V-EK).式中gR,gT和gH分別是鉀離子、鈣離子和鈣激活的鉀離子的最大電導,ENa,EK和ECa分別是鈉離子、鉀離子和鈣離子的反轉電位,函數m∞,R∞和T∞是關于膜電位V的多項式,各項表達式為:m∞=17.8+47.6V+33.8V2,R∞=1.24+3.7V+3.2V2和T∞=8(V+0.725)2.

Wilson 模型采用的參數值為[31]:τT=14 ms,τH=45 ms,C=1 μF/cm2,gR=26 mS/cm2.ENa=0,EK=–0.95,ECa=1.2.方程計算出的膜電位、反轉電位的值乘以100 后的值的量綱對應mV,電流INa,IK,IT,IAHP和I的值除以10 后的值對應的量綱為 nA/cm2.為了描述簡便,后續本文的電壓和電流值不再給出量綱.

2.2 快慢變量分離

本文研究的Wilson 模型,τR=4.2 ms 或τR=1.5 ms,τT=14 ms,τH=45 ms .τT和τH大于τR,說明T和H是兩個慢變量;但τT和τH跟τR的差距不夠大,在一個量級,說明兩個慢變量不足夠慢 (根據經驗,時間常數差別在2 個數量級及以上往往是足夠慢).傳統的快慢變量分離只有一個慢變量.本文研究的簇放電模式受兩個慢變量影響,需要發展雙慢變量的快慢變量分離方法進行分析.方程 (1a)—(1d) 構成全系統.

2.2.1 單慢變量

對于RS,CB 和IB,因為τH=45 ms 較大,以H為慢變量,方程 (1a)—(1c) 為快子系統.對于FS,因為gH=0,所以以T為慢變量,方程 (1a)和 (1b) 為快子系統.對快子系統,獲得以單慢變量為參數的分岔圖.將全系統峰(簇)放電的相軌跡疊加到快子系統的分岔圖上,研究峰(簇)放電的起始和結束相位與分岔的關系.

2.2.2 雙慢變量

選取T和H同時為慢變量,則方程 (1a) 和(1b) 構成快子系統.T和H均作為分岔參數,在(H,T) 參數空間上得到快子系統的雙參數分岔.將全系統峰 (簇) 放電的相軌跡疊加到雙參數分岔平面上,得到相軌跡與分岔曲線的交點,交點對應的分岔就是可能的與簇放電的起始和結束相位相關的分岔.進一步,在三維空間探尋分岔與相軌線的準確位置關系,獲得與簇放電相關的分岔,排除與簇放電無關的分岔: 距離軌線近的就是與簇放電相關的分岔,距離遠的就是與簇放電無關的分岔.

2.3 計算方法

運用四階Runge-Kutta 的方法求解方程,積分步長為0.0001 ms,積分時間為20000 ms 以保證獲得穩態放電 (圖1 中的時間0 ms 對應積分時間的10000 ms).分岔計算通過XPPAUT[53]軟件獲得.

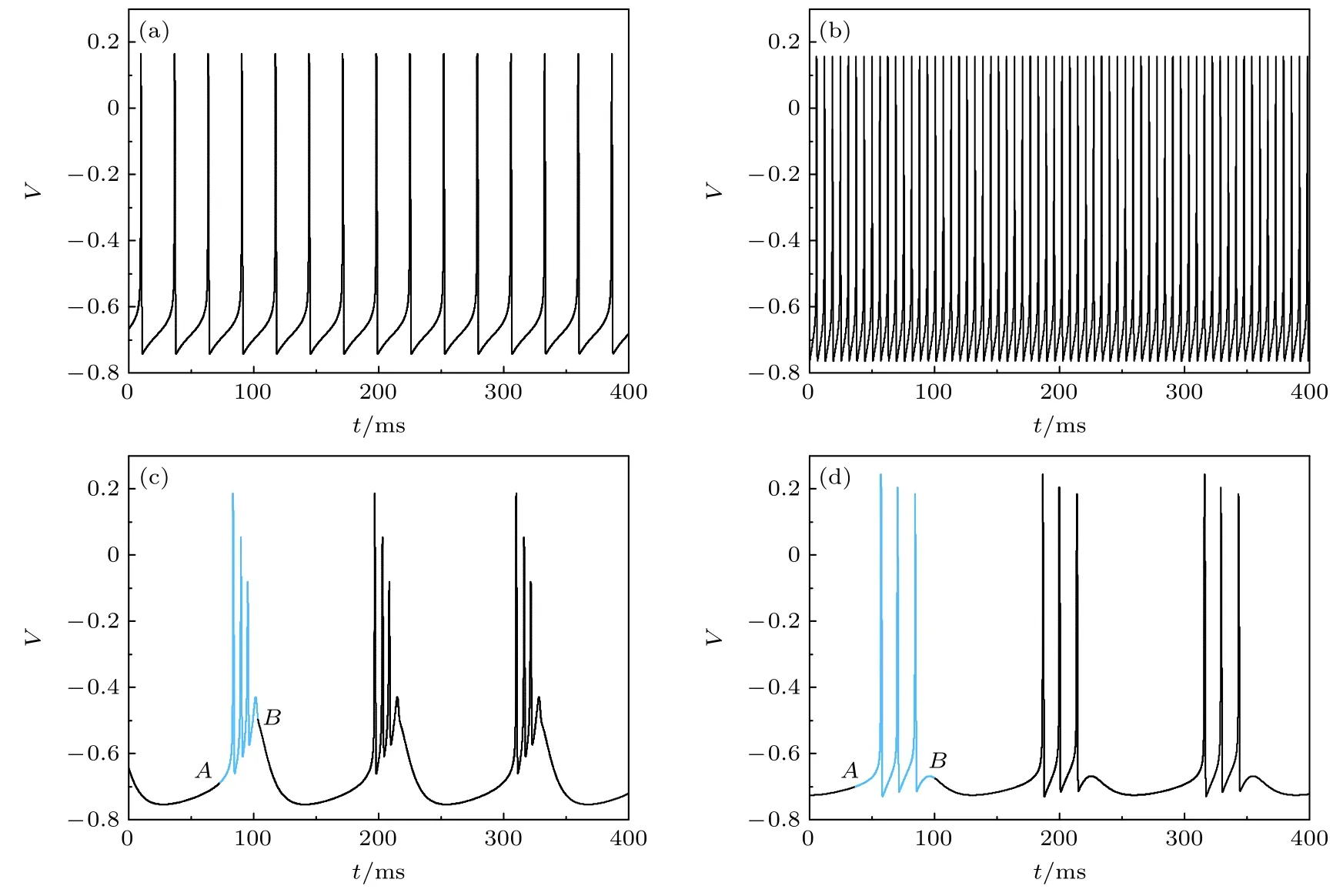
圖1 Wilson 模型在不同參數下的膜電位 (a) RS,其中 I=10,gT=0.1 mS/cm2,gH=5 mS/cm2,τR=4.2 ms;(b) FS,其中 I=3.5,gT=0.25 mS/cm2,gH=0 mS/cm2,τR=1.5 ms;(c) CB,其中 I=8.5,gT=2.25 mS/cm2,gH=9.5 mS/cm2,τR=4.2 ms;(d) IB,其中 I=3.5,gT=1.2 mS/cm2,gH=3.4 mS/cm2,τR=4.2 ms;圖 (c),(d) 中,點A 和點B 分別代表第一個簇(藍色)的起始與結束相位Fig.1.Membrane potential of Wilson model at different parameter values: (a) RS,I=10,gT=0.1 mS/cm2,gH=5 mS/cm2,τR=4.2 ms;(b) FS,I=3.5,gT=0.25 mS/cm2,gH=0 mS/cm2,τR=1.5 ms;(c) CB,I=8.5,gT=2.25 mS/cm2,gH=9.5 mS/cm2,τR=4.2 ms;(d) IB,I=3.5,gT=1.2 mS/cm2,gH=3.4 mS/cm2,τR=4.2 ms.In Fig.1 (c),(d),the points A and B represent the start and termination phases of first burst (blue),respectively.

3 結果

3.1 四類放電

通過對τR,gT,gH和I賦予不同的參數值(見圖1),模擬RS,FS,CB,IB 四種不同的電活動,膜電位的時間歷程分別如圖1(a)—(d) 所示.

RS 和FS 均表現出緊張性放電,如圖1(a),(b)所示,FS 比RS 放電頻率更高,主要是因為FS 復極化速度更快.IB 和CB 表現為周期性的簇放電模式,如圖1(c),(d)所示.正如生理學上觀察到的那樣,CB 每個簇內峰的高度依次降低,并且每個簇以去極化后電位 (ADP) 終止.

3.2 峰峰間期分岔圖

為進一步描述4 類電活動隨參數的變化,不同放電模式的峰峰間期 (inter-spike intervals,ISIs)分別隨參數I,gT和gH的變化如圖2—圖4 所示.

RS,FS,CB 和IB 電活動的ISIs 隨I變化的分岔分別如圖2(a)—(d) 所示.RS 和FS 的ISIs隨I的遞增而減小.CB 的ISIs 隨著I的變化會產生分岔.類似地,IB 的ISIs 也表現出了分岔,說明兩類簇放電在不同參數調控下會有周期數的變化.

4 類電活動的ISIs 隨gH改變的分岔如圖3(a)—(d) 所示.峰放電的ISIs 都隨gH的遞增而增長,不同的是FS 的ISIs 隨gH增大會產生倍周期分岔.CB和IB 隨gH變化表現出加周期分岔.IB 的ISIs 在gH較小時表現為周期1 的峰放電.

參數gT的改變對于神經元4 類電活動的影響如圖4(a)—(d) 所示.RS,CB 和IB 的ISIs 隨gT變化趨勢類似,該模型會經歷復雜的分岔,由峰放電轉換為不同周期數的簇放電.而FS 的ISIs 隨gT遞增逐漸減小.

圖2—圖4 展示了Wilson 模型在不同參數下展示出不同的放電模式,本文將以圖1 展示的4 類放電模式為代表進行快慢動力學分析.

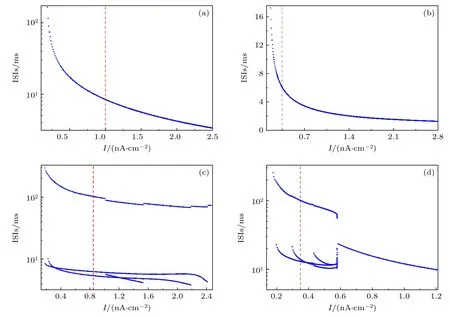
圖2 4 類放電的ISIs 關于I 的分岔 (a) RS;(b) FS;(c) CB;(d) IB.(a)—(d) 的豎虛線對應圖1(a)—(d)Fig.2.Bifurcation of ISIs with respect to I of four types of firing patterns: (a) RS;(b) FS;(c) CB;(d) IB.The vertical dotted line in panels (a)–(d) corresponds to Fig.1(a)–(d).

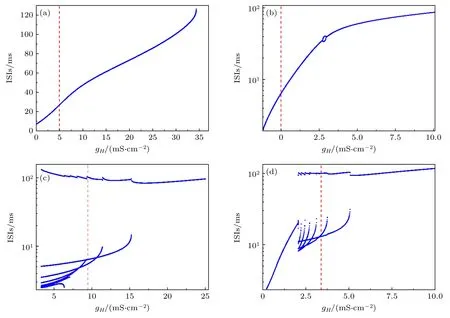
圖3 ISIs 關于 gH 的分岔 (a) RS;(b) FS;(c) CB;(d) IB.(a)—(d) 的豎虛線對應圖 1(a)—(d)Fig.3.Bifurcations of ISIs with respect to gH : (a) RS;(b) FS;(c) CB;(d) IB.The vertical dotted line in panels (a)–(d) corresponds to Fig.1(a)–(d).

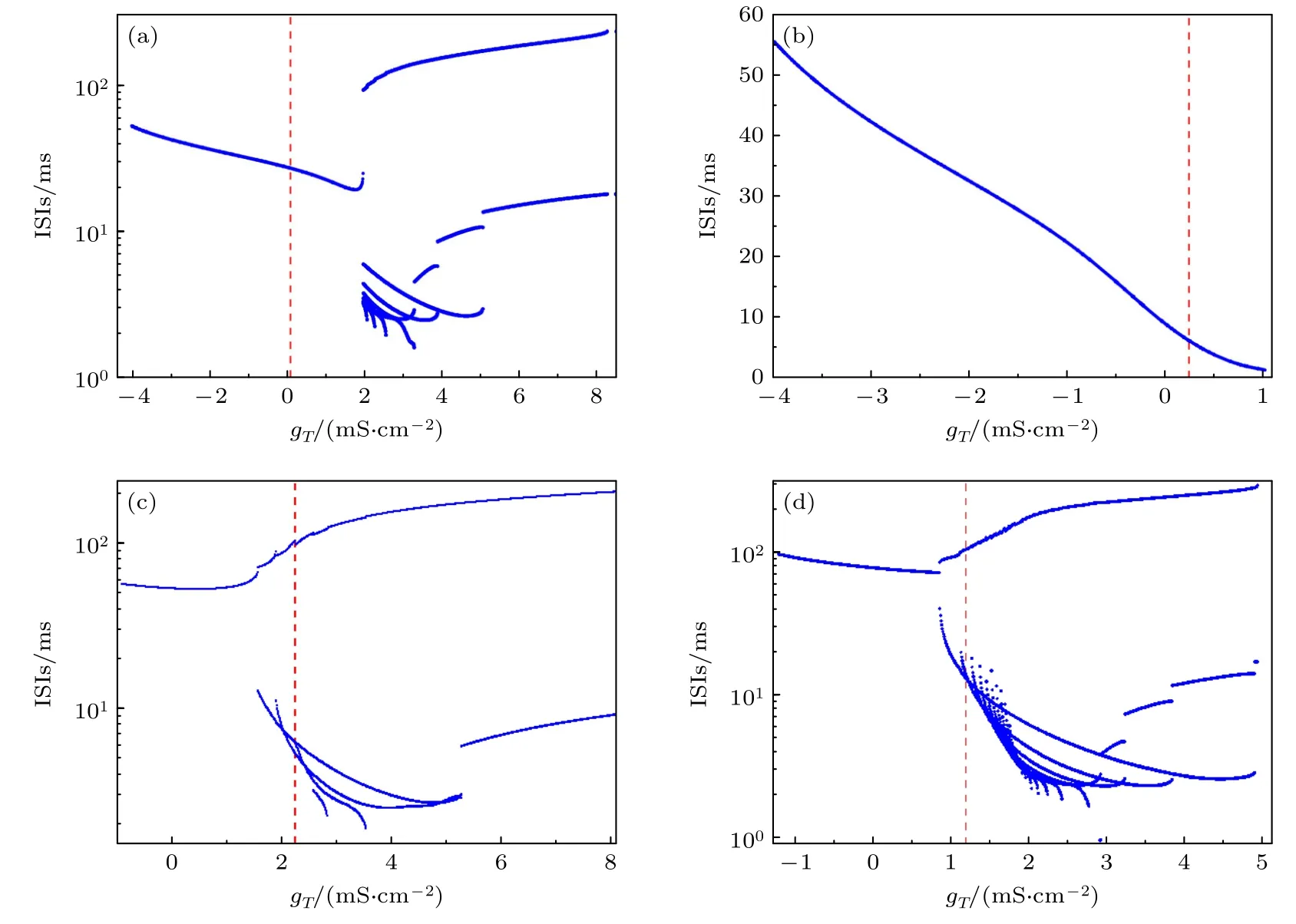
圖4 ISIs 關于 gT 的分岔 (a) RS;(b) FS;(c) CB;(d) IB.(a)—(d) 的豎虛線對應圖 1(a)—(d)Fig.4.Bifurcations of ISIs with respect to gT : (a) RS;(b) FS;(c) CB;(d) IB.The vertical dotted line in panels (a)—(d) corresponds to Fig.1(a)–(d).

3.3 峰放電和簇放電的快慢變量分離: 單慢變量

圖1(a) 的RS 的單慢變量的快慢變量分離的結果如圖5(a) 所示.快子系統的平衡點曲線呈“Z”形,由穩定平衡點 (紅色實線) 和不穩定平衡點(黑色虛線) 組成.紅色實線為穩定結點 (右下分支),具有較低膜電位,對應于靜息狀態;黑色虛線代表鞍點 (中間分支) 和不穩定焦點 (上分支).在H≈0.568757 處存在不變環上的鞍結分岔 (SNIC),穩定極限環 (最大振幅Vmax和最小振幅Vmin分別由上綠線和下綠線表示) 消失.穩定的極限環對應于放電.此外,“Z”形曲線的上拐點 (SN),出現在鞍點 (中間分支) 和不穩定焦點 (上分支) 的交點處.由圖5(a) 可以看出,快子系統極限環幅值的最大值與全系統峰放電軌線 (藍色軌跡) 幅值的極大值對應,全系統軌線都在快子系統的放電區域內,不在靜息的區域內.

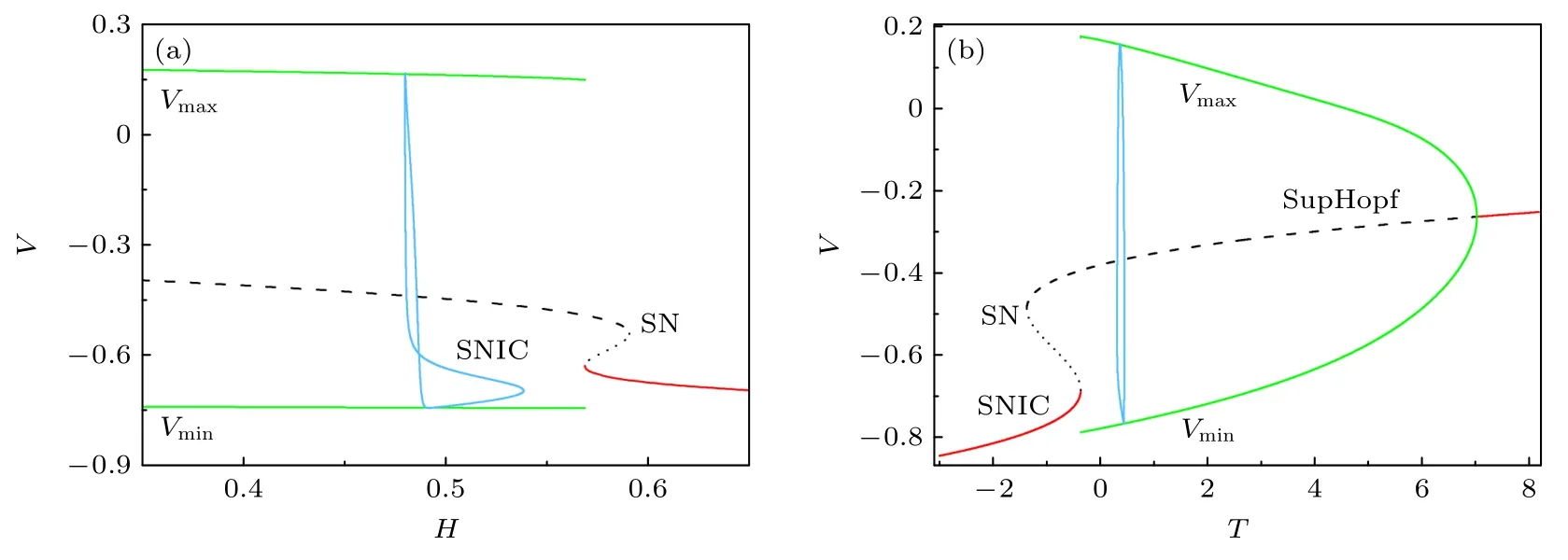
圖5 峰放電的快子系統隨H 或T 變化的分岔和峰放電的相軌跡 (藍色實線) (a) RS,SNIC 代表H≈0.568757 處不變環上的鞍結分岔;(b) FS,SNIC 和SupHopf 分別代表H≈–0.365159 處不變環上的鞍結分岔和H≈7.012722 處超臨界霍普夫分岔.紅色實線、黑色虛線分別代表穩定和不穩定平衡點.上 (Vmax) 和下 (Vmin) 綠線代表穩定極限環的最大和最小幅值Fig.5.Bifurcation of the fast subsystem of the spiking with respect to H or T and the phase trajectory of spiking (solid blue curves): (a) RS,SNIC represents saddle-node on invariant circle bifurcation at H≈0.568757;(b) FS,SNIC and SupHopf represent saddle-node on invariant circle bifurcation at H≈-0.365159 and the supercritical Andronov-Hopf bifurcation at H≈7.012722,respectively.The red solid curves and the black dashed curves represent the stable and unstable equilibrium points,respectively.Upper (Vmax) and lower (Vmin) green curves represent the maximum and minimum amplitudes of the stable limit cycle.

對于圖1(b) 的FS,gH=0,因此,將慢變量T作為分岔參數.FS 的單慢變量的快慢變量分離的結果如圖5(b) 所示.快速子系統的平衡點曲線呈“S”形,由穩定平衡點 (紅色實線) 和不穩定平衡點 (黑色虛線) 組成.左紅色實線代表穩定結點,具有較低膜電位,對應于靜息狀態;右紅色實線代表穩定焦點,具有較高膜電位,對應于去極化阻滯.黑色虛線代表鞍點 (中間分支) 和不穩定焦點 (上分支).穩定極限環 (綠色) 出現在SNIC (T≈–0.365159) 和 SupHopf (T≈7.012722) 之間,即放電區域.可以看出,FS 的相軌跡 (藍色軌跡) 的極值與極限環極值對應,位于快子系統的穩定極限環區間內.

圖1(c) 的CB 以慢變量H為分岔參數的快慢變量分離的結果如圖6(a),(b) 所示.快子系統的分岔如圖6(a) 所示,平衡點曲線呈“Z”形,上支和下支紅色實線代表穩定結點,中支黑色短劃線代表不穩定的鞍點.穩定結點與鞍點相碰形成兩個鞍結分岔點,SN1和SN2,分別位于H≈0.287483 和H≈0.718103 處.將CB 的相軌跡疊加到圖6(a)上,得到圖6(b).將CB 的相軌跡疊加到圖6(a),得到圖6(b).淺藍色和灰色實線代表CB 的簇和休止期.可以看出,簇的起始相位點A與快子系統的SN1有一定關系,休止期與快子系統的靜息有關;但是,簇的結束相位點B與快子系統的分岔無關,簇內峰的幅值與穩定極限環的幅值無關.以上結果表明,單慢變量的快慢變量分離不能解釋CB 的動力學機制,這是因為此時快子系統含有慢變量T.

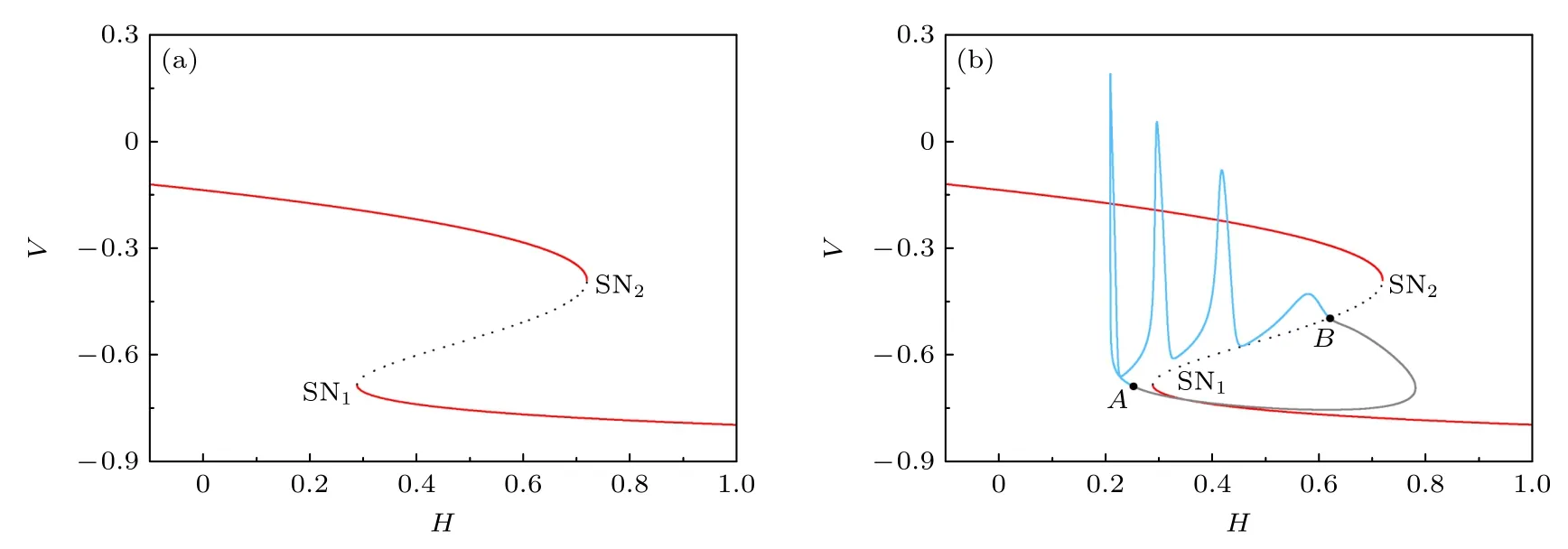
圖6 H 為慢變量時,CB 的快慢變量分離 (a) 快子系統的平衡點和極限環的分岔,在 H≈0.287483 和H≈0.718103 處的SN1 和SN2 代表鞍結分岔點,紅色實線和黑色虛線分別代表穩定和不穩定平衡點;(b) CB 相軌跡與圖 (a) 的疊加,淺藍色和灰色實線分別代表簇和休止期的相軌跡,點A 和點B 分別代表簇的起始和結束Fig.6.The fast-slow variable dissection to CB with H taken as the slow variable: (a) The bifurcations of the equilibrium point and the limit cycle of the fast subsystem.SN1 at H≈0.287483 and SN2 at H≈0.718103 represent saddle-node bifurcation points;respectively,the red solid curves and the black dashed curves represent stable and unstable equilibrium points,respectively;(b) phase trajectory of CB plotted with Fig.6(a),the light blue and gray solid curves represent the phase trajectory of the burst and the quiescent state,respectively,and points A and B represent the start and termination phases of burst,respectively.

圖1(d) 的IB 以H為慢變量的快慢變量分離如圖7(a),(b)所示.快子系統的動力學行為和分岔如圖7(a),包括靜息 (右下支紅色實線),放電(上、下綠色實線) 和去極化阻滯 (左上支紅色實線),多個平衡點的分岔 (SupHopf (H≈0.331783)和SubHopf (H≈0.919389));鞍結分岔 (SN1和SN2),極限環的鞍結分岔 (FLC1和FLC2).淺藍色和灰色實線代表簇和休止期的相軌跡,點A和點B分別代表簇的開始和結束.雖然休止期與快子系統的靜息有關,而且簇的起始相位 (點A) 比較靠近SN1分岔,結束相位 (點B) 比較靠近FLC1,但簇內峰的幅值與穩定極限環的最大、最小值 (上、下綠色實線) 并不匹配.不匹配的原因是此時系統還有慢變量T.

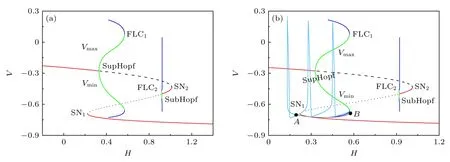
圖7 H 為慢變量時,IB 的快慢變量分離 (a) 快子系統的平衡點和極限環的分岔;(b) IB 相軌跡與圖 7 (a) 的疊加,上、下支紅色實線和中支黑色短劃線、點線分別代表穩定和不穩定平衡點.上、下綠色 (深藍色) 實線分別代表穩定 (不穩定) 極限環,淺藍色和灰色實線代表簇和休止期的相軌跡,點A 和B 分別代表簇的起始與結束.SN,SubHopf,SupHopf 和FLC 分別代表鞍結分岔、亞臨界霍普夫分岔、超臨界霍普夫分岔和極限環的鞍結分岔Fig.7.The fast-slow variable dissection to IB with H taken as the slow variable: (a) Bifurcation of the equilibrium point and limit cycle of fast subsystem;(b) phase trajectory of IB plotted with Fig.7(a).The upper and lower red solid curves represent stable equilibrium points,and the middle black dashed and dotted curves represent unstable equilibrium points,respectively.The upper and lower green (dark blue) solid curves represent the stable (unstable) limit cycles.The light blue and gray solid curves represent the phase trajectory of the burst and the quiescent state,and points A and B represent the start and termination phases of burst,respectively.SN,SubHopf,SupHopf,and FLC represent the saddle-node bifurcation,the subcritical Andronov-Hopf bifurcation,the supercritical Andronov-Hopf bifurcation,and the fold limit cycle bifurcation,respectively.

3.4 簇放電的快慢變量分離: 雙慢變量

對于CB 和IB,H和T同時作為慢變量,由變量V和R構成的方程 (1a)和(1b) 作為快子系統,快子系統中的H和T作為分岔參數.在 (H,T) 空間上獲得的快子系統的雙參數分岔結構;然后,獲得簇放電相軌跡與快子系統的分岔曲線關系;依據位置關系和分岔來揭示簇放電的動力學機理.

3.4.1 CB

對于CB,快子系統的雙參分岔平面 (H,T)上的分岔曲線 (粗線) 和簇放電的相軌跡 (細線)如圖8(a) 所示.紅色實線是SN 分岔曲線,綠色實線是SNIC 分岔曲線,黑色實線是SupHopf 分岔曲線.CB 的相軌跡 (細線) 與分岔曲線共有A,B和C三個交點,分別對應SNIC,SupHopf 和SN,需要對A,B和C三點處的分岔分別進行分析來獲得簇放電的復雜動力學.其中,在A和C點上方的參數空間,快子系統表現出復雜的分岔,如圖8(b) 所示,與簇放電的相軌線距離較遠,不影響簇放電的動力學行為.存在余維–2 分岔點,包括退化分岔點P2[54,55],BT 和Cusp 分岔點.左、右鞍結分岔曲線相碰產生Cusp 分岔 (H≈0.322795 和T≈0.0592512).右SN 曲線 (右紅色) 從Cusp 發出,向左下運行至BT 分岔點 (H≈0.3182227 和T≈0.0552198),同時出現SupHopf 分岔曲線 (黑色) 和SHC 分岔曲線 (藍色),因此BT 點是導致SupHopf 和SHC 分岔的原因;SHC 與SNIC 曲線相交于點P2,SHC 在點P2處結束,同時SNIC 分岔曲線變為SN 分岔曲線.

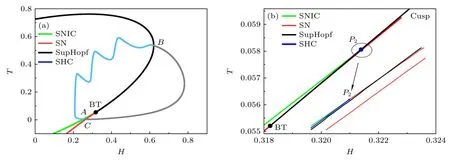
圖8 CB 的快子系統在 (H,T ) 平面上的雙參分岔和相軌跡 (a) SNIC (綠色實線)、SN (紅色實線) 和SupHopf (黑色實線) 分別代表不變環上的鞍結分岔曲線、鞍結分岔曲線和超臨界霍普夫分岔曲線,BT 代表余維–2 分岔點;淺藍色和灰色實線代表簇和休止期的相軌跡;(b) (a) 中BT 分岔點附近的放大.P2 是退化分岔點,SHC (藍色實線) 代表鞍-同宿軌分岔Fig.8.The bifurcations of fast subsystem of CB in two-parameter plane (H,T ) and the phase trajectory: (a) SNIC (green solid line),SN (red solid line) and SupHopf (black solid line) represent the saddle-node on invariant circle bifurcation curve,the saddlenode bifurcation curve and the supercritical Andronov-Hopf bifurcation curve respectively,BT represents the codimension-2 bifurcation point;the light blue and gray solid curves represent the phase trajectory of the burst and the quiescent state;(b) the enlargement near BT bifurcation point in Fig.(a).P2 is a degenerate bifurcation point,and SHC (blue solid line) represents the Saddle-Homoclinic orbit bifurcation.

在參數平面 (H,T) 上,對應A,B和C三點的T分別取值為0.00522,0.535852 和0.004636.對二維快子系統,將T分別取為A,B和C三點的值,獲得對參數H的單參數分岔,將CB 的相軌跡疊加到單參數分岔圖上,如圖9(a)—(c) 所示,能分別解釋簇放電的相軌跡在A,B和C點附近的局部動力學.從圖9(a) 可以看出,簇的起始點A距離SNIC 分岔較近;圖9(b) 中,簇的結束點B距離SupHopf 分岔較近;但是,簇放電的幅值與極限環的幅值并不對應,說明只能揭示簇的起始點和結束點附近的局部動力學.對于交點C(T≈0.004636),快慢變量分離如圖9(c) 所示,點C距離SN 分岔點比較遠,說明C點不是真正的分岔曲線和簇放電的相軌跡的交點;因此,C點對應的SN 分岔與簇放電無關.簇放電的相軌跡和余維–1 分岔曲線是否相交還要在更高維的空間內才能得到準確的認識,比如 (H,T,V) 空間內.

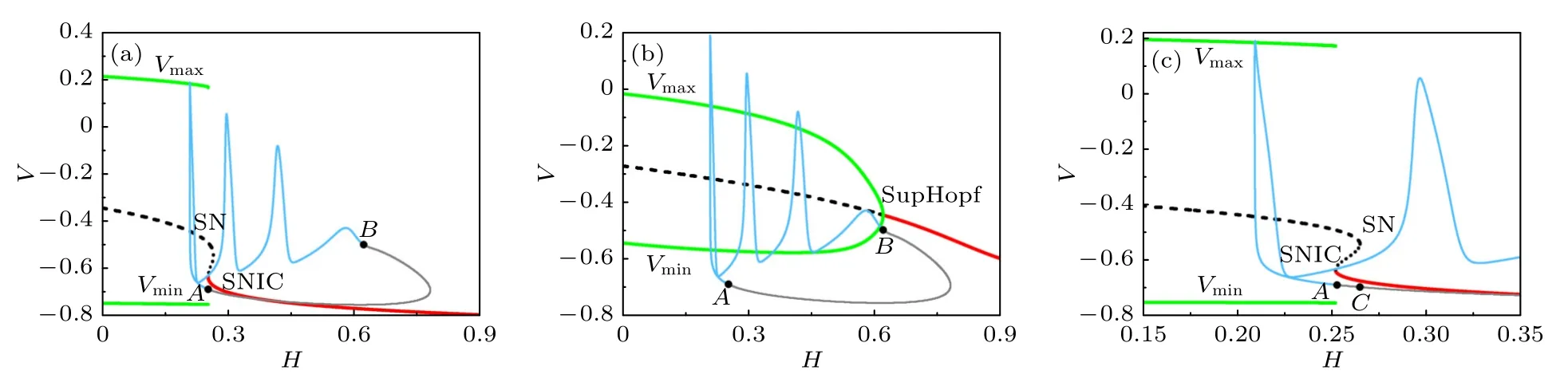
圖9 在對應A,B 和C 三個T 值處的CB 的快慢變量分離 (a) 對應CB 的起始點 A(T≈0.00522),A 點對應SNIC 分岔點;(b) 對應CB 的結束點 B(T≈0.535852),B 點對應SupHopf 分岔點;(c) 對應點 C(T≈0.004636);點C 與SN 分岔點距離較遠.淺藍色和灰色實線代表簇和休止期的相軌跡.紅色實線、黑色虛線和綠色實線分別代表穩定平衡點、不穩定平衡點和穩定極限環.SN,SNIC 和SupHopf 分別代表鞍結分岔、不變環上的鞍結分岔和超臨界霍普夫分岔Fig.9.The fast-slow variable dissection to CB at three T values corresponding to points A,B and C: (a) Corresponding to initial point A of CB (T≈0.00522).Point A corresponds to the SNIC bifurcation point;(b) corresponding to termination point B of CB(T≈0.535852).Point B corresponds to the SupHopf bifurcation point;(c) corresponding to point C (T≈0.004636).Point C is far away from the SN bifurcation point.The light blue and gray solid curves represent the phase trajectory of burst and quiescent state,respectively.The red solid curves,black dashed curves,and green solid curves represent the stable equilibrium points,the unstable equilibrium points,and the stable limit cycle,respectively.SN,SNIC,and SupHopf represent the saddle-node bifurcation,the saddle-node on invariant circle bifurcation,and the supercritical Andronov-Hopf bifurcation,respectively.

為全面和準確揭示簇放電的相軌跡和快子系統的分岔的關系,在三維空間 (H,T,V) 中,將CB的相軌跡與快子系統的分岔疊加,如圖10(a)—(d)所示.如圖10(a) 所示,藍色、黃色和粉色曲面構成平衡點曲面,對應不穩定焦點、鞍點和穩定結點,上、下綠面代表穩定極限環的極大值 (Vmax) 和極小值 (Vmin),綠、紅和黑粗線分別代表SNIC,SN和SupHopf 分岔曲線 (局部放大見圖10(b)—(d)),黑色細線代表CB 的相軌跡.可以看出,簇內峰的幅值與極限環的幅值 (綠面) 也是基本符合的,說明簇放電確實與快子系統的放電有關;簇放電的休止期與粉色面 (靜息) 很近,說明簇放電確實與快子系統的靜息有關.

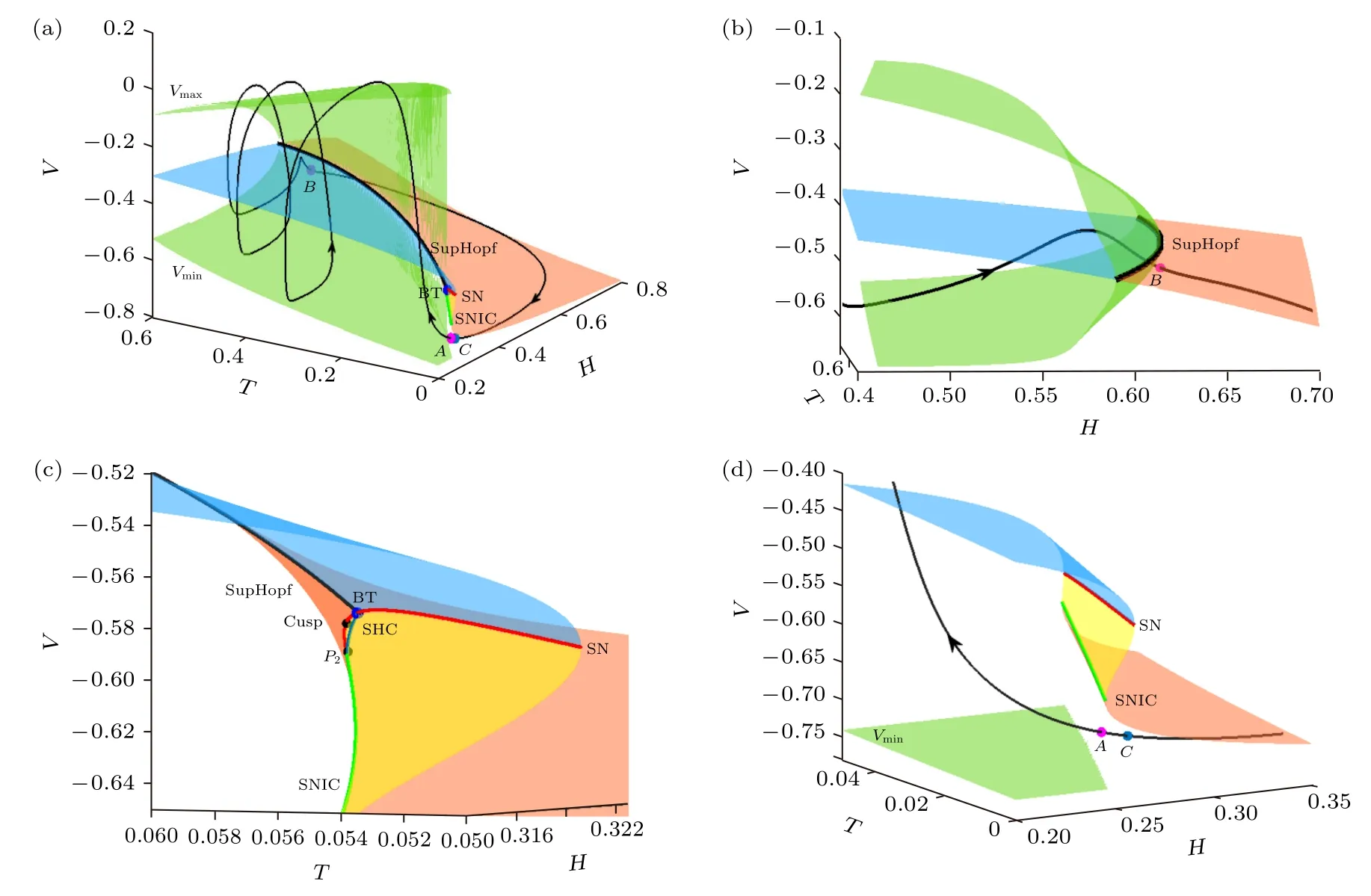
圖10 (H,T,V) 空間中CB 的雙參分岔和相軌跡.藍色、黃色和粉色面分別由不穩定焦點、鞍點和穩定結點構成,紅色、綠色、黑色粗線分別代表鞍結 (SN) 分岔、不變環上的鞍結 (SNIC) 分岔和超臨界霍普夫 (SupHopf) 分岔,上、下綠面代表穩定極限環的極大值 (Vmax) 和極小值 (Vmin),黑色細線代表簇的相軌跡 (a) 全圖;(b) 圖(a)中B 點附近的放大圖,B 點位于SupHopf 分岔曲線正下方,對應簇的結束相位;(c) 圖(a)中BT 分岔點附近的放大;(d) 圖(a)中A 點和C 點附近的放大,A 點在SNIC 分岔曲線正下方,對應CB 軌跡的起始相位,C 點距離SN 分岔曲線較遠Fig.10.Two-parameter bifurcation of fast system and phase trajectory of CB in the (H,T,V ) space.The blue,yellow,and pink surfaces are composed of the unstable focus,the saddle and the stable node,respectively.The red,green,and black thick curves represent the saddle-node (SN) bifurcation,the saddle-node on invariant circle (SNIC) bifurcation,and the supercritical Andronov-Hopf (SupHopf) bifurcation.The upper and lower green surfaces represent the maximum value (Vmax) and the minimum value(Vmin) of the stable limit cycle,respectively,and the black thin curve represents the phase trajectory of the bursting: (a) Global view;(b) the enlargement near point B in Fig.(a),point B is located just below the SupHopf bifurcation curve,corresponding to the termination phase of the burst;(c) the enlargement near BT bifurcation point in Fig.(a);(d) the enlargement near points A and C in Fig.(a).The point A is just below the SNIC bifurcation curve,corresponding to the start phase of burst,and point C is far from the SN bifurcation curve.

圖10(b) 為簇的結束點B附近的放大,可以發現,簇的結束B靠近黑粗線SupHopf 分岔,但略有偏差,說明簇放電結束于SupHopf 分岔,但因慢變量不夠慢使得結束點與分岔點有些許偏差.簇的起始點A和簇放電的相軌跡的關系見圖10(c),(d)(圖10(a)的局部放大).余維–2 分岔BT,以及余維–1 分岔SNIC,SupHopf,SN 和 SHC 等的空間位置關系清晰可見,如圖10(c) 所示.圖10(d) 中,簇的起始點A與SNIC 分岔曲線距離較近,說明簇起始于SNIC 分岔.可以明顯看出,簇放電的C點與SNIC 分岔曲線距離很遠,并無關系.

因此,與圖9 的平面圖相比,圖10 給出三維空間中CB 相軌跡與快子系統的分岔圖可以更全面認識簇放電的內在動力學: 簇與快子系統的放電有關,休止期與靜息有關;簇的起始與SNIC 分岔有關,結束與SupHopf 有關;簇放電與SN 分岔無關,雖然平面圖 (圖9) 提示SN 分岔曲線與簇放電相軌跡相交,但實際上在三維空間并不相交.因此,在三維參數空間 (H,T,V) 中,簇放電的動力學和快子系統的分岔能更為全面和準確的識別簇放電動力學.

3.4.2 IB

對于IB 平面上獲得快子系統的分岔類似于CB,如圖11(a),(b) 所示.紅色、綠色和黑色實線分別對應SN,SNIC 和SupHopf 分岔曲線.IB 的簇 (藍色線) 和休止期 (灰色線) 的相軌跡位于雙參分岔圖的左下角,即BT 分岔點的左下方.圖11(b)為圖11(a) 的放大,并且將放電區域標記為藍色,空白色區域對應靜息態.IB 的相軌跡順時針穿過SNIC 和SN 曲線,共有A,B,C和D四個交點.點A和B對應SNIC 分岔,點C和D對應SN 分岔.

同樣,為探究IB 的簇的起始與結束,需要對4 個交點處的分岔單獨進行分析.在 (H,T) 平面上,圖11(b) 中A,B,C和D四個交點處的T值分別為0.003489,0.178687,0.138212 和0.025683.在A,B,C和D四個點,將IB 的軌線疊加到二維快子系統隨H變化的分岔圖上,如圖12(a)—(d)所示.圖12(a) 中,簇的起始點A與SNIC 相匹配,簇的休止期與靜息有關,并且首個峰的幅度可以很好地用快子系統的分岔來解釋,但是無法解釋簇的結束.簇的結束相位B點與SNIC 分岔點相近但略有差距,是因為慢變量不夠慢導致的.從圖12(c),(d) 可以看出,點C和點D距離SN 分岔點都較遠,說明簇放電與SN 無關.該結果僅能解釋IB 起始和結束相位附近的局部動力學.

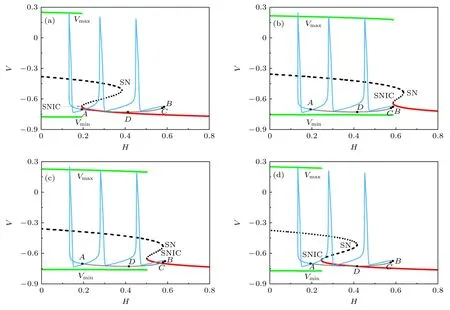
圖12 在對應A,B,C 和D 四個T 值處IB 的快慢變量分離,紅色實線、黑色虛線和綠色實線分別代表穩定平衡點、不穩定平衡點和穩定極限環,SN,SNIC 和SupHopf 分別代表鞍結分岔、不變環上的鞍結分岔和超臨界霍普夫分岔.淺藍色和灰色實線代表IB 的相軌跡 (a) 對應點 A(T≈0.003489,簇的起始相位);(b) 對應點 B(T≈0.178687,簇的結束相位);(c) 對應點 C(T≈0.138212,距離SN 分岔曲線較遠);(d) 對應點 D(T≈0.025683,距離SN 分岔曲線較遠)Fig.12.The fast-slow variable dissection to IB bursting at four T values corresponding to points A,B,C and D.The red solid curve,the black dashed curves,and the green solid curves represent the stable equilibrium point,the unstable equilibrium point,and the stable limit cycle,respectively.SN,SNIC,and SupHopf represent the saddle-node bifurcation,the saddle-node on invariant circle bifurcation,and the supercritical Andronov-Hopf bifurcation,respectively.The light blue,and gray solid curves represent the phase trajectory of IB: (a) Corresponding to point A(T ≈ 0.003489,the start phase of burst);(b) corresponding to point B(T≈0.178687,the termination phase of burst);(c) corresponding to point C(T≈0.138212,far from the SN bifurcation curve);(d) corresponding to point D(T≈0.025683,far from the SN bifurcation curve).

在三維空間 (H,T,V) 中,IB 的相軌跡和快子系統的分岔之間的關系如圖13(a),(b) 所示,圖13(b) 為圖13(a) 的局部放大.平衡點曲面為“Z”型,右下方粉色區域對應靜息狀態,中支黃色區域對應鞍點,上支藍色區域對應不穩定的焦點;上、下兩個綠面對應穩定極限環的最大值 (Vmax)和最小值 (Vmin);中支與下支平面的交線 (綠色)對應SNIC 分岔曲線,中支與上支平面的交線 (紅色) 對應SN 分岔曲線.黑色細線代表IB 的相軌跡.點A,B,C和D對應圖11(b) 中的4 個交點.如圖13(a) 所示,簇放電的峰的幅值與快子系統的極限環的幅值相對應,簇放電的休止期與快子系統的靜息 (粉色曲面) 相對應.

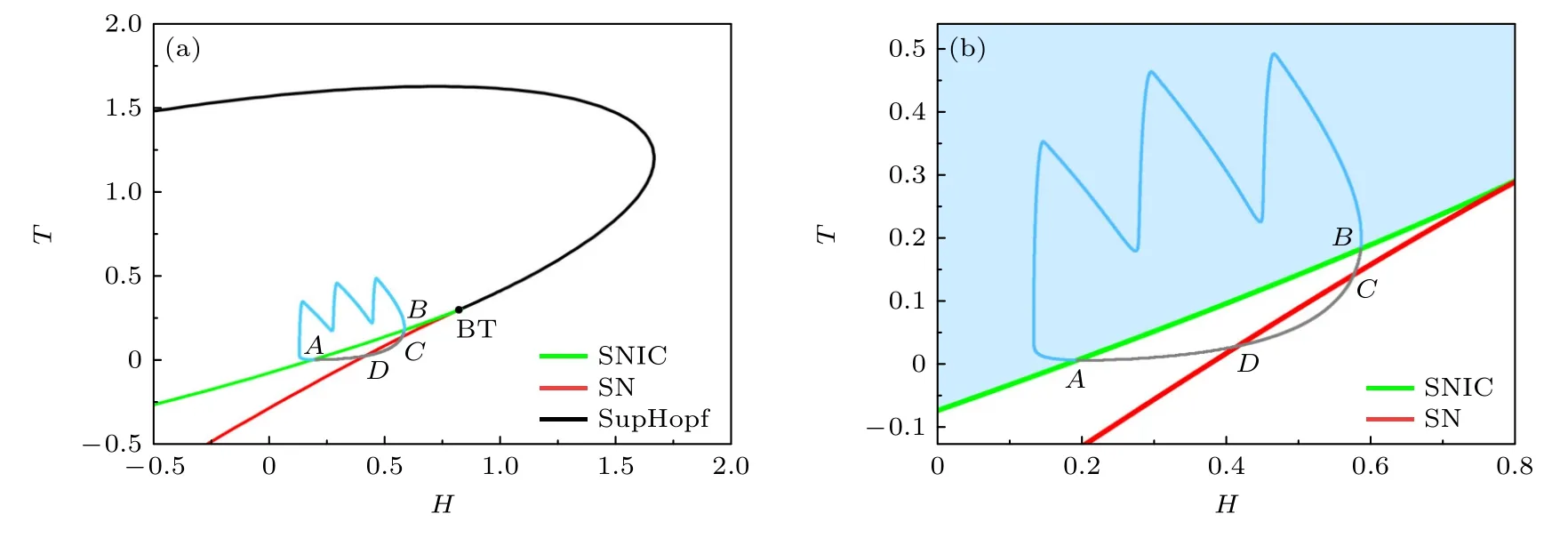
圖11 (H,T) 平面上的IB 的相軌跡與快子系統的分岔,淺藍色和灰色實線代表簇和休止期的相軌跡 (a) SNIC (綠色實線)、SN (紅色實線) 和SupHopf (黑色實線) 分別代表不變環上的鞍結分岔曲線、鞍結分岔曲線和超臨界霍普夫分岔曲線,BT 代表余維–2 分岔點 (Bogdanov-Takens);(b)圖11(a) 中IB 相軌跡附近的放大圖,藍色區域對應放電區域,空白區域對應靜息態Fig.11.The phase trajectory of IB bursting and bifurcations of the fast subsystem in phase plane (H,T ).The light blue and gray solid curves represent the phase trajectory of burst and quiescent state,respectively: (a) SNIC (green solid curves),SN (red solid curves),and SupHopf (black solid curves) represent the saddle-node on invariant circle bifurcation curve,the saddle-node bifurcation curve,and the supercritical Andronov-Hopf bifurcation curve,respectively,and BT represents the codimension-2 bifurcation point (Bogdanov-Takens);(b) the enlargement around the phase trajectory of IB in Fig.11(a),the blue area corresponds to the firing behavior,and the blank area corresponds to the resting state.

如圖13(b) 所示,簇的起始點A和結束點B與SNIC 分岔曲線相近但略有距離,是慢變量不夠慢引起的;C點和D點與SN 分岔曲線較遠,說明簇放電與SN 分岔無關.

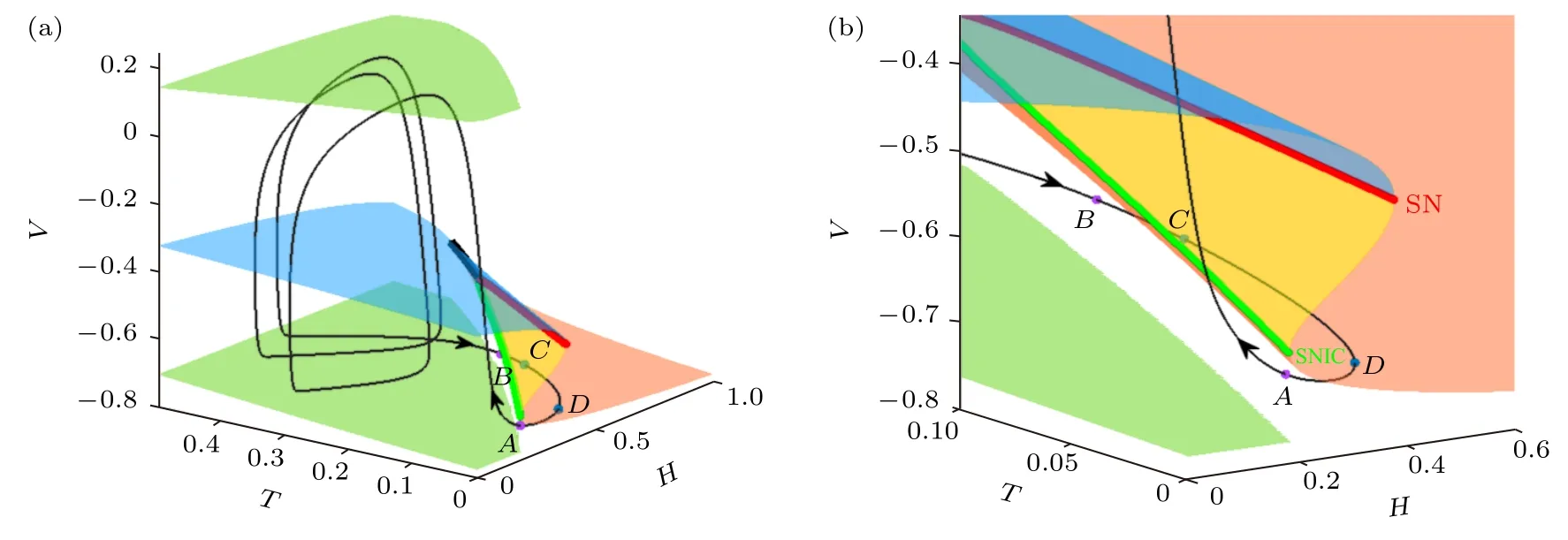
圖13 (H,T,V) 空間中快子系統的雙參分岔和IB 的相軌跡,H 和T 為慢變量,藍色、黃色和粉色面分別由不穩定焦點、鞍點和穩定結點構成,紅色和綠色粗線分別代表鞍結 (SN) 分岔和不變環上的鞍結分岔 (SNIC),上、下綠面代表穩定極限環的極大值和極小值,黑色細線代表IB 的相軌跡 (a)全圖;(b) IB 相軌跡附近的放大,點A 和點B 對應簇的起始相位和結束相位,點C 和點D 距離SN 分岔曲線較遠Fig.13.Two-parameter bifurcations of fast subsystem in the (H,T,V) space and phase trajectory of IB with H and T regarded as slow variables.The blue,yellow,and pink surfaces are composed of unstable focus,saddle,and stable node,respectively.The red and green thick curves represent the saddle-node (SN) bifurcation and the saddle-node on invariant circle (SNIC) bifurcation,respectively.The upper and lower green surfaces represent the maximum and minimum values of the stable limit cycle,and the thin black line represents the phase trajectory of IB: (a) Global view;(b) the enlargement around the phase trajectory of IB in Fig.13(a).Points A and B correspond to initial and termination phases of the burst,and points C and D are far from the SN bifurcation curve.

4 結論

新腦皮層神經元具有廣譜、重要的生理功能,表現出復雜多樣的峰和簇放電模式,依賴于神經元的類型和生理參數.揭示新腦皮層神經元放電的復雜動力學是認識其生理功能的重要環節[9].本文提出新的雙慢變量的快慢變量分離的流程,結合傳統的單慢變量的快慢變量分離方法,全面、深入地分析了新腦皮層神經元的兩類峰放電和兩類簇放電的復雜動力學,創新性體現在以下兩個方面.

一是提出了新的雙慢變量的快慢變量分離的流程.單慢變量的快慢變量分離在分析只受單個慢變量調控的簇放電或峰放電時獲得了巨大成功[9],但是,不能用于分析兩個慢變量調控的簇放電的動力學機制[28,29],因為此時快子系統含有慢變量.因此,需要根據雙慢變量的不同特征開發新的快慢變量分離方法.例如,β細胞的簇放電受到很慢和較慢的慢變量調控[28],固定很慢的慢變量為常數、然后利用較慢的慢變量為分岔參數進行快慢動力學分析.在海馬錐體神經元[29],因為兩個慢變量都很慢,將兩個慢變量都作為快子系統的分岔參數進行雙參數分岔分析;因為慢變量足夠慢,雙參數平面的分岔曲線和簇放電相軌跡的交點與簇放電全都相關.但是,對于本文研究的新腦皮層神經元的簇放電,兩個慢變量都不足夠慢,這是不同于β細胞和錐體神經元的一種新情況.因此,本文首先參照文獻[29]的流程,獲得了快子系統的雙參數平面的分岔曲線與簇放電的相軌跡的交點.與文獻[29]結果不同,部分分岔點與簇放電相關,部分不相關.進一步,本文獲得了三維空間的簇放電軌跡與快子系統的分岔曲線、平衡點曲面以及極限環的極值曲面的位置關系,依此識別了與簇放電相關的分岔,排除了與簇放電無關的分岔;與文獻[29]中分岔曲線和簇放電相軌線的交點與簇放電都相關不同.

二是全面、深入地認識了新腦皮層神經元峰放電和簇放電的動力學機制.對于峰放電,只受或主要只受一個慢變量的調控,可以利用傳統的單快慢變量分離的方法來認識峰放電 (RS 和FS) 的動力學行為,峰放電對應的軌跡只位于快子系統的放電區域內,與靜息和分岔無關.而對于簇放電,受到兩個慢變量的調控,單慢變量的快慢變量分離不能解釋CB 和IB 簇放電的動力學行為,即簇的起始和結束相位與快子系統的分岔點、簇內峰與極限環的幅值或者簇的休止期與快子系統的靜息之間不匹配.因此,將兩個慢變量H和T作為快子系統的分岔參數,獲得雙參數平面 (H,T) 上的余維–1 分岔曲線 (SNIC 和SupHopf 分岔曲線) 和余維–2 分岔點 (BT 和Cusp 分岔點),用于分析簇的起始和結束相位.CB 簇放電的相軌跡與分岔曲線相交于A,B和C三點;通過三個交點處的單參分岔分析,可知CB 簇放電軌跡的起始和結束相位僅與SNIC(A點) 和SupHopf (B點) 相關.IB 的相軌跡與分岔曲線相交于A,B,C和D四點,而簇的起始和結束僅與SNIC (A和B點) 相關.這就獲得了簇放電起始點和結束點附近的局部動力學,但是,該平面方法也有局限性: 不能認識簇內峰的幅值與穩定極限環的幅值是否匹配,以及簇放電的相軌跡與快子系統的分岔曲線的具體位置關系.因此,本文進一步分析了三維空間 (H,T,V) 中的簇放電軌跡與快子系統平衡點曲面、極限環極值曲面和分岔曲線的位置關系,進一步解釋了平面圖上SN 分岔曲線與簇放電相軌跡相交是三維空間投影導致的,排除了與簇放電無關的分岔.此外,還展示了簇與快子系統的放電有關,休止期與靜息相關.這說明,針對兩個慢變量都不足夠慢的情況,本文給出了分析其簇放電動力學行為一種有效的雙慢變量的快慢變量分離流程.

近期研究提示,針對不同的雙慢變量的快慢特征,可以發展不同的快慢變量分離法來分析簇放電的復雜動力學.本文提出了新的流程分析了兩個不足夠慢的慢變量 (T 型鈣和鈣激活鉀通道) 相關的簇放電的動力學.將利用本文的方法研究Wilson模型在不同參數下的不同放電的復雜動力學,將研究不同調控下 (如不同電流、突觸流、自反饋等) 的簇放電的復雜動力學,以及如何調控快子系統的分岔點來影響簇放電的動力學行為.進一步,還可以基于雙慢變量的快慢變量分離法研究Wilson 模型在網絡中的復雜動力學.