正常色散高非線性石英光纖優化設計及平坦光頻率梳產生*

王佳強 吳志芳 馮素春

(北京交通大學光波技術研究所,全光網絡與現代通信網教育部重點實驗室,北京 100044)

本文對一種纖芯折射率分布呈三角形的四包層結構正常色散平坦高非線性石英光纖進行優化設計,用于平坦光頻率梳產生.研究了光纖各包層寬度和折射率大小對光纖色散特性、截止波長的影響.經過優化設計的光纖在波長 1400—1700 nm 范圍內可實現較為平坦的近零正常色散,色散范圍為 -3—0 ps/(km·nm).光纖有效模場面積約為 11 μm2,非線性系數可達 12.8 W-1·km-1.基于電光調制脈沖泵浦正常色散平坦高非線性石英光纖,進行平坦光頻率梳產生仿真.研究了光纖長度、二階色散、三階色散、脈沖峰值功率、脈沖寬度、脈沖初始啁啾、脈沖形狀等參數對光頻率梳產生的影響.仿真結果有利于促進正常色散高非線性石英光纖的國產化及其在平坦光頻率梳的應用.

1 引言

近年來,光頻率梳光源在高速光通信、光譜檢測、激光雷達、微波光子學等領域得到了廣泛應用,吸引了國內外眾多研究者的關注[1].本文針對應用于光通信系統的頻率間隔為10—50 GHz 的光頻率梳展開討論和研究,這類光頻率梳應用不要求實現自參考(self-referenced).超大容量相干光通信系統對光頻率梳光源具有如下要求: 1) 為了匹配波分復用信道,要求光頻率梳梳齒間隔在10 GHz以上;2) 為了提高多通道之間的一致性,要求光頻率梳光譜平坦度較好(3 dB 以內);3) 為了增加通信容量,要求光頻率梳光譜范圍覆蓋多個通信波段(如C+L 波段);4) 為了提高單個載波調制格式的復雜度,要求光頻率梳相干性高、梳齒線寬窄(百kHz)、信噪比高等.目前傳統半導體鎖模激光器、光學Kerr 微腔、電光調制器級聯、超連續譜展寬等方法實現的光頻梳光源都已應用于大容量高速光通信實驗[2?4].傳統半導體鎖模激光器中的激光線寬在1—20 MHz 量級,需要進一步壓窄線寬;光學Kerr 微腔光梳需要精密調諧泵浦激光波長與微腔諧振頻率,長期穩定工作存在一定的難度;基于電光調制器級聯產生的光頻率梳帶寬僅約20 nm.而利用電光調制經脈沖壓縮后輸入高非線性光纖,基于超連續譜展寬實現的光頻率梳,其具有頻率間隔可調諧(10—50 GHz 可調),功率平坦度好(3 dB 以內),每個光頻梳梳齒線寬較窄的特點.2013 年美國普渡大學、加州UCSD 大學分別利用電光調制結合非線性超連續譜展寬實現了平坦光頻率梳[5,6].美國普渡大學通過引入基于空間光調制器的脈沖整形器,加州UCSD 大學通過引入非線性光纖環鏡和非線性放大光纖環鏡,利用脈沖整形方法實現了光頻率梳平坦度提升.華中科技大學[7]、哈爾濱工業大學[8]、中國科學院半導體研究所、吉林大學[9],國防科技大學[10]等先后利用單頻激光經過電光調制器得到頻率間隔10—50 GHz的可調諧電光調制光頻率梳,然后利用高非線性光纖實現超連續譜光頻率梳.然而基于超連續譜展寬的平坦光頻率梳產生機理,光頻率梳平坦度進一步提升的原因,各項參數對光頻率梳產生的影響等并沒有較為系統的研究.

基于高非線性光纖產生平坦光頻率梳,關鍵器件在于正常色散高非線性光纖.研究者們對正常色散非線性光子晶體光纖進行了研究,但光子晶體光纖制造相對繁雜[11].研究者們對正常色散非石英基光纖,如碲酸鹽[12]、硅酸鉛光纖[13]展開了研究,但目前此類光纖損耗相對較大.對于正常色散高非線性石英基光纖,長飛光纖光纜股份有限公司生產的高非線性石英光纖采用三包層折射率分布結構,色散斜率較大,不利于平坦光頻率梳的產生.四包層折射率分布結構高非線性光纖可以實現平坦近零正常色散.OFS、住友生產的色散平坦高非線性光纖采用階躍型折射率分布[14],存在近零色散正負色散波動問題,需要施加應力調控[6].筆者團隊前期對纖芯呈階躍型折射率分布的四包層高摻鍺高非線性石英光纖進行了優化設計[15],但是階躍型折射率分布四包層石英光纖的纖芯制作容差較小(因最內層纖芯半徑較小且對色散影響較大).并且對纖芯呈拋物線折射率分布的四包層石英光纖也進行了優化設計[16],但是拋物線系數不易選擇.本文對四包層高摻鍺石英光纖進行了進一步優化設計,纖芯采用三角形折射率分布,方便石英光纖參數設定和制造.另外,基于電光調制脈沖泵浦正常色散平坦高非線性石英光纖,進行平坦光頻率梳仿真,明確了平坦光頻率梳產生的原理,解釋了光頻率梳平坦性可進一步提升的原因,研究了各項參數對光頻率梳產生的影響.

2 光纖結構設計與色散優化

2.1 光纖折射率基本結構

圖1 所示為一種纖芯折射率呈三角形的四包層高摻鍺正常色散平坦高非線性光纖結構及折射率分布.如圖1(a)所示,此四包層光纖有2 個高折射率區和2 個低折射率區,光纖的最外包層材料為純石英.可分別通過摻鍺或摻氟改變各包層折射率,摻鍺的石英材料隨波長變化的折射率由Sellmeier 公式給出[15].圖1(b) 給出了三角形四包層光纖的折射率分布函數.定義相對折射率差為Δnx=,x分別取1,2,3,4,其中 Δnx分別表示光纖中各包層相對于外包層的相對折射率差.同時,定義相對折射率差區域的寬度Δry,y分別取1,2,3,4,其中,r1,r2,r3,r4,rclad分別表示光纖中三角形折射率分布的纖芯和4 個包層的半徑,Δr1為第一個正相對折射率差區域的寬度,Δr1=r1,Δr2為第一個負相對折射率差區域的寬度,Δr2=r2-r1,Δr3為第二個正相對折射率差區域的寬度,Δr3=r3-r2,Δr4為第二個負相對折射率差區域的寬度,Δr4=r4-r3.

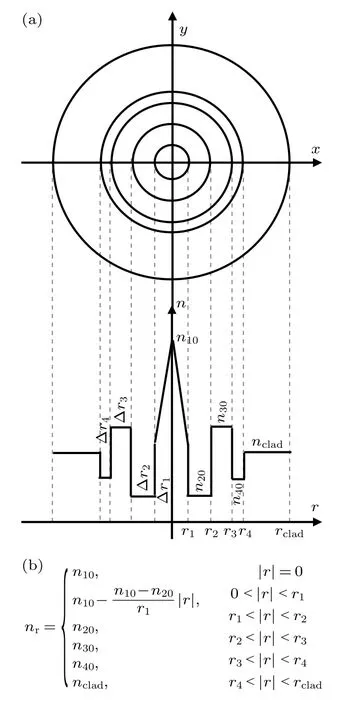
圖1 正常色散平坦高非線性光纖 (a) 光纖結構;(b) 折射率分布Fig.1.Flat normal dispersion high nonlinear fiber: (a) Structure;(b) refractive index distribution.

光纖中的群速度色散D主要由材料色散和波導色散構成,其公式為

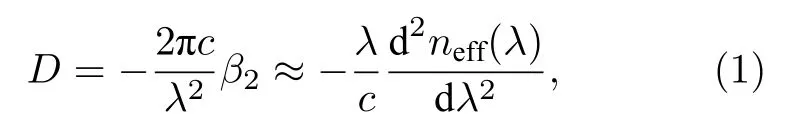
其中neff(λ)表示工作波長為λ的基模的有效折射率,c為真空中的光速,β2表示二階群速度色散.為了在 1 550 nm 附近獲得較為平坦的正常色散特性并且滿足單模傳輸條件,可以通過調節光纖中各包層的折射率和寬度,來調整光纖橫截面的折射率分布.本文通過有限元法進行數值模擬,研究纖芯三角形四包層光纖結構中的多個可控自由變量對光纖特性的影響,研究了光纖結構在各包層相對折射率變化±4% 左右,各包層相對寬度變化±1% 左右情況下的色散曲線變化情況,并分別對各自由變量研究結果進行討論分析.

2.2 各包層相對折射率變化對光纖色散特性的影響

由于多包層光纖可變參數較多,對各包層寬度和折射率進行一定的參數掃描和優化,獲得預期可實現正常色散高非線性石英光纖的參數.需要注意的是,光纖各包層折射率差需要滿足一定的條件,才能在1550 nm 附近較寬的波長范圍內得到平坦的色散特性曲線.為了實現高非線性光纖,其須具有較小的有效模場面積.因此,在多包層光纖設計中,纖芯折射率與外包層的相對折射率差須大于1 %,第一個負折射率下陷區域與外包層的相對折射率差須小于 -0.5%.首先研究在保持光纖各包層相對寬度為: Δr1=1.8 μm,Δr2=3.8 μm,Δr3=1.5 μm,Δr4=4 μm,即r1=1.8 μm,r2=5.6 μm,r3=7.1 μm,r4=11.1 μm,rclad=62.5 μm 不變的情況下,纖芯和各包層相對折射率變化對光纖色散特性的影響,結果如圖2 所示.

圖2(a)表示保持 Δn2=-0.48%,Δn3=0.4%,Δn4=-0.05% 不變的情況下,光纖三角形纖芯相對外包層的相對折射率差改變,即 Δn1取值分別為2.3%,2.35%,2.4%,2.45%,2.5% 時,光纖色散特性曲線隨波長變化的趨勢.由圖2 可知,纖芯的相對折射率越高,即 Δn1越大,光纖的色散值越大,色散曲線會由正常色散區向反常色散區整體上移.

圖2(b)表示保持 Δn1=2.45%,Δn3=0.4%,Δn4=-0.05% 不變的情況下,第一個折射率下陷區域相對外包層的相對折射率差改變,即 Δn2的值分別取 -0.6%,-0.7%,-0.8%,-0.9%,-1% 時,光纖色散特性曲線隨波長變化的趨勢.由圖2(b)可知,Δn2取值越小,即 Δn2的絕對值越大,光纖在此包層的折射率下陷越深,光纖的色散值越大,色散曲線會由正常色散區向反常色散區整體上移,其對色散調控的影響程度次于 Δn1.

圖2(c)表示保持 Δn1=2.45%,Δn2=-0.8%,Δn4=-0.05% 不變的情況下,第二個折射率凸起區域相對外包層的相對折射率差改變,即Δn3的值分別取 0.3%,0.35%,0.4%,0.45%,0.5% 時,光纖色散特性曲線隨波長變化的趨勢.由圖2(c)可知,Δn3越小,光纖在長波長處的色散值越大,色散曲線會由正常色散區向反常色散區整體上移.色散值總體上變化不大,主要是用來控制截止波長實現單模傳輸(見后文仿真分析).

圖2 各包層相對折射率變化對光纖色散特性的影響 (a) 改變△n1;(b) 改變△n2;(c) 改變△n3;(d) 改變△n4Fig.2.Effect of relative refractive index change of each cladding on fiber dispersion characteristics: (a) Changing △n1;(b) changing △n2;(c) changing △n3;(d) changing △n4.

圖2(d)表示保持 Δn1=2.45%,Δn2=-0.8%,Δn3=0.45% 的情況下,第二個折射率下陷區域相對外包層的相對折射率差改變,即 Δn4的值分別取-0.045%,-0.05%,-0.055%,-0.06%,-0.065% 時,光纖色散特性曲線隨波長變化的趨勢.由圖2(d)及其插圖可知,當 Δn4改變時,光纖的色散曲線變化不明顯.第二個折射率下陷區域的主要作用是束縛住上一層的光,防止光從第2 個高折射率區域泄露.

由以上結果可知,光纖各包層的相對折射率差的變化對光纖色散特性的影響為: Δn1對光纖色散影響最大,Δn1越大光纖色散曲線上移,特別是長波長處更加明顯;Δn2對色散的影響次于 Δn1,Δn2的絕對值越大,光纖色散曲線總體上移;Δn3,Δn4對光纖色散的長波長處有微調效果.

2.3 各包層相對寬度變化對光纖色散特性的影響

接著研究在保持光纖各包層相對折射率為:Δn1=2.45%,Δn2=-0.8%,Δn3=0.45%,Δn4=-0.05% 不變的情況下,纖芯和各包層相對寬度變化對光纖色散特性的影響,結果如圖3 所示.

圖3(a)表示保持 Δr2=3.8 μm,Δr3=1.5 μm,Δr4=4 μm 不變的情況下,光纖三角形纖芯半徑改變時,即 Δr1取值分別為 1.78 μm,1.79 μm ,1.8 μm,1.81 μm,1.82 μm 時,光纖色散特性曲線的變化情況.由圖3(a)可知,纖芯的半徑越大,即 Δr1越大,光纖的色散值越大,色散特性曲線由正常色散區域向反常色散區域整體向上偏移.

圖3(b)表示保持 Δr1=1.8 μm ,Δr3=1.5 μm ,Δr4=4 μm 不變的情況下,光纖結構中第一個折射率下陷區域的寬度變化時,即 Δr2取值分別為3.2 μm,3.4 μm,3.6 μm,3.8 μm,4 μm 時,光纖色散特性曲線的變化情況.由圖3 可知,當 Δr2增大時,光纖的色散曲線在 1 500 nm 以上的長波長區有明顯效果,Δr2增大,光纖的色散值在長波長處越大.此時,光纖的色散特性曲線由此表現出更為平坦的特性.但是,第一個折射率下陷區域的寬度不是越寬越好,太寬的下陷區會劣化光纖的抗彎曲損耗能力[17].故在優化設計光纖的長波長處的色散分布情況時,兩個高折射率區域間的距離需要格外注意.

圖3(c)表示保持 Δr1=1.8 μm ,Δr2=3.4 μm,Δr4=4 μm 不變的情況下,光纖中第二個折射率凸起區域的寬度變化時,即 Δr3取值分別為 1 μm,1.5 μm,2 μm,2.5 μm,3 μm 時,光纖色散特性曲線的變化情況.由圖可知,Δr3增大時,色散在長波長處略有減小.

圖3 各包層相對寬度變化對光纖色散特性的影響 (a) 改變Δr1;(b) 改變Δr2;(c) 改變Δr3;(d) 改變Δr4Fig.3.Effect of relative width variation of each cladding on fiber dispersion characteristics: (a) Changing Δr1;(b) changing Δr2;(c) changing Δr3;(d) changing Δr4.

圖3(d)表示保持 Δr1=1.8 μm,Δr2=3.4 μm ,Δr3=1.5 μm 不變的情況下,光纖中第二個折射率下陷區域的寬度變化時,即 Δr4取值分別為 2 μm ,3 μm,4 μm,5 μm,6 μm 時,光纖色散特性曲線的變化情況.由圖3(d)及其插圖可知,當 Δr4改變時,光纖的色散曲線變化不明顯.

由以上結果可知,光纖各包層寬度的變化對光纖色散特性的影響為:Δr1對光纖的色散特性起決定性作用,Δr1 變大,即光纖纖芯越寬,色散曲線上移,特別是長波長處比較明顯; Δr2主要決定光纖長波長處的色散特性,Δr2越大,色散在長波長處越大,此時光纖的色散曲線在長波長處越平坦,但是 Δr2不能過大,過寬的下陷區會嚴重劣化光纖的抗彎曲損耗能力; Δr3,Δr4對光纖色散長波長處有微調效果,同時可以改善光纖的抗彎曲損耗能力,適當增大有效模場面積,降低光纖接續損耗.

2.4 光纖截止波長

Δn1,Δn2和Δr1,Δr2對光纖色散曲線影響較大,所以通過調節 Δn3,Δn4和 Δr3,Δr4大小組合來改變該高非線性光纖的截止波長,使得光纖在1550 nm 處滿足單模傳輸條件.本文設計目標是能夠在大于 1 310 nm 的波段實現單模傳輸.

在保持 Δr1=1.8 μm,Δr2=3.8 μm,Δr3=1.5 μm,Δr4=4 μm 不變的情況下,一方面,在保持 Δn1=2.45% ,Δn2=-0.8%,Δn4=-0.05% 不變時,當 Δn3取值為 0.6% ,波長為 1 310 nm 時,在第二個折射率凸起區域會激發出穩定的高階模,模場如圖4(a)所示,這時的截止波長約為 1 400 nm .當Δn3取值為 0.45% 時,Δn3區域在波長為 1310 nm時已經不能支持高階模,由光纖截止波長理論可知,工作波長大于 1 310 nm 時都能滿足單模傳輸條件,且此時色散曲線在 1 550—1600 nm 范圍較為平坦.另一方面,保持 Δn1=2.45%,Δn2=-0.8% ,Δn3=0.45% 不變,當 Δn4取值為 -0.045% ,波長為 1 300 nm 時,在第二個折射率凸起區域也會出現較為穩定的高階模,模場如圖4(b)所示.而且此下陷包層的主要作用是束縛住上一層的光,防止光從第二個高折射率區域泄露,因此 Δn4的絕對值不可過小.

同理,在保持 Δn1=2.45%,Δn2=-0.8%,Δn3=0.45%,Δn4=-0.05% 不變的情況下,一方面,在保持 Δr1=1.8 μm,Δr2=3.4 μm ,Δr4=4 μm 不變時,當 Δr3取值為 2 μm,波長為 1310 nm時,在第二個折射率凸起區域會激發出穩定的高階模,模場如圖4(c)所示.當 Δr3取值為 1.5 μm 時,Δr3區域在波長為 1 310 nm 處已經不能支持高階模,由光纖截止波長理論可知,工作波長大于 1310 nm時都能滿足單模傳輸條件,且此時色散曲線在1550—1600 nm 范圍也較為平坦.另一方面,發現在保持 Δr1=1.8 μm,Δr2=3.4 μm,Δr3=1.5 μm不變時,當 Δr4取值為 3 μm,波長為 1 300 nm 時,在第二個折射率凸起區域也會出現較為穩定的高階模,模場如圖4(d)所示.而且此下陷包層的主要作用是束縛住上一層的光,防止光從第2 個高折射率區域泄露,因此 Δr4的寬度不可過小.

圖4 光纖中激發出的高階模場 (a) Δn3 取值過大;(b) Δn4 的絕對值過小;(c) Δr3 取值過大;(d) Δr4 取值過小Fig.4.High-order mode field excited in the fiber: (a) When Δn3 is too large;(b) when the absolute value of Δn4 is too small;(c) when Δr3 is too large;(d) when Δr4 is too small.

綜上可知,通過調整 Δn3,Δn4以及 Δr3,Δr4的參數值,可以調節光纖的截止波長,能夠在工作波長大于 1 310 nm 時實現單模傳輸,并且獲得較好的抗彎曲損耗性能.

2.5 光纖的有效模場面積和非線性系數

光纖的非線性系數γ表達式為

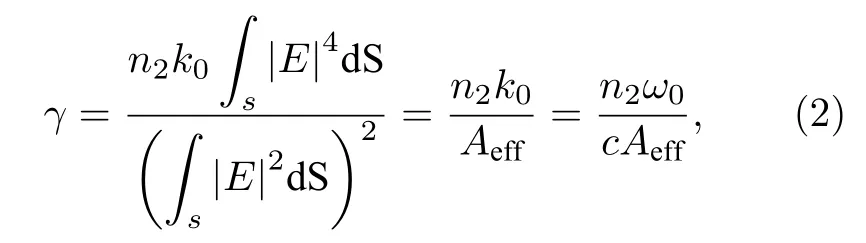
其中n2為介質的非線性折射率系數,摻鍺石英光纖中n2的值一般為 (2.16+0.033X)×10-20m2/W,X為光纖中摻鍺的摩爾濃度,ω0為角頻率.光纖的有效模場面積表達式為

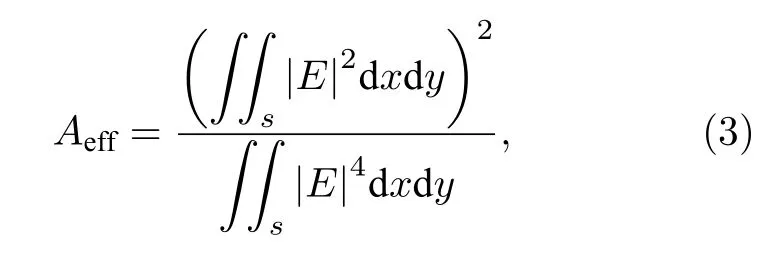
其中 |E|為電場矢量的模.

在以上參數優化設計的光纖結構基礎上,即Δn1=2.45%,Δn2=-0.8%,Δn3=0.45%,Δn4=-0.05%,Δr1=1.8 μm,Δr2=3.4 μm,Δr3=1.5 μm,Δr4=4 μm 時,光纖在 1 550 nm 附近有較好的色散平坦曲線和較大的非線性系數,圖5(a),(b)所示為最終優化設計的正常色散平坦高非線性光纖的色散,有效模場面積Aeff和非線性系數γ隨工作波長的變化曲線.在 1 400—1700 nm 之間色散范圍為 - 3—0 ps/(km·nm).在1550 nm 處,光纖有效模場面積約為 11 μm2,非線性系數可達12.8 W-1·km-1.

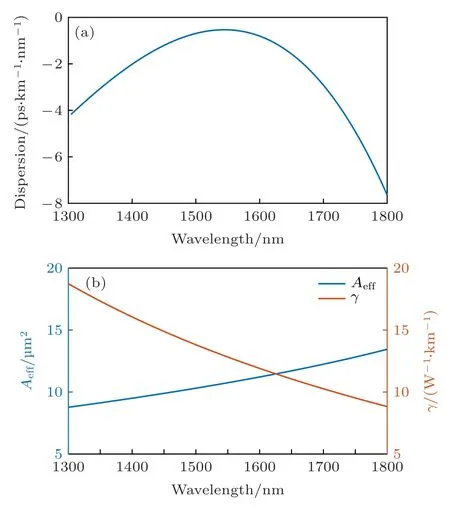
圖5 最終優化設計的正常色散平坦高非線性光纖 (a) 色散變化曲線;(b) Aeff 和 γ 變化曲線Fig.5.The final designed normal dispersion high nonlinear fiber: (a) The dispersion curve;(b) the curve of Aeff and γ.

3 基于正常色散高非線性石英光纖的平坦光頻率梳產生

利用1550 nm 波段的10—50 GHz 高重復頻率皮秒脈沖光源(可用電光調制及脈沖壓縮實現)[4?6],經高功率光纖放大器后輸入正常色散高非線性光纖,可以產生平坦光頻梳,這里選擇電光調制形成脈沖,主要考慮其可以產生10 GHz 以上重復頻率脈沖,同時方便實現重復頻率可調(調整電光調制器的調制頻率),更有可能應用于實際的高速光通信中(信道間隔在10 GHz 以上).光脈沖在正常色散平坦高非線性光纖中傳輸時,首先發生自相位調制,傳輸到一定距離后發生光波分裂,這會導致脈沖展寬,其頻譜也隨之展寬,同時頻譜包絡的平坦性變好.時域單一脈沖的頻域光譜包絡和具有一定重復頻率的周期性脈沖的光頻率梳的頻域光譜包絡是一致的[1].因此,通過研究單一脈沖的頻域光譜包絡演化情況,考察光頻率梳的平坦度和帶寬.本文利用廣義非線性薛定諤方程(generalized nonlinear Schr?dinger equation,GNLSE)分析基于正常色散高非線性光纖產生光頻梳中單一脈沖和光譜的包絡演化,即

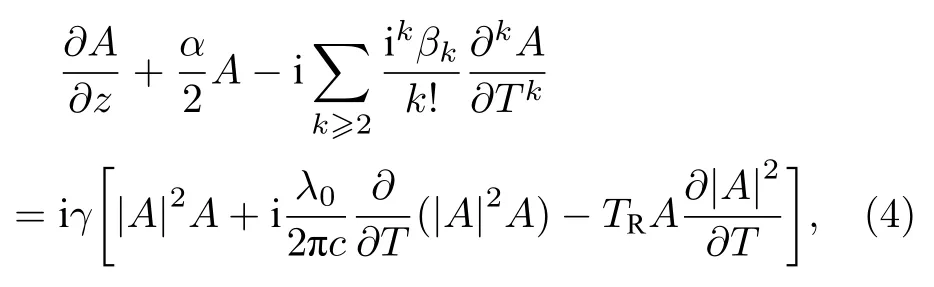
式中,λ0為脈沖中心波長,A為脈沖緩變包絡振幅,z為脈沖在光纖中傳輸的距離,βk為光纖的各階色散效應,α為光纖的損耗,TR為內脈沖拉曼散射系數.通過分步傅里葉變換算法進行數值求解,仿真中忽略了β4以上的高階色散、拉曼效應和自變抖效應.

基于第2 節中經優化設計獲得的正常近零色散平坦高非線性石英光纖的參數和實驗可實現的脈沖光源的參數[4?6](如表1 所示),利用非線性薛定諤方程,對無啁啾雙曲正割脈沖經400 m 長正常色散平坦高非線性光纖傳輸后產生光頻梳進行仿真,結果如圖6 所示.隨著傳輸距離增加,脈沖的峰值功率減小,脈沖展寬,光頻率梳頻譜也隨之展寬,頻譜包絡逐步平坦化.

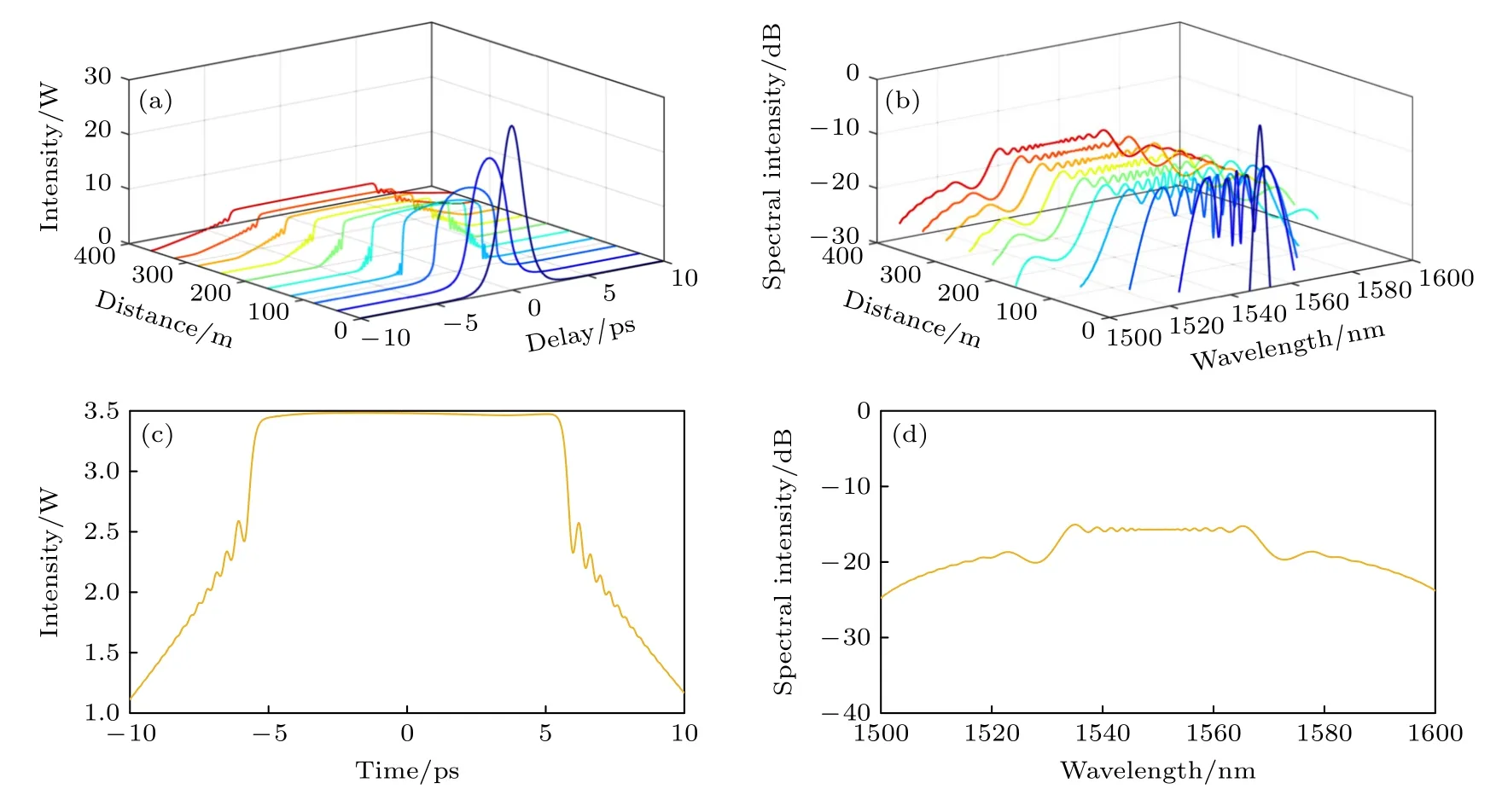
圖6 無啁啾雙曲正割光脈沖經過正常色散平坦高非線性光纖產生光頻梳 (a),(b) 傳輸不同光纖長度情況下時域和頻域包絡演化;(c),(d) 傳輸到400 m 時光頻率梳時域和頻域包絡Fig.6.The generated optical frequency comb with a non-chirped hyperbolic secant pulse propagating in flat normal dispersion high nonlinear fiber: (a),(b) Time and frequency domain envelope evolution with different propagation length;(c),(d) time and frequency domain envelope of the optical frequency comb after the pulse propagation of 400 m.

表1 仿真所采用的參數Table 1. The parameters used in the simulation.

為了更好地展示無啁啾雙曲正割脈沖在光纖傳輸過程中產生光頻率梳的時域和頻域的演化,利用交叉相關頻率分辨光學開關X-FROG (crosscorrelation frequency resolved optical gating)技術,仿真初始無啁啾雙曲正割脈沖在正常色散非線性石英光纖中傳輸0,100,200,400 m 的時譜圖如圖7 所示.脈沖傳輸至 100 m 時,脈沖寬度和光頻率梳頻譜寬度均有顯著的展寬,但光頻率梳頻譜平坦度不佳,頻譜中心振蕩明顯;當傳輸至 200 m 時,時域已經發生了光波分裂(時域脈沖邊沿有震蕩波紋),光頻率梳頻譜中心兩側的光譜開始呈現“臺階”,此時頻譜中心平坦帶寬達到最寬,頻譜中心平坦度有了明顯改善;傳輸至 400 m 時,脈沖繼續展寬,峰值功率下降,脈沖包絡與 200 m 沒有明顯差別,頻譜中心的振蕩有了一定的改善,但是平坦頻譜寬度卻有一定減小.可以推測到,此時即使再增大光傳輸距離,光頻率梳頻譜寬度也不會持續展寬,反而可能由于色散和損耗劣化光頻梳的性能.從圖7 可知,無啁啾雙曲正割脈沖主要經歷了自相位調制、光波分裂過程,傳輸長度為400 m 時,脈沖前后沿尾部存在一定的非頻移分量[18],脈沖呈現為準線性啁啾的平頂光脈沖,存在一定的非線性啁啾分量.

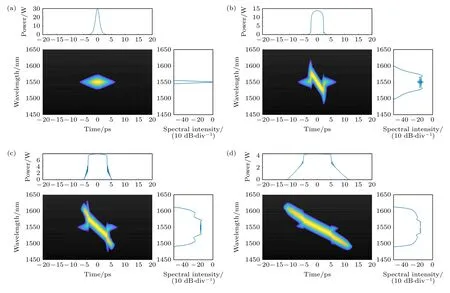
圖7 無啁啾雙曲正割光脈沖傳輸不同光纖長度產生光頻率梳的時譜圖 (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 mFig.7.Spectrograms of non-chirped hyperbolic secant optical pulses at various propagation fiber lengths: (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 m.

同時,研究了脈沖峰值功率P,脈沖半寬度T0,脈沖初始啁啾C,光纖二階色散β2,光纖三階色散β3,脈沖波形 Pulse 對光頻梳時域和頻域包絡的影響.仿真中以表1 為基準,正常色散高非線性光纖長度為 400 m ,僅改變其中一個參數,而其他參數不變,結果如圖8 所示.

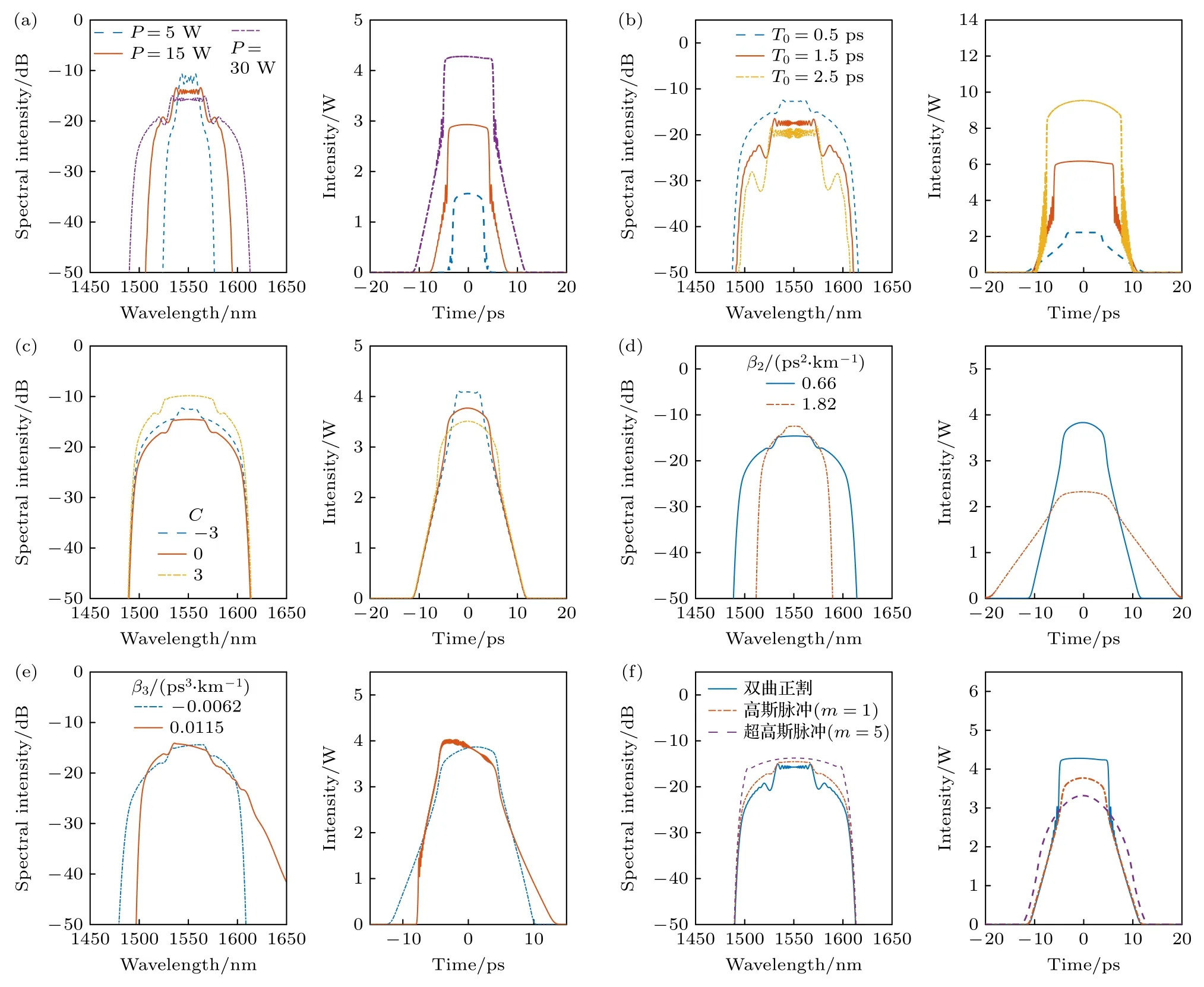
圖8 改變一個參數而其他參數不變,脈沖在傳輸400 m 光纖后展寬的光頻率梳頻譜包絡及時域波形 (a)只改變 P;(b)只改變 T0;(c)只改變 C;(d)只改變 β2;(e)只改變 β3;(f)只改變輸入脈沖波形Fig.8.The broadening optical frequency comb spectra and pulse envelope after the pulse propagates through 400 m fiber when one parameter is changed while the other parameters remain unchanged: (a) Only changeing P;(b) only changeing T0 ;(c) only changeing C;(d) only changeing β2;(e) only changeing β3;(f) only changeing the input pulse waveform.

如圖8(a)所示,以無啁啾雙曲正割脈沖為輸入波形,調節脈沖峰值功率P分別為5,15,30 W,可以看到,輸入脈沖的峰值功率越大,輸出的脈沖時域寬度越寬,峰值功率越大,且光頻梳的頻譜展寬帶寬越寬,頻譜中心波長 1 550 nm附近光頻率梳的平坦性越好.

如圖8(b)所示,以無啁啾雙曲正割脈沖為輸入波形,調節脈沖半寬度T0分別為0.5,1.5,2.5 ps,可以看到,輸入脈沖寬度越窄,輸出光頻梳的最大寬度越寬,且頻譜中心波長 1 550 nm 附近光頻梳的平坦度隨之提升.

如圖8(c)所示,以高斯脈沖為輸入波形,調節脈沖初始啁啾C分別為 -3,0,+3,可以看到,隨著啁啾參量C的增大,輸出的脈沖時域寬度越寬,與此同時,光頻梳頻譜的中心平坦度較好的展寬帶寬越寬.同時,在脈沖中引入負的初始啁啾參量(即C＜0),此時光纖的二階色散β2和初始啁啾參量C滿足β2C＜0,故時域脈沖在傳輸過程會經歷先壓縮后展寬的過程,相當于增大了光波分裂發生所要求的傳輸距離.

如圖8(d)所示,以無啁啾高斯脈沖為輸入波形,調節二階色散β2分別為 0.66 ps2/km,1.82 ps2/km,可以看到,光纖的二階色散β2越小(即越接近0),輸出的光頻梳的頻譜寬度越寬.

如圖8(e)所示,以無啁啾高斯脈沖為輸入波形,調節三階色散β3分別為 -0.0062 ps3/km ,0.0115 ps3/km,可以看到,光纖的三階色散β3絕對值越小,輸出的光頻梳平坦度和對稱性越好.同時,三階色散β3的正負代表了頻譜的傾斜方向.

如圖8(f)所示,分別以雙曲正割脈沖,高斯脈沖 (m=1) ,超高斯脈沖 (m=5) 為輸入波形,可以看到,輸入脈沖波形不同,最終光頻梳的時域波形和頻譜也不同.特別是超高斯脈沖 (m=5) 傳輸后演變為類拋物形脈沖,而其頻譜的展寬帶寬最寬,光頻梳中心平坦度明顯提升,光頻梳在整個帶寬范圍內都具有較好的平坦度.由雙曲正割脈沖產生的光頻梳平坦度最差;由高斯脈沖 (m=1) 產生的光頻梳平坦度介于兩者之間.基于雙曲正割脈沖或高斯脈沖 (m=1) 抽運可實現平坦度為3 dB,帶寬約為40 nm 的光頻率梳.基于超高斯脈沖 (m=5) 抽運可實現平坦度為2 dB,帶寬約為92 nm 的光頻率梳.

為了探究高斯脈沖,超高斯脈沖比雙曲正割脈沖生成的光頻梳的平坦度更好的原因,利用XFROG 技術對高斯脈沖 (m=1),超高斯脈沖(m=5) 在高非線性光纖中傳輸的時頻演化過程進行仿真.兩種脈沖在正常色散非線性石英光纖中傳輸0,100,200,400 m 的時譜圖分別如圖9,圖10所示.可知,高斯脈沖在傳輸過程中也經歷了自相位調制、光波分裂過程,傳輸到400 m 長度時,脈沖前后沿尾部存在的非頻移分量相比雙曲正割脈沖減少,脈沖也呈現為準線性啁啾的平頂光脈沖,存在一定的非線性啁啾分量.而超高斯脈沖在傳輸過程中幾乎沒有發生光波分裂效應,傳輸到400 m長度時,脈沖呈現為準線性啁啾的近拋物形光脈沖.我們認為光頻率梳平坦度改善的主要原因是超高斯脈沖相比高斯脈沖和雙曲正割脈沖,輸入脈沖邊沿的拖尾較小.故若選取超高斯脈沖作為輸入脈沖源,則可得到性能更佳的平坦光頻梳.可以采用商用的脈沖整形器(如Finisar 公司的WaveShaper 4000S/X)對輸入脈沖波形進行整形,實現超高斯脈沖[19],從而實現平坦度較好且帶寬也較寬的光學頻率梳.

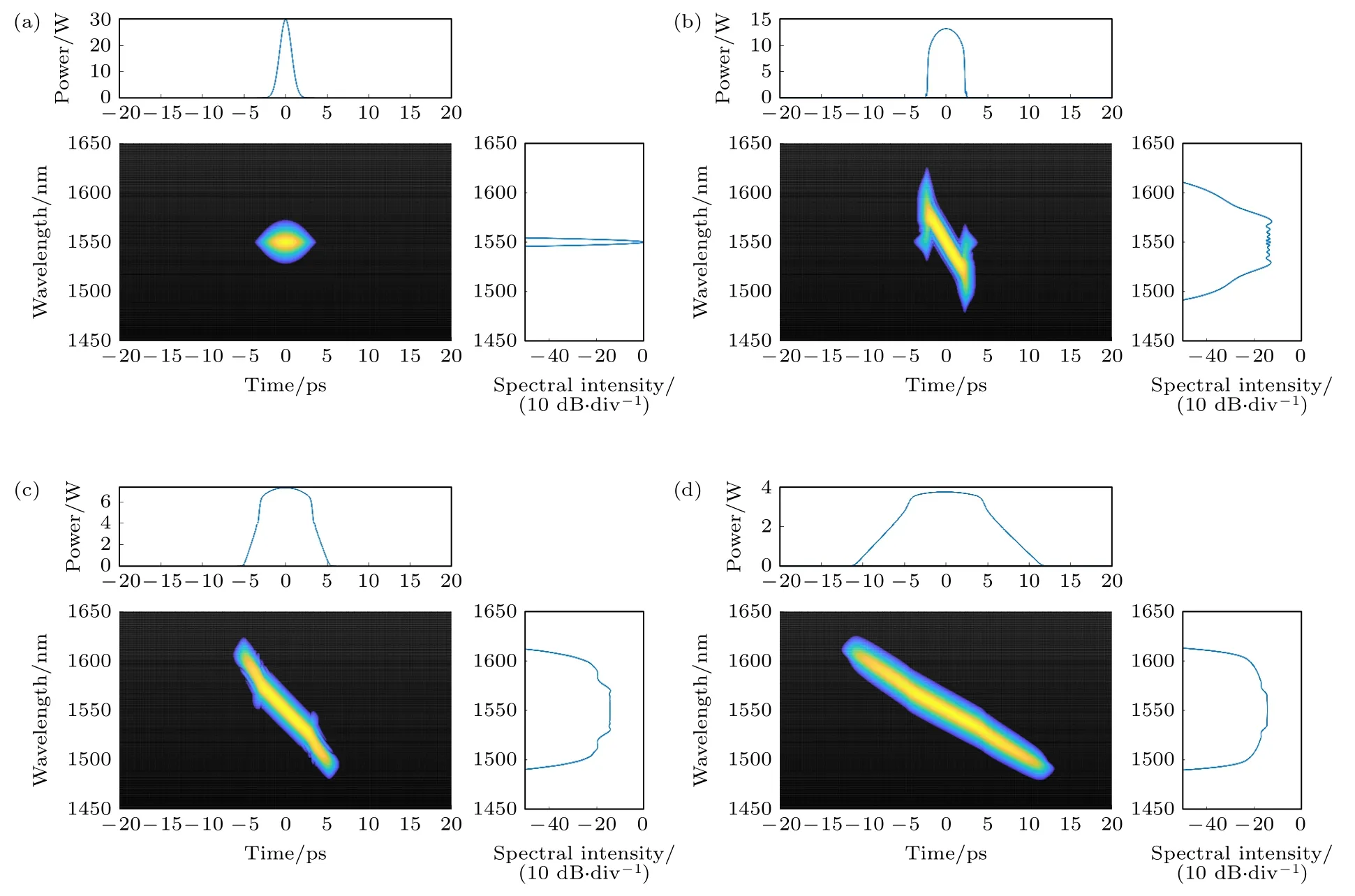
圖9 無啁啾高斯光脈沖(m=1)傳輸不同光纖長度產生光頻率梳的時譜圖 (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 mFig.9.Spectrograms of the non-chirped Gaussian pulse (m=1) at various propagation fiber lengths: (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 m.

圖10 無啁啾超高斯光脈沖(m=5)傳輸不同光纖長度產生光頻率梳的時譜圖 (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 mFig.10.Spectrograms of the non-chirped super Gaussian pulse (m=5) at various propagation fiber lengths: (a) 0 m;(b) 100 m;(c) 200 m;(d) 400 m.

4 結論

本文對一種纖芯折射率分布呈三角形的四包層結構正常色散平坦高非線性石英光纖進行了優化設計.研究了光纖各包層寬度和折射率大小對光纖色散特性、截止波長的影響.基于電光調制脈沖泵浦正常色散平坦高非線性石英光纖,進行平坦光頻率梳仿真,研究了光纖長度、二階色散、三階色散、脈沖峰值功率、脈沖寬度、脈沖初始啁啾、脈沖形狀等參數對光頻率梳產生的影響.基于雙曲正割脈沖或高斯脈沖泵浦可實現平坦度為3 dB,帶寬約為40 nm 的光頻率梳.基于超高斯脈沖泵浦可實現平坦度為2 dB,帶寬約為92 nm 的光頻率梳.故基于本文提出的正常色散高非線性光纖及光頻率梳產生研究,可實現重復頻率10 GHz 以上,功率平坦度3 dB 以內,頻譜帶寬約40—90 nm 的光頻率梳.仿真結果有利于促進正常色散高非線性石英光纖的國產化及其在平坦光頻率梳的應用.