高速動車組整備及載人狀態車體模態分析

孟林林，賈尚帥，彭壘

(中車唐山機車車輛有限公司，河北 唐山 063000)

近年來，隨著我國高速鐵路運行速度及服役時間的提高，列車振動加劇問題日益突出，這不僅會縮短列車的服役壽命，還會影響乘客乘坐舒適度甚至還可能危及乘客的人身安全[1].車體是整個列車構成中最為復雜和重要的大型結構之一，承載著列車的全部靜載荷和服役運行中的動載荷，車體結構模態對整車的動力學性能和乘坐舒適性有很大的影響[2].車體模態頻率是車體最重要的動力學參數，而模態分析是獲得該動力學參數最普遍的一種方法.近年來，眾多學者在車體模態分析方面，展開了廣泛的研究.王劍等[3]研究了車下設備吊掛參數對高速動車組車體模態的影響.王鐵成等[4]研究了車下設備安裝剛度對動車組車體模態的影響.趙士忠等[5]研究了整備狀態下的軌道交通車輛車體模態，并將人體模型簡化為單自由度的彈簧質量單元，然后進行了載人整備狀態下的車體模態分析.黃曉婷等[6]開展了鐵道客車乘客的模型建立與仿真的研究，并對所建的乘客仿真模型進行了舒適度分析.近年來，有關車體模態的分析已開展了大量的研究，但對于車體整備載人模態計算分析尤其是人體模型建立方面的研究相對較少.

因此，本文以某型號高速動車組中間車為研究對象.首先將乘客分別簡化為多質量塊-彈簧-阻尼模型和單質量塊模型，采用Hypermesh軟件建立了某高速動車組中間車載人狀態的有限元模型.然后，將建立好的有限元模型導入ABAQUS軟件，分別計算了整備未載人狀態、載人(多質量塊-彈簧-阻尼模型)狀態和載人(單質量塊模型)狀態車體的振動模態.最后分析了人體模型對車體模態的影響.

1 有限元模型建立

1.1 車體結構有限元模型

以某型號高速動車組中間車為研究對象，車體全長為25 m，寬為3.36 m，承載結構(以下稱白車體)由大型中空鋁合金擠壓型材焊接而成，鋁合金材質主要為EN AW-6005A和EN AW-6082.采用Hypermesh軟件建立白車體有限元模型，彈性模量為70 GPa，泊松比為0.33，密度為2 750 kg/m3.白車體有限元模型質量為10.87 t，與實測值11.02 t相差較小.

1.2 整備狀態車體有限元模型

采用Hypermesh軟件建立整備狀態車體有限元模型，見圖1.殼單元數量為817 532，質量點單元數量為2 509 119.有限元模型質量為36.83 t，與實測質量36.98 t相差較小.

圖1中，門窗采用殼單元，門窗與其邊框采用橡膠單元進行連接；大型車下吊掛設備采用在實際重心位置設置Mass質量點，并通過屬性為三向動剛度的彈簧單元耦合連接于車體實際安裝座位置的方法進行模擬.其他附屬設備通過在鋁合金車體實際安裝位置設置質量點的形式進行模擬.

依據TB/T 2843—2015《機車車輛用橡膠彈性元件通用技術條件》，分別對車下大型吊掛設備的減振器進行動剛度試驗.動剛度試驗在電液伺服疲勞實驗機上完成，見圖2.

減振器三向加載方式如下：

(1)Z方向(垂向)：力控制加載方式，施加簡諧動載荷，頻率取5 Hz、6 Hz、8 Hz、10 Hz、12 Hz，初始預載荷值等于車下吊掛位置安裝位置處支反力值，靜態動載荷幅值動載荷為0.2倍預加載荷；

圖2 減振器動剛度試驗

(2)X方向(縱向)：施加垂向預加位移5 mm，力控制加載方式，施加簡諧動載荷，頻率取5 Hz、6 Hz、8 Hz、10 Hz、12 Hz，初始預加靜態動載荷為0，動載荷幅值與垂向相同；

(3)Y方向(橫向)：施加垂向預加位移5 mm，力控制加載方式，施加簡諧動載荷，頻率取5 Hz、6 Hz、8 Hz、10 Hz、12 Hz，初始預加靜態動載荷為0，動載荷幅值與垂向相同.

分別對每個方向、每個頻率工況進行50次循環，之后提取5次穩定循環對應的載荷——變形數據，計算對應的動剛度值，并取平均值作為減振器的動剛度值.車下吊掛設備布置見圖3，各設備所用減振器的動剛度詳細參數見表1、表2.

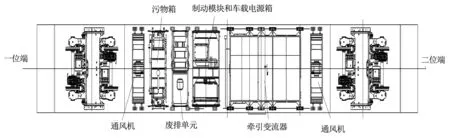
圖3 車下設備布置圖

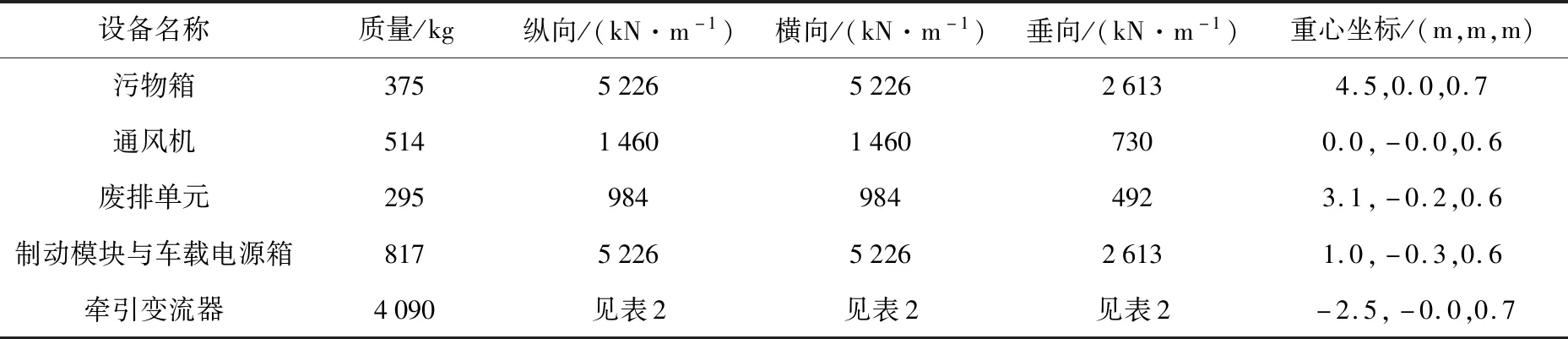
表1 大型車下吊掛設備參數(動剛度)

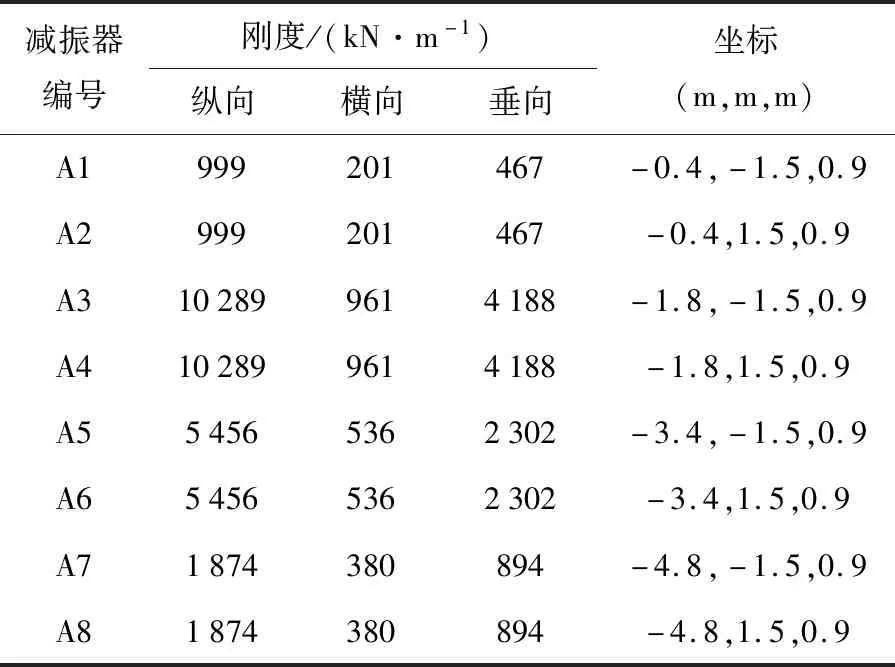
表2 牽引變流器吊掛參數(動剛度)

其中，牽引變流器采用V形減振器，其他設備采用柱形減振器，減振器結構示意圖見圖4.

(a) 柱形減振器

1.3 載人狀態車體有限元模型

本研究中人體模型及各部分連接示意圖見圖5[7]，人體模型共分為六個部分：頭、脖子、上身、下身、臀部、腿，單人總重量為80 kg.其中座椅和客室地板之間、座椅和臀部之間采用剛性連接，其余各部分之間為三向彈簧阻尼連接.

人體模型有限元模型見圖6，各部分的質量、轉動慣量及他們之間的連接剛度和阻尼用文獻[7]中的方法進行比例換算，如表3和表4所示.此外，為了對比分析不同人體模型對車體模態結果的影響，還將人體模型簡化為單質量塊模型平鋪在車體地板上，人體模型質量共7.2 t.

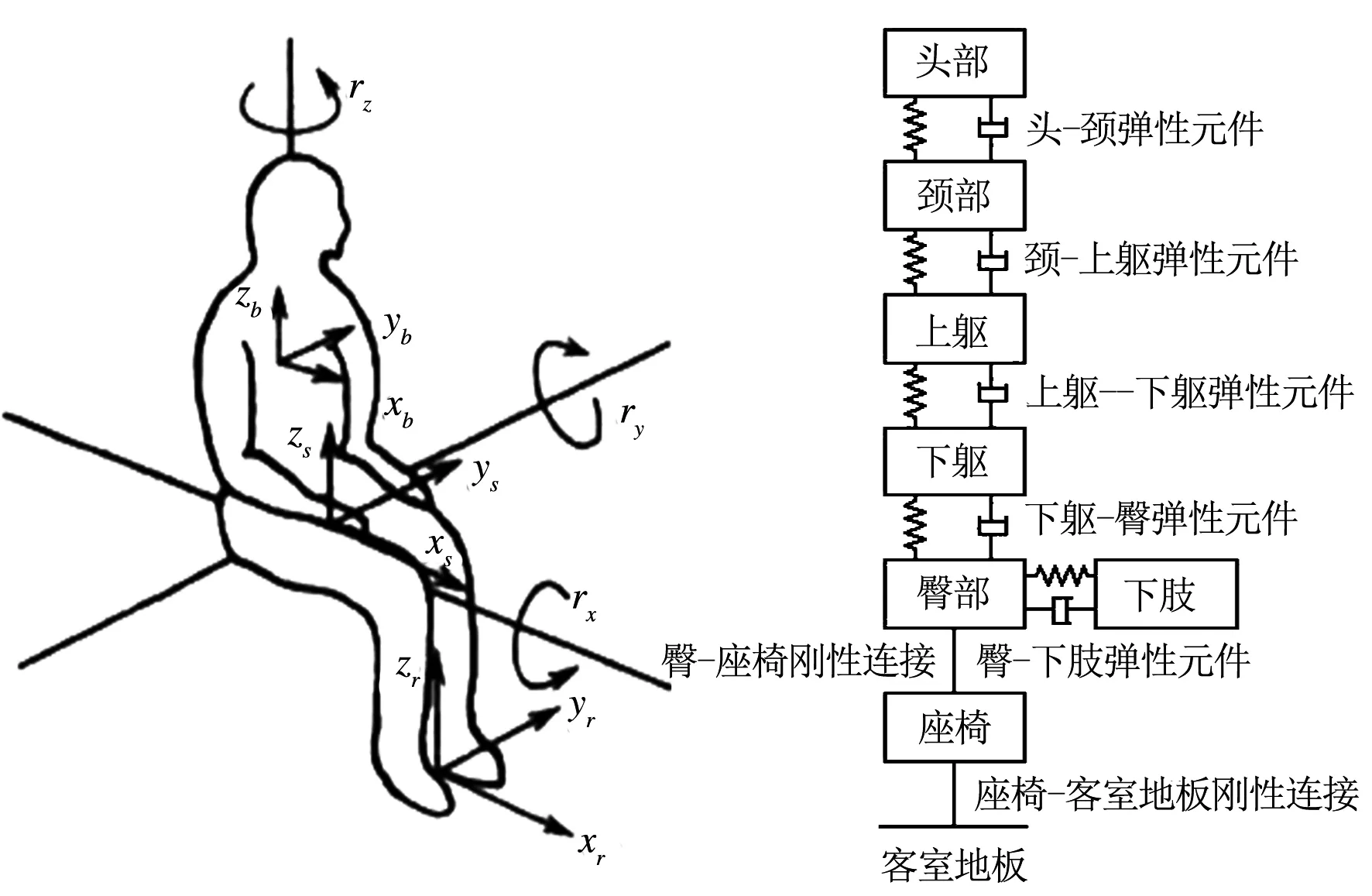
圖5 人體模型及各部分連接示意圖

圖6 人體模型有限元模型

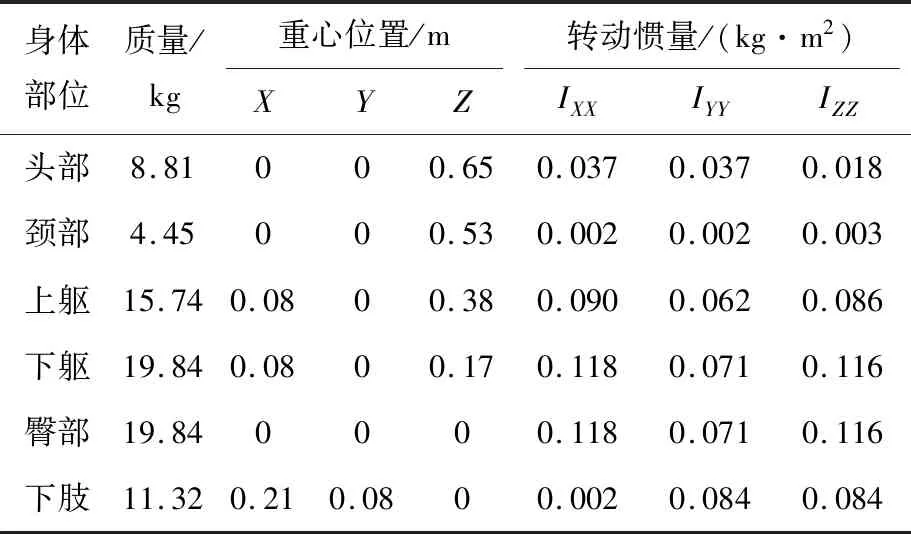
表3 人體模型質量、重心、轉動慣量參數表[7]

表4 人體模型剛度屬性表[7]

2 車體模態結果

將在Hypermesh中建立好的有限元模型導入ABAQUS軟件，分別計算了整備未載人狀態、載人(多質量塊-彈簧-阻尼模型)狀態和載人(單質量塊模型)狀態車體的振動模態.

2.1 整備狀態

整備狀態車體的一階菱形、呼吸、扭轉和垂彎四種典型振動模態云圖及對應頻率見圖7.

(a) 一階菱形，8.44 Hz

仿真與試驗結果對比見表5.階模態頻率誤差均在±10%以內，表明仿真計算模型較為合理.

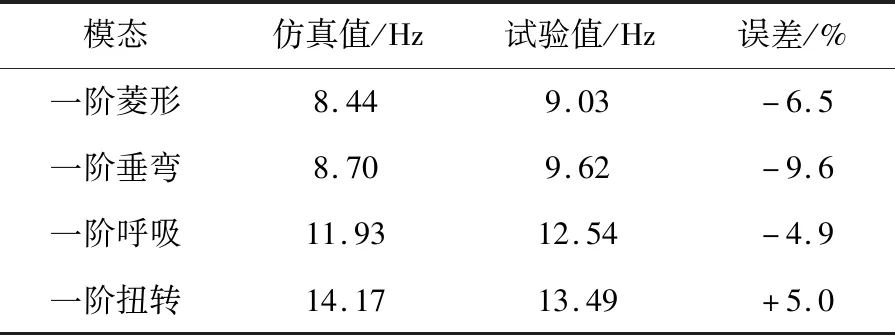
表5 整備狀態模態頻率的仿真值和試驗值

2.2 整備載人狀態

整備載人狀態(多質量塊-彈簧-阻尼模型)和整備載人狀態(單質量塊模型)車體的四種典型振動模態對應頻率見表6.

表6 整備載人狀態模態頻率 Hz

結果表明：兩種整備載人狀態車體的模態頻率均低于未載人整備狀態.采用單質量塊模型對人體模型進行建模時，車體的四種典型模態頻率較未載人狀態降低幅度大，尤其是一階垂彎頻率，降低幅度達0.92 Hz；而當采用多質量塊-彈簧-阻尼模型對人體進行簡化建模時，車體的四種典型模態頻率較未載人狀態降低幅度小，對于最為重要的一階垂彎頻率降低幅度僅為0.15 Hz.單質量塊模型相當于將人體模型直接與車體地板剛接，其剛度不變，但質量大幅度增加，振動能量全部傳遞給車體地板，因此載人車體固有頻率大幅度降低.而將乘客考慮為多質量塊-彈簧-阻尼模型，車體與人體模型之間、人體各部分之間的彈簧和阻尼一定程度上會吸收乘客的部分振動能量，因此車體固有頻率相比于單質量塊模型而言有所增加.將乘客簡化為多質量塊-彈簧-阻尼的建模方法更接近于人體模型的實際情況，有利于進行乘客對車體振動模態影響的深入分析.

3 結論

本文建立了某高速動車組中間車未載人及載人狀態車體的有限元模型，通過計算獲得了整備未載人狀態和載人狀態車體的振動模態，得出以下結論：

(1)兩種整備載人狀態車體較整備狀態車體的四種典型振動模態頻率均有不同程度的降低，采用單質量塊模型對人體模型進行建模時，車體的四種典型模態頻率較未載人狀態降低幅度大，尤其是一階垂彎頻率，降低幅度達0.92 Hz.

(2)當采用多質量塊-彈簧-阻尼模型對人體進行簡化建模時，車體的四種典型模態頻率較未載人狀態降低幅度小，對于最為重要的一階垂彎頻率降低幅度僅為0.15 Hz，該種人體模型對車體的模態影響較小，基本可以忽略不計.

(3)將乘客簡化為多質量塊-彈簧-阻尼的建模方法更接近于人體模型的實際情況，有利于進行乘客對車體振動模態影響的深入分析.