具非線性對流項熱傳導方程的有限差分法
張繼紅,欒舒含,梁波
(大連交通大學 理學院,遼寧 大連 116028)
本文考慮如下帶有初邊值條件的具非線性對流項主部為熱傳導算子的對流擴散方程:
(1)
式中:x∈(a,b);t∈(0,T);指數p是參數.
許多物理現象,比如液體薄片在重力作用下的運動情況,流體在多孔介質中流動等都與方程(1)有關.Kamin[1]證明了不帶對流項的標準滲流方程源型解的存在唯一性;Brezis等[2]給出了具有吸收項的熱傳導方程測度初值問題解的存在性;盧國富證明了具非線性對流項主部為熱傳導算子的對流擴散方程的源型解[3].
近年來,對這類非線性偏微分方程的數值求解[4]也取得了很大進展,尤其是與Matlab軟件相結合,借助Matlab的數值計算和圖形處理技術[5],使得非線性偏微分方程解的意義更好理解.
本文主要研究具非線性對流項熱傳導方程的有限差分法實現,重點研究當參數p變化時,對方程的數值解會產生怎樣的影響.
1 有限差分法
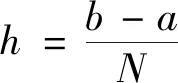
考慮內網點(xk,tn)處,原方程成立:
ut(xj,tn)-uxx(xj,tn)+|ux(xj,tn)|p=f(xj,tn)
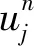
整理可得
(2)
與初邊值條件相應的差分方程為:
(3)
方程(2)與(3)聯立,即為與方程(1)相對應的差分方程.
2 數據實驗與結果分析
對具非線性對流項熱傳導方程(1),用差分格式(2)、(3)進行數值計算,區間設為[0,π],空間步長、時間步長分別取h=π/30、τ=0.001.
下面針對具體例子給出相應的數值實驗,重點研究參數p對差分解的影響情況.
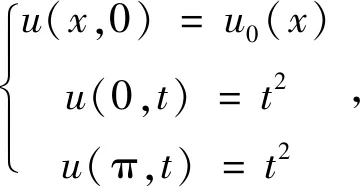
當參數p=1,時刻T=1時,可以得到相應的差分解,并與方程(1)的真實解u(x,t)=t2+sinx進行比較,得到的圖像分別如圖1~圖3所示.圖1為p=1,T=1時相應的數值解與真實解的對比圖,圖中可以看出數值解完全落在真實解的曲線上.圖2為p=1,時間t在[0,1]變化時的三維動態數值解模擬圖.圖3為p=1,時間t在[0,1]變化時的數值解與真實解絕對誤差圖.圖中可以看到絕對誤差不超過0.012,也就是說局部截斷誤差可以達到O(h2).
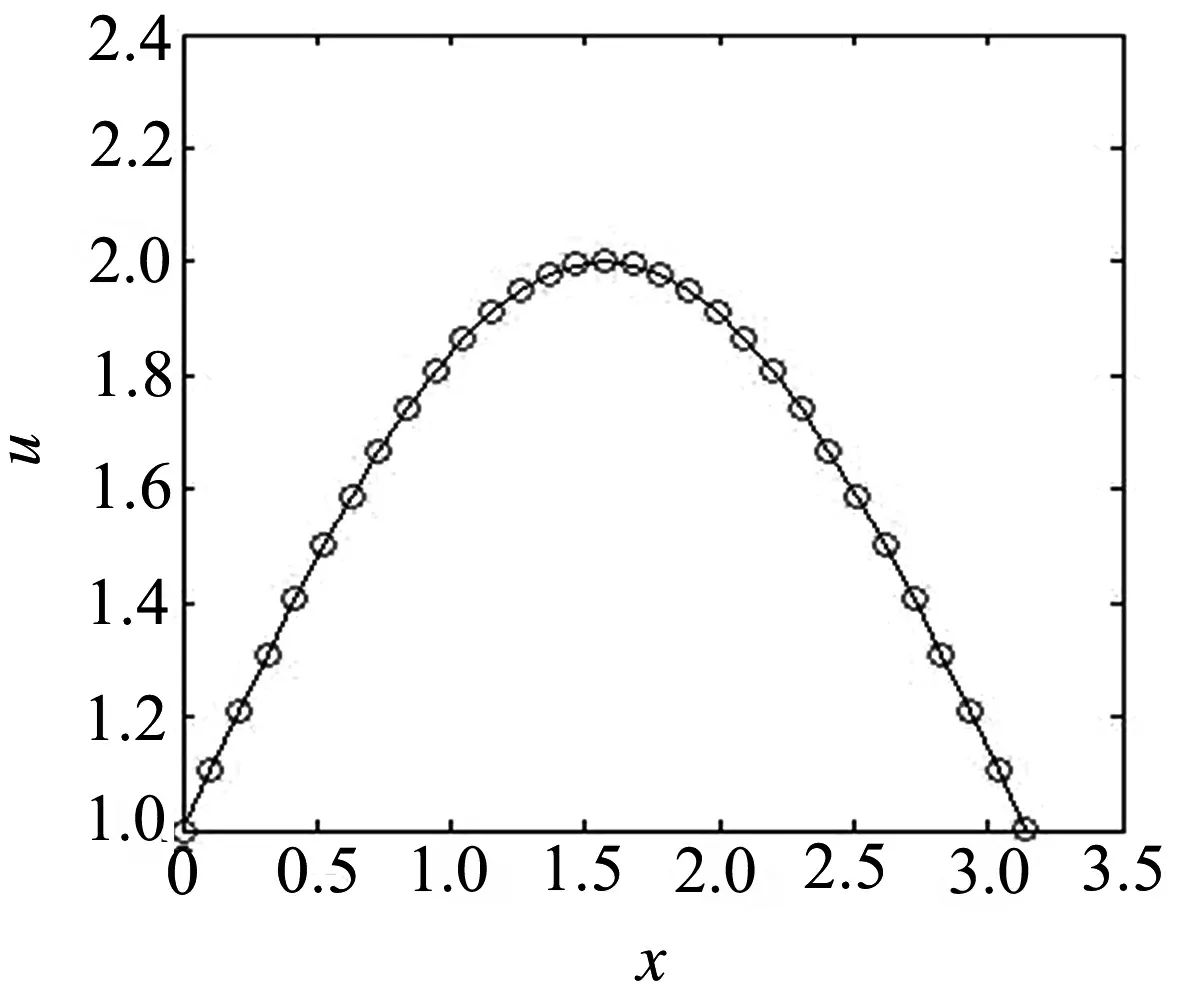
圖1 數值解與真實解對比圖
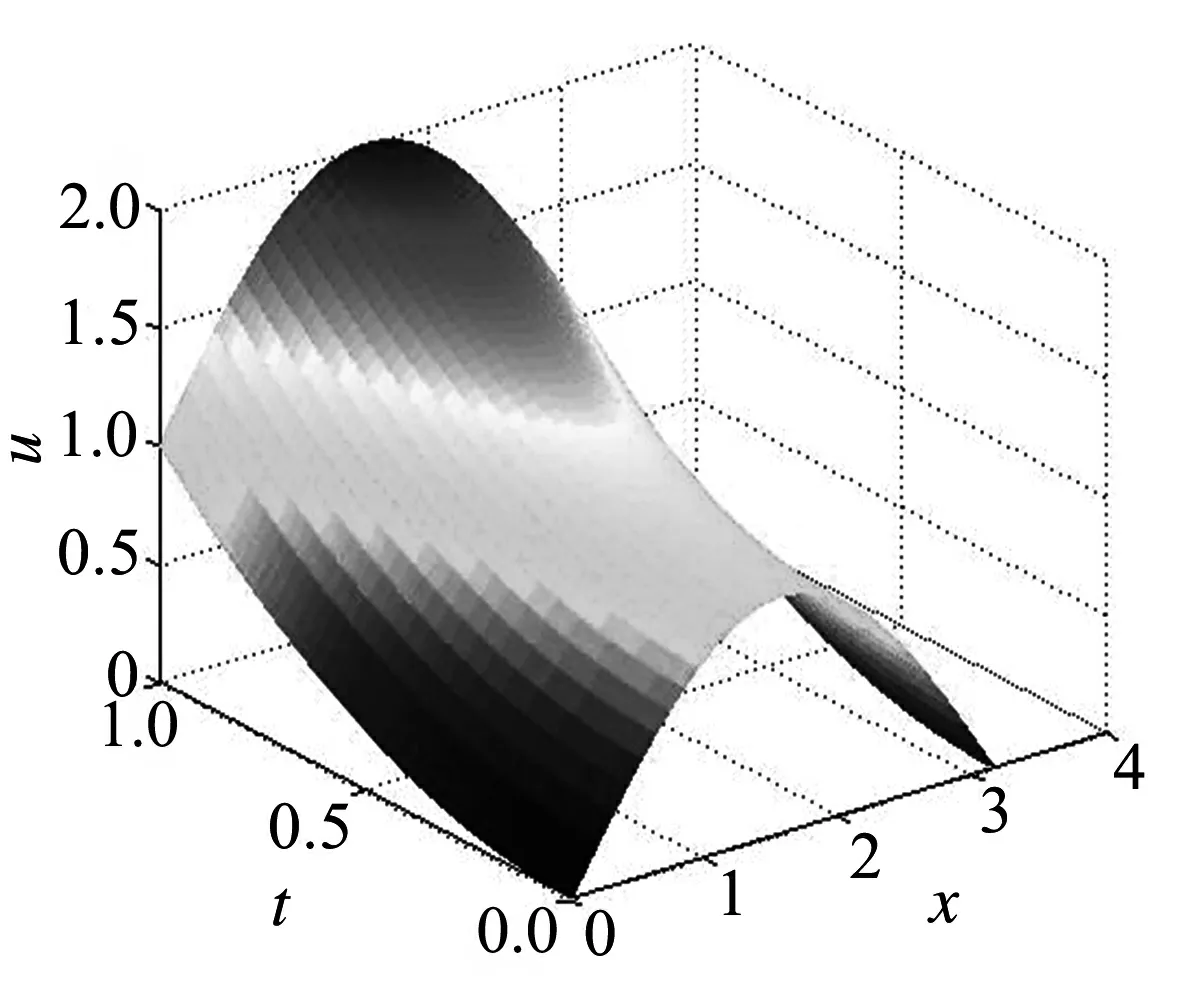
圖2 數值解三維圖像
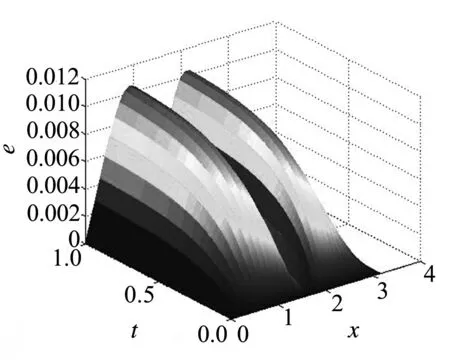
圖3 數值解與真實解絕對誤差三維圖
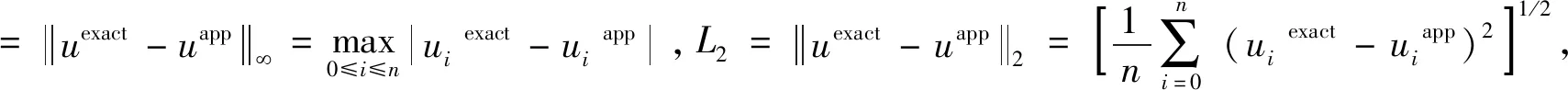
表1、表2分別給出了取不同參數p時,不同時刻T相應的誤差范數對比表.表1給出了p>1時,不同時刻T相應的誤差范數情況;表2給出了p<1時,不同時刻T相應的誤差范數情況.由表1可以看出,當p>1,L∞,L2數量級基本穩定在O(h2)時,當p發生變化,誤差并沒有明顯增長,且隨著時刻T的增加,誤差也沒有明顯增長,數值結果保持穩定.由表2可以看出,當p<1,L∞,L2數量級也基本穩定在O(h2)時,當p發生變化,誤差數量級沒有明顯增長,但是隨著參數p的變小,尤其是p=0.1時,誤差范數隨時間變化較大,兩種誤差范數都明顯增大,不能保持數值結果的穩定性.

表1 p>1時在不同時刻T相應的誤差范數對比表
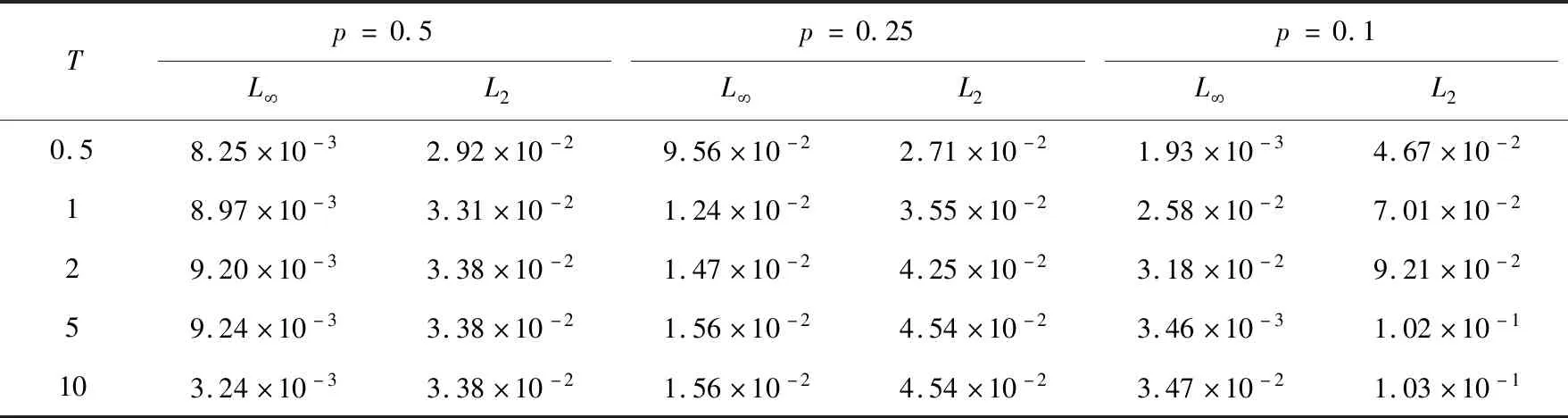
表2 p<1時在不同時刻T相應的誤差范數對比表
3 結論
具非線性對流項熱傳導方程具有一定的研究意義,對其進行數值計算可以更加方便地研究和解決實際問題.本文引入了具非線性對流項熱傳導方程的有限差分法,通過具體算例,探討了當參數p發生變化時,相應的差分解是否會發生改變的情況.當p>1時,對差分解的影響不大,并且當計算過程長時間進行時,數值結果依然能保持穩定;當p<1,計算結果也沒有發生明顯變化,但是參數p取得過小,可能會使數值結果不穩定.

