非線性三階方程三點邊值問題解的存在性和唯一性

王國燦

(大連交通大學(xué) 理學(xué)院，遼寧 大連 116028)

三階非線性微分方程的三點邊值問題在常微分方程理論研究中有一定的積極意義，同時在工程物理學(xué)中有很多應(yīng)用[1-4]，但工作重點主要是分析特殊的非線性方程與線性邊值問題，而且對于解的唯一性的研究并不多.本文利用上下解理論[5-8]，討論以下一般的三階非線性三點邊值問題:

x?=f(t,x,x′,x″)

(1)

(2)

本文將在普通意義下研究問題(1)與(2)的解的存在性、唯一性.

1 輔助引理

下面考慮一類二階積分微分方程的非線性邊值問題

u″=f(t,Tu,u,u′)

(3)

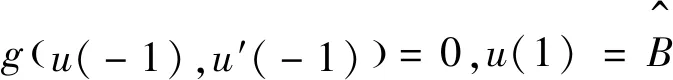
(4)

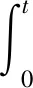
定義1 如果給定的函數(shù)β(t)和α(t)∈C2[-1,1]，在[-1,1]上使得α(t)≤β(t)，β″(t)≤f(t,[Tβ](t),β(t),β′(t))，α″(t)≥f(t,[Tα](t),α(t),α′(t))，則稱β(t)和α(t)為方程(3)的上解與下解.

引理1如果滿足下列條件：

(1)引理1中的(1)，(2)成立；

(2)g(ξ,η)∈C(R2)，且g(ξ,η)對固定的ξ關(guān)于η單調(diào)不減；

(3)方程(3)有上解β(t)和下解α(t)，且

g(α(-1),α′(-1))≥0，

g(β(-1),β′(-1))≤0，

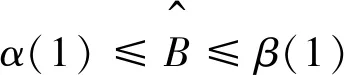
則邊值問題(3)、(4)有解u(t)，使得α(t)≤u(t)≤β(t)，-1≤t≤1.

證明：利用迭代法構(gòu)造序列及一致有界同等連續(xù)原理，可得定理為真.

引理2如果滿足下列條件

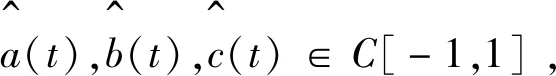
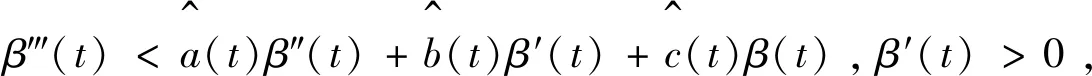
則邊值問題

(5)

ay′(-1)+by″(-1)=0,

y(0)=0,y′(1)=0

(6)

只有零解.

證明：利用反證法構(gòu)造與結(jié)論矛盾的結(jié)果，可知引理成立.

2 主要結(jié)果

下面將討論邊值問題(1)、(2)解的存在性與唯一性.

定義2 如果存在函數(shù)β(t)和α(t)∈C3[-1,1]，使得當(dāng)-1≤t≤1時，α′(t)≤β′(t)，β?(t)≤f(t,β(t),β′(t),β″(t))，α?(t)≥f(t,α(t),α′(t),α″(t))，且當(dāng)-1≤t≤0時，

β(t)≤α(t)，當(dāng)0≤t≤1時，α(t)≤β(t)，則稱β(t)和α(t)為方程(1)的上下解.

如果函數(shù)f(t,x,x′,x″)滿足下列兩個條件之一，則稱方程(1)具有三階Nagumo條件：

(a)對任何的正數(shù)N，存在正函數(shù)h=h(N)，使得(t,x,x′,x″)∈[0,1]×[-N,N]×R2成立時|f(t,x,x′,x″)|≤hΦr1(|x′|)Φr2(|x″|)，其中0≤r1≤1，r2>0，r1+r2≤3，且Φr(l)=max{1,lr},r>0，0≤l≤+∞；

(b)對任何的(t,x,x′)∈[0,1]×R2使得f(t,x,x′,x″)=O(|x″)|2)，|x″|→∞.

定理1如果下列條件滿足

(1)f(t,x,x′,x″)∈C([-1,1]×R3)，符合Nagumo要求，且當(dāng)-1≤t≤0時，關(guān)于x單調(diào)不減；當(dāng)0≤t≤1時，關(guān)于x單調(diào)不增；

(2)引理2中的(2)成立；

(3)方程(1)存在上下解β(t)和α(t)，且

則邊值問題(1)，(2)存在解x(t)∈C3[-1,1]，不等式β(t)≤x(t)≤α(t),-1≤t≤0，α(t)≤x(t)≤β(t),0≤t≤1成立.

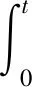
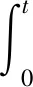
(1)′

g(u(-1),u′(-1))=0,u(1)=B

(2)′

又由x(t)構(gòu)造得到

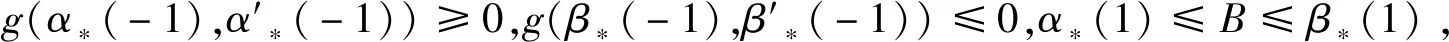
定理2如果下列條件滿足

(1)定理1中的(1)，(2)成立;

(2)存在函數(shù)β(t)∈C3[-1,1]，當(dāng)-1≤t≤1時,0<β′(t),0<β″(t)，β?(t)≤fx″(t,x,x′,x″)β″(t)+fx′(t,x,x′,x″)β′(t)+fx(t,x,x′,x″)β(t)，且當(dāng)-1≤t≤0時，β(t)≤0，當(dāng)0≤t≤1時，0≤β(t)，β(0)=0；

(3)對任意ξ,η∈(-∞,+∞)，滿足gξ(ξ,η)β′(-1)+gη(ξ,η)β″(-1)<0；

則邊值問題(1)、(2)有唯一解.

證明：利用反證法.如果邊值問題(1)、(2)存在兩個相異的解x1(t)，x2(t)，記y(t)=x2(t)-x1(t)，則y(t)應(yīng)滿足下述邊值

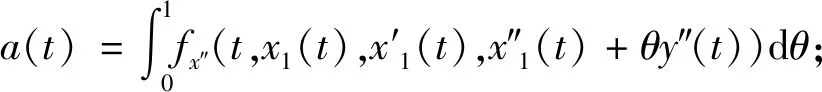
由條件(1)知，a(t),b(t),c(t)于-1≤t≤1上連續(xù)，且c(t)≥0,-1≤t≤0，c(t)≤0,