高速列車頭型的減阻降噪多目標優化設計

季玲，劉海東，陳秉智

(大連交通大學 機車車輛工程學院，遼寧 大連 116028)

隨著列車運行速度的提高，空氣阻力、空氣升力和空氣噪聲等空氣動力學問題的影響逐漸加劇[1-2].當列車速度達到300 km/h時，空氣阻力占總阻力的75%，增加了列車能耗；空氣升力降低了列車運行的安全性，正升力過大，輪軌間作用力嚴重降低時甚至導致列車脫軌；負升力過大，輪軌間磨耗增加；空氣噪聲成為主要噪聲源，降低了乘坐舒適性[3-8].列車空氣阻力、空氣升力和列車表面噪聲源聲功率與頭型幾何曲面有密切關系，故列車頭型的優化設計成為改善高速列車的噪聲性能和氣動性能的主要措施[9-10].Sun等[11]和姚拴寶等[12]以空氣阻力為目標，分別采用MOGA-Ⅱ和改進的蟻群算法對列車頭型進行優化設計.李明等[13]以空氣阻力和空氣升力為目標，分別采用伴隨方法和NSGA-Ⅱ算法，對列車頭型進行多目標優化.Krajnovic[14]以橫風穩定性和空氣阻力為目標，研究3種近似模型對列車優化設計的影響，結果表明：徑向基神經網絡和多項式函數的組合模型效果較好.劉加利等[15]對列車頭型進行多目標優化設計，降低列車的空氣阻力和偶極子噪聲源.于夢閣等[16]以空氣阻力和輪重減載率為目標，基于Kriging近似模型對列車頭型進行多目標優化，優化后列車的空氣阻力減小3.27%，輪重減載率減小1.44%.

以上研究工作專注于優化高速列車頭型的氣動性能，較少同時考慮列車的噪聲性能和氣動性能，并且大多數氣動頭型優化研究僅僅針對一個或兩個氣動優化目標進行研究，得到的優化頭型效果有限.此外，對高速列車頭型進行優化設計時，每次優化迭代都需要對整車模型進行參數化幾何建模、網格劃分和空氣動力學計算，優化設計時間長.因此，本文采用Isight軟件集成Sculptor和Fluent模塊，以高速列車的空氣阻力、空氣升力和列車表面噪聲源聲功率為優化目標，運用ASD技術和響應面近似模型，采用NSGA-Ⅱ算法對高速列車頭型進行多目標自動優化設計.

1 優化設計流程

本文設計了如下的優化流程(圖1)，運用ASD技術快速建立列車網格模型，經空氣動力學計算得到優化目標值，構建設計變量關于優化目標的響應面近似模型，并采用NSGA-Ⅱ算法進行多目標優化設計.

圖1 優化設計流程

2 高速列車空氣動力學模型

2.1 控制方程

本文高速列車運行時馬赫數小于0.3，可以忽略空氣密度變化對流場的影響[17].因此，采用三維不可壓縮非定常方程進行模擬：

連續方程：

(1)

N-S方程：

(2)

式中：ui、uj為流場速度；xi、xj為坐標分量；ρ為空氣密度；p為熱力學壓強；μ為空氣動力黏度.

高速列車周圍流場采用k-ε模型模擬.

湍流黏性系數μt為：

(3)

湍流動能k方程為：

(4)

湍流耗散率ε方程為：

(5)

式(3)～式(5)中：Cu為湍流常數，取值為0.09；c1、c2、σk、σε為經驗常數，取值分別為1.47、192、1.0、1.33.

Proudman方程利用Lighthill理論模擬各向同性湍流運動聲功率：

(6)

式中：α為模型常量；ρ為空氣密度；u為湍流速度；l為湍流尺度；c0為聲速.

聲功率級Lp為：

LP=10 lg(PA/Pr)

(7)

式中：Pr為參考聲功率;Pr=10-12W/m3.

聲功率可以估計單位體積或面積的局部噪聲.

2.2 數值模型

本文計算模型為三節編組列車(頭車+中間車+尾車)，列車運行速度為350 km/h.對高速列車車頭表面網格細化，最大尺寸為50 mm，其他部位網格不超過100 mm.流場采用四面體網格離散，網格最大尺寸為2 400 mm.流場左側為速度入口邊界，右側為壓力出口邊界.地面為運動壁面，移動速度與入口速度相同，模擬地面效應.在高速列車穩態計算的基礎上，利用寬頻噪聲模塊計算列車表面噪聲源分布.模型計算區域見圖2，列車流線型頭型網格模型見圖3.

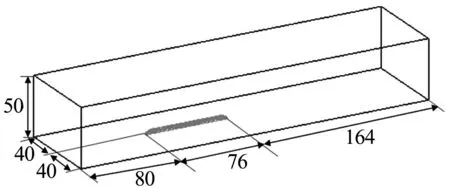
圖2 模型計算區域

(a) 列車頭型網格

3 網格驅動變形技術

3.1 ASD技術

本文采用基于Sculptor軟件的網格驅動變形技術(Arbitrary Shape Deformation，ASD)在網格處建立控制體，一個ASD控制體包括多個控制點及控制點間連線.控制點移動，相鄰區域網格隨之移動，實現網格變形.網格移動滿足C1連續，保證網格光滑變形.網格驅動變形技術為復雜模型的外形優化供了可行性.

3.2 定義設計變量

選取高速列車模型的控制點，控制列車車頭形狀.在車頭頂部選取5個設計變量(dy1、dy2、dy3、dy4和dy5)，控制車頭沿垂向變形；在車頭兩側選取設計變量dz，控制車頭沿橫向變形；在車頭前部選取設計變量dx，控制車頭沿縱向變形.高速列車頭車和尾車控制點對稱布置圖，控制點布置見圖4.根據工程經驗，設計變量的取值范圍見表1.

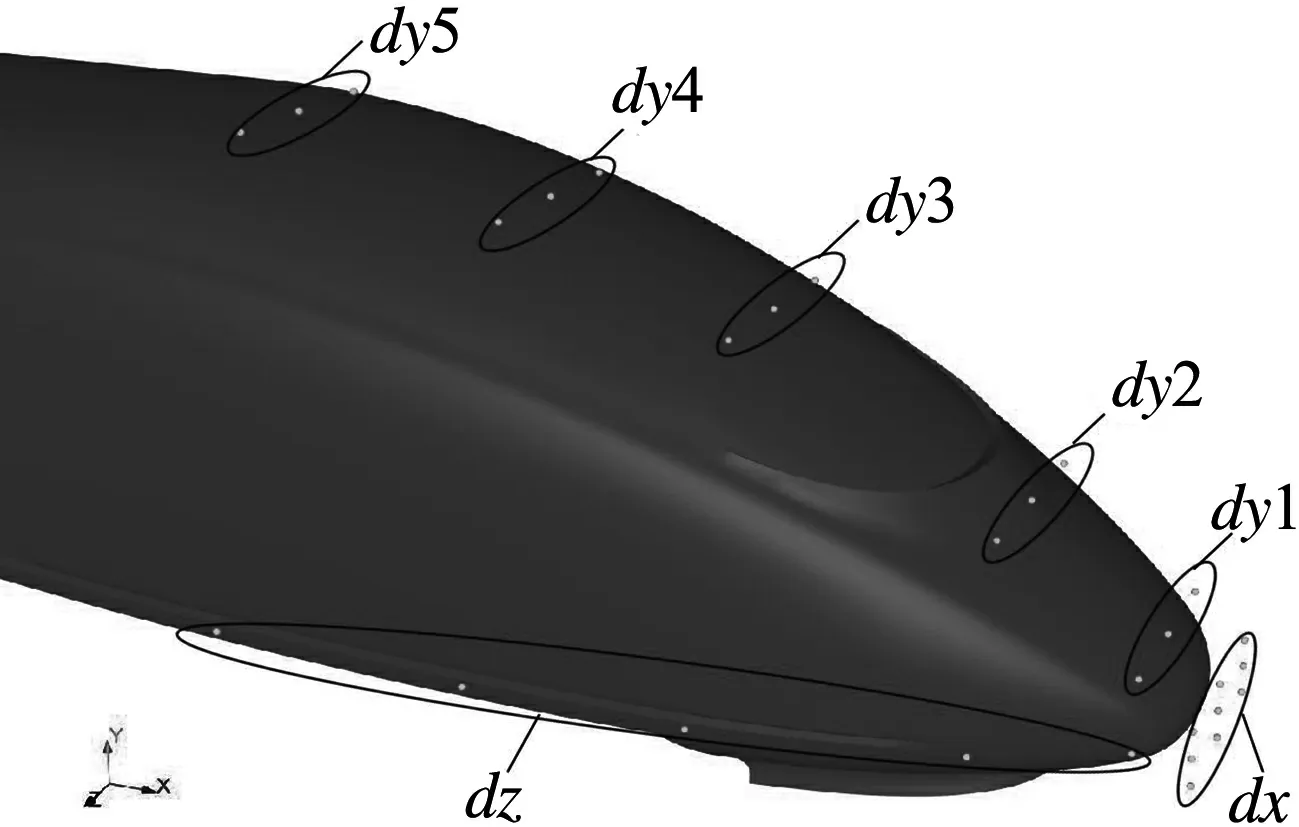
(b) 流場縱向對稱面網格圖4 控制點布置

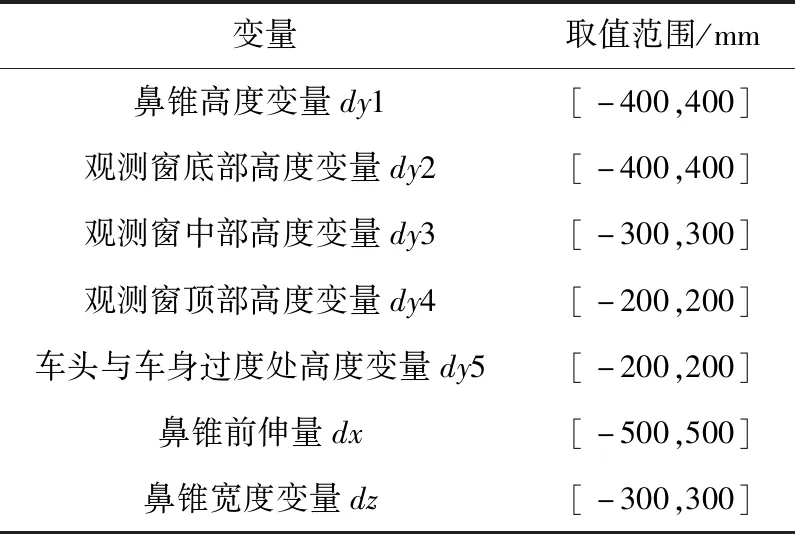
表1 設計變量取值范圍

4 多目標優化計算及結果分析

4.1 多目標問題描述

本文以高速列車的空氣阻力絕對值最小化、空氣升力絕對值最小化和列車表面噪聲源聲功率最小化為優化目標，進行多目標優化設計.

4.2 構造響應面近似模型

采用最優拉丁超立方采樣法選取200組樣本，分別構建列車空氣阻力、空氣升力和列車表面噪聲源聲功率的四次多項式響應面近似模型.隨機選取10個樣本點進行誤差分析，檢驗近似模型精度，分析指標包括：均值(Average)、最大值(Maximum)、均方根(Root Mean Square)、相關系數(R-Squared).列車空氣阻力、空氣升力和列車表面噪聲源聲功率的預測值與真實值對比見圖5.列車空氣阻力、空氣升力和列車表面噪聲源聲功率的預測值與真實值基本接近.表2給出了近似模型的誤差分析結果，列車空氣阻力、空氣升力和列車表面噪聲源聲功率的誤差均滿足相應的誤差分析指標要求.

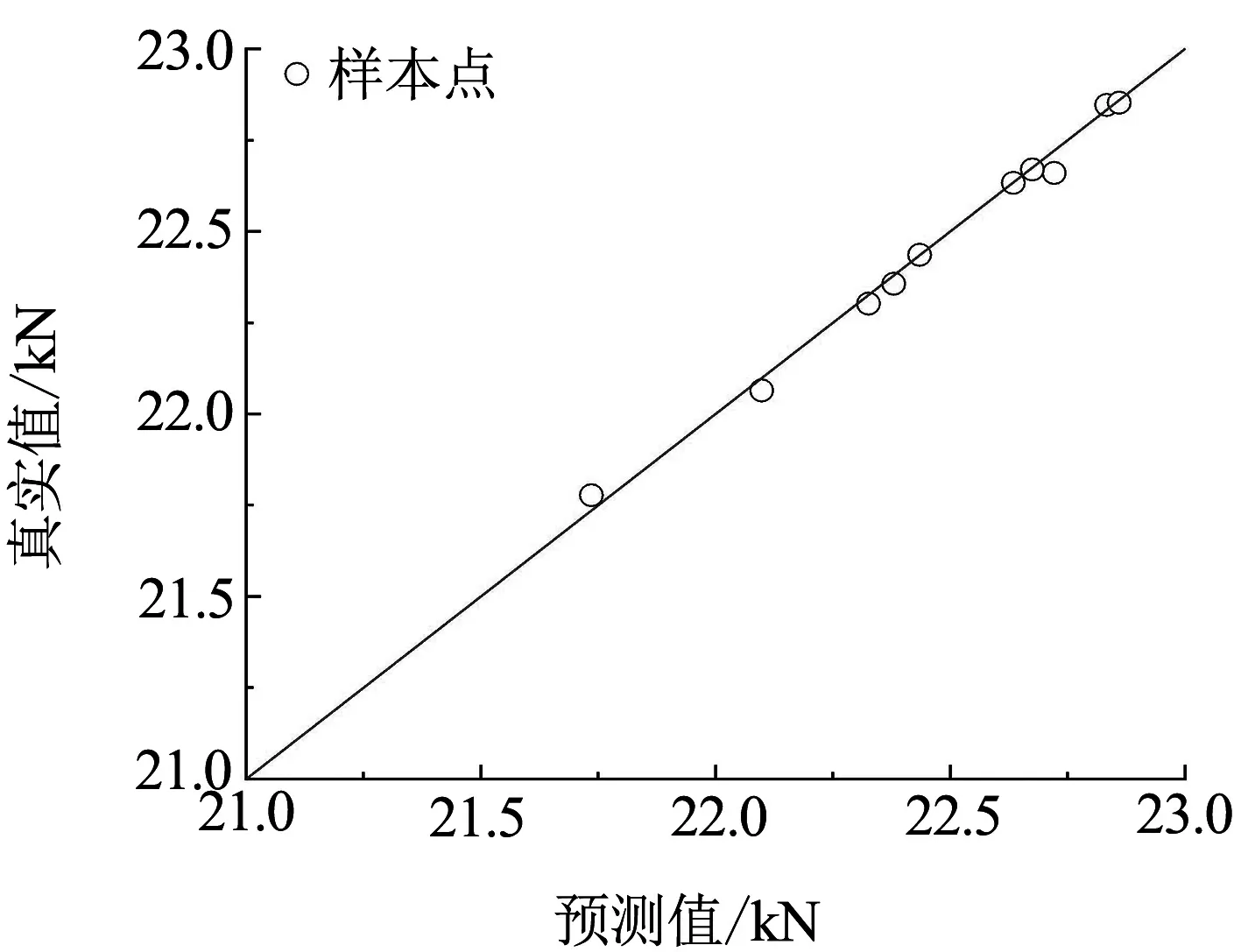
(a) 空氣阻力對比

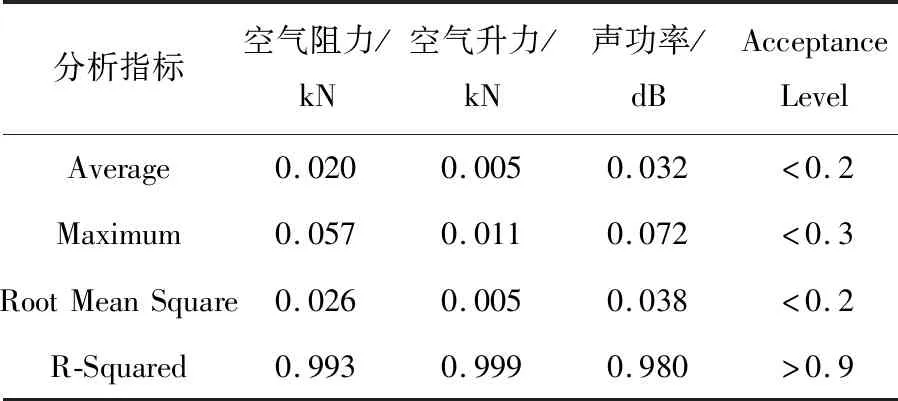
表2 近似模型誤差分析

4.3 優化結果分析

本文基于列車空氣阻力、空氣升力和列車表面噪聲源聲功率的四次多項式響應面近似模型，采用第二代非劣排序遺傳算法NSGA-Ⅱ對高速列車頭型進行多目標優化設計.NSGA-Ⅱ算法的種群規模設為24，進化代數為24代，交叉概率為0.9.將多個目標函數合并為單目標時，需指定各目標函數的縮放因子和權重系數.本文的三個優化目標數量級相差較大，為得到均衡的優化結果，目標函數的縮放因子和權重系數見表3.

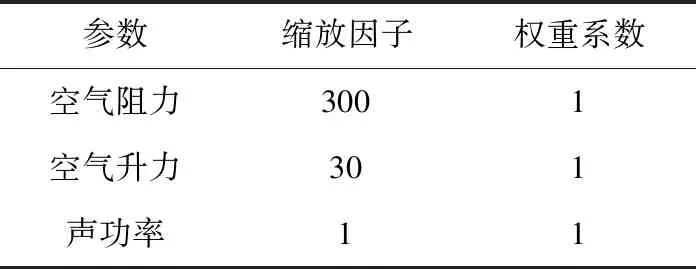
表3 縮放因子和權重系數

優化目標的Pareto前沿解集見圖6.表4給出了從Pareto前沿解集中選取的新頭型P1～P5和優化前原頭型P0的氣動性能和噪聲性能對比.新頭型P1為空氣阻力最小的頭型；新頭型P2為空氣升力最小的頭型，同時新頭型P2為Pareto最優解；新頭型P5為列車表面噪聲源聲功率最小的頭型.選取最優新頭型時，應確保新頭型的空氣阻力、空氣升力和列車表面噪聲源聲功率都小于原列車的初始值，故不考慮新頭型P5.因為新頭型P1～P4的空氣阻力和列車表面噪聲源聲功率變化比例較小，選擇空氣升力最小的新頭型P2作為優化后的模型進行分析.優化后，列車空氣阻力減小5.20%，空氣升力減小36.68%，列車表面噪聲源聲功率減小2.11%，列車的氣動性能和噪聲性能有所改善.

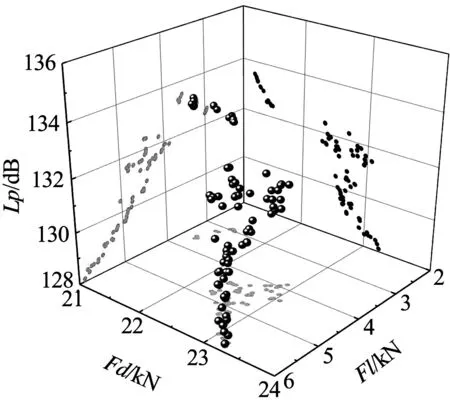
圖6 優化目標的Pareto前沿解集

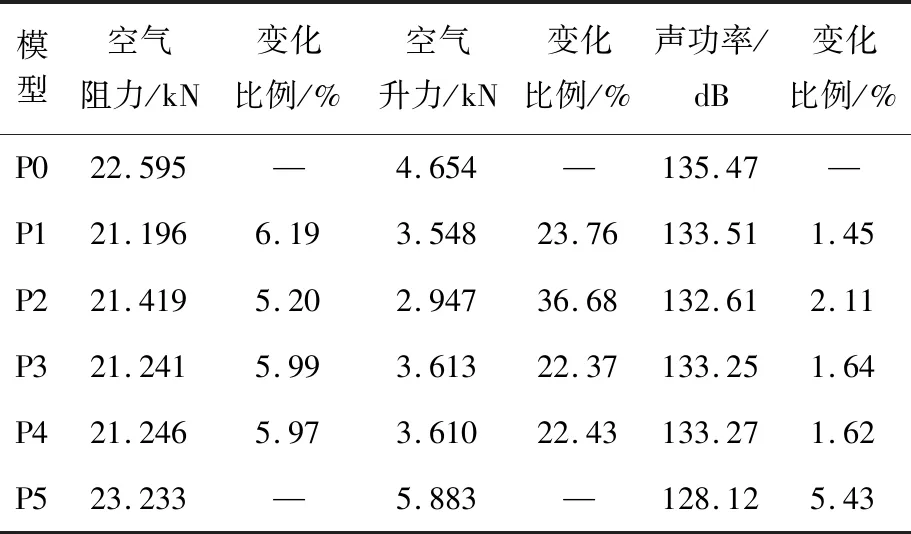
表4 優化前后模型的結果對比

對優化后的列車頭型進行空氣動力學計算驗證，結果見表5.列車空氣阻力的相對誤差為0.06%，空氣升力的相對誤差為2.26%，列車表面噪聲源聲功率級的相對誤差為0.54%，優化結果與空氣動力學仿真計算結果的誤差在允許范圍.

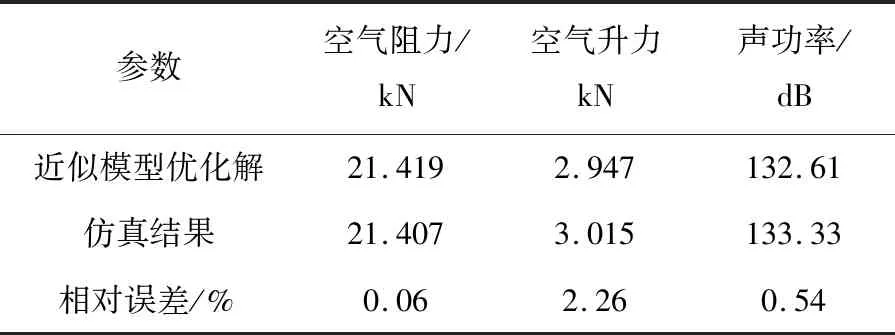
表5 優化結果驗證

表6給出了當高速列車速度為300 km/h、400 km/h和500 km/h時優化前、后的列車氣動性能和噪聲性能對比.相比于原頭型，優化后的列車頭型在不同速度下的空氣阻力、空氣升力和列車表面噪聲源聲功率都減小，列車的氣動性能和噪聲性能提高，有較好的優化效果.隨著列車速度提高，列車的空氣阻力和空氣升力的變化比例增大，列車表面噪聲源聲功率的變化比例減小.

圖7給出了優化前、后列車頭型的變量變化幅值.圖8給出了優化前、后列車的流線型頭型對比，虛線為優化前的原頭型，實線為優化后的列車頭型.與原頭型相比，優化后頭型的鼻錐前伸量增大，鼻錐寬度減小，鼻錐高度增高，觀察窗高度增高且內凹，車頭與車身過渡處高度降低.

表6 不同速度下優化前后模型的結果對比

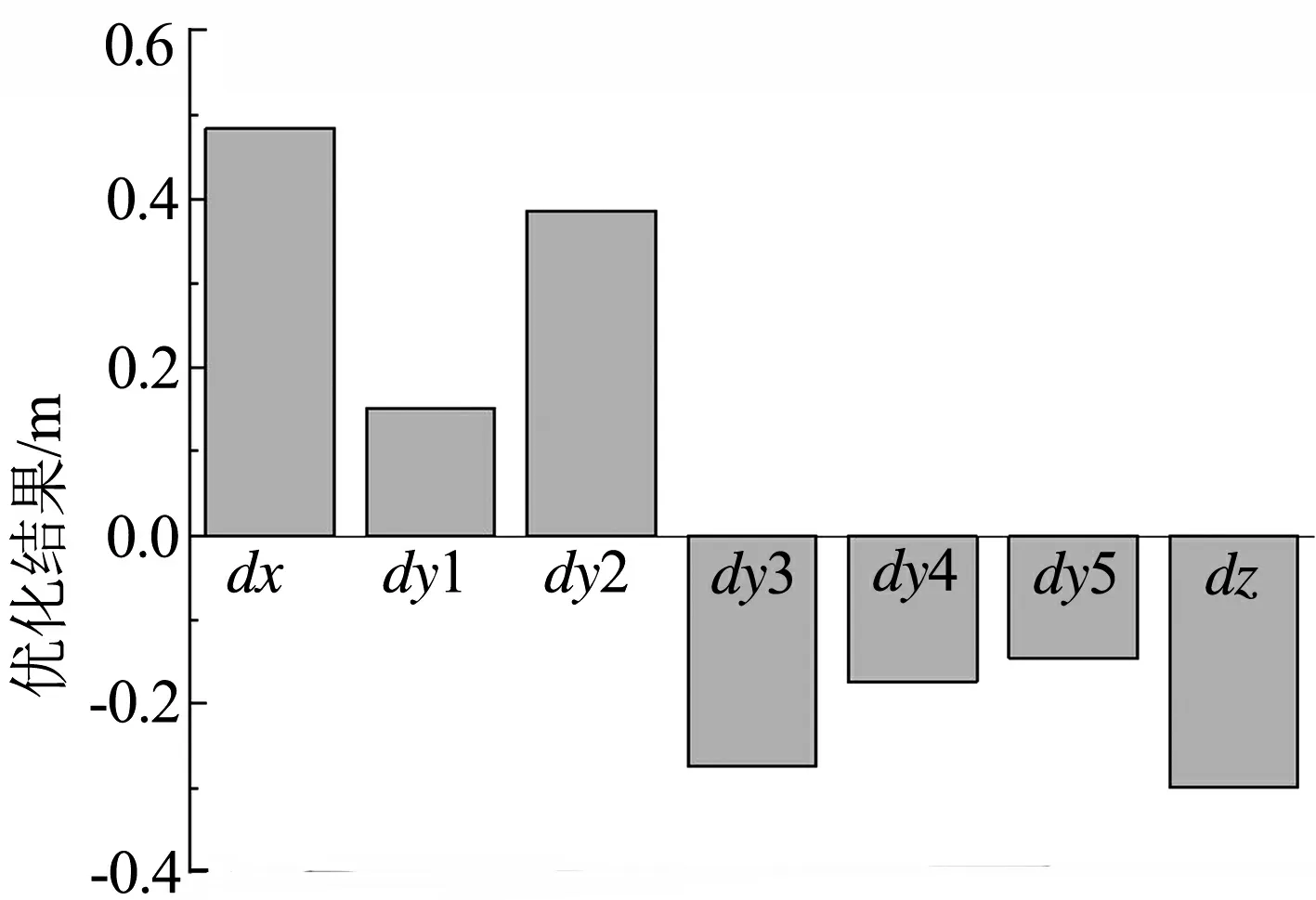
圖7 變量變化幅值

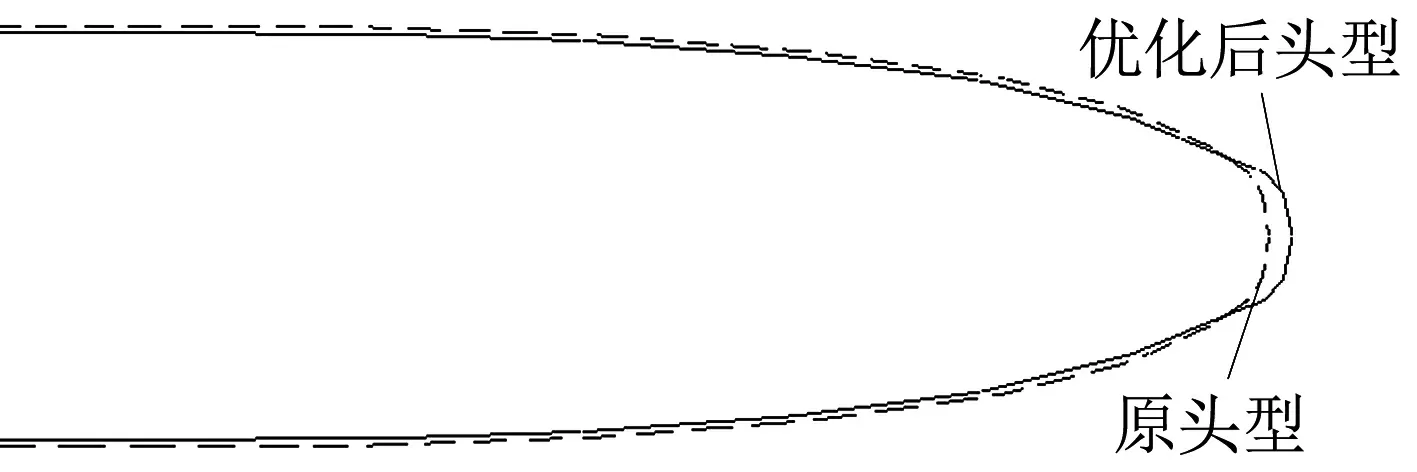
(a) 垂向視圖

圖9給出了優化前、后列車頭型表面的壓力分布，優化后高速列車頭車的正壓區比優化前原頭型頭車的正壓區小，正阻力減小；尾車的正壓區比原頭型尾車的正壓區大，負阻力增大，故優化后列車的空氣阻力降低.優化后尾車鼻錐頂部正壓區比原頭型尾車的正壓區大，故優化后列車的空氣升力降低.優化后列車頭車的正壓區比原頭型頭車的正壓區分布更均勻，氣流擾動程度降低，故優化后列車表面噪聲源聲功率降低.

(a) 頭車表面壓力分布圖9 優化前、后列車頭型表面壓力分布

5 結論

(1)本文以高速列車空氣阻力、空氣升力和列車表面噪聲源聲功率為優化目標，運用ASD技術和響應面近似模型，采用遺傳算法NSGA-Ⅱ，對高速列車頭型進行多目標自動優化設計，縮短高速列車流線型頭型的優化時間，提高優化設計效率.

(2)相比于原頭型，優化后的高速列車頭型鼻錐前伸量增大，鼻錐寬度減小，鼻錐高度略增高，觀察窗高度增高且內凹，車頭與車身過渡處高度降低；優化后的列車空氣阻力減小5.20%，空氣升力值減小36.68%，列車表面噪聲源聲功率減小2.11%，列車的氣動性能和噪聲性能提高，且在不同運行速度下，都得到較好優化效果，具有一定工程參考價值.