風光不與四時同
——我的數學教學四景

閻靖崢 (西安交通大學蘇州附屬初級中學 215000)

蘇州園林早已聞名世界，正所謂“江南園林甲天下，蘇州園林甲江南”．在歷史的長河里，坐落在姑蘇古城內的一座座園林熠熠生輝，拙政園、獅子林、留園等都以自己獨特的方式散發著屬于姑蘇城的秀色可餐之景．走近造園大師，我們會驚喜地發現，他們的造景方式大致可以分為：引景—對景—框景—漏景等手法.反觀自己的數學教學過程，或許也能夠模仿大師們的技藝，努力讓自己的教學形成更高效的精品課堂，尋找屬于我的數學教學四景．

1 巧用“引景”，精準定位

在美麗的蘇州園林里，景色多樣，橫看成詩側成畫．其實，在造園的時候，園林工匠們早已有意識地為游人的游覽設定了特定的路線方式，引導他們更順暢、更直觀地感受園林之美，如圖1的藤蘿架、圖2的鵝卵石小道、圖3的別致長廊．游客們可以在特定的路線上感受到園林的婀娜多姿．

圖1 圖2 圖3

在數學復習階段，很多教師認真地為學生將每一份試卷中的題目逐一進行詳細講解，生怕遺漏了任何一個知識點．這樣做，在彌足珍貴的復習時間里顯得效率比較低下，而且學生一節課的注意力集中時間也是有限的，既浪費了時間，也很難做到重點突出．我們不妨適當“引景”，在課前下足功夫，將學生的錯誤進行統計，挑選一些共性的問題進行集中教授，同時更應該走近學生，了解學生錯誤的真實原因，而非以我們自己的觀點去認定學生“不該錯”“這么簡單還在錯”等．

例1

將14 400精確到千位約等于

．

解析 數14 400的千位為第一個“4”，故答案為1.4萬或者14千或者1.4×10．

這是一道很簡單的問題，但是一大部分學生在解答時候，給出的答案卻是14 000．教師們可能會感到不可思議：為什么這么簡單的問題學生都不會呢？筆者所在的班級此題錯誤率高達56%，隨機采訪了幾位錯誤的學生，請他們分析自己錯誤的原因，好幾個學生都說自己沒有想到后面的幾個零不可以加上去，不假思索地寫出了錯誤答案．通過問題的分析，我們不難發現，學生做錯的根本原因在于基本概念的理解偏差．所謂“近似值的精確度”，數字的最后一位數所在的真實數位即為該數的精確度．理解了基本概念后，學生可以很快發現自己寫的答案14 000的最后一個數“0”是在個位上的，并不滿足題目的要求．

例2

如圖4，某縣正在創建全國衛生城市，打算建立污水處理系統，計劃在道路

l

，

l

兩旁建立一個污水處理站

M

，使點

M

到兩條道路

l

，

l

的距離相等，且

AM

=

BM

．(不寫作法，保留作圖痕跡)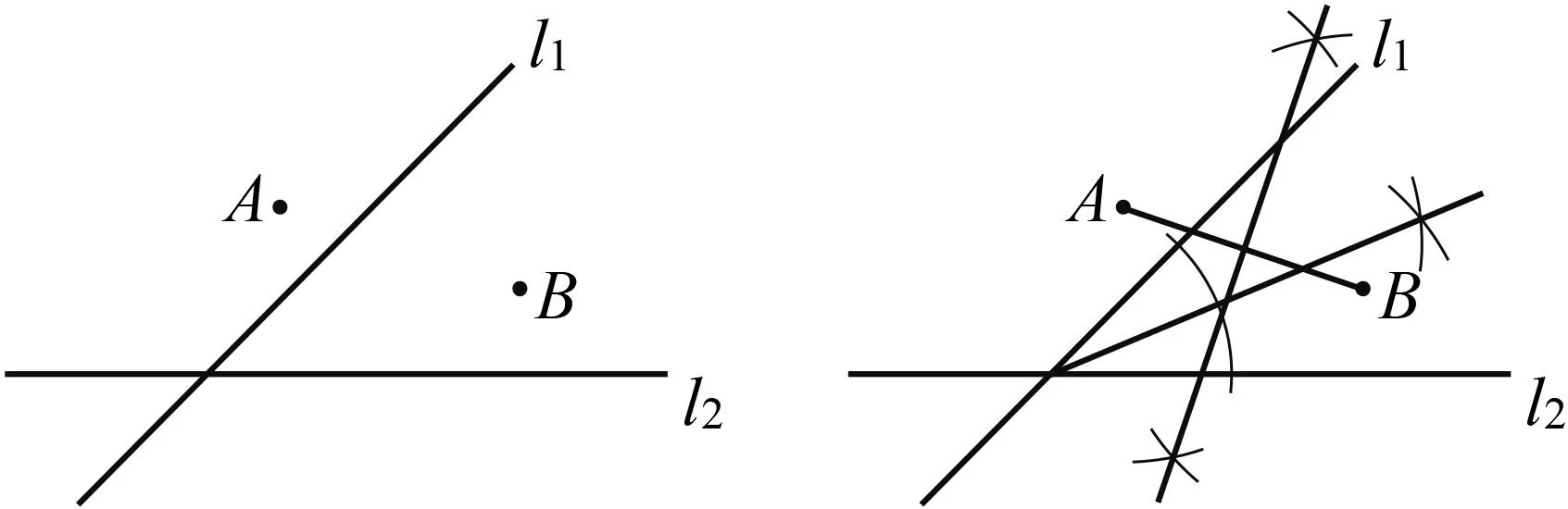

圖4 圖5

解析 由

AM

=

BM

可知，連結線段

AB

，作線段

AB

的垂直平分線；由“點

M

到兩條道路

l

，

l

的距離相等”可知，作

l

，

l

兩條直線夾角的平分線，所作這兩條線的交點即為所求．解題時，很少有學生能夠將圖象畫完整，大部分學生都呈現了如圖5的角平分線畫法，遺漏了另一種情況．分析后發現，學生都在采用經驗解題，條件反射般地畫出了

l

，

l

兩條直線所夾銳角的角平分線，卻遺漏了所夾鈍角的角平分線．我們可以在掌握這一訊息后引導學生做題的時候全方位思考，理解直線的夾角有兩個．

以上兩個實例都是教師在復習課上精準把握班級學情，準確定位應講該講的題目，同時能夠了解學生的真實錯因，從而在課堂將思維重現，學生可以在教師引的“景”上重新走一遍，發現自己的思維漏洞，領略到別樣的精彩，有助于學生數學抽象核心素養的形成．

2 妙用“對景”，舉一反三

蘇州園林在景致坐落上特別講究景觀的“對”，即通過軸線去確定景觀的位置，從而產生秩序、嚴肅或崇高的人體感受．蘇州園林的景觀從不講究對稱，每一處亭臺樓閣、每一個石凳小橋都與園中的草木互相配合布置，別有洞天，各具特色，少了些刻板，多了些靈動．例如，圖6的視角，園林的設計師巧妙地借了北寺塔的景，既解決了園林空間有限的問題，還節省了大量的經費；圖7的視角，白色的四葉門與后面的假山融為一體，儼然是一副美麗的風景畫；圖8的視角下，亭臺、水面、假山、荷花呈現一字排開的狀態，給人一種和諧的美感．

圖6 圖7 圖8

在復習階段，題型眾多，學生很容易就會陷入題海之中，教師在教學的過程中應當時刻注意題目的變化，引導學生多思考，切忌一味盲目地刷題．在解例3的時候，大部分學生做出來的答案都是38°，屬于猜測的范疇．而這個題目的解決關鍵在于題干中不經意的一句話“點

A

，

B

恰好重合于點

P

處”，透過表象看本質，這個條件是在引導學生使用

AD

，

PD

，

BD

邊相等，從而從角的關系出發，落腳點卻在邊的關系上．解決例3之后，可以轉換視角，讓學生在熟悉的背景下再進行線段長度的計算.通過例3、例4兩個題目，可以讓學生養成分析問題、類比的數學學習方式，有助于學生邏輯推理核心素養的形成．

例3

如圖9，在△

ABC

中，∠

C

=90°，∠

A

=38°，

D

,

E

分別為

AB

,

AC

上一點，將△

BCD

,△

ADE

分別沿

CD

,

DE

翻折，點

A

,

B

恰好重合于點

P

處，則∠

ACP

=

．

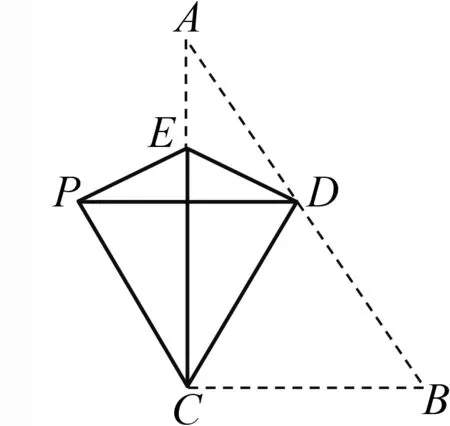
圖9

解析 由“△

BCD

,△

ADE

分別沿

CD

，

DE

翻折，點

A

,

B

恰好重合于點

P

處”可知

AD

=

PD

=

BD

，故

CD

是直角△

ABC

的斜邊上的中線，可得

CD

=

BD

，故∠

B

=∠

BCD

=∠

PCD

=52°，所以∠

ACD

=90°-∠

BCD

=90°-52°=38°，于是∠

ACP

=∠

PCD

-∠

ACD

=52°-38°=14°．

例4

如圖10，在Rt△

ABC

中，點

D

為斜邊

AB

的中點，連結

CD

，將△

DBC

沿

CD

翻折，使點

B

落在點

E

處，點

F

為直角邊

AC

上一點，連結

DF

，將△

ADF

沿

DF

翻折，使點

A

與點

E

重合，求折痕

DF

的長．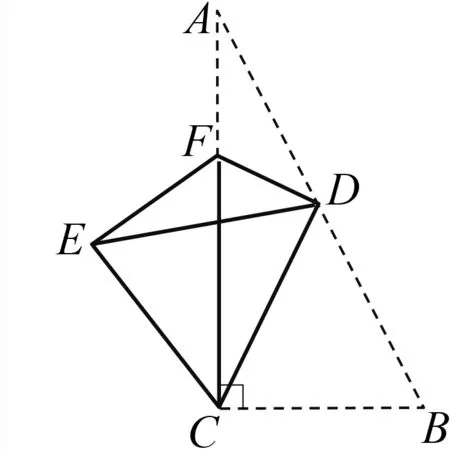

圖10

解析 由“點

B

落在點

E

處”“點

A

與點

E

重合”可知，

CD

是直角△

ABC

的斜邊上的中線．設

AF

=

EF

=

x

，在Rt△

CEF

中，利用勾股定理求出

x

，再在Rt△

DCF

中，求出

DF

即可．

俗話說“上山容易下山難”，而幾何的學習本身就是一個“逆推”思考和“順寫”答題的過程．如果在教學的過程中，教師能夠將題目進行巧妙的設計，使得學生能夠從正反兩個維度去理解題目，必定可以贏得學生的拍手稱贊，幫助他們真正意義上做到舉一反三、觸類旁通，也一定會鑄就一道靚麗的教學風景線．例5、例6也是這樣的“一對”.

例5

如圖11，在Rt△

ABC

中，∠

C

=90°，點

P

為

AC

邊上的一點，延長

BP

至點

D

，使得

AD

=

AP

，當

AD

⊥

AB

時，過點

D

作

DE

⊥

AC

于

E

．

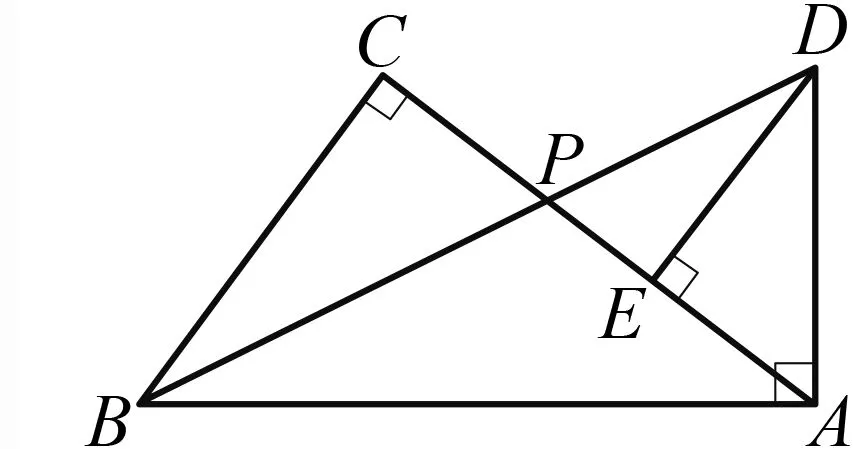
圖11

(1)求證：∠

CBP

=∠

ABP

；(2)若

AB

-

BC

=4，

AC

=8，求

AB

和

DE

的長度．解析 在(1)中，利用“等角的余角相等”即可證得．(2)中首先根據

AB

-

BC

=4，利用勾股定理求得

BC

=6，

AB

=10．作

PF

⊥

AB

于

F

，可證得△

BCP

≌△

BFP

，△

PAF

≌△

ADE

，進而求得

DE

的長．

例6

如圖12，在Rt△

ABC

中，∠

C

=90°，點

P

為

AC

邊上的一點，延長

BP

至點

D

，使得

AD

=

AP

=5，當

AD

⊥

AB

時，過

D

作

DE

⊥

AC

于

E

，若

DE

=4，則△

BCP

的面積為

．

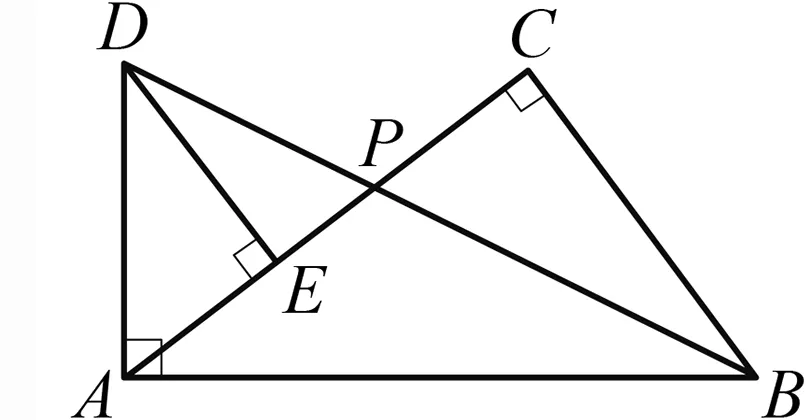
圖12

解析 直接求

BC

,

PC

的長度比較困難，△

ADE

的三邊長已知或者可求．過點

P

作

PH

⊥

AB

，可證得△

ADE

≌△

PAH

，△

PHB

≌△

PCB

，最后在Rt△

ABC

中，利用勾股定理求得

BC

,

BH

的長度，進而求得△

BCP

的面積．

3 擅用“框景”，鞏固提升

優秀的攝影者會在園林中拍攝出令人如癡如醉的作品，而園林的設計師又何嘗不是頂級的攝影者呢？所謂“框景”，就是設計師們有意識地在園林中設置很多框洞式的結構，引導游覽者在特定的位置上通過框洞來觀賞美景，更加方便地呈現園林之美．如圖13、圖14、圖15均是攝影愛好者站在既定的位置上拍攝出來的優秀作品，也體現了設計師高超的“框景”技藝．

圖13 圖14 圖15

在教學的過程中，教者也可以學習這樣的“框景”手法，在平時的教學過程中努力為學生創設更多的“機位”，讓學生能夠在教師的引導下獲取更加完整、更加美麗的“拍攝視角”，從而產出優秀的作品．比如“線段的最值問題”，一直是學習的難點，對于部分學生來說更是“談最值色變”，這就需要教師給學生搭建平臺，歸納概括出最值的常見解決方案，從而從心理和知識層面分別戰勝“最值問題”．面對例7這樣的題目，學生往往是茫然的，無從下手，教師應該在平時的教學過程中給學生提供一定的“腳手架”．

例7

如圖16，∠

MON

=90°，已知△

ABC

中，

AC

=

BC

=10，

AB

=12，△

ABC

的頂點

A

,

B

分別在射線

OM

，

ON

上，當點

B

在

ON

上運動時，點

A

隨之在

OM

上運動，△

ABC

的形狀始終保持不變，在運動的過程中，點

C

到點

O

的最小距離為

．

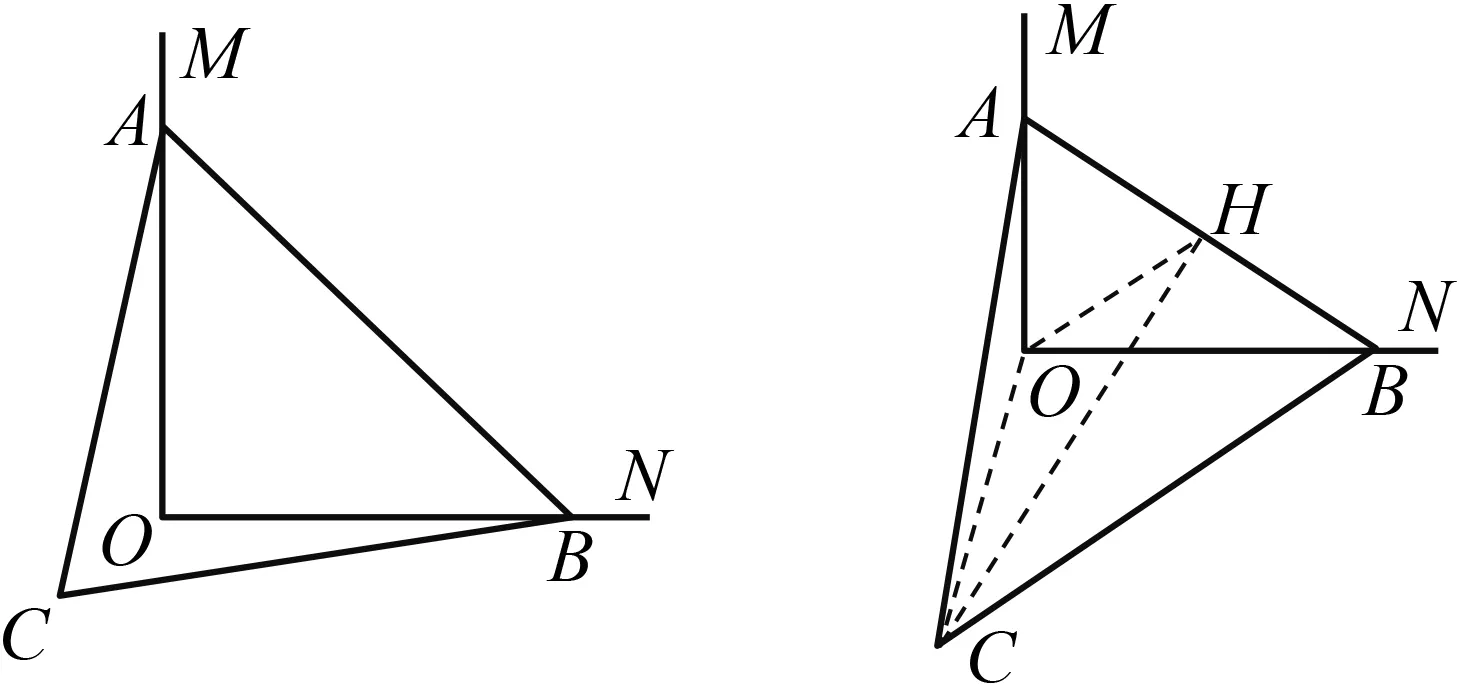
圖16 圖17

解析 如圖17，取邊

AB

的中點

H

，連結

OH

，

OC

，

CH

．由直角三角形斜邊上的中線等于斜邊的一半，可得

OH

=6，由等腰△

ABC

可求

CH

=8，在△

OCH

中，由“三角形的三邊關系”可得，

CO

的最小值為2．

例8

如圖18，在△

ABC

中，∠

ACB

=90°，∠

A

=30°，

AB

=5，點

P

是

AC

上的動點，連結

BP

，以

BP

為邊作等邊△

BPQ

，連結

CQ

，則點

P

在運動過程中，線段

CQ

長度的最小值是

．

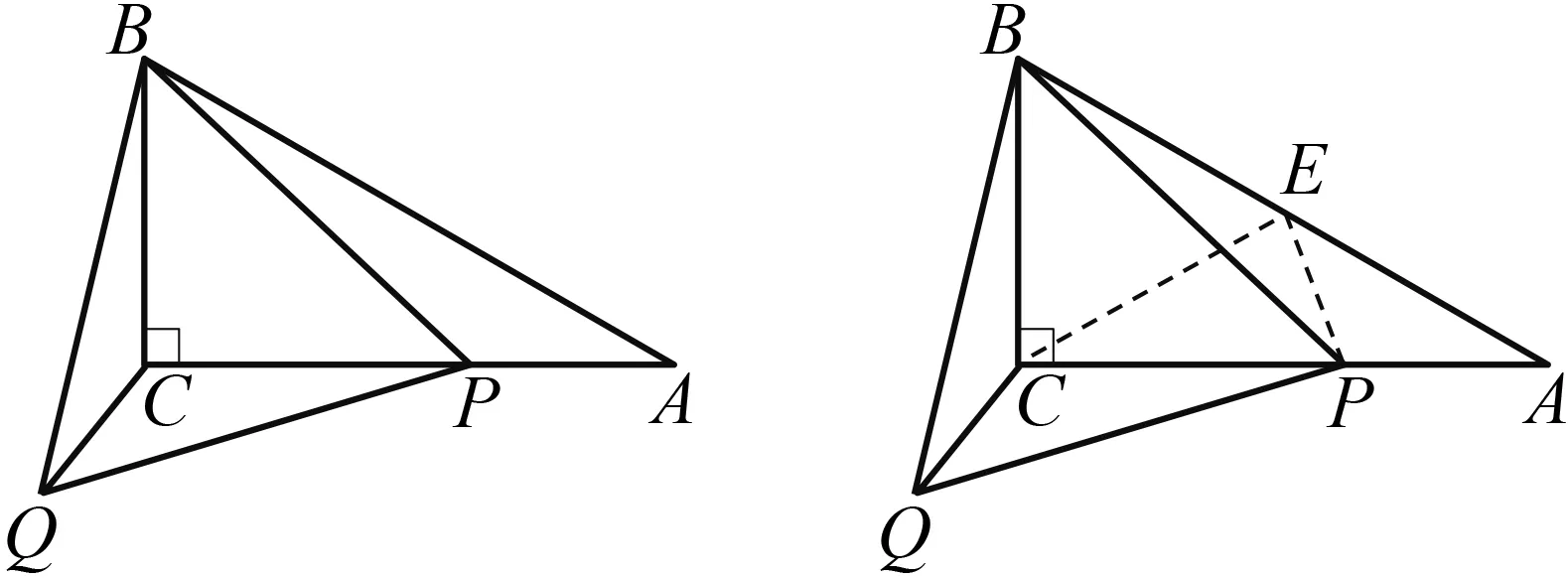
圖18 圖19

解析 如圖19，取邊

AB

的中點

E

，連結

CE

，

EP

．可證△

QBC

≌△

PBE

，實現了線段

CQ

到線段

EP

的轉化，再利用“垂線段最短”來求得線段

EP

的最小值．

這兩個例題有很多的相似之處，都是學生的難點，例7采用的是“三角形的三邊關系”模型解題，而例8所采用的是轉化條件后的“垂線段最短”手段，方式截然不同．如果平時不注重方法的總結，最容易出現“看起來會，做起來錯”的情況，甚至可能沒有任何思路．教師為學生選定了兩個相近的題目進行辨析解題，有助于學生辯證思維的發展，總結出求線段最值的常用方法：①將軍飲馬模型；②垂線段最短；③兩點之間，線段最短；④三角形三邊關系；⑤利用函數模型解題等．當學生再次遇到求線段最值的問題時，可以依次嘗試，找到適合的方法．若要實現以上效果，均要求教師能夠給學生同時見識不一樣的模型，“框”定基本的圖象模型，在固定的位置上總結反思解題方法，以期達到鞏固提升、“精準打擊”的良性循環．同時，這樣的培養方式也有利于學生數學抽象、數學建模等核心素養的形成．

4 活用“漏景”，自主探究

您一定欣賞過蘇州園林的美麗窗花，她們通過窗芯的彎曲變化形成了不同的圖案，精致、典雅，定勝紋、六角景、冰裂紋、魚鱗紋、古錢紋、海棠花紋等，數不勝數．融合了古代士大夫文人文化與民俗民間文化，徜徉在一扇扇窗花的背后，讓人不禁感慨吳地人民在長期的文化活動中所積累的璀璨智慧結晶．如圖20、圖21、圖22，都是園林中窗花的杰出代表．她們婀娜多姿的懷抱里透著背后更加美麗的景色，總讓人有種欲拒還迎的沖動，令人遐想萬千．

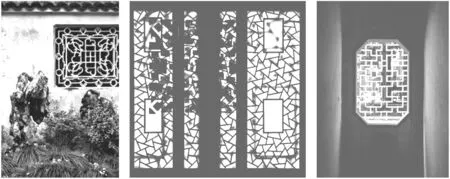
圖20 圖21 圖22

特級教師王曉峰說過：“評判一節好課的標準，就是看下課后學生是否久久不愿離座．”是啊，教是為了不教．如果一節課能夠激發學生的求知欲望，對于本節課的延伸知識有著渴望的求知欲，這不正是教師們所追求的理想效果嗎？在復習課階段，綜合題的解答會層出不窮，學生既有些許畏懼，又有幾分期待，如果我們能夠在講解的過程中給學生適當的延伸思考點撥，想必會激發學生的課后思考研究．

例9

已知△

ABC

中，∠

C

是其最小的內角，如果過點

B

的一條直線把這個三角形分割成了兩個三角形，其中一個為等腰三角形，另一個為直角三角形，則稱這條直線為△

ABC

關于點

B

的奇異分割線．如圖23，在Rt△

ABC

中，∠

A

=90°，∠

C

=20°，過頂點

B

的一條直線

BD

交

AC

于點

D

，且∠

DBC

=20°，則直線

BD

是△

ABC

的關于點

B

的奇異分割線．

圖23 圖24

(1)如圖24，在△

ABC

中，若∠

A

=50°， ∠

C

=20°．請過頂點

B

在圖24中畫出△

ABC

關于點

B

的奇異分割線

BD

交

AC

于點

D

，此時∠

ADB

=

°；(2)在△

ABC

中，∠

C

=26°，若△

ABC

存在關于點

B

的奇異分割線，且△

ABD

為直角三角形，請求出此時∠

ABC

的度數．解析 在解決(2)時，學生可以比較輕松地由△

ABD

為直角三角形進行三種情況的分類：①∠

BAD

為直角時，∠

ABC

=64°；②∠

ABD

為直角時，∠

ABC

=116°；③∠

ADB

為直角時，學生會發現△

BDC

不是等腰三角形，于是會選擇舍去這種情況，可是事實上，在這種情況下△

ABD

既是直角三角形又是等腰三角形，可以靈活地將△

BDC

看成直角三角形而△

ABD

看成等腰三角形，依舊是符合“奇異分割線”的概念要求的．對于這個題目，學生在熟知的三種直角情況分類基礎上又衍生出來特殊的情況，教師在講解的時候可以引導學生去掉條件“且△

ABD

為直角三角形”，學生定會將這個題目的所有情況有規則地一一討論出來．這有利于學生辯證思維的發展，同時也有利于學生邏輯推理、數學運算等核心素養的形成．

“引景—對景—框景—漏景”，在這些技藝的綜合運用之下，蘇州園林的美美得不像話，在我的教師生涯里，我也在努力探尋著屬于自己的“四景”．“人要往前走，花自向陽開”是少年的狀態；而“心守暖陽花自開，正得秋而萬寶成”則是中年的狀態．“風光不與四時同”，秋是四季里的中年，會讓有感覺的動物、有情趣的人類引起深沉、幽遠、嚴厲、蕭索的感觸來．體味著生命的內斂與深厚，緩慢而認真地前行，生命年輪在經年的旋轉中重味溫暖．