淺談地下結構的抗浮設計

姚 棋

（福州市城鄉規劃設計院有限公司，福建 福州 350007）

0 引言

隨著城市化進程的加快，城市可開發利用的地面空間愈發緊張，因此，對城市地下空間的開發利用迅猛發展，建設了一大批地下工程。隨著城市地下空間的大力開發，各類事故與災害也勢必增多，其中地下水對建筑結構的影響極大。雖然一些工程中地下室無水或者常水位較低，未發生工程事故，但每當暴雨過后地下水位急速升高，形成積水而無法及時消散時，地下水的上浮作用就可能會給地下室結構帶來嚴重的不可逆的破壞[1]。此外，部分結構設計師采用上部結構自重進行抗浮設計時，只片面地認為上部結構的自重標準值大于總的水浮力設計值時就滿足抗浮設計要求，而未分析上部結構自重荷載的分布和抗浮力的傳力路徑，從而造成局部范圍內抗浮壓力或抗浮拉力小于水浮力，導致地下室底板不規則隆起，甚至造成地下室以及上部結構構件發生大面積破壞。因此，結合具體工程特性，選擇安全、經濟、可行的抗浮措施，是地下建(構)筑物亟需解決的重要問題之一。

1 結構抗浮設計的基本概念

結構抗浮設計包括結構抗浮穩定設計和結構底板在水浮力作用下的強度設計。結構抗浮穩定問題為結構整體或局部在水浮力作用下因不能保持原來位置而發生的結構整體或局部上浮，這種上浮運動有可能是整體的剛體運動，也可能是因為結構某部分的上浮運動受到約束而使結構體產生較大的變形破壞；結構底板在水浮力作用下的強度問題僅僅是基礎底板在凈水浮力下的強度破壞，與恒活載作用下的強度破壞形式沒有區別。

兩類問題的主因相同，都是水浮力的作用，與地下水位的高低有密切的關系。一般來說，存在抗浮穩定問題的工程，必然存在基礎底板在水浮力作用下的強度問題。但存在水浮力作用下基礎底板強度問題的工程，不一定存在抗浮穩定問題，關鍵在于抗浮設防水位的高低。

（1）當抗浮設防水位低于基礎底板，此時既不存在結構底板在水浮力下的強度問題，也不存在結構的抗浮穩定問題。

（2）當抗浮設防水位高于基礎底板，由水浮力工況控制但水浮力合力尚未超過建筑物結構自重與附加恒載的合力時，基礎底板存在強度問題，整個結構體尚不存在整體的抗浮穩定問題，但不排除結構體局部存在抗浮穩定問題。當抗浮設防水位繼續升高，僅靠結構自重及附加恒載無法平衡水浮力，就存在結構整體的抗浮穩定問題，也必然存在基礎底板在水浮力下的強度問題。

2 工程概況

福建省福州市晉安區某鎮一工程，由2幢6F辦公樓、2層地下室組成，柱網為8.4m×8.4m，采用600mm厚筏板基礎（局部沖切不夠，加厚處理），如圖1所示。該工程±0.00m相當于羅零高程37.100m，根據地勘資料，抗浮設防水位建議采用36.50m（羅零高程）。底板面標高為-8.500m，疏水層厚100mm，地下室水頭高度為8.5m。

圖1 筏板基礎局部平面布置

3 結構抗浮設計的主要內容

結構抗浮設計的主要內容包括兩部分：（1）結構構件（筏板、防水板、地下室外墻等）在水壓力作用下的強度設計（截面尺寸與配筋）；（2）地下水浮力作用下的整體與局部抗浮穩定性設計。嚴格意義上，二者計算水浮力時所采用的水頭并不一定相同，抗浮穩定計算的水頭一般要高于結構構件強度計算的水頭。

3.1 結構構件強度設計

（1）防水板荷載的計算。防水板及其疏水層自重：

qs1=25×0.6+20×0.1=17kN/m2

水浮力標準值：

qw=10×8.5=85kN/m2

防水板荷載設計值：

qwj=1.5×85-1.0×17=110.5kN/m2

（2）防水板的受力計算。

防水板按無梁樓蓋設計，如圖2所示。

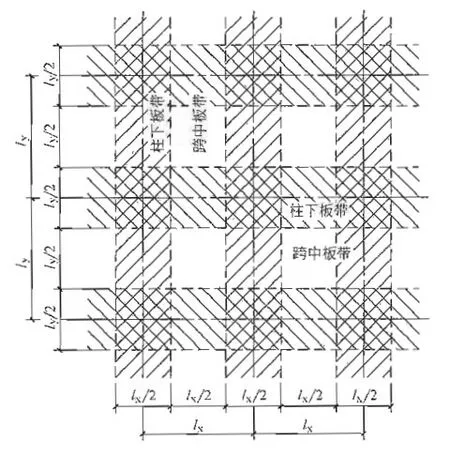
圖2 無梁樓蓋的板帶劃分

其中：bce=4.2 m,lx=ly=8.4 m,q=qwj=110.5kN/m2

Mx=My=qly(lx-2bce/3)2/8=110.5×8.4×(8.4-2×4.2/3)2/8=3465.28kN·m

防水板彎矩：

柱下板帶：M1支=0.5×3465.28=1732.64kN·mM1中=0.18×3465.28=623.75kN·m

跨中板帶：M2支=0.17×3465.28=589.1kN·mM2中=0.18×3465.28=519.8kN·m

防水板的配筋設計：

柱 下 板 帶：As,1支=M/(0.9fyh0)=1732.64/(0.9×360×1.16)=4610.05mm2

As,1中=M/(0.9fyh0)=623.75/(0.9×360×0.56)=3437.78mm2

跨中板帶：As,2支=M/(0.9fyh0)=589.1/(0.9×360×0.56)=3246.80mm2

As,2中=M/(0.9fyh0)=519.8/(0.9×360×0.56)=2864.86mm2

最小構造配筋：As,min=0.15%bh=0.15%×1000×600=900mm2

故防水板配筋率為計算配筋控制，不是構造配筋控制。

3.2 抗浮設計

抗浮設計包括兩部分內容：（1）整體抗浮，要求建筑物自重和壓重之和大于水的浮力，保證地下結構整體不上浮；（2）局部抗浮，保證地下室局部構件，如基礎底板、地下墻體、梁柱節點不出現局部應力較大而發生開裂或變形[2]。

3.2.1 整體抗浮

依據《建筑地基基礎設計規范》(GB 50007—2011)[3]，建筑物基礎存在浮力作用時應進行抗浮穩定性驗算。

式中：

Gk——建筑物自重及壓重之和，kN；

Nw,k——浮力作用值，kN；

Kw——抗浮穩定系數，一般情況下可取1.05。

依據《建筑工程抗浮技術標準》（JGJ 476－2019）[4]，建筑工程抗浮穩定性應符合式（2）規定：

式中：

G——建筑結構自重、附加物自重、抗浮結構及構件抗力設計值總和，kN；

Nw,k——浮力設計值，kN；

Kw——抗浮穩定安全系數。

根據地勘資料，該工程建筑抗浮設計等級為乙級，水文地質條件復雜程度為中等復雜。故使用期的抗浮穩定安全系數為1.05，與《建筑地基基礎設計規范》(GB 50007—2011)[3]的規定一致。

通過盈建科軟件計算得到此工程的整體抗浮數據如表1所示。

表1 整體抗浮數據計算結果

綜上所述，此工程整體抗浮滿足設計要求。

3.2.2 局部抗浮

依托工程局部浮力最不利處為2#主樓下的兩層地下室，室外覆土厚度為1m，室內±0.00相當于羅零高程37.100m，根據地勘資料，抗浮設計水位建議采用36.50m（羅零高程）。

取最不利柱網尺寸8.4m×8.4m進行計算，地下一層頂板厚250mm，地下二層頂板厚250mm，均為梁板式樓蓋，底板筏板厚600mm，面層厚100mm，基礎底標高為-9.00m；上部樓層共6層，標準層板厚120mm，屋面板厚120mm，樓層恒載標準值為1.5kN/m2,屋面恒載標準值為4kN/m2。

（1）抗浮計算。

①地下室恒載。

柱子自重：25×8.4×0.6×0.6=75.6kN

頂板自重：25×0.25×2×8.4×8.4=882kN

底板自重：25×0.6×8.4×8.4=1058.4kN

疏水層自重：20×0.1×8.4×8.4=141.12kN

恒載自重：1.5×8.4×8.4×2=211.68kN

則地下室恒載為：

G1=75.6+882+1058.4+141.12+211.68=2368.8kN

②上部樓層恒載。

柱子自重：25×3.6×0.5×0.5×6=135kN

樓層梁板自重：

(25×0.3×0.7×8.4×2+25×0.3×0.55×8.4×3+25×0.12×8.4×8.4)×6=2423kN

樓層恒載：1.5×8.4×8.4×5=529.2kN

屋面板恒載：4×8.4×8.4=282.24kN

則上部樓層恒載為：

③恒載總重：

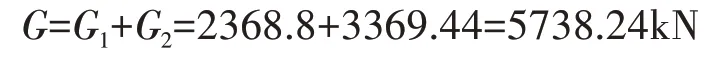
④水浮力：

即F>G，僅依靠結構自重不滿足抗浮要求。

（2）抗浮方案的選擇。

①壓重法：

依據《建筑工程抗浮技術標準》（JGJ 476－2019）[4]，壓重抗浮法穩定性應滿足式（3）要求：

式中:

G——結構自重及其上作用的總荷載標準值，kN；

Gt——增加的壓重荷載標準值，kN；

S——驗算單元面積上浮力標準值總和，kN；

Ks——抗浮穩定性安全系數，該工程取1.05。

即G+Gt=5738.24+Gt=5927.04×1.05，則Gt=485.152kN

若增加頂板厚度，則：

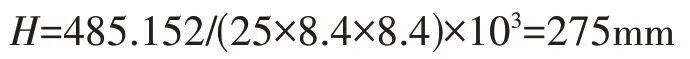
若選擇增加底板厚度，則因為增加了防水板的底標高，浮力S也增加了，實際增加的抗浮自重G=H×(25-10-1.05)×8.4×8.4，所以增加筏板底厚度的方案不經濟，不予以考慮。

②壓重法+局部抗浮錨桿：

依據《建筑工程抗浮技術標準》（JGJ 476－2019）[4]，壓重法與抗浮錨固構件聯合抗浮時，抗浮穩定性應滿足式（4）要求：

式中：

ΣR——錨固構件抗拔承載力標準值總和，kN。

經計算可得ΣR=485.152kN

根據《建筑工程抗浮技術標準》（JGJ 476－2019）[4]，錨桿直徑d=200mm，采用二次注漿，打入土層深度13m。

土層錨桿錨固長度應按式（5）計算：

取Nt=250kN

則n=485.152/250=1.95≈2

綜合現場實際及經濟效益等方面考慮，此工程采用壓重法+局部抗浮錨桿的抗浮方案，抗浮錨桿集中布置在柱網附近，但是并非所有工程的抗浮設計都適合用此方法，此方法只適合于在滿足地下結構整體抗浮穩定的基礎上，還需要考慮局部抗浮的工程。若整體抗浮都不滿足要求，則不適用此方法[5]。

4 結束語

綜上所述，地下結構中的抗浮設計直接關系到結構的穩定性與安全性。在進行結構抗浮設計時，需結合工程地質特點，通過技術、經濟等多方面的論證，選擇合理的計算方法以及正確的計算模型對結構構件在水壓力作用下的強度和地下水浮力作用下的整體與局部抗浮穩定性進行設計，并科學地選擇抗浮措施。