質子交換膜燃料電池氫循環噴射器的組分輸運與相變研究＊

孫文慧，梁麗華

(山東建筑大學信息與電氣工程學院，山東 濟南 250101)

0 引言

汽車的普及和發展一直伴隨著石油消費危機和空氣污染危機。質子交換膜燃料電池以氫為燃料，具有零污染物排放、啟動速度快、工作溫度低、結構緊湊等特點，是替代內燃機(ICE)最有前景的技術[1]。

噴射器因結構簡單、無運動部件、無寄生功率等特點正逐漸取代傳統的機械泵，回收利用未消耗的氫氣和水蒸氣，提高PEMFC 系統的性能，成為近年來的研究熱點[2]。PEMFC 陽極側氫罐中釋放的氫氣作為高壓一次流，進入噴射器，引射循環回路中未消耗的氫氣和未排盡的水蒸氣；流體在噴射器中混合，作為燃料輸送到電堆。噴射器需充分回收未消耗的氫，及時排出產生的液體水。

迄今為止，對PEMFC系統陽極氫氣再循環噴射器的研究數量有限，主要集中在利用CFD 方法進行機理研究和優化。Feiqiang Li.[3]等考慮吸入流體中水蒸氣質量分數，設計了一種具有匯聚噴嘴和圓柱形混合管的噴射器，在PEMFC 系統內達到預期的摩爾再循環比。文獻[4]基于剪切應力等輸運模型，建立了噴射器二維軸對稱模型，結果表明，二次流濕度和混合室直徑對氫氣再循環率有顯著影響。由上述文章可知，噴射器陽極氫氣再循環中，二次流濕度在20%～100%左右，且由多種氣體組成，必然會對噴射器性能產生影響。

不同工況下復雜的內部流動結構對噴射器性能有很大的影響，成為近十年來噴射器研究的主要課題。Croquer[5]基于熱力學雙方程湍流模型，觀察激波列沿線的高壓和低壓區域。文獻[6]顯示在沖擊波和邊界層處出現了最大流速約1.8 馬赫，伴隨著清晰的、明顯的壓力變化。同時，噴射器內復雜的超聲速流體動力學、壓力變化、高湍流等使得蒸汽凝結和相變的現象受到越來越多的重視[7]。Wang等[8,9]采用濕蒸汽模型研究了過熱蒸汽液位對噴射器內冷凝液滴半徑、液滴數量、液分數和引射性能的影響，完成了噴射器的結構設計。

多篇文章針對一次流和二次流均為水蒸氣的工況，對噴射器內的凝結和相變進行了研究[7-9]。然而，在PEMFC 系統中，噴射器的一次流是氫氣，而二次流是氫氣和水蒸氣的混合物。噴射器內工作流體的變化會引起氣體粘度、密度等熱機械參數的變化，這些變化對冷凝現象有重要影響。此外，之前文獻研究的噴射器內冷凝過程幾乎發生在制冷和MED-TVC 系統中，二次流和出口流體相互獨立。相反，在PEMFC系統中，二次流和出口流體的參數是強耦合的。

本研究的主要貢獻在于：建立了一種組分輸運-相變模型，并將其應用于PEMFC 系統中陽極再循環噴射器的流動動力學特性分析和操作性能評價。

1 噴射器模型

用于PEMFC 系統陽極再循環的噴射器由五部分組成，如圖1 所示：噴嘴、吸入室、混合室、等面積段和擴散段。一次流氫氣在收斂噴嘴內擴大速度，降低壓力。由于壓差，吸入室內超音速氫氣損失部分動能，由二次流入口吸入未消耗的氫氣和水蒸汽。兩種流體在混合室中混合，進行復雜的能量交換，在等面積段和擴散段發生剪切混合，具有一定濕度和壓力(背壓)的混合流體在出口處被送到燃料電池電堆。

圖1 PEMFC系統陽極再循環噴射器結構圖

為了研究噴射器內流體動力學特性，本文提出組分輸運-相變模型，控制方程由質量、動量和能量守恒方程來描述。為了模擬多相流體動力學，可以采用Mixture模型求解混合相的動量、連續性和能量。由此得到各相體積分數、各組分質量分數和相對速度的代數表示。

⑴在混合物模型中，連續性方程，即二維軸對稱結構的質量守恒方程，由式⑴得到：

其中，ρm為混合物的密度，?為標量的梯度或矢量的梯度(二階張量)為混合物的平均質量流量。

考慮組分輸運，利用對流擴散質量守恒方程式⑵預測各組分的局部質量分數：

其中，ρ是混合物密度，mj是第j個組分質量分數是第j個組分由于濃度和溫度梯度的擴散通量，Rj是化學反應生成速率，Sj是用戶定義的反應生成速率。

對于第k相，求解對流擴散方程(3)來預測各組分的局部質量分數。

其中，αk為第k相的體積分數，mjk為第k相中第j組分的質量分數為第k相的質量流量，mki→pj為第k相到第p相中第i組分和第j組分之間的質量傳輸。

將各相的動量方程求和，得到動量守恒方程，由公式⑷給出：

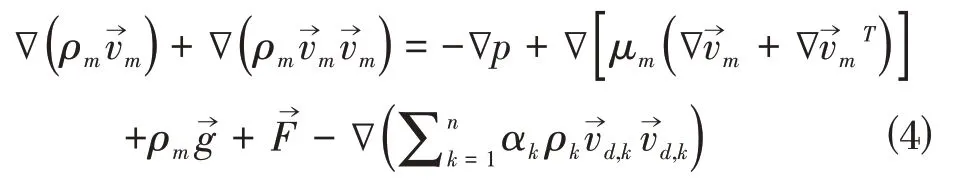
其中，n為相的個數，μm為混合物粘度為外部體積力為重力體積力。

能量守恒方程定義為式⑸：

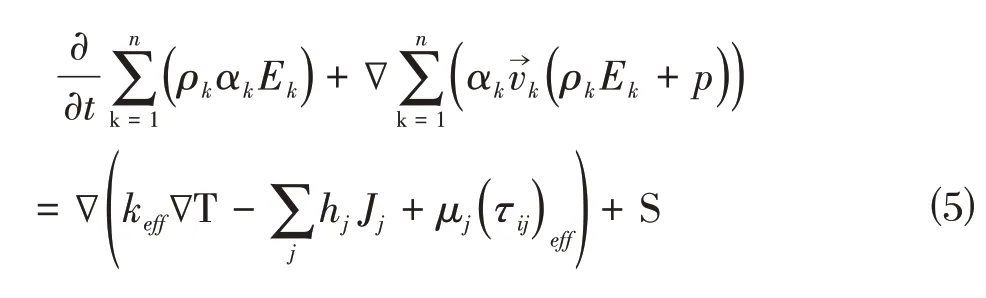
2 計算流程

2.1 邊界條件

根據電堆輸出功率和運行狀態調整噴射器的工作參數。本研究根據中國弗爾賽能源公司設計的RDZ04 系列PEMFC 的實際運行工況進行參數的設置，電堆輸出功率為40kW～70kW，噴射器運行參數如表1所示。

表1 PEMFC系統內噴射器運行工況

2.2 數值計算過程

利用CFD 預處理軟件GAMBIT GUI 將噴射器的幾何形狀劃分為若干規則區域，生成網格?；疚锢砟Ｐ?、湍流模型、多相流模型、部件輸運模型和求解器均使用流行的商用CFD 軟件包Fluent 18.0 實現。采用Besagni 討論的與實驗數據吻合較好的RNG k-ω模型，考慮湍流旋渦的低雷諾數流動的黏度。

考慮液體流動連續性的特點，多相模型采用歐拉-歐拉模型求解混合相的動量、連續性和能量方程、二次相的體積分數方程以及相對速度的代數表示。組分輸運模型選擇混合物物料，考慮各組分的質量分數，確定混合物的密度、比熱、導熱系數和粘度等物理性質。

3 實驗結果

圖2 為基于組分輸運-相變模型和干蒸汽模型預測的噴射器內部壓力分布圖。一次流體在噴嘴入口壓力約為6.99 bar，隨著噴嘴的收斂，壓力減??；在噴嘴出口，壓力達到最小值，遠低于二次流進口的1.65 bar，且壓力出現不規則變化。混合室下游的壓力逐漸增大，在噴射器出口處壓力在2bar 左右，滿足電堆的需求。干氣模型計算的壓力分布變化大于組分輸運-相變模型，且波峰波谷值的出現將對較早。由此表明凝結現象產生的液滴促進了氣液兩相的換熱，減緩和推遲了壓力振蕩，減小壓力波動時的誤差。

圖2 基于組分輸運-相變模型和干蒸汽模型的噴射器內流體壓力云圖

圖3 為基于組分輸運-相變模型和干蒸汽模型計算的噴射器內部速度分布圖。噴射器內速度分布變化方向與壓力分布變化方向幾乎相反，這是由于壓力勢能與動能相互轉換所致。兩種模型的激波形態相似，但局部速度存在一定差異。對于第一峰值，相變模型的馬赫數在2.00 左右，而干蒸汽模型馬赫數為1.98；第一谷值相變模型馬赫數約為1.60，干蒸汽模型馬赫數約為1.49；兩模型在等面積段和擴散段的最大馬赫數差約為1.71；這意味著低估了膨脹程度可能會導致基于干蒸汽假設的引射比被低估。

圖3 基于組分輸運-相變模型和干蒸汽模型的噴射器內流體速度云圖

圖4(a)和圖4(b)顯示了不同濕度和壓力下引射比波動情況。在一定條件下，由組分輸運-相變模型計算的引射比比由干蒸汽模型計算的值高13.2%，誤差低約5.6%。這表明，組分輸運-相變模型可以更準確的預測不同狀態方程和流體性質(密度、比熱、粘度等)，比干蒸汽模型更適合分析噴射器內部流動結構和性能。

圖4

4 結論

噴射器對于PEMFC 系統來說是至關重要的，它可以將未消耗的氫氣再循環。本文針對噴射器二次流含有多種氣體且內部流體結構復雜，建立了組分輸運-相變模型，并利用流行的商業CFD 軟件包Fluent進行仿真。通過與干蒸汽模型對比發現，考慮相變和組分輸運后，考慮與凝結相關的熱傳質，壓力分布最大差異約14.3%，等面積段和擴散段馬赫數最大差約1.71，引射比更高。因此可以得出結論，在預測PEMFC系統噴射器的流動特性和引射性能時，必須重視組分輸運、冷凝和相變現象。