基于三電平逆變器和模型預測的電機控制方法

姜澤超，朱蘊璞，孫 樂，高 鵬

(1.南京理工大學 機械工程學院，南京 210014；2.南京理工大學 自動化學院，南京 210014)

0 引 言

永磁同步電機具有結構靈活、體積小、質量輕、效率高、功率因數高等顯著特點[1]，因此在運動控制中得到了廣泛使用。由于存在外部干擾、不確定性和非線性等問題，傳統的線性控制方法，包括比例積分(PI)控制方法，并不能在控制過程中保證伺服系統具有足夠高的控制性能[2]。為了提高伺服系統的控制性能，近年來，隨著控制芯片微處理器性能的提高，一些現代控制理論中常用的控制策略被運用到永磁同步電機控制中，例如線性化控制[3]、自適應控制[4]、魯棒控制[5]、滑模控制[6]、模糊控制[7]等。

采用多電平逆變器驅動是一種能夠有效降低永磁同步電機電流諧波的方法[8]。三電平逆變器是應用比較廣泛的多電平逆變器，由于拓撲結構的差異，三電平逆變器能輸出三個電平，輸出電壓和電流諧波相較于兩電平逆變器更小。同時，三電平逆變器的開關管個數比兩電平逆變器多，同樣的輸出電壓下，每個開關管所需承受的電壓更低，因此在保證逆變器安全運行的情況下，能夠提高開關頻率，輸出諧波進一步降低[9]。

大慣量隨動系統的負載慣量大且在工作過程中實時變化，對其伺服控制是較為復雜的問題。對于這類復雜的控制問題，一些傳統的控制方法如PI控制、模糊控制、自適應控制等并沒有針對負載慣量時變的特點進行研究，不能提供很好的控制性能。

模型預測控制(以下簡稱MPC)是工業應用中最實用的先進控制技術之一[12]。永磁同步電機伺服系統的控制策略可以看成是一個最優化問題，而MPC是一種最優控制方法，它在每個采樣時間內對有限集內的某個目標函數的代價函數進行在線尋優，以此來預測狀態的未來行為[13-14]。

文獻[15]了優化永磁同步電機伺服系統的控制性能，將MPC方法引入速度環的控制設計中，采用簡化模型預測永磁同步電機未來的q軸電流，通過最小化二次型性能指標得到最優控制律。文獻[16]將MPC運用到負載系統的控制策略中，建立了大慣量隨動系統負載的動力學模型，并考慮系統性能指標、能量輸入功率和制動功率等約束條件，實現了大慣量隨動系統的MPC。

MPC在控制過程中若受到了強干擾的影響，可能會導致控制性能的下降。文獻[15]研究了永磁同步電機的擴展狀態觀測器(以下簡稱ESO)速度控制方法，ESO比通常的狀態觀測器高一階，用于估計狀態和集中擾動，永磁同步電機速度外環采用狀態反饋控制器，通過ESO將負載轉矩估計為擾動，仿真和實驗驗證了該方法的可行性。文獻[17]針對永磁同步電機系統中的強擾動問題，引入了ESO來估計集中擾動，且在速度控制器中添加了基于估計擾動的前饋補償項，并通過仿真和實驗驗證了該方法的有效性。

MPC能夠在控制器中將大慣量隨動系統的約束包含在內并進行控制，因此對于大慣量隨動系統這類復雜的控制問題，MPC能提供較好的控制性能。但是MPC方法的抗干擾性能較差，為了提高MPC方法在整套控制方案中的抗干擾性能，在MPC反饋部分的基礎上，在速度控制器中添加了基于估計擾動的前饋補償項。本文提出了一套二極管箝位型(以下簡稱NPC)三電平逆變器、MPC與ESO相結合的復合控制方案，并將該方法應用于驅動系統，提高了擺臂機構的動態響應與控制精度。

1 擺臂結構驅動系統動力學模型

該驅動系統主要由永磁同步電機和由負載以及連接軸組成的擺臂結構構成。擺臂結構在永磁同步電機作用下做到位控制。擺臂結構電機驅動系統結構示意圖如圖1所示。

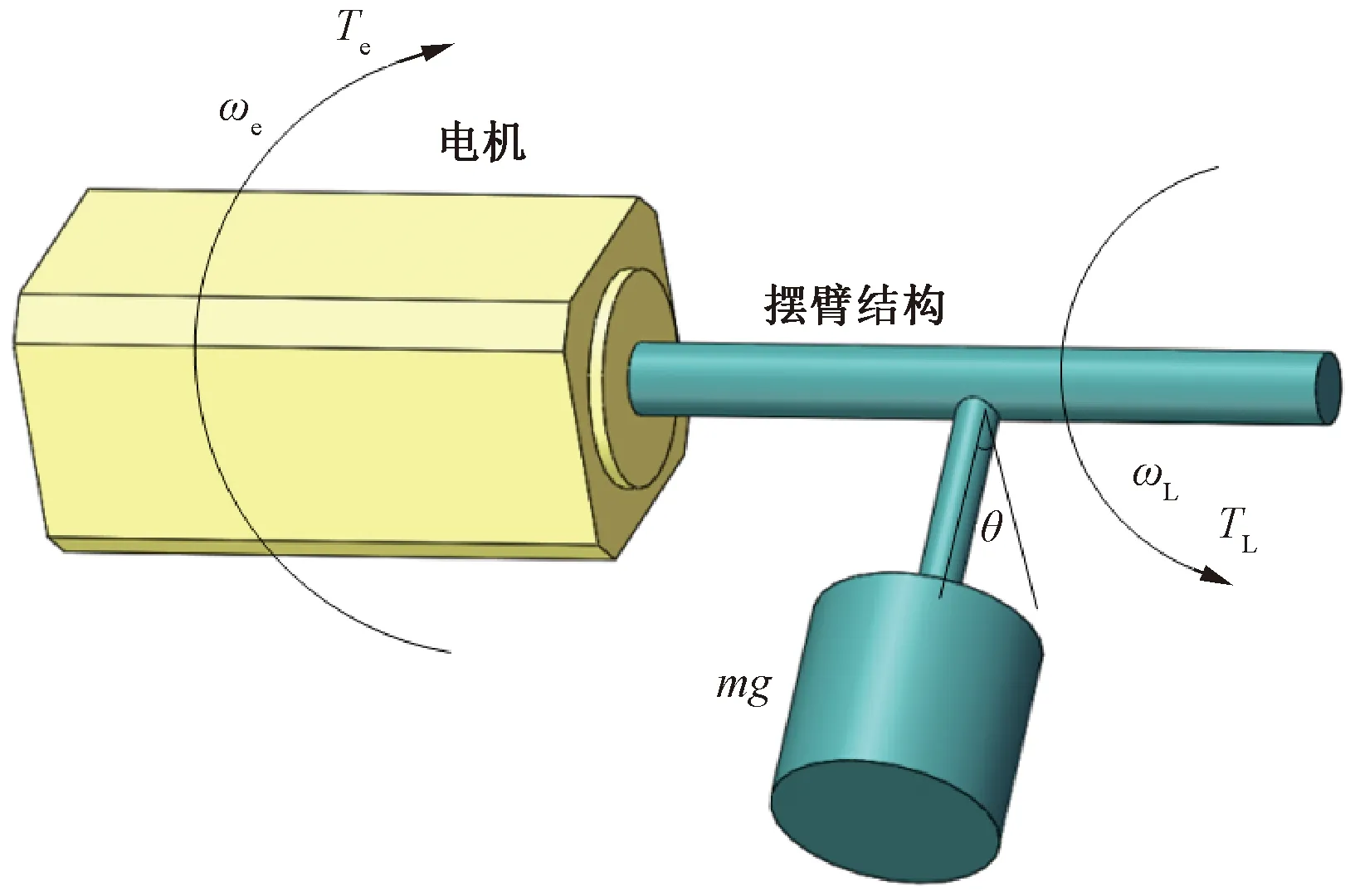
圖1 擺臂驅動系統結構示意圖

1.1 永磁同步電機的數學模型

永磁同步電機在d-q坐標系下轉矩方程：

Te=p[ψfiq+(Ld-Lq)idiq]

(1)

式中：id，iq為d，q軸下的定子電流；p為電機極對數；Ld，Lq為d，q軸下的電感；ψf為磁鏈。

表貼式永磁同步電機的Ld=Lq，則式(1)化簡：

(2)

1.2 擺臂驅動系統機械運動方程

在擺臂結構驅動系統中，永磁同步電機根據給出的位置指令輸出動力，驅動擺臂結構進行回轉運動，且通過編碼器來實時獲得擺臂的位置反饋，來計算后續的控制序列。基于大慣量單電機直驅系統的數學模型，本文的擺臂機構伺服系統的數學模型：

(3)

式中：Te為電機的電磁轉矩；J為折算到電機軸上的總轉動慣量；θrm為電機軸機械角位置，也是負載和豎直方向夾角；負載轉矩TL=mgLarm，mg是負載重力；D是摩擦系數。

2 基于MPC算法的控制系統

2.1 NPC三電平逆變器的驅動原理

NPC三電平逆變器廣泛應用于工業領域[19-20]，其結構包括12個開關和6個箝位二極管。

NPC三電平逆變器的拓撲結構如圖2所示，其中開關Sx1和Sx2、Sx3和Sx4是互補狀態。在永磁同步電機控制系統的電流環中，NPC三電平逆變器可以產生比傳統兩電平逆變器更高的開關頻率，以降低電流諧波分量(THD)。

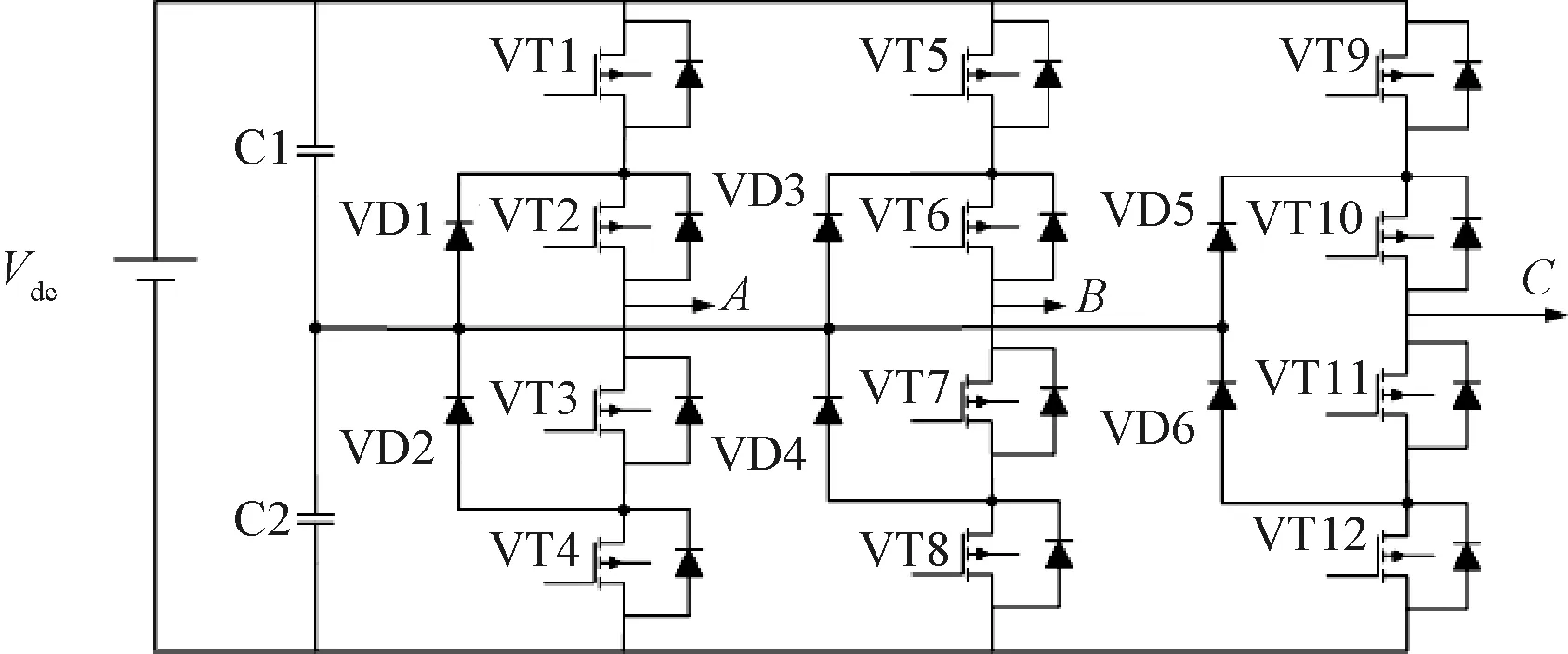
圖2 NPC型三電平逆變器拓撲

由于共有12個開關，NPC三電平逆變器共有27種開關狀態可用。這些開關狀態可以在靜止軸上產生27個電壓矢量，包括8個冗余電壓矢量和18個非冗余電壓矢量。NPC三電平逆變器的可用電壓矢量如圖3所示。NPC三電平逆變器的開關狀態和相電壓如表1所示，其中x=a、b、c。

圖3 NPC三電平逆變器的有效電壓矢量

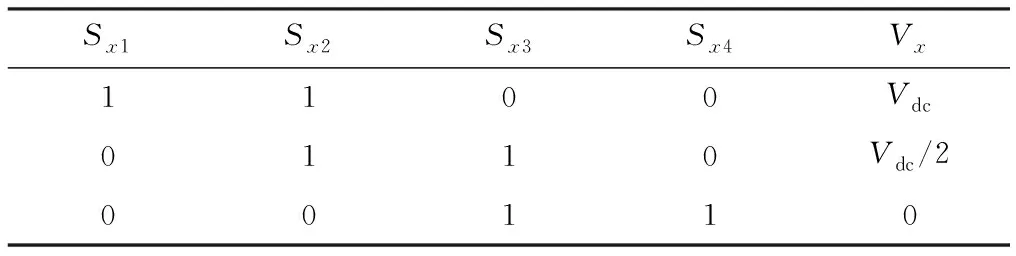
表1 NPC三電平逆變器的開關狀態和輸出電壓

NPC逆變器的直流側有2個電容串聯分壓，因此，當2個電容的中點電壓平衡時，才能保證驅動系統正常可靠運行。如果中點電壓不平衡，輕則降低逆變器的輸出效率，影響電機的調速性能，嚴重時會對逆變器中的電容和開關管造成損壞。而造成中點電壓不平衡的原因是多方面的，比較常見的有[25]：

(1)現實中，兩個電容的容值不可能完全相等，從而造成中點電壓的恒定偏置；

(2)中點電壓的波動會隨著直流側電容的容值變化，容值越小，波動越嚴重；

(3)中點電流能夠直接反映出定子電流的大小，當負載轉矩增大時，中點電流增大，波動越嚴重。

2.2 MPC算法的控制原理

MPC控制原理如下：在每一個采樣時刻，根據當前獲得的各項用于預測的信息量，先建立一個預測模型，并對模型輸出與實際輸出之間的誤差進行校正，然后給出一種控制律，使得被控信號能夠跟蹤參考軌跡，最后通過一種滾動優化的方式得出一個被控信號到參考軌跡之間的最優過渡，并將得到的結果序列中的最優結果作用于被控對象。

MPC一般由以下幾個部分組成：

(1)基函數：在MPC中，將輸入表示為已知基函數ubj的線性組合[26]：

(4)

式中：N為基函數的個數；uj為性能指標優化過程中需計算的參數；P為預測時域；ubj(i)為基函數在t=iTs時刻的值；Ts為采樣時間。

(2)預測模型：MPC中需要一個線性的數學模型用于在線預測有限時間內的未來輸出。這個預測模型通常為離散形式：

xm(k)=Axm(k-1)+Bu(k-1)k=1,2,…

(5)

(6)

式中：xm(k)為模型的狀態向量；A，B，C為模型狀態方程的系數矩陣；ym(k)為模型輸出部分。

(3)校正誤差：由于外部和自身的影響，通過預測得到的結果存在誤差是不可避免的，將誤差校正為如式(7)所示的情況，以表示預測輸出和實際輸出之間的誤差：

e(k+p)=…=e(k+1)=e(k)=y(k)-ym(k)

(7)

式中：y為被測系統的輸出值。

(4)參考軌跡：給出一個參考軌跡，并找到一種控制律，如式(8)所示，使得在該控制律內被控信號能夠跟蹤參考軌跡：

(8)

(5)滾動優化：通過對跟蹤誤差和對控制輸入的計算，得到一個最優指標，使系統輸出的最優過渡會盡可能接近參考軌跡：

(9)

式中：M為控制時域；參數qi允許強調每個受控輸出及其預測；rj為衡量控制輸入的性能。

2.3 驅動系統設計的原理框圖

本驅動系統原理框圖如圖4所示。從圖4可以看到，NPC三電平逆變器、模型預測控制器以及PI設計等構成了該驅動系統。

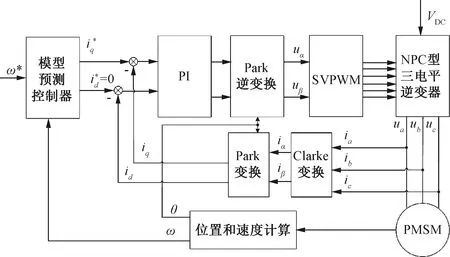
圖4 驅動系統原理框圖

2.4 控制器設計

由于系統的阻尼比較小，所以將D視為0處理，式(3)可以重新構建如下：

(10)

由于MPC的預測模型需要為離散形式，所以將式(10)離散化，得到：

TLcos[θrm(k)]}

(11)

式中：Ts為速度環采樣周期。通過MPC模型得到的速度預測的離散方程，可以由式(11)得出：

ω(k+1)=ω(k)+TsF{iq(k),θrm(k),

TLcos[θrm(k)]}

(12)

式中：F[·]是包含非線性分量的控制項函數向量。

參考軌跡：

(13)

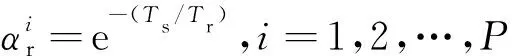
誤差矩陣如下式：

E(k)(P×1)=[e(k)…e(k+P)]

(14)

式中：e(k)=ω(k)-ωm(k)表示電機的實際速度ω(k)與通過MPC預測得到的速度ωm(k)之間的誤差。

預測將來行為的第itd步，參考軌跡的轉速ωr(k+i)與電機實際轉速ω(k+i)之間的差值如下式：

ωr(k+i)-ω(k+i)=ωr(k+i)-

ωm(k+i)-e(k+i)

(15)

為了使上述值最小，建立求解式：

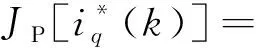
(16)

那么，可以通過求解式(17)來獲得在kth步的最優參考電流iq*：

(17)

最后采用牛頓迭代法來尋找式(17)的最小值。其中一次迭代如下式：

(18)

式中：n為在每一步預測中的迭代次數。

為了提高MPC方法的抗干擾性能，在速度控制器中除了MPC反饋部分外，還引入了對干擾的前饋補償部分。ESO作為一種干擾估計技術被引入速度控制系統。圖5為MPC+ESO控制器的原理框圖。

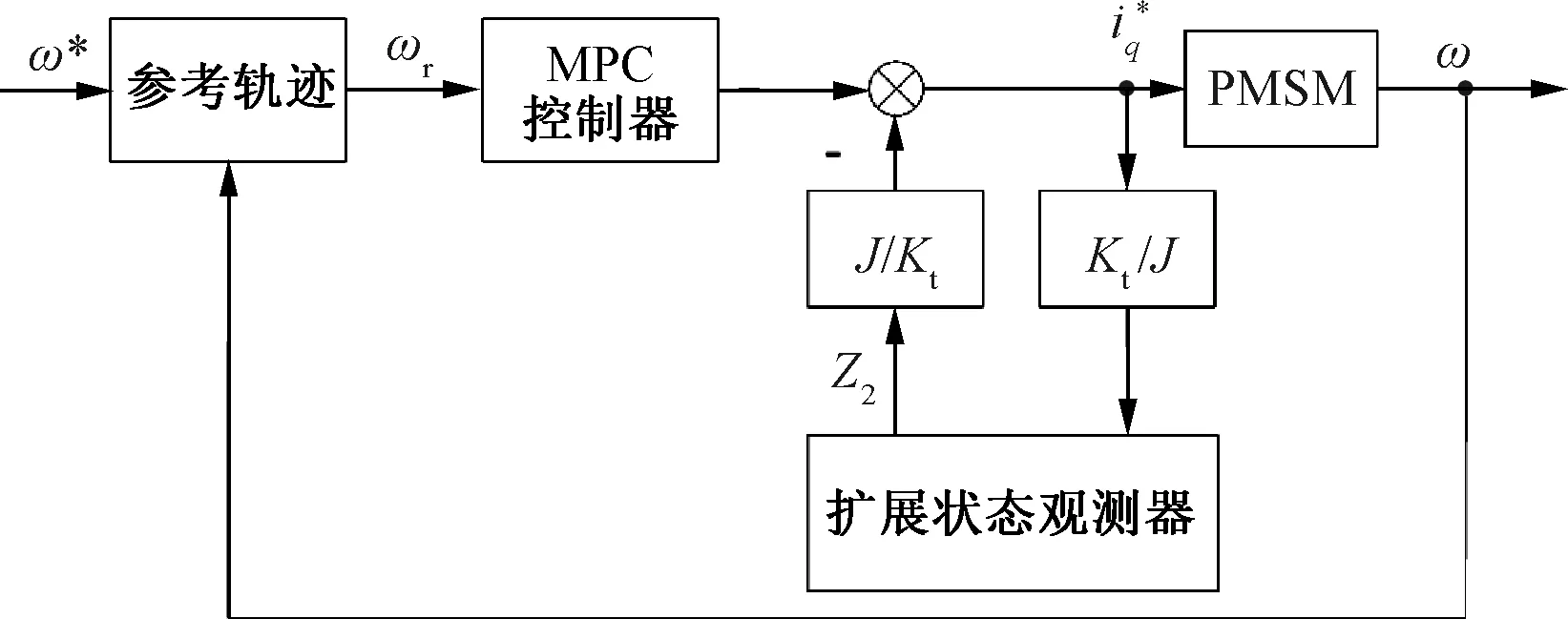
圖5 MPC+ESO原理框圖

由圖5可得，MPC+ESO控制器的輸出為ω。考慮到扭轉力矩和系統擾動，永磁同步電機的機械運動方程可以表示：

(19)

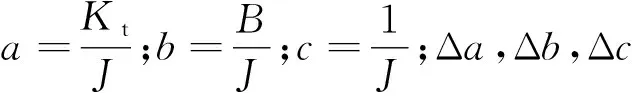
(20)

式中：d(t)表示系統集總擾動。因此式(19)可以表示：

(21)

令x2=d(t)為擴展的狀態量，c(t)為擾動的變化率。因此式(20)可擴展：

(19)

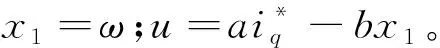
(20)

式中：-p為擴展狀態觀測器的極點，并且p>0；z1為速度ω的估計值；z2為系統集總擾動d(t)的估計值；根據文獻[24]，z1(t)→ω(t)，z2(t)→a(t)。基于此信息，可以實現干擾補償。

借助于ESO，系統的不確定性和干擾可以被及時估計和補償，這有利于反饋控制提高調節能力。

三電平逆變器可以產生27個電壓矢量，其中對中點電壓能產生影響的是小矢量和中矢量，小矢量又可以分為正小矢量和負小矢量，這兩種小矢量對中點電壓的影響是恰好相反的，正負小矢量的中點電流如表2所示。本文通過調整正負小矢量的作用時間，抵消正負小矢量對中點電壓的影響，以平衡中點電壓。

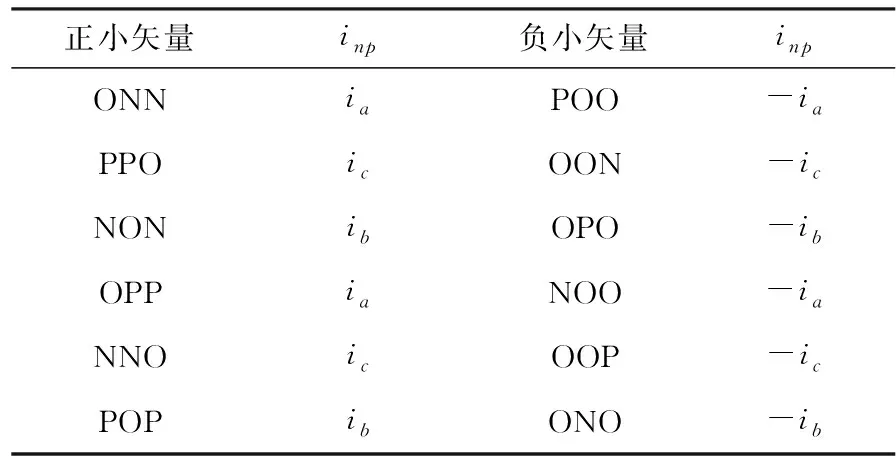
表2 小矢量對應的中點電流

通過引入時間因子k，令負小矢量的作用時間為(1+k)T1/2，那么相應的正小矢量的作用時間為(1-k)T1/2。給中點電壓設置一定的滯環區間[-d,d]，當中點電壓超出該區間時，通過改變k值來調整正負小矢量的作用時間，抵消正負小矢量對中點電壓的影響，以此達到平衡中點電壓的目的。且由于在位置穩定的時候，中點電壓的大小主要是由電容值的對稱性決定的，為了簡化計算量，沒有采用復雜的控制算法。

3 仿真研究

本文用MATLAB/Simulink仿真工具搭建了擺臂結構控制系統，以驗證控制方法的可行性。在仿真工具中搭建的控制系統參數：永磁同步電機的額定功率為750 W，額定轉矩為2.39 N·m，額定電流為3 A，額定轉速為3 000 r/min，峰值轉矩為7.17 N·m，峰值電流為7.2 A，電機磁鏈為0.111 Wb，線電阻1.3 Ω，線電感7.5 mH，轉子轉動慣量為2.7×104kg·m2，電源電壓為150 V(DC)，直流側兩個電容容值均為500 μF。

本文的仿真研究主要分為兩個部分：第一部分是通過對PI，MPC以及MPC + ESO三種算法的位置和速度曲線進行對比，驗證MPC+ESO控制算法的有效性；第二部分是對MPC+ESO控制算法下的中點電壓進行監測，驗證滯環控制對中點電壓的平衡效果。

圖6為指定位置為90°時，采用速度環PI控制算法得到的位置和速度曲線。此時，位置環Kp=50，Ki=0，速度環Kp=1.5，Ki=12。不難看出，在該算法下，電機的到位情況比較差，實際位置和位置指令之間存在1.7°左右的穩態誤差，且相應的，實際轉速和轉速指令之間一直存在1.5 r/min的轉速誤差，試圖把電機的位置提到指令位置。

圖6 PI的位置和速度曲線

圖7為指定位置為90°時，采用MPC控制算法的情況下，得到的位置和速度曲線。可以看出，與圖6的PI算法對比，MPC算法的到位時間T為1.2 s左右，而PI算法為1.8 s左右，MPC算法的到位更快，提升了系統的動態性能。

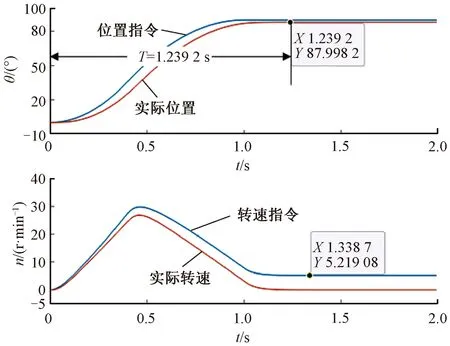
圖7 MPC的位置和速度曲線

圖8為指定位置為90°時，采用MPC+ESO控制算法的情況下，得到的位置和速度曲線。與圖6的PI算法對比可以看出，MPC+ESO的控制算法不僅在到位精度上消除了穩態誤差，且速度跟蹤效果在整個控制過程中都比較好。與圖7的MPC算法對比可以看出，在使用ESO估計系統擾動的情況下，MPC算法提高了到位精度，幾乎不存在穩態誤差。速度跟蹤的效果也變好了，實際轉速和轉速指令之間的誤差被消除了。

圖8 MPC+ESO的位置和速度曲線

圖9為MPC+ESO控制算法下的中點電壓。理想情況下，當直流側兩個電容的容值完全相等時，可以看到，通過滯環控制，中點電壓被平衡在0左右，可以保證逆變器的正常運行。但是在實際情況中，直流側兩個電容的容值不可能保證完全相等。因此在仿真工具中更改一個直流側電容的容值以模擬真實情況，得到容值不相等時的中點電壓曲線。可以看出，當兩個電容的容值不相等時，中點電壓會存在恒定偏置。

圖9 MPC+ESO的中點電壓

4 實驗驗證

本文搭建了由永磁同步電機構成的實驗平臺，驗證控制方法的可行性和性能，實驗平臺如圖10所示。

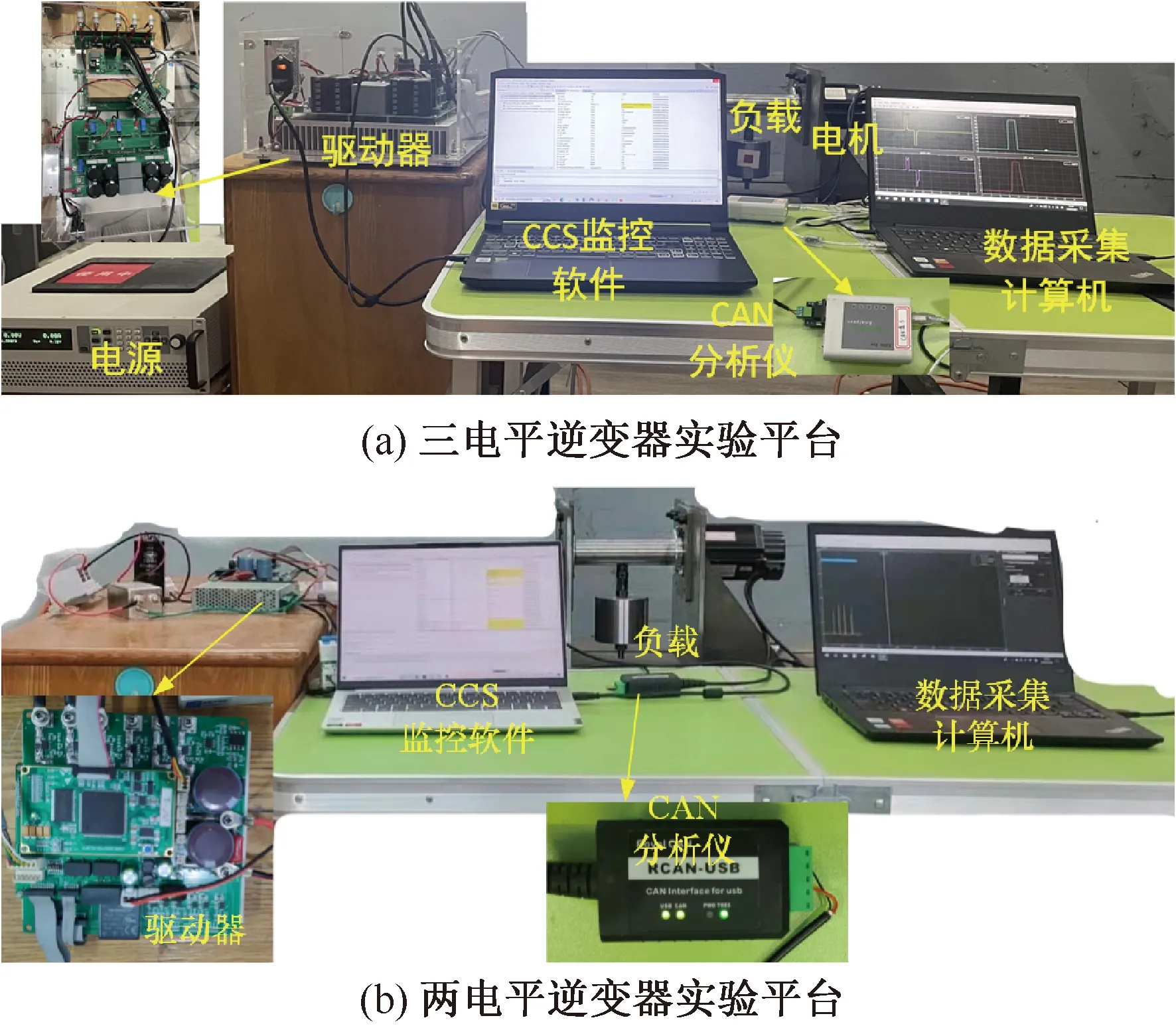
圖10 電機控制系統實驗平臺

實驗平臺主要由以下幾個部分組成：電機、負載、電源、CCS監控軟件、驅動器、數據采集計算機。其中驅動器為基于TI公司的數字處理器芯片TMS320F283789設計的硬件平臺，轉子的實際位置通過16位旋變解碼芯片反饋給驅動器。圖10(a)為三電平逆變器驅動的實驗平臺，采用的IGBT型號為Infineon公司的F3L75R07W2E3_B11。圖10(b)為兩電平逆變器驅動的實驗平臺，采用的IGBT型號為Infineon公司的FS50R07W1E3_B11A。使用CAN分析儀對實驗過程中實驗平臺的各項參數進行采集，并在MATLAB/Simulink仿真平臺中搭建虛擬示波器，對采集到的數據進行更直觀的顯示。

實驗中直接驅動負載使用的永磁同步電機，其參數和仿真設定的一致。本文的實驗驗證分為三個部分：第一部分通過給定位置指令90°，讓負載從0運動到90°，觀察電機的到位精度以及速度跟蹤情況；第二部分通過給定位置指令1 800°，讓電機驅動負載轉動5圈，觀察算法的可靠性和穩定性；第三部分為對比兩電平逆變器驅動和三電平逆變器驅動情況下的電流諧波分量。

圖11為采用PI控制的到位精度測試。此時，位置環Kp=50，Ki=0，速度環Kp=1.5，Ki=12。從圖11(a)的位置曲線可以看出，PI控制算法在到位的過程中，電機實際位置與指令位置之間存在0.2°左右的誤差。觀察圖11(a)的速度曲線可以看到，電機的實際轉速和轉速指令之間一直存在較大誤差，說明轉速動態響應速度較慢，影響了電機的到位精度。圖11(b)是采用PI控制時的電流和NPC三電平逆變器的中點電壓。可以看到，電流的響應速度較快，且中點電壓由于直流側兩個電容容值不相等，導致存在8 V左右的恒定偏置，屬于合理范圍內。

圖11 采用PI控制的到位精度測試

圖12為采用MPC控制的到位精度測試。對比圖11(a)和圖12(a)的位置曲線可以看出，MPC控制算法相比較于PI控制算法，提高了系統的動態性能，縮短了電機的到位時間。但是在到位精度上，MPC控制算法存在1°的穩態誤差。從圖12(a)的速度曲線可以看出，實際轉速雖然在運動初期跟蹤轉速指令的效果很好，但是位置環存在穩態誤差，導致最后實際轉速與轉速指令之間存在7.5°左右的轉速誤差。圖12(b)是采用MPC控制時的電流和NPC三電平逆變器的中點電壓，擺臂是個負載時變結構，在運動過程中，電流曲線存在比較小的振蕩。

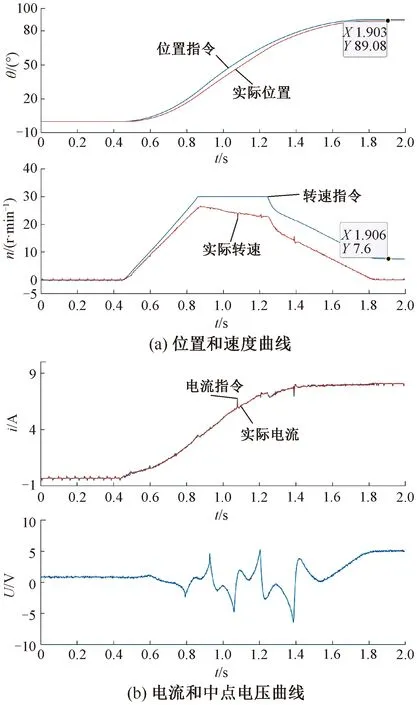
圖12 采用MPC控制的到位精度測試

圖13為采用MPC+ESO控制的到位精度測試。對比圖13(a)和圖11(a)的位置曲線可以看出，MPC + ESO控制算法與PI控制算法相比較，MPC + ESO提高了系統的動態性能，縮短了電機的到位時間。對比圖13(a)和圖12(a)的速度曲線可以看出，采用MPC + ESO的控制算法，在加入ESO來估計系統擾動，并且在速度控制器中引入了對干擾的前饋補償部分的情況下，電機的實際速度在整個運動過程中跟蹤轉速指令的效果都很好。在電機驅動系統中，速度環是位置環的內環，內環能決定外環的控制效果，因此對比位置曲線可以看出，速度跟蹤的精度提高后，位置跟蹤的精度也對應提高了，系統的穩態誤差被消除了，到位誤差只有0.01°，幾乎可以忽略不計。

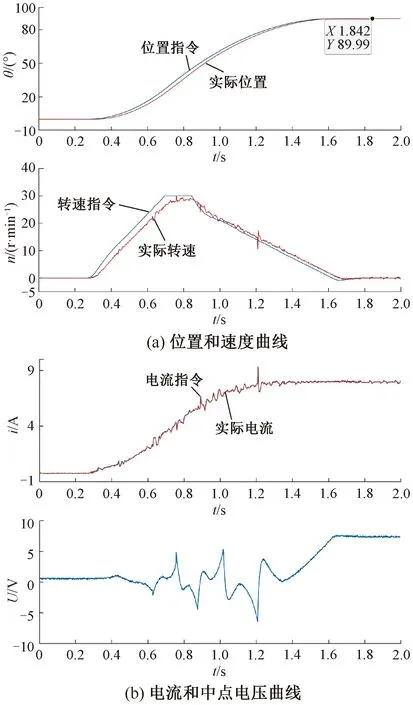
圖13 采用MPC+ESO控制的到位精度測試

圖14為采用MPC + ESO控制的穩定性實驗。在該組實驗中，通過給定1 800°的位置指令，使電機驅動擺臂結構轉動5圈，來觀察系統在重復運動過程中的穩定程度。從圖14的速度曲線可以看出，電機的實際轉速在轉速指令曲線附近有小幅度的振蕩。且從電流曲線可以看出，在運動5圈的過程中，電流以正弦波的方式周期性變化。不難看出，MPC+ESO控制算法的可靠性和穩定性可以得到保證。

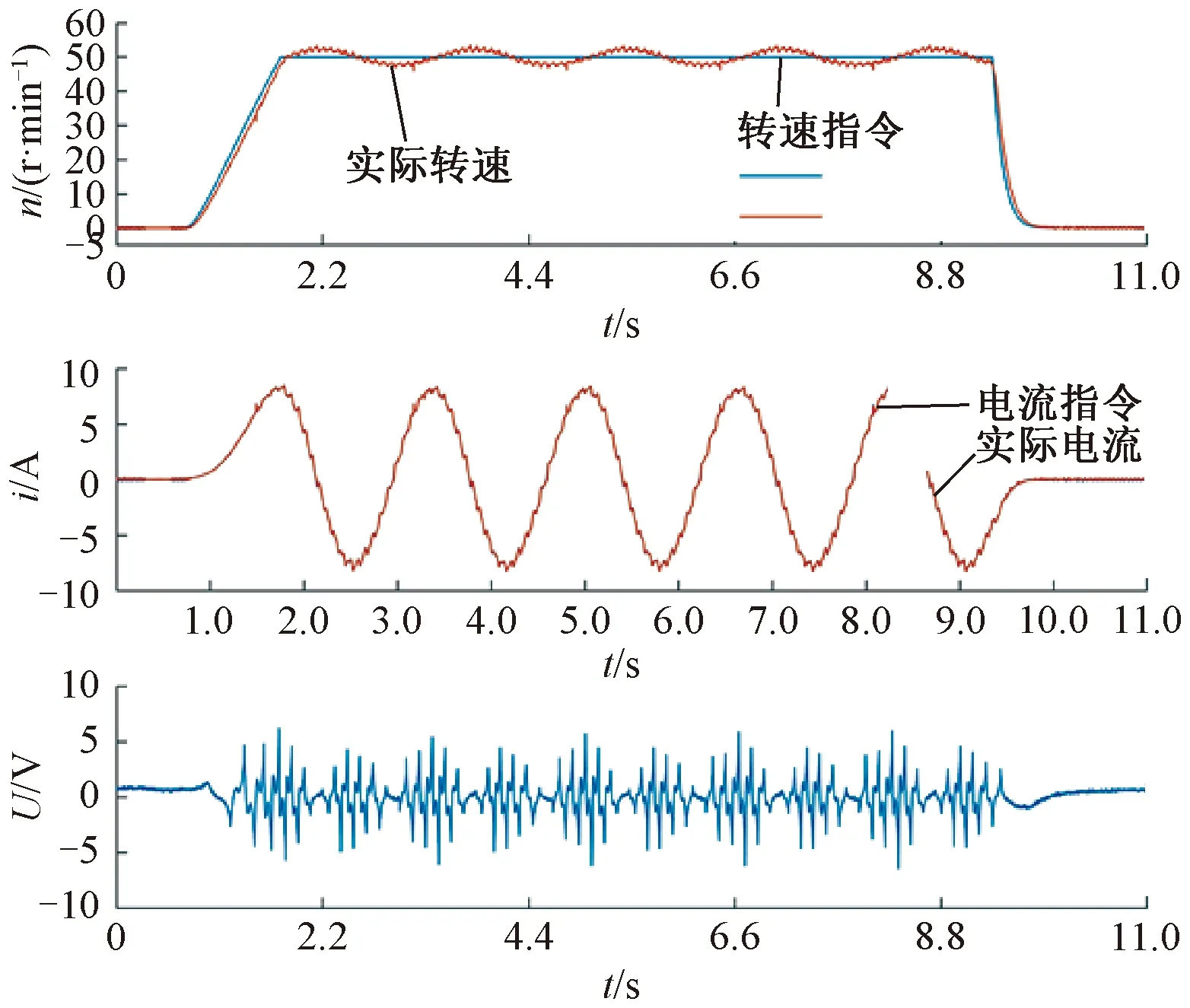
圖14 采用MPC+ESO控制的穩定性測試

圖15和圖16為兩電平逆變器驅動和三電平逆變器驅動的相電流及其所對應的FFT曲線。

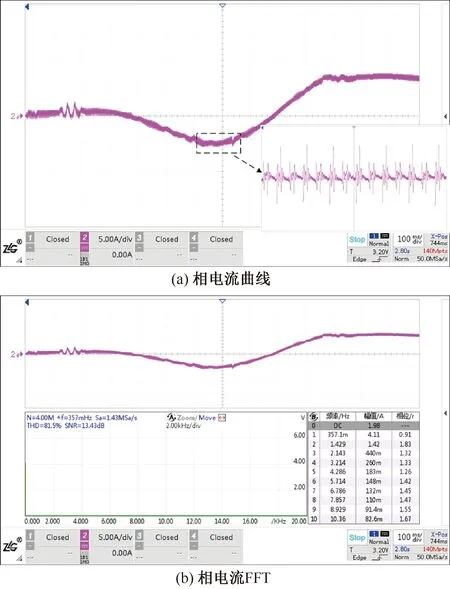
圖16 三電平的相電流和相電流FFT曲線

對比圖15(a)和圖16(a)可以看出，三電平逆變器驅動的定子電流紋波噪聲更小，三電平逆變器的高頻信號諧波更小。對比圖15(b)和圖16(b)可以更加直觀地看出，三電平的電流諧波幅值更小。

5 結 語

本文針對大慣量的擺臂結構，采用NPC三電平逆變器驅動，以減小電流諧波，且采用滯環控制來平衡中點電壓。針對傳統的PI控制算法動態性能差的問題，在速度環中加入MPC算法提高系統的動態性能和魯棒性。引入了ESO來估計集中擾動，并在速度環MPC中添加了基于估計擾動的前饋補償項，改善了當系統存在強干擾的情況下MPC的控制效果。仿真和實驗驗證了本算法的有效性和穩定性。