基于響應面法和粒子群算法的橋梁高聳臨時提升支架優化

占玉林，許江輝，許 俊，邵俊虎，林智敏，何 鵬

（1.西南交通大學 土木工程學院，四川 成都 610031；2.中鐵第四勘察設計院集團有限公司，湖北 武漢 430063；3.成都大學 建筑與土木工程學院，四川 成都 610106；4.中鐵上海工程局集團第五工程有限公司，廣西 南寧 530200）

鋼拱橋具有造型美觀、跨越能力大、施工方式靈活等突出優點，使其在橋梁建設領域中得到廣泛應用。常見的鋼拱橋形式有鋼管混凝土拱橋、鋼箱拱橋等［1-3］。其施工方法大致分為：支架施工法、懸臂拼裝法、轉體施工法以及纜索吊裝法等［4-6］。支架整體提升方法屬于支架施工法的1種，起初應用于建筑領域，隨著整體提升技術的不斷成熟，其憑借著拼裝精度高、結構整體性好和施工安全可靠等優點在大跨徑拱橋施工中逐漸得到推廣應用［7-8］。拱肋整體提升支架作為大跨徑拱橋進行安全吊裝施工的重要結構，其在施工過程中受力復雜，強度和穩定性問題十分突出。若支架尺寸過小，會造成結構的強度和穩定性降低，危及施工安全；而支架尺寸過大，則其利用率較低，增加工程造價［9-10］。目前，提升支架的設計計算理論尚不完善，在確定提升支架結構參數時，需綜合考慮其安全性和經濟性［11］。

目前，大量學者通過響應面法［12-14］對結構優化設計進行了廣泛研究。徐征杰等［15］通過構建響應面函數獲得強風化花崗巖地層在不同盾構推進速度下的最優改良參數；成棣等［16］研究了多項式響應面優化方法和高斯徑向基函數響應面優化方法對于車輪踏面的優化效果，發現響應面方法適用于車輪踏面優化，優化后的車輪踏面磨耗指數降低明顯；宗周紅等［17］基于響應面方法成功對大跨徑連續剛構橋健康監測有限元模型進行了修正，模型優化后計算得到的頻率跟實測頻率較吻合。Ren等［18］將響應面法應用于土木工程結構的結構動力學中，通過仿真數據構建二次多項式響應面，并通過簡支梁和預制連續梁驗證了模型的準確性，與傳統方法相比，該法高效且易收斂。

雖然上述學者通過理論分析、數值計算等方式對結構進行了優化，但實際工程中結構各優化目標參數的隨優化設計參數的變化規律往往并不統一，且可能相互沖突，協調其關系，實現結構的最優化有待研究。

本文針對橋梁高聳臨時提升支架（以下簡稱“提升支架”），建立相應的數值模型，在運用響應面法求得提升支架各優化目標參數響應面函數的基礎上，構建提升支架的目標優化函數，采用粒子群優化算法尋找最優解，得到提升支架的合理結構形式。

1 基于響應面法和粒子群算法優化的基本原理

針對工程結構優化，本文提出一種基于響應面法和粒子群算法的優化方法，其基本流程如圖1所示。

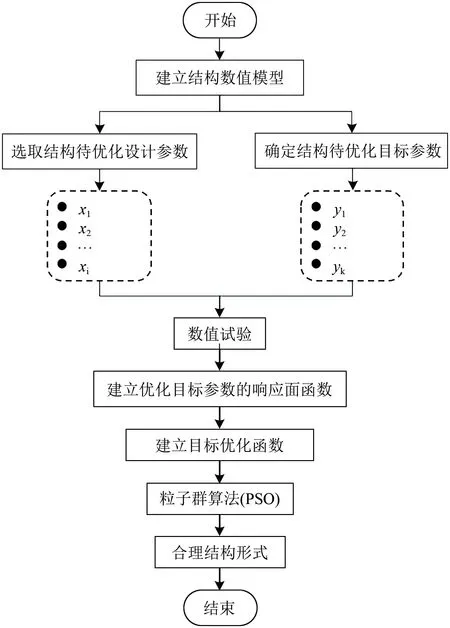
圖1 工程結構優化流程圖

1.1 響應面法基本原理

響應面法（Response Surface Method，RSM）由Box 等［19］于1951 年提出，是一種構建近似函數的方法。利用響應面法構造近似函數時，首先要確定近似函數的形式，然后運用統計試驗設計方法在空間內選取足夠多的樣本，最后運用最小二乘法原理擬合試驗設計樣本的分析結果得到響應面函數。通常響應面函數采用二階函數形式，即

式中：xi為設計參數；a0，bi和ci為待定系數，需由試驗樣本進行確定；n為設計參數個數。

響應面函數的待定系數向量A可由下式計算

式中：Y為響應面函數預測向量；X為優化參數矩陣；m為求解待定系數所需試驗樣本數量。

1.2 目標優化函數

與單目標優化問題不同，由于多目標優化問題（Multi-objective Optimization Problem，MOP）［20-21］中的各個子優化目標間可能相互沖突，無法令所有優化目標參數均達到最優解，因此，需要尋找一組使所有優化目標函數盡可能達到最優的設計參數值。為獲得最優解，本文基于多個優化目標函數，將多目標優化問題轉變為單目標優化問題，考慮到各參數的量綱不同，為了便于統一求解，對各目標優化函數進行無量綱化處理，即

式中：yi為第i個目標優化函數；yimax和yimin分別為yi的極大值和極小值。

則目標優化函數Y可表示為

式中：ki為各優化目標參數的權重系數。

1.3 粒子群優化算法原理

粒子群算法（Particle Swarm Optimization，PSO）是由Eberhart和Kennedy于1995年首次提出用于解決全局優化問題的智能算法［22］。粒子群算法將粒子視為沒有體積和質量的點，并為每個粒子設置速度和位置2 個參數。每個粒子以自身的最佳位置作為局部最優目標，以種群歷史的最優位置為全局最優目標，在空間中進行運動［23-25］。每個粒子代表解空間的1個候選解，解的優劣度由適應度函數決定，本文中適應度函數為目標優化函數Y。粒子群算法的進化方程為

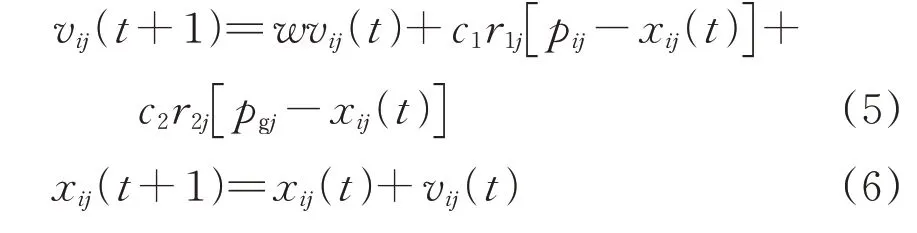
式中：i為粒子編號；j為粒子所處空間的位置；t為粒子迭代次數；vij為粒子速度；xij為粒子位置；pij為粒子i在第j維的最優位置；pgj為全部粒子在第j維空間的最優位置；w為慣性權重系數［26］；c1和c2為學習因子，取值范圍為1～2.5［19］；r1j和r2j為相互獨立的0～1之間的隨機數。

2 橋梁高聳臨時提升支架優化目標函數

某大跨徑提籃式鋼箱拱橋在施工過程中，中拱段采用低位拼裝+高聳門式支架整體提升，如圖2所示。提升支架為高87.5 m的鋼結構，鋼管材料采用Q235 級鋼材，并由焊接拼裝制成。其中，承臺以上13.6 m范圍內，采用鋼管混凝土，其余部分采用空心鋼管，支架由立柱與橫撐組成，立柱鋼管直徑為1 520 mm。由于提升支架高度高、提升重量大，提升過程安全風險大，且造價高，為使得其兼顧受力性能與造價，對提升支架結構進行優化。

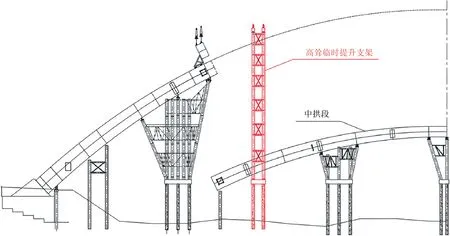
圖2 橋梁高聳臨時提升支架整體提升現場施工示意圖

2.1 優化設計參數和優化目標參數選取

提升支架作為拱肋提升過程中的主要承重結構，對結構強度和穩定性要求較高，需保證其在拱肋提升過程中的受力和變形的安全性［27］。因此，選取鋼管混凝土立柱內混凝土填充高度x1、鋼管外徑x2和鋼管壁厚x33個對提升支架結構性能影響較大的因素為優化設計參數，其原始設計值分別為：x1初=13.6 m，x2初=1 520 mm，x3初=16 mm。充分考慮提升支架的尺寸設計要求和實際情況，優化參數x1、x2和x3的上下限取值分別為［0，27］m，［1 000，2 000］mm 和［10，22］mm。在保證提升支架結構受力性能的同時，還應考慮經濟性要求，因此選取最大拉應力y1、最大壓應力y2、屈曲系數y3和工程造價y4作為提升支架的優化目標參數。

2.2 響應面函數建立

上述提升支架4 個優化目標參數的優化設計參數均為3個，因此4 個優化目標參數的響應面函數的形式為

由式（7）可見，4 個優化目標參數響應面函數的待定系數均為7個，至少需進行7 次試驗建立各優化目標參數的響應面函數。

為了求解優化目標參數的響應面函數，依據提升支架結構參數，運用有限元分析軟件MIDASCIVIL，建立圖3 所示的橋梁高聳臨時提升支架數值模型。各構件均采用梁單元模擬，柱頂鋼箱梁選取Q345 鋼材，鋼管立柱選取Q235 鋼材，承臺及鋼管內灌注混凝土選取C30混凝土材料。樁基底部采用固結邊界條件，上部鋼結構與承臺間采用剛性連接。施工過程中拱肋的重量以集中力的方式施加在支架頂部的鋼箱梁上。

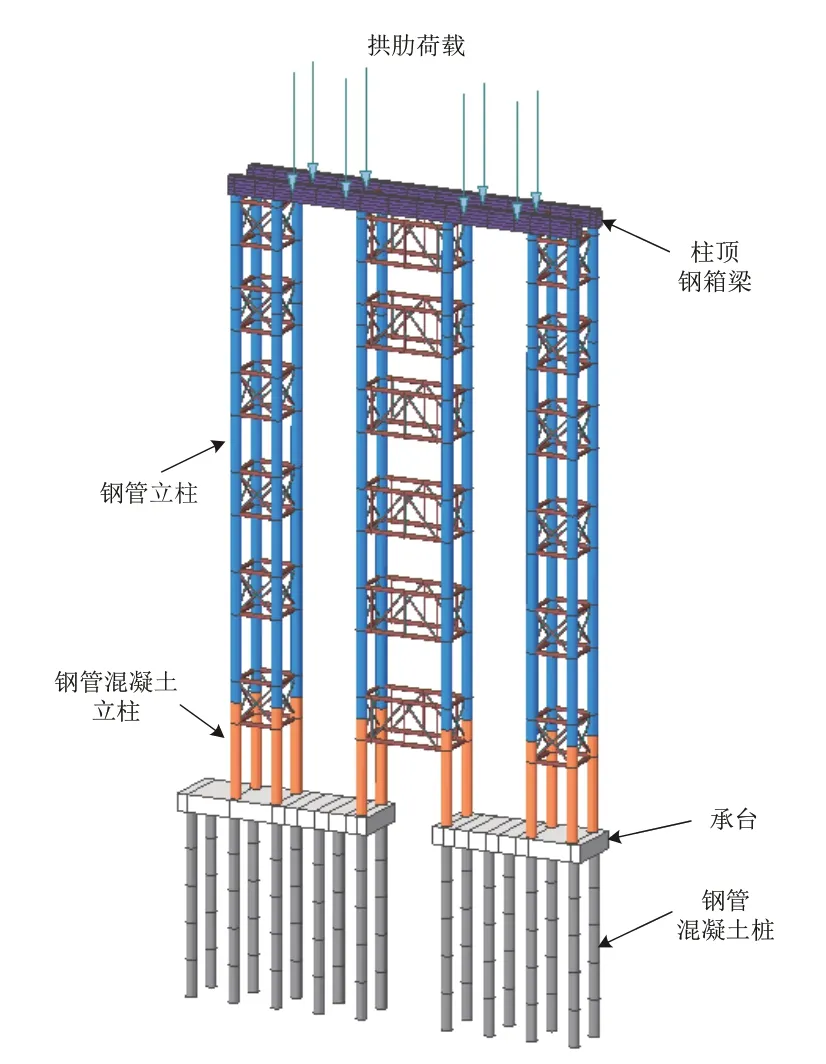
圖3 橋梁高聳臨時提升支架有限元模型

為保證響應面函數的精確性并驗證其擬合效果，改變數值模型中的優化設計參數，共進行19組試驗，數值模擬結果見表1。

根據響應面法的基本原理，對表1 中的計算結果進行多元回歸擬合，得到提升支架最大拉應力y1、最大壓應力y2、屈曲系數y3及工程造價y4這4個優化目標參數響應面函數的待定系數的取值，見表2。

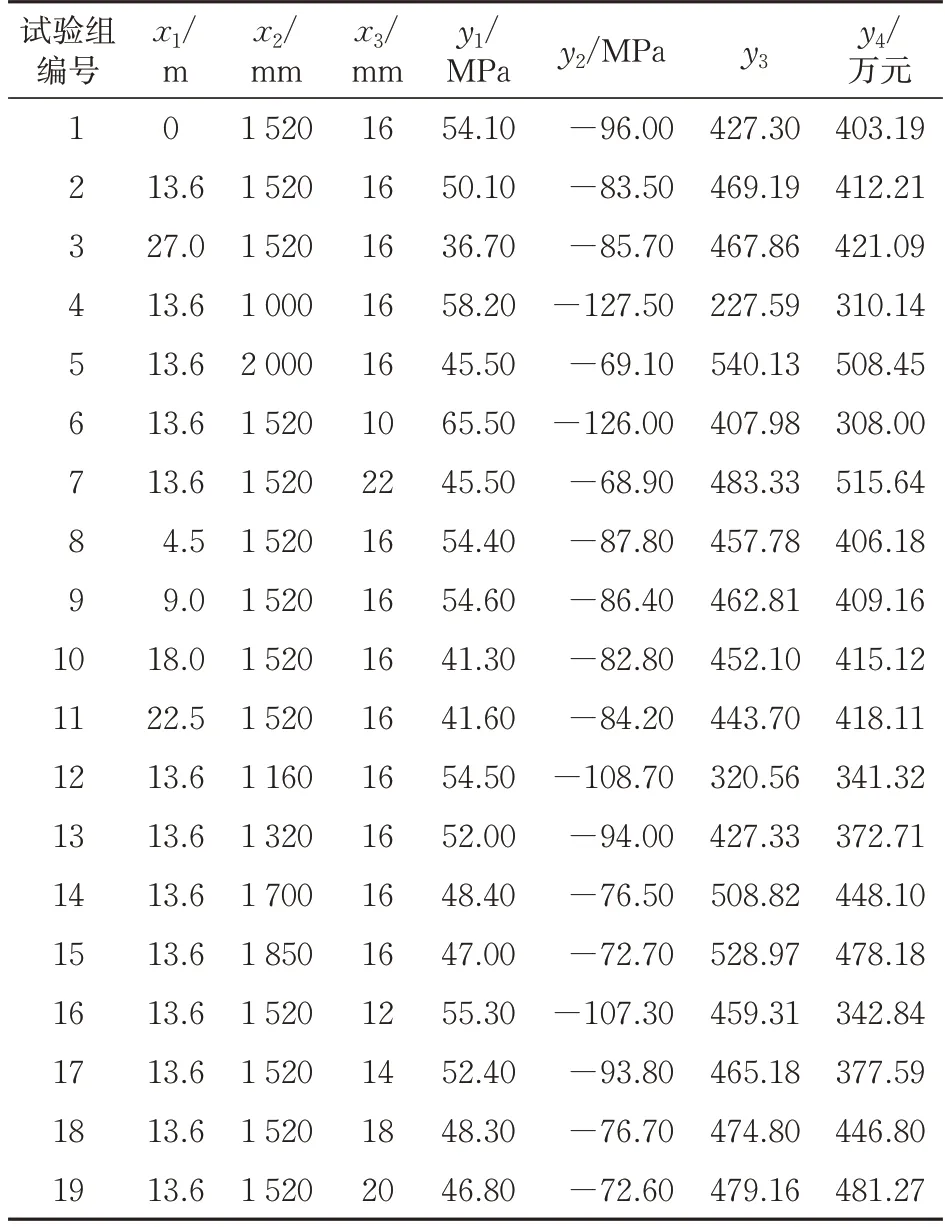
表1 提升支架數值模擬結果

表2 優化目標參數的響應面函數系數取值

為驗證響應面函數的準確性以及預測能力，通過回歸分析判斷其擬合度。判定系數R2表示響應面函數擬合值與計算值之間的差異程度，在0～1之間取值，其值越大，則響應面函數擬合就越接近實際情況；相對均方根誤差Re表示響應面函數的精度，其值越小，表示響應面函數的精度越高。響應面函數的擬合度分析結果見表3。

表3 響應面函數擬合度量值

由表3 可知，各響應面函數的判定系數均接近1，且相對均方根誤差很小，由此驗證了各響應面函數的擬合效果較好，可用于結構優化。

2.3 目標優化函數

為了構造目標優化函數Y，首先根據式（3），對4個優化目標參數的響應面函數進行無量綱化處理，得到考慮到提升支架對結構安全性和經濟性的不同設計需求，引入了2 個權重系數，即安全系數α和成本系數β。則得到目標優化函數，即

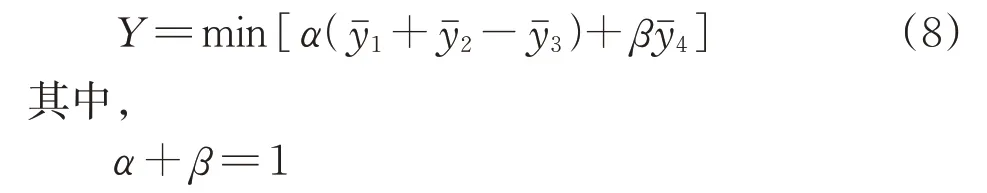
當α＜β時，表示在結構滿足正常使用和極限承載能力的前提下，比較注重結構的經濟性；當α=β時，表示在結構設計中安全性和經濟性同等重要；當α＞β時，表示在結構設計中相較結構的經濟性，結構的安全性更應受到關注。

3 橋梁高聳臨時提升支架優化

基于上述各優化目標參數的響應面函數及目標優化函數，根據粒子群算法的基本原理，利用MATLAB 軟件編制相關優化程序進行尋優分析。粒子數目取值為40，學習因子c1和c2取值均為2，慣性權重系數w取值為0.5，最大迭代次數取為1 000，3 個自變量x1，x2和x3的取值范圍分別取為［0，27］m，［1 000，2 000］mm和［10，22］mm。

由于單次尋優的結果具有一定的隨機性，因此α與β取不同值，對目標優化函數進行多次優化，取優化的平均值作為最終的優化結果。α和β在不同取值情況下，各優化目標參數的計算結果見表4。

表4 不同α和β組合下各優化目標參數值

當α=0.1 或α=0.2時，結構最優優化設計參數得到造價雖然較低，但結構的最大壓應力過大，安全儲備小，因此過于重視結構造價而降低結構安全性是不合理的。

當α=0.3 或α=0.4時，結構的屈曲系數較大，但其不是控制結構安全性的主要參數，同時最大拉應力較小，最大壓應力較大，結構的強度主要由最大壓應力控制，最大壓應力分別為90 和71 MPa，結構的安全儲備較大，當α由0.3 變為0.4時，造價增高19.4%。

當α取0.5～0.9（對應的β取0.5～0.1）時，結構的最大拉應力、最大壓應力、屈曲系數在數值上變化不大，且結構均處于較低應力水平，材料得不到充分利用，對應的造價逐漸增高，α=0.5和α=0.9時優化所得到的造價相差71.46 萬元，這說明在本工程結構中，當α從0.5逐漸增加至0.9時，成本系數與安全系數的取值對優化結果的影響相對比較小。

綜合上述對安全系數α和成本系數β的討論可知，當α取為0.3左右，β取為0.7左右，結構具有一定的安全儲備，同時兼顧了造價的經濟性，4 個目標優化參數的優化結果能夠達到相對理想的平衡。需要說明，當α取為0.3，β取為0.7時并不是絕對意義上的最優解，而是多目標優化函數Pareto前沿解集中的1個非支配解，在求該非支配解的過程中綜合考慮了結構的強度、穩定性和工程造價等多個目標優化函數，它是在滿足各目標優化函數取得平衡狀態下的綜合較優解。

優化前后提升支架的各響應面函數值如圖4 所示。由圖4可知：優化后提升支架的最大拉應力由50.1 MPa降低為38.6 MPa，減小幅度為23%；最大壓應力由83.5 MPa 增加至90.47 MPa，增加8.3%；屈曲系數優化前后變化較小；工程造價由412.21 萬元減少至405.76 萬元，降低幅度為1.6%。分析結果表明，在支架最大壓應力和屈曲系數變化不大的情況下，結構最大拉應力明顯降低，安全度得到較大提升，此外，工程造價還能略微降低，優化效果比較可靠。

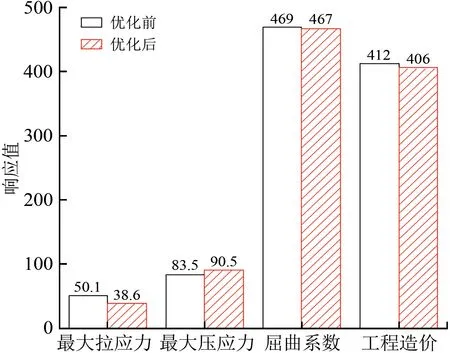
圖4 優化效果對比

4 結論

（1）本文提出的響應面法和粒子群算法相結合的多目標優化方法能有效進行提升支架的設計優化。

（2）提升支架結構優化目標參數的響應面函數擬合精度較高，響應面函數可合理構建結構優化參數與優化目標參數之間的數學關系。

（3）通過引入權重系數可將工程中的多目標優化問題轉變為單目標優化問題，為解決多個優化目標之間存在矛盾的情況提供了解決方法。

（4）當安全系數和成本系數分別取0.3 和0.7時，提升支架的多目標優化函數得到較優解，優化后在支架最大壓應力和屈曲系數變化不大的情況下，結構最大拉應力明顯降低（降幅達23%），安全度得到較大提升，此外，工程造價還能略微降低，優化效果顯著。