鐵路新型柱
--板組合式高墩模擬及地震易損性研究

王 力，虞廬松，李子奇，王 嘉，李健寧

（1.蘭州交通大學 土木工程學院，甘肅蘭州 730070；2.蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，甘肅蘭州 730070）

近年來，我國交通事業在西部地區發展迅速，橋梁以其優異的跨越能力在西部交通線路廣泛使用。據統計，西部交通線路上墩高高于40 m 的橋梁超過橋梁總數的40%［1］，其中，包含大量超出規范適用范圍的鐵路高墩大跨連續剛構橋。

鐵路橋梁作為生命線工程，一旦在地震中遭受嚴重破壞造成線路中斷，短時間內將難以修復，勢必引起更大的經濟損失。國內外學者針對不同截面型式的鐵路高墩抗震問題已進行了廣泛研究。橋墩構件主要為矩形［2-3］、圓形［4］和圓端形［5］空心截面。盧三平［6］對矩形空心高墩連續剛構橋的抗震性能進行了討論。周長東等［4］對圓形空心高墩進行地震易損性的分析表明，墩頂、墩底和墩中部均為易損部位，且墩底較墩頂、墩中部更易損。SHAO 等［5］通過圓端形空心高墩振動臺試驗發現，該類高墩震損模式與其擬靜力試驗結果差異顯著，設計中應考慮高階振型對其損傷模式的影響。韓國慶等［7］的試驗研究發現圓端形空心橋墩以彎曲破壞為主，墩底實心與空心過渡段截面為受力最不利位置。此外，學者們還從場地效應［8］、地震動特性［9］和減隔震［10］等方面對鐵路高墩橋梁的抗震性能開展了大量研究。

2003年，Bruneau等［11］首次提出了震后不修復或稍做修復即可投入使用的功能可恢復抗震結構的概念。太平洋地震工程研究中心（PEER）將功能可恢復抗震結構理念認定為下一代基于性能的地震工程的核心。目前，可恢復功能抗震結構［12］主要有自復位結構、搖擺結構、框架-剪力墻結構和帶可更換構件結構等多種形式。基于可恢復功能抗震結構理念，我國黃-韓-侯鐵路縱目溝高墩大跨連續剛構橋主墩首次采用新型柱-板組合式空心高墩，該墩柱間板在正常營運階段為橋梁整體結構提供縱、橫向剛度，而在地震中作為犧牲構件保護墩柱的安全性，震后也可通過簡單修復實現橋梁功能快速恢復。該新型墩設計理念先進，具備較好的應用推廣價值，但該新型結構設計方法及其在地震作用下的損傷機制、破壞模式等方面還有待進一步研究。

基于此，本文以縱目溝特大橋為背景，提出采用多垂直桿元模型模擬柱間板、纖維梁單元模擬墩柱及墩上橫梁的新型柱-板組合式高墩的有限元模擬方法，建立全橋非線性有限元模型并進行地震易損性分析，探究該新型高墩的抗震性能，以期為該新型結構的抗震設計和應用推廣提供必要參考。

1 工程概況

縱目溝特大橋為（78+2×136+78）m 預應力混凝土連續剛構橋，如圖1所示。梁高5～10 m，按1.8次拋物線變化；主墩（5#墩）為新型柱-板組合式空心高墩，墩高105 m。該橋墩是基于框架-剪力墻結構抗震設計思路提出的一種新型組合式結構，主要由4根墩柱、柱間混凝土板和橫梁組成，其抗震理念為柱間板在正常使用階段為結構提供較大的剛度，通過自身強度抵抗中小震作用，而在大震作用下通過柱間板的開裂破壞避免或減輕墩柱的損傷。

圖1 縱目溝特大橋現場圖

主墩墩頂實心段采用C55混凝土，其余位置均采用C50混凝土。主墩墩身構造和典型截面配筋如圖2所示。

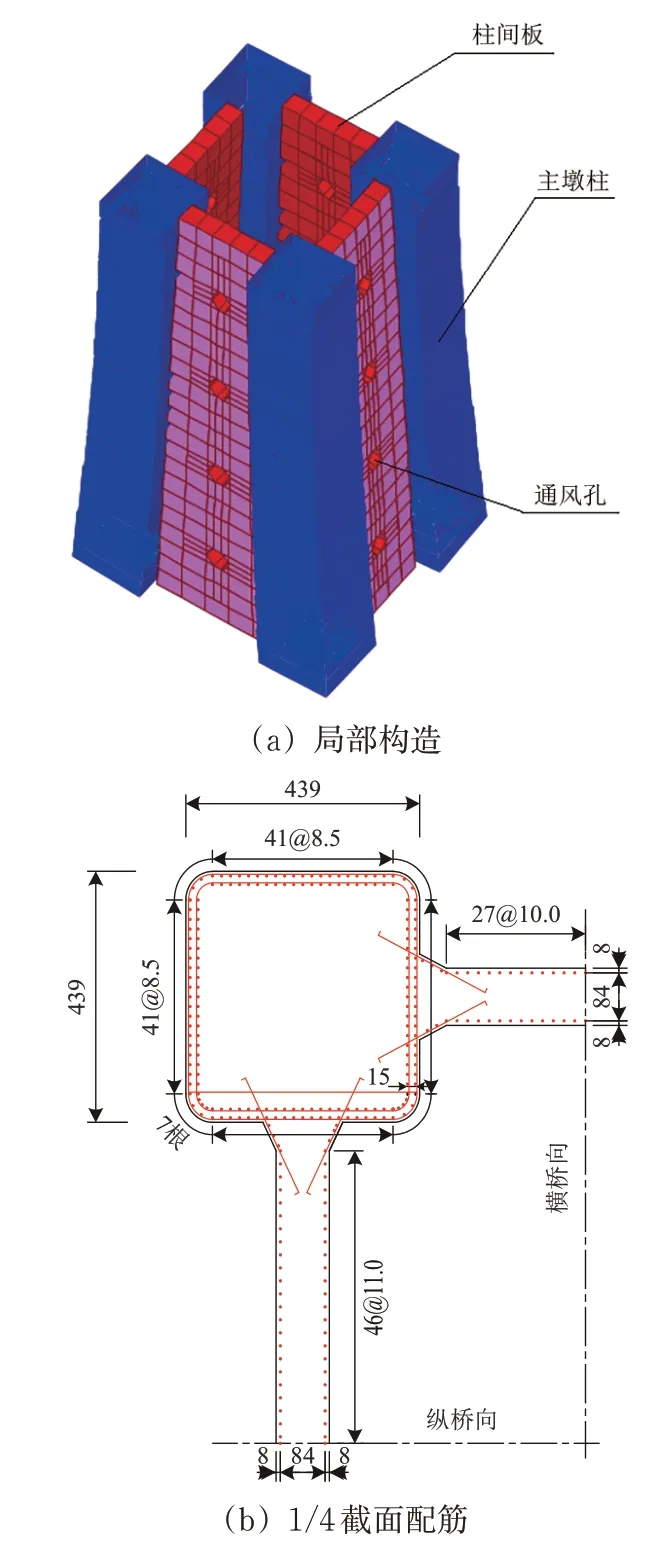
圖2 主墩構造及配筋（單位：cm）

2 新型柱-板組合式高墩模擬

對于新型柱-板組合式空心高墩組合結構，采用實體單元模擬能夠較好地揭示其地震損傷行為，但建模工作量大、計算耗時長；采用一般梁單元模擬難以得到柱、柱間板的破壞順序及耗能特性。為了解決上述不足，本文采用纖維梁單元模擬墩柱和橫梁、多垂直桿元模型模擬柱間板，建立新型柱-板組合式高墩有限元模型，進行其在地震作用下的耗能機制和損傷發展規律研究。

2.1 柱間板多垂直桿元模型

合理模擬柱間板是該組合結構建模計算的重點。有限元法解決框架剪力墻結構的非線性問題時，常將單元模型分為微觀模型和宏觀模型2 類。微觀模型主要適用于小構件或局部構件的研究，顯然不適用于柱-板組合式空心高墩；宏觀模型是將一段板件作為一個單元等代實際板件的受力特點，可大幅減小計算量。目前，較為實用的宏觀模型有桁架模型、二元件模型、三垂直桿元模型及多垂直桿元模型等。李子奇［13］通過柱板式橋墩擬靜力試驗發現墩柱在地震中以彎曲破壞為主，柱間板以剪切破壞為主。由于二元件模型存在彎曲彈簧滯回關系確定困難的缺點，而多垂直桿元模型可在有效避免二元件模型不足的同時，考慮中性軸的移動，是較為理想的宏觀模型［14］。

柱間板多垂直桿元模型在柱間板上、下混凝土剛性橫梁用n個剛度分別為K1，K2，…，Kn的垂直桿元模擬柱間板的彎曲剛度和軸向剛度，用中心桿元位置處2 個剛臂間的1個剛度為Ks的水平彈簧模擬模擬柱間板剪切剛度，本橋模擬時，根據柱間板的幾何尺寸，取n=4，如圖3 所示。圖中：bs和h分別為柱間板的寬度和高度；r為水平彈簧高度參數，取為0.5。

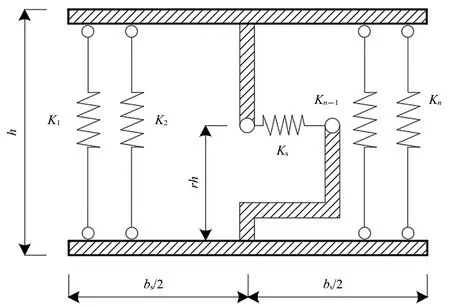
圖3 柱間板多垂直桿元模型

柱間板多垂直桿元模型中，各垂直桿的軸向剛度采用圖4所示的非對稱二折線軸向恢復力骨架曲線計算；水平彈簧剛度采用圖5所示的對稱三折線剪切剛度恢復力骨架曲線計算［15］。圖4 中：Kse和Kce分別為垂直桿受拉、壓彈性剛度；Fsy和Fcy分別為垂直桿受拉和受壓的屈服力；dsy和dcy分別為垂直桿受拉和受壓屈服時的變形；Ksy和Kcy分別為垂直桿屈服后的抗拉、壓剛度。圖5 中：Fv，c和Fv，y分別為柱間板的開裂剪力和屈服剪力；Δc為柱間板混凝土開裂變形；Δy為柱間板鋼筋屈服變形。

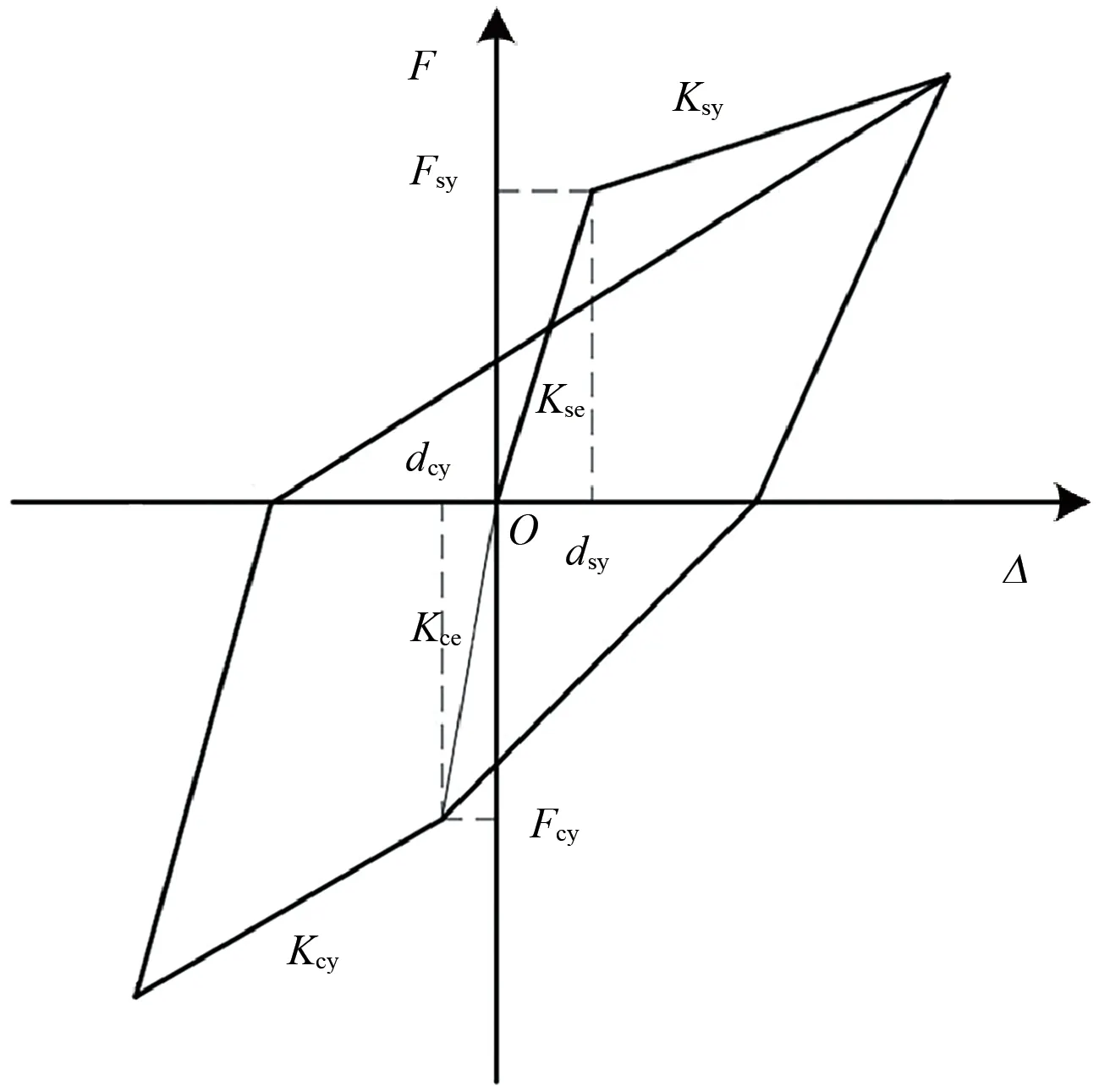
圖4 垂直桿軸向恢復力骨架曲線

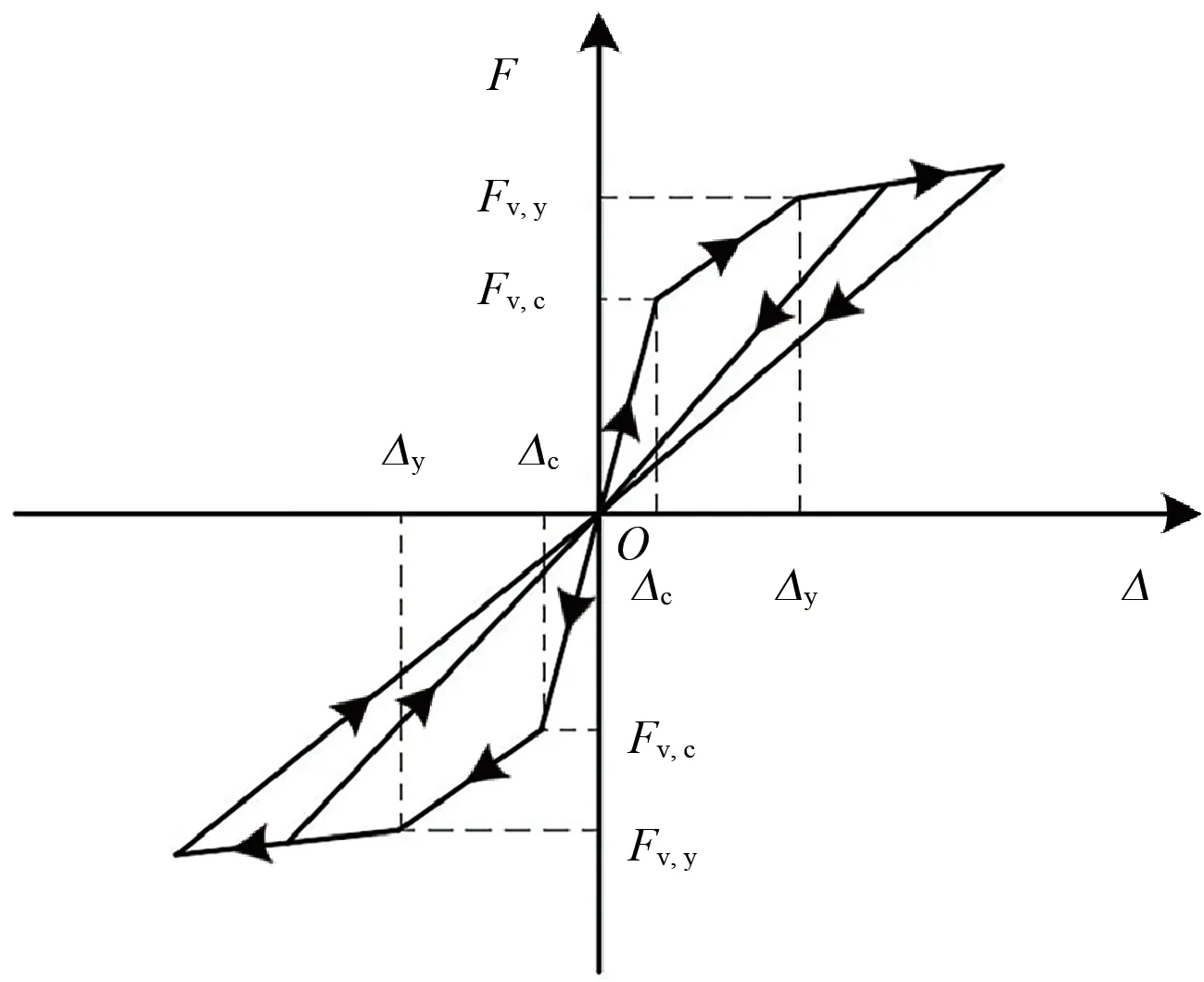
圖5 水平彈簧剛度恢復力骨架曲線

垂直桿受拉彈性剛度和屈服變形按下式計算。

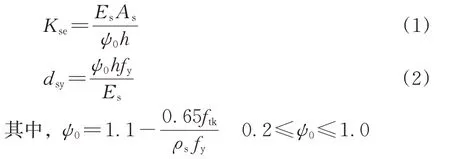
式中：ψ0為應力不均勻系數；ftk為混凝土軸心抗拉強度；fy為鋼筋抗拉強度設計值；ρs為截面配筋率；Es為鋼筋彈性模量；As為垂直桿鋼筋截面積。

當垂直桿受壓時，以混凝土受壓屈服點計算垂直桿彈性剛度和屈服變形，即

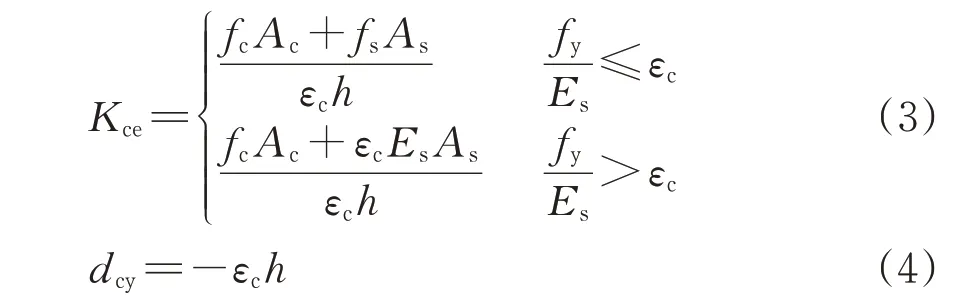
式中：fc和εc分別為混凝土抗壓強度和峰值壓應變，取εc=0.002；Ac為垂直桿混凝土截面積。

依據文獻［15］，垂直桿屈服后抗拉剛度Ksy取0.01Kse，抗壓剛度Kcy取0.02Kce。

柱間板的水平彈簧的初始彈性剪切剛度為

式中：G為混凝土彈性剪切模量；Aw為柱間板截面面積；k為剪切變形的形狀系數，對于矩形截面，一般取k=1.2。

柱間板開裂剪力和屈服剪力分別為

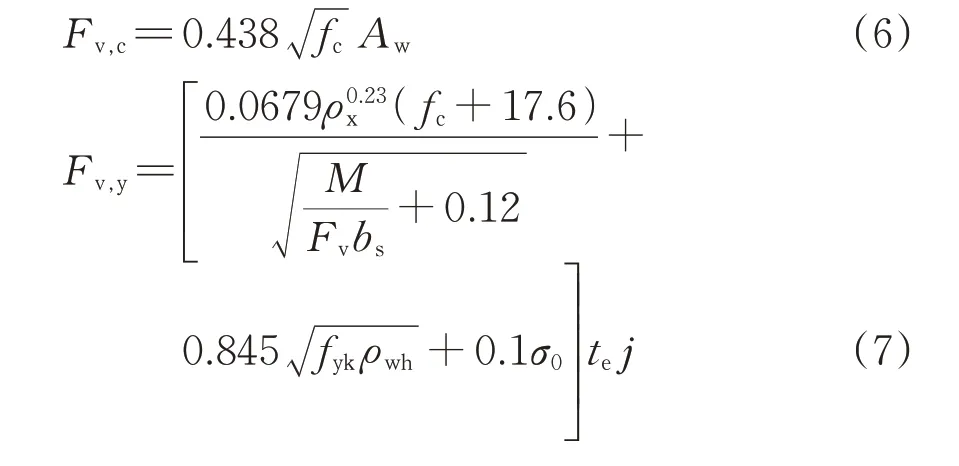
其中，

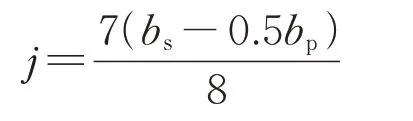
式中：ρx為有效縱筋配筋率；fyk為水平鋼筋屈服強度；M和Fv分別為柱間板所受彎矩和剪力；te為柱間板截面平均厚度；ρwh為柱間板有效水平配筋率；σ0為板截面平均壓應力；bp為單個墩柱的寬度。

柱間板開裂后剪切剛度與初始彈性剪切剛度之比為

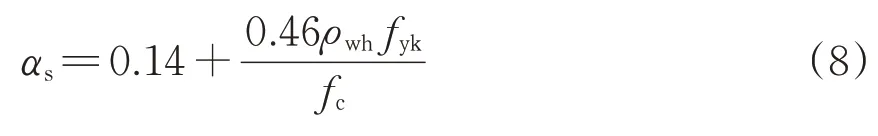
混凝土開裂變形與鋼筋屈服變形為

依據文獻［15］，水平彈簧屈服后剪切剛度取0.002。

2.2 全橋有限元模型

運用MIDAS Civil建立全橋非線性有限元模型。墩柱和墩上橫梁采用非線性纖維梁單元模擬，其中，鋼筋采用Menegotto-Pinto 本構模型，核心混凝土采用Kent-Park 本構模型。次墩和邊墩均采用梁單元模擬，并在各墩頂、底設塑性鉸。4#，5#和6#墩為剛構墩，各墩頂與對應梁底采用剛性連接，邊墩上活動盆式支座采用彈性連接模擬，墩頂、梁底與支座運用豎向剛性連接，剛臂下端與墩頂節點采用另外的剛臂進行連接，剛臂上端與主梁節點剛性主從約束［16］。大量震害表明，橋梁上部梁體在地震作用下發生破壞的概率遠小于橋墩系統［17］，故采用線性梁單元模擬梁體。主梁上部二期恒載為150 kN·m-1。柱間板采用多垂直桿元模型模擬。全橋有限元模型如圖6所示。經計算，①～⑧號柱間板多垂直桿元模型參數見表1。

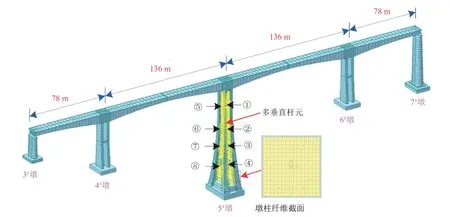
圖6 有限元模型

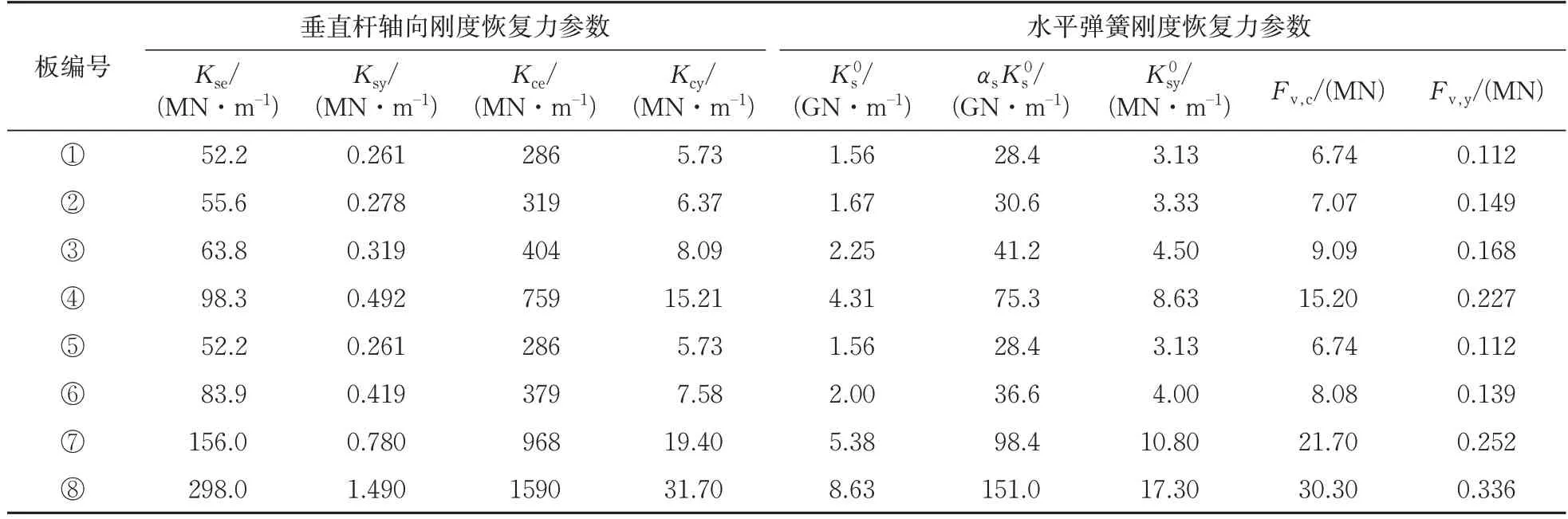
表1 柱間板多垂直桿元模型參數

2.3 模型可靠性驗證

分層殼單元模型具有較高的模擬精度，能夠較準確地反映柱間板平面內、外的彎曲和剪切受力性能［18］。為了驗證本文提出的采用多垂直桿元模型模擬柱間板的新型柱-板組合式高墩模擬方法的可靠性，運用Ritz向量法對本文全橋有限元模型進行自振特性分析。并與同樣運用Ritz向量法的柱間板采用修正二元件模型、分層殼單元模型的結構整體模型振型分析結果進行對比，見表2。由表2可知：本文模型模擬計算結果與分層殼單元模型前5階振型特征一致，2種方法所得各階振型周期最大相對誤差僅為6.1%，驗證了本文模擬方法的可靠性。相較而言，分層殼單元模型計算精度高，但計算耗時較多；二元件模型計算效率較高，但對彎曲彈簧的模擬精度不夠導致計算結果可靠性不高；而本文模擬方法兼具良好的精算精度和計算效率，為該類新型空心高墩的抗震設計有限元建模提供了新思路。

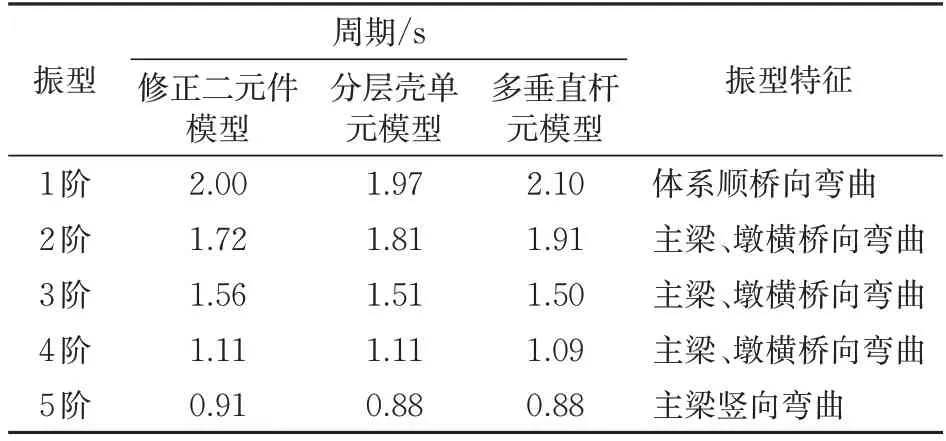
表2 自振特性對比

3 地震易損性分析

3.1 地震易損性

地震易損性［19-20］指結構在地震作用下易發生破壞的性能，可用結構在地震作用下發生不同程度損傷的超越概率評價結構的破壞情況。單個構件的地震損傷超越概率Pf由下式表示。

式中：μd為結構地震需求，μc為結構抗震能力。

根據Cornell 提出的冪運算定律［17］，將地震強度參數PGA與結構響應對數化后進行回歸分析，得到結構地震需求概率函數，即

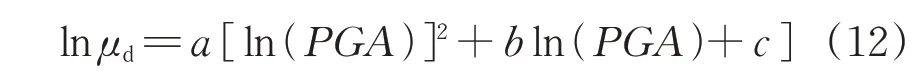
式中：a，b和c均為二次回歸擬合系數。

最后，將式（12）轉換為標準正態分布形式，即

式中：Φ(·)為標準正態分布函數；βc為抗震能力的方差；βd為地震需求的方差。

參考HAZUS99［21］的經驗，PGA作為地震動強度參數時，可取0.5。

3.2 墩柱關鍵位置和柱間板損傷狀態劃分

采用增量動力分析（IDA）方法對縱目溝大橋進行非線性地震響應分析，探究該類新型高墩的地震響應特征，并通過繪制墩柱關鍵截面和柱間板關鍵位置的地震易損性曲線，分析柱-板組合式高墩在不同強度水平地震作用下的損傷超越概率。

對該新型高墩進行地震易損性分析時，柱的關鍵截面選在第1 層柱頂（A-A 截面）、第1 層柱底（B-B截面）、第2層柱底（C-C截面）、第3層柱底（D-D 截面）和第4層柱底（E-E 截面）；柱間板選各層板，如圖7所示。

圖7 橋墩關鍵位置示意圖

合理確定損傷指標是橋梁地震易損性分析的關鍵。本文根據柱-板組合式空心高墩的受力特點，選取墩柱關鍵截面曲率延性比為墩柱損傷指標，選取層間位移角作為柱間板損傷指標。

根據HAZUS99 將墩柱和柱間板的損傷等級劃分為基本完好、輕微破壞、中等破壞、嚴重破壞和完全破壞5個等級。運用X-TRACT 軟件對主墩墩柱關鍵截面進行彎矩-曲率分析，得到對應的首次屈服曲率、等效屈服曲率?y、混凝土壓應變為0.004時的曲率?c4和極限曲率?cmax，作為輕微、中等、嚴重和完全破壞狀態的損傷界限值。并綜合HAZUS99、何浩祥等［22］研究成果，以最大層間位移角作為柱間板各級損傷界限值。經計算，墩柱關鍵截面和柱間板關鍵位置損傷狀態劃分界限值 見表3。

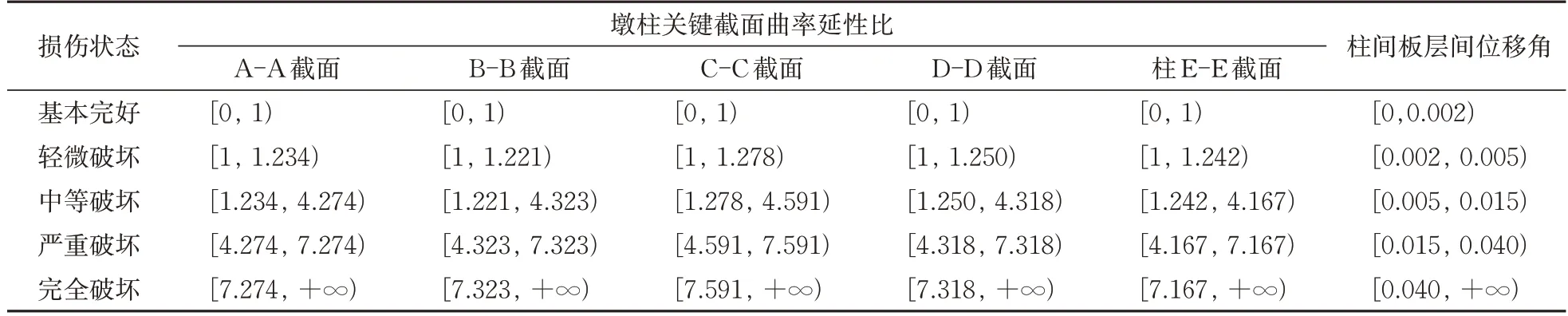
表3 墩柱和柱間板損傷狀態劃分

3.3 地震易損性分析結果

橋址抗震設防烈度為Ⅶ度，地面峰值加速度PGA 為0.109g，反應譜特征周期為0.51 s，參照《黃-韓-侯鐵路陜西段安評報告》，以場地設計反應譜為目標譜，從PEER 選取15條地震記錄，如圖8所示，并以0.05g為步長將所選地震記錄從0～1.0g進行調幅后進行IDA分析。

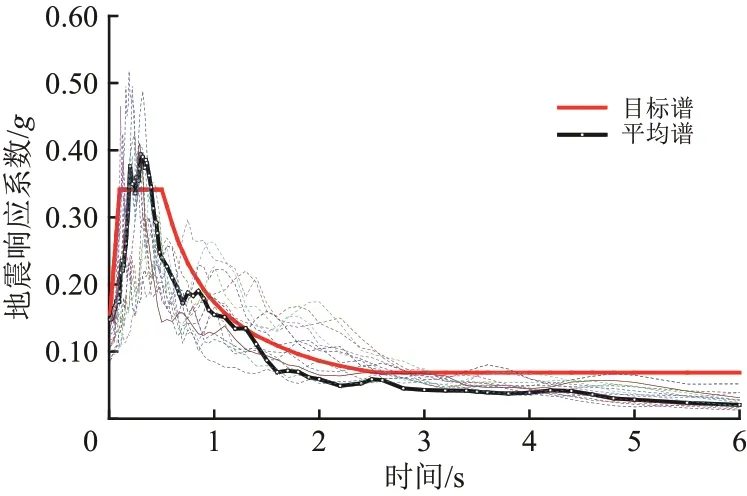
圖8 地震動頻譜

通過IDA 方法對該橋進行非線性地震響應分析，依式（12），根據最小二乘法，對墩柱關鍵截面曲率延性、柱間板層間位移角的計算結果進行二次函數回歸，結果見表4。

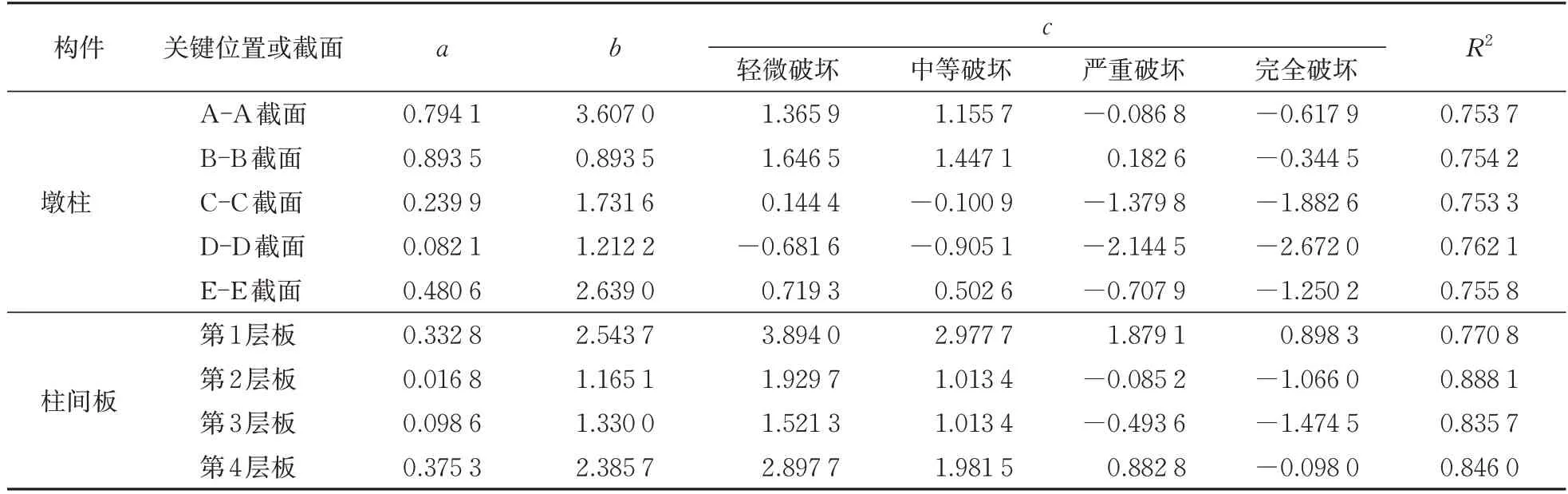
表4 關鍵位置地震需求響應回歸系數

由表4 可知：各關鍵部位地震響應的擬合優度R2值均大于0.75，可見采用二次函數對墩柱和柱間板關鍵截面地震響應的擬合精度較好。將擬合系數代入式（13）即可得到墩柱、柱間板各關鍵位置在不同損傷狀態的超越概率。

以PGA為自變量，通過式（13）計算并繪制該高墩柱間板關鍵位置和墩柱關鍵截面的地震易損性曲線，如圖9和圖10所示。

由圖9可知：

圖9 柱間板地震易損性曲線

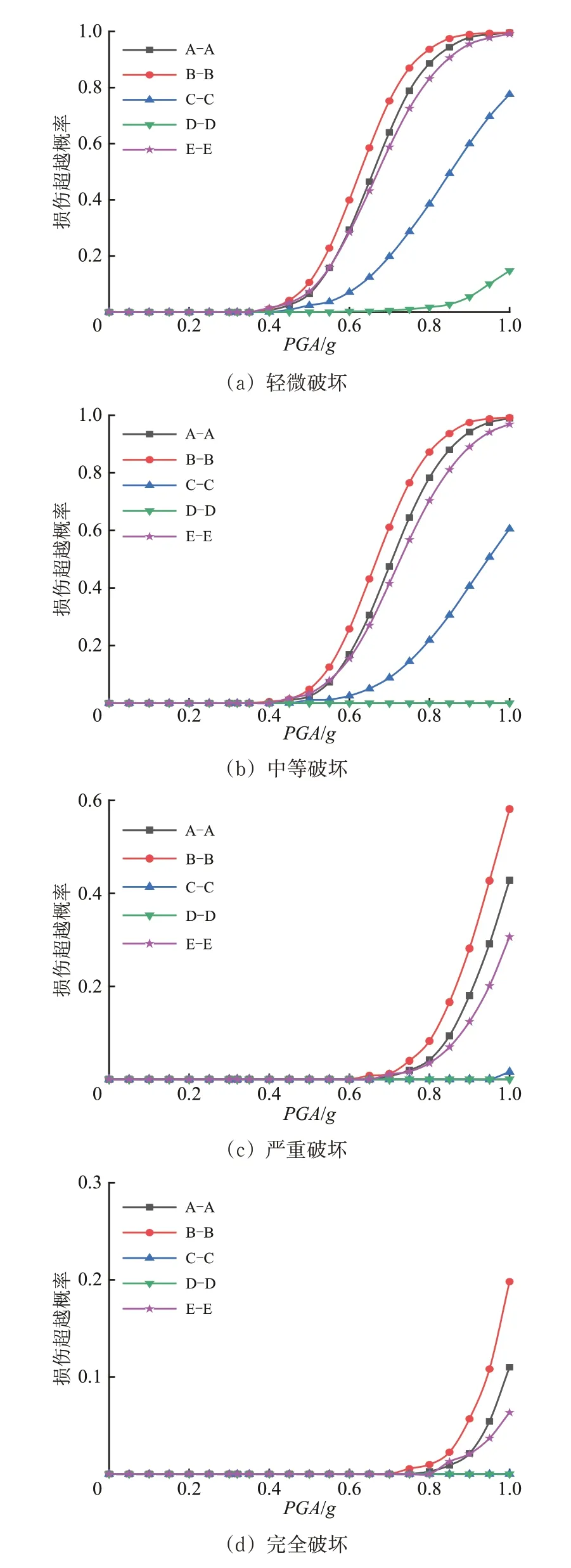
圖10 墩柱地震易損性曲線

（1）在設計地震（0.109g）作用下，柱間板從上至下各層板發生輕微破壞的概率分別為35.2%，9.2%，2.1%和11.3%，發生中等、嚴重及完全破壞的概率均小于3%。

（2）罕遇地震（0.21g）作用下，柱間板從上至下各層板發生輕微破壞的概率分別為93.3%，62.1%，26.4%和57%，發生中等損傷的概率分別為36%，6%，0.7%和5%。

（3）極罕遇地震（0.32g）作用下，柱間板從上至下各層板發生輕微破壞的概率分別為100%，89.2%，60.9%和90.6%，發生中等破壞的概率分別為84.8%，28.3%，6.2%和31.1%，第1 層板最易損，發生嚴重破壞的概率為12%。

（4）同一強度地震作用下，第1 層和第4 層柱間板先于中部板件進入開裂破壞耗能狀態。總體來看，柱間板的損傷概率為第1 層板＞第4 層板＞第2層板＞第3層板。

由圖10可知：

（1）墩柱關鍵部位的損傷超越概率均隨PGA增大而增大，在設計地震、罕遇地震和極罕遇地震作用下，墩柱發生輕微破壞的概率均小于50%，表明墩柱在強震作用下強健性良好。

（2）在相同強度地震作用下，各關鍵截面發生各級損傷的概率均表現為B-B 截面＞A-A 截面＞E-E 截面＞C-C 截面＞D-D 截面，表明該高墩頂層和底層位置較墩中部更易損。

對比圖9和圖10，在相同強度地震作用下，同層上柱間板均先于墩柱發生損傷，這是由于在遭遇地震時，該高墩通過柱間板的損傷消耗地震能量，從而減輕墩柱的損傷程度；當柱間板發生嚴重損傷而逐漸退出工作時，結構整體剛度減小、周期延長，進一步減輕了墩柱發生嚴重損傷的概率，保證了結構整體在強震作用下的強健性。

4 結論

（1）采用多垂直桿元模型模擬柱間板、纖維梁單元模擬墩柱及墩上橫梁的新型柱-板組合式高墩有限元模擬方法兼具良好的計算精度和效率，為該類新型空心高墩的抗震設計有限元建模提供了新思路。

（2）新型柱-板組合式空心高墩在設計、罕遇和極罕遇地震下抗震性能良好，柱間板和墩柱沿墩高方向破壞順序一致，均表現為先頂層、再底層，然后中間層發生損傷。

（3）新型柱-板組合式空心高墩在罕遇地震作用下柱間板發生輕微破壞和中等破壞的概率分別為93.3%和62.1%，而墩柱基本不損傷。該墩通過柱間板優先損傷耗散地震能量，有效減輕了墩柱的損傷程度；當柱間板發生嚴重損傷逐漸退出工作時，結構整體剛度減小、周期延長，有效抑制墩柱發生嚴重損傷，保證了強震作用下全橋結構的強健性。